Правила, приведенные в предыдущих параграфах, помогают легко делить дроби на заданные величины. Если преобразовать эти значения в типичные дроби и разделить их, то энергия будет аналогична распространению 1000, 100 и 10 (обратное верно для дробных долей).
Памятка по действиям с десятичными дробями тренажёр по математике (4 класс) на тему
1) Размножение на 10, 100, 1000 и т.д. (деление на 0,1, 0,01, 0,001 и т.д.) — партия движется вправо, 1, 2, 3 и т.д. Синус.
6.4-1000 = 6,400-1000 = 6400
(2) Разделить на 10, 100, 1000 и т.д. (Умножить на 0.1, 0.01, 0.001 и т.д.) — Сторона перемещается влево, 1, 2, 3 и т.д. Синус.
2.4: 1000 = 0002.4: 1000 = 0.00 24
ii. Десятичное умножение.
Алгоритм 1) Выполните умножение, не обращая внимания на стороны. 2) Вычислите количество десятичных цифр в обоих множителях. 3) Отделите запятые от правой части ответа таким же количеством цифр.
iii.Десятичное деление.
1) Разделите дробь на число, не обращая внимания на стороны. 2) При делении целого числа напишите стороны делителя. 3) Если целое число меньше делителя, поставьте на делителе нулевое целое число. 2. алгоритм деления десятичных дробей. 1) С делителями и делимыми переместите сторону вправо на то же количество цифр, что и после стороны делителя. 2) Деление на натуральные числа. 12 096:2,24 (2 цифры) = 1209,6:224 = 5,4 0,0456:3,8 (1 цифра) = 0,456:38 = 0,012 3:0,75 (2 цифры) = 3,00:0,75 = 300:75 = 4
Умножение десятичных дробей выполняется в три этапа.
- Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
- Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
- В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.
Как умножать десятичные числа
- Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311, а 0,01 как 1.
- Получили 311. Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй — два. Общее количество цифр после запятых: 2 + 2 = 4
- Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.
Добавьте ноль слева, когда число пропущено.
При умножении десятичной дроби на 10, 100, 1000 и т.д. десятичная сторона перемещается вправо как ноль один за другим.
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001 и т.д., эта дробь перемещает десятичную точку влево на столько нулей перед единицей.
При делении десятичных дробей вы можете столкнуться с несколькими случаями
Деление десятичных дробей на натуральные числа
При делении десятичных дробей на натуральные числа действуют следующие правила
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Если целая часть делителя меньше делимого, то коэффициент равен нулю.
Обратите внимание, что неповрежденная часть дроби (здесь 0) меньше делителя (31). Поэтому целая часть дроби равна 0.
По теме: методические разработки, презентации и конспекты
Десятичные дроби. Сравнение и функции десятичных дробей.
Презентация позволяет учащимся повторить тему «Дроби». Их презентация позволяет им повторять тему «дроби», контролировать и принимать свои знания по предмету. И все это — в игровой и доступной форме, позволяет ребенку
Математическая разминка — УП «Числовые операции с числами» и «Дроби».
Цель: развитие математических навыков.
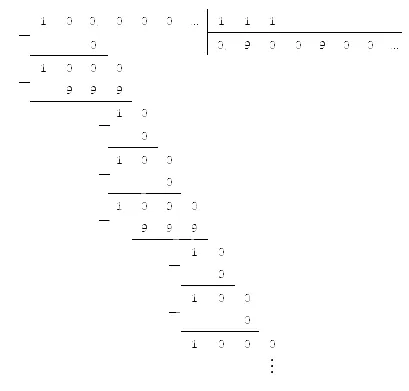
Десятичное деление.
Этот курс построен на использовании AMO. Выбор методов помог функционально скоординировать взаимодействие между учителем и учениками. В курсе использовались учебные состояния. Это способствовало реализации.
Сложение и удаление десятичных чисел.
Этот материал очень полезен.

Распространение десятичных чисел.
Модель планирования курса математики в 5 классе.

Блокноты: «Пункты действий».
Вкладки можно использовать как листовки, помогающие детям изучать предмет в начальной школе.

Блокноты: «Пункты действий».
Вкладки можно использовать как листовки, помогающие детям изучать материал по математической энергии в начальной школе.
В первом примере в делителе два десятичных знака, поэтому мы сдвигаем корпус делителя и сторону делителя вправо на две цифры. Теперь нам остается только разделить цифры.
Как делить десятичную дробь на целое число?
Целые числа — это натуральные числа, их противоположности и нули (… -2, -1, 0, 1, 2 …) являются. По определению целого числа легко догадаться, что алгоритм деления в целом напоминает алгоритм, делящий натуральные числа на дробные доли. Итак.
- Производим вычисления аналогично натуральным числам;
- В случае если присутствует знак следуем следующим правилам:
- Минус разделить на минус получится плюс;
- Минус разделить на плюс получится минус;
- Плюс разделить на минус получится минус.
- В ответе ставим нужный знак.
Пример 4: Разделите 100 на -2,5.
Следуйте алгоритму и выполните вычисления для деления натурального числа на дробь десятичной дроби, не обращая внимания на символ (чтобы избежать путаницы, символ нельзя писать).

Поскольку правило указывает, что СО делится на минус
Деление двух десятичных дробей
деление двух десятичных чисел сводится к предыдущему алгоритму. Это означает, что стороны должны быть удалены. Если в дивиденде еще больше десятичных знаков, чем в делителе, то к дивиденду добавляется соответствующее количество нулей.
Пример 5: Разделите 12,6 на 1,12.
К делителю (12,6) необходимо добавить нули, так как делитель (1,12) имеет два места после десятичной точки для удаления сторон.

Деление десятичных дробей на 10, 100, 1000
Правила деления после запятой на 10, 100, 1000 и т.д. Чтобы получить ответ, нужно перенести влево после делителя столько цифр, сколько нулей в делителе.
Правила деления десятичных чисел на 0,001, 0,01, 0,1 и т.д. Получение ответа заключается в том, что стороны должны сдвинуться вправо к этой дроби на столько, сколько ноль делителя перед делимым.
Чтобы умножить десятичную дробь на другое число, нужно умножить их как целое число, игнорировать сторону и разделить столько десятичных дробей, сколько у вас есть, на два пеликана в полученном произведении.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к разделению в этом случае практически аналогичен. Конечные фрагменты и периодические дроби меняются на обычные дроби, а бесконечные ациклические дроби поворачиваются. Во-первых, возьмем пример натуральных чисел и десятичных дробей.
Преобразуйте 2 и 5 в обычные дроби: 255 10 = 51 2. Далее нам нужно разделить на натуральные числа. Мы уже знаем, как это сделать:.
25, 5:45 = 51 2:45 = 51 2-1 45 = 17 30
Переводя результат в десятичную символику, имеем 0, 5 (6).
Ответ: 25, 5: 45 = 0, 5 (6).
Как разделить десятичную дробь на натуральное число столбиком
Метод разбиения на столбцы подходит не только для натуральных чисел. По аналогии его можно использовать для дробей. Последовательность выполнения функций определяется следующим образом.
Чтобы разделить дробь на натуральное число, необходимо.
1. добавьте несколько нулей к правой десятичной дроби (вы можете добавить любое число, необходимое для деления).
2.Используйте алгоритм для деления дробной части на натуральное число. Когда деление целой части дроби дойдет до конца, поставьте на получившуюся дробь сторону и отмерьте вверх.
Результатом такого деления может быть конечный процент или неопытная периодическая десятичная точка. Это зависит от остатка. Если ноль, то результат будет конечным; если остаток начинает повторяться, то ответом будет циклическая дробь.
Давайте возьмем в качестве примера несколько задач и выполним эти действия с конкретными числами.
Вычислите, сколько будет 65, 14 4.
Используйте метод колонн. Добавьте к дроби два нуля и получите десятичную дробь 65, 1400, которая равна исходной дроби. Затем напишите столбиком и разделите на 4.
Полученное значение является результатом деления целой части. Попросите партию разделить его и двигаться дальше: в
Процесс деления завершается, когда остатки достигают нуля.
При делении этих чисел на угол получается 105 целых чисел. Теперь в делителе не хватает цифры, но вы можете добавить запятую, за которой следует необходимое количество нулей. Каждый раз добавляйте ноль. Вы увидите, что съели 105,5 г сладостей.
Десятичное деление.

Этот видеоурок посвящен делению десятичных чисел. В этом уроке вы узнаете, как разделить десятичное число на другое десятичное число. Вы также узнаете, как делить десятичные числа на натуральные числа, такие как 10, 100 и 1000.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому набору и другим видеоурокам, необходимо приобрести их в каталоге и добавить в личный кабинет.



Конспект урока «Деление десятичных дробей»
-Саш, привет. Что вы готовитесь делать? Может быть, прогуляться на свежем воздухе?
-Здравствуй, Паша. Давай выйдем на улицу, но сначала помоги мне решить одну проблему.
-Мама купила коробку конфет весом 422 грамма. Вся семья съела его за ужином. Каждый из нас получил по пять конфет. Но вдруг я задал вопрос: сколько граммов конфет получил каждый из нас?
Видите ли, нас четверо: я, моя мать, сестра и отец. Конфета весит 422 грамма. Мы пытаемся разделить 422 на 4, но не можем разделить на 4. Но поскольку мы распределяем все конфеты поровну, веса должны быть разделены, а не уравновешены.

-Да, интересно, как это работает. Если вы пойдете к Электроше домой, я уверен, он вам все объяснит.
-Новый вызов. Мы точно знаем, на что делить, но мы не можем разделить 422 на 4. Можете ли вы объяснить, как это делится?
-Конечно, я сейчас все объясню, но сначала давайте решим несколько задач устно.

Прежде чем решить задачу, давайте поговорим о десятичном делении.
Сначала давайте вспомним, как понять запись
-Это значит найти число c при умножении на a.

Те же правила применяются, когда одно из чисел является десятичной дробью.
Например, разделите 1,6 на 2. Получится 0,8. Это объясняется тем, что умножение 0,8 на 2 дает 1,6.
Или, например, разделите 1 на 2, чтобы получить 0,5. Это происходит потому, что умножение 0,5 на 2 дает 1.
Однако не всегда можно найти коэффициент устно.
Например, разделите 39,68 на 16.

-О, Электроша, мы можем сделать эту часть? Мы, конечно, не можем сделать это устно.
-Конечно, мальчики, мы можем разделить эти числа.
Умножим делитель на 100 — вместо десятичной дроби получится натуральное число 3968.
В таком случае коэффициент натурального числа в 100 раз больше искомого.
Разделите эти числа на угол и возьмите число 248. Разделив это число на 100, мы получим искомый коэффициент 2,48.
Давайте проверим правильность нашего деления. Умножьте 2,48 на 16; мы получим 39,68.

Теперь давайте разделим то же самое число другим способом. Не обращая внимания на партию, давайте разделим число на угол. В этот момент вычтите первый десятичный знак. Для этого поставьте запятую перед коэффициентом. Продолжайте делить до конца, чтобы получить 2,48.

– Найдите частное чисел
-Разделить по диагонали. Поскольку 4, деленное на 8, не является делимым, разделите 42 на 8, чтобы получить 5. Остаток равен 2. Скачайте 5. Вычтите первую цифру после запятой, поэтому поставьте запятую после числа 5. Продолжая деление, мы обнаруживаем, что коэффициент нашего числа равен 5,32.
Метод разбиения на столбцы подходит не только для натуральных чисел. По аналогии его можно использовать для дробей. Последовательность выполнения функций определяется следующим образом.
Как разделить столбиком одну десятичную дробь на другую
Для этого переместите сторону к делителю и делитель вправо на одинаковое количество цифр. Тогда делитель будет натуральным числом. Затем выполните указанную выше последовательность действий.
1. мы переносим стороны на делитель, а делитель на цифры нужного числа, чтобы получился делитель натурального числа. Если в делителе недостаточно цифр, добавьте нули справа.
2.Далее делим дробь на столбики с полученным натуральным числом.
Пример: разделите 63,42 на 2,1 в столбик.
Переместите сторону вправо так, чтобы делитель (2.1) был натуральным числом. Переместите сторону к обоим числам — получится 634,2, деленное на 21.

Как разделить десятичные дроби на 1000, 100, 10 и другие
Как вы видите, существуют общие правила деления десятичных дробей. Разделите дробь на десятки, тысячи, тысячные и умножьте на 1/1000, 1/100, 1/10 и т.д.
Для выполнения функции просто переместите влево сторону с нужным количеством цифр (равным нулю). Если в числе не хватает цифр, необходимо добавить справа нужное количество нулей.
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
Правила, приведенные в предыдущих параграфах, помогают легко делить дроби на заданные величины. Если преобразовать эти значения в типичные дроби и разделить их, то энергия будет аналогична распространению 1000, 100 и 10 (обратное верно для дробных долей).
Чтобы найти ответы на эти задачи, переместите сторону на одну, две или три цифры вправо (в зависимости от числа, делящегося на число). Если цифр недостаточно, добавьте нули.
Сделайте это в столбцах. Другими словами, запишите сумму следующим образом (помните, что сложение/вычитание десятичных цифр требует, чтобы дробные части находились на одной вертикальной линии): a. Сложите дробные части. b. Сложите дробные части. c. Сложите дробные части. d. Сложите дробные части.
Алгоритм деления обычной дроби на десятичную.
Вам необходимо определить, какая из двух дробей будет уменьшена на другую сумму. Просто потому, что некоторые обычные дроби не вводятся в десятичной форме. Подробно об этом рассказывается здесь. А если вам нужно разделить инверсии — если вам нужно разделить десятичные дроби на обычные дроби, алгоритм аналогичен!
А на моей стороне десятичные числа всегда преобразуются в обычные или смешанные дроби. Но, как правило, не всегда.
Чтобы понять, нам нужен пример!
Пример деления обычной дроби на десятичную.
Предположим, у вас есть дроби 1/6 и 0,5, которые нужно разделить.
С первого взгляда. Первая дробь имеет знаменатель 6 — это всегда оставляет число в периоде, как в числе 3.
Поэтому здесь дробь преобразуется в обычную дробь.
Теперь, когда у нас есть две одинаковые дроби, мы можем приступить к делению. Мы не будем вдаваться в подробности, чтобы объяснить, как делить обычную дробь — об этом подробно рассказано здесь.
Первое, что вы можете сделать, это уменьшить пропорцию 5/10 на 5/10:5/10:5 = 1/2.
Теперь вы можете приступить к делению дробей.
Как мы знаем из правил деления фрагментов, мы обращаем вторую дробь и превращаем деление в умножение.
Здесь мы видим, что снова можем сократить две дроби, причем 2 — это знаменатель первой дроби и числитель второй.
Вторая дробь, полученная в результате сокращения, равна 1/1, поэтому если мы умножим первую дробь на 1, значение останется прежним. Таким образом, мы имеем 1/3.
В следующем примере деления обычного процента на дробь рассмотрим две дроби 1/4 и 0,5.
В этом случае дробные дроби могут быть преобразованы в обычные дроби, но обычные дроби также могут быть преобразованы в дробные.
Получив две десятичные дроби, их можно разделить на калькуляторы или столбцы двумя способами.
В обоих случаях получены схожие результаты.