Внимание! Если преподаватель обнаружит плагиат в вашей работе, у вас будут большие неприятности (вплоть дочислениЕсли вы не можете написать его самостоятельно, закажите его здесь.
Вещественные числа в математике с примерами решения и образцами выполнения
Вещественные или действительные числа — это математическая абстракция, используемая для представления и сравнения значений физических величин. В основном это такое число Представляется как описание положения точки или линии. Множество вещественных чисел обозначается буквой R и часто называется вещественной линией.
Понятие множества является одним из основных понятий математики. Он относится к к так Они называются первичными, неопределенными понятиями. Слова «набор», «семейство», «система», «комплект» и т.д. являются синонимами слова «Набор». Примерами множеств являются множество учеников в определенном классе, множество студентов, сдавших вступительный экзамен без «тройки», семейство звезд Большой Медведицы, система трех уравнений с тремя неизвестными, множество всех целых чисел и т.д. Приведенные выше примеры показывают, что множество может содержать конечное или бесконечное число целых чисел, и что оно может быть множеством конечных или бесконечных чисел. число Произвольные объекты.
Объекты, составляющие множество, называются его элементами или точками. Наборы часто обозначаются прописными буквами, а их элементы — строчными. Если x является элементом множества X, то пишется (x не принадлежит X). Если — некоторые элементы, то обозначение имеет аналогичный смысл.
Пусть X и Y — два множества. Если X и Y имеют одинаковые элементы, мы говорим, что они согласны, и пишем X=Y. Если X не имеет элементов, не принадлежащих Y, то мы говорим, что X содержится в Y, или что X является подмножеством множества Y. В этом случае мы пишем (Y содержит X). Если X не содержится в Y, то пустое множество является подмножеством любого множества.
Далее мы рассмотрим различные наборы вещественных чисел*. Хотя это может не привести к неточностям, фактическая числа просто называется числами.
* Вместо термина «реальный числа»термин».действительные числа».
Пусть P (x) — это свойство числа х. Тогда обозначение означает множество всех таких числа, обладающие свойством P(x), например, множество корней уравнения с двумя элементами, т.е. пустое множество.
Если
В математических предложениях (формулировках определений, теорем и т.д.) часто повторяются отдельные слова и целые выражения. Поэтому при их записи полезно использовать простые логические символы.
Здесь приведены только некоторые из самых простых и распространенных логических символов. Вместо слова «существует» или «есть» используется обратный латинский символ A (от английского слова any). Символизм означает, например, «для каждого числа x из множества X», и обозначение «.
Для облегчения понимания и чтения утверждений, написанных с использованием логических символов, все, что относится только к отдельным утверждениям, заключено в скобки. Например, символика читается следующим образом так: «для любого такое, что для всех x, не равных x, удовлетворяющих неравенству.
Символ
Изображение вещественных чисел точками на координатной прямой
Давайте введем некоторые вводные термины. Рассмотрим произвольную линию. Мы можем определить два противоположных направления. Выберите один из них и отметьте его стрелкой на рисунке (рис. 1). Предположим далее, что для измерения длины отрезков выбрана единица измерения. Линия с выбранным направлением называется осью.
Рассмотрим любые две точки L и B на оси. Отрезок с граничными точками L и B называется направленным, если мы определим, какая из точек L и B является началом, а какая — концом отрезка. Мы обозначаем направленный отрезок, который начинается в точке А и заканчивается в точке В, буквой, обозначающей начало отрезка, и буквой, обозначающей конец отрезка. Длина направленного сегмента
Для направленных отрезков, лежащих на оси (или параллельных оси), мы вводим понятие длины направленного отрезка. Размер AB направленного отрезка равен, если направления отрезка и оси равны, и равен, как на рисунке 2,
Обратите внимание, что значения направленного отрезка имеют разные знаки в двух направлениях оси: Если точки A и B совпадают, то значение отрезка направления равно.
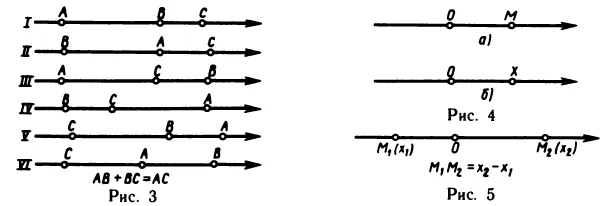
Для любых трех точек A, B и C на оси выполняется равенство AB + BG = AG, которое называется фундаментальным тождеством (используется неоднократно ниже).
Справедливость основного тождества можно легко установить из рисунка, но здесь необходимо рассмотреть несколько случаев относительного положения точек A, B и C на оси. Если все три точки A, B и C различны, то таких есть шесть случаев (рис. 3), в которых базовая идентичность проверяется элементарно.
Давайте теперь обратимся к геометрическому представлению действительных чисел. Рассмотрим линию. Выберите на ней направление (тогда она станет осью) и точку O (начало координат). Линия с выбранным направлением и началом координат называется координатной линией (при условии, что выбрана единица масштабирования). Пусть M — любая точка на прямой (рис. 4, a).
Давайте перейдем к делу М число в точке х, равна значению ОМ направленной прямой с координатой точки М. Таким образом, каждая точка на координатной прямой имеет определенную действительную число — свою координату. Обратное также верно: для каждого реального числу x соответствует точке на координатной прямой, т.е. такая точка M, координата которой равна x.
Это означает, что реальный числа могут быть представлены точками на координатной прямой. По этой причине точка на координатной прямой часто задается в окрестности число -координата (рис. 4, б).
Точка, и точка направленного отрезка, из которого эта формула часто используется в аналитической геометрии.
Некоторые наиболее употребительные числовые множества

Пусть а и b — два числа, и обозначим через athe множество всех действительных чисел. так:
Все эти множества называются интервалами, где a, b — отрезки, а интервалы — пространства. Интервалы конечны; a и b называются их краями. Оставшиеся интервалы называются бесконечными.
Грани числовых множеств
Множество X называется ограниченным сверху (снизу), если существует число с такое, которая в этом случае для каждого числа c называется верхней (нижней) границей X.
Множество, которое одновременно имеет верхнюю и нижнюю границы, называется ограниченным.
Например, каждый конечный вакуум — это множество, которое ограничено вниз, но не ограничено вверх; и вся числовая прямая
Очевидно, что каждое конечное множество X имеет бесконечно много верхних (нижних) ребер. Действительно, если число c является восходящим (нисходящим) ограниченным краем множества X, то каждый число c’, который больше (меньше), чем числа с, — также является верхней (нижней) границей множества X, так справедливостью неравенства
Естественно возникает вопрос о существовании наименьшей из верхних граней множества, ограниченного сверху, и наибольшей из нижних граней множества, ограниченного снизу.
Наименьшая верхняя граница множества X называется точной верхней границей множества X и обозначается sup X, а наибольшая нижняя граница множества X называется точной нижней границей множества и обозначается inf X *.
Примеры:
Пусть α — одно из верхних ребер, а в том числе не имеет точной верхней границы.
Точная верхняя грань (sup X) обладает следующим важным свойством. Не имеет значения, насколько мал число такое, что было бы также верхней границей множества X является и тогда число sup X не будет точной (т.е. наименьшей) верхней границей. Другими словами, это свойство выражает тот факт, что что число sup X — наименьшее из чисел, которые ограничивают верхнюю границу множества X и не могут быть уменьшены.
Приведенное выше свойство точной верхней границы можно сформулировать следующим образом: Если c = sup X, то для каждого числа с’ < с существует число Чтобы убедиться в эквивалентности этих формулировок, достаточно взять c' и e ограниченными равенством, которое задается условием
Точная нижняя граница обладает аналогичным свойством — какой бы маленькой она ни была число е>0, найдено (сформулируйте это свойство сами в другой форме).
Возникает вопрос, всегда ли множество, ограниченное сверху (снизу), имеет точную верхнюю (нижнюю) границу. Ответ на этот вопрос дает следующая важная теорема.
Теорема:
Каждое непустое множество, ограниченное верхним (нижним) числовоe множество имеет точные верхние (нижние) ребра.
Доказательство:
Пусть X — непустое множество, ограниченное сверху. Тогда множество Y чисел, ограничивающих X сверху, непусто. Из определения верхней границы следует, что для каждого из неравенств.
Из первого неравенства (1) получаем что число c, которая ограничивает множество X сверху, т.е. является верхней границей, а из второго следует, что она является наименьшей из таких числа, т.е. это точная верхняя граница.
Таким же образом мы рассмотрим случай, когда существует точная нижняя граница непустого ограниченного снизу множества.
Если множество X не ограничено сверху (снизу), то обычно пишут:








