Углы могут быть обозначены разными цветами. Главное, чтобы она была простой и запоминающейся. Не все углы должны быть отмечены. Только те углы, которые необходимы для решения проблемы.
Определение угла
Углы — это простые геометрические фигуры. Определение угла напрямую связано со значением радиуса.
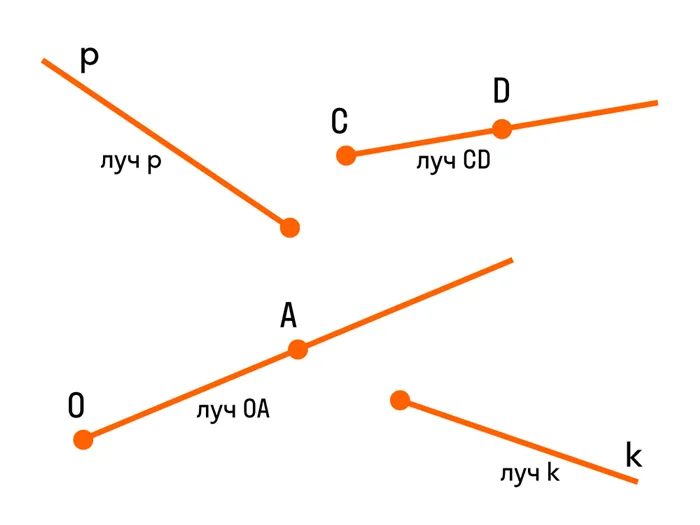
Радиус — это прямая линия, которая имеет начало, но не имеет конца и простирается только в одном направлении.
Если дана прямая A на плоскости и точка o на этой прямой, то она преобразуется в две части. Каждая часть линии представляет собой радиус с началом в точке o.
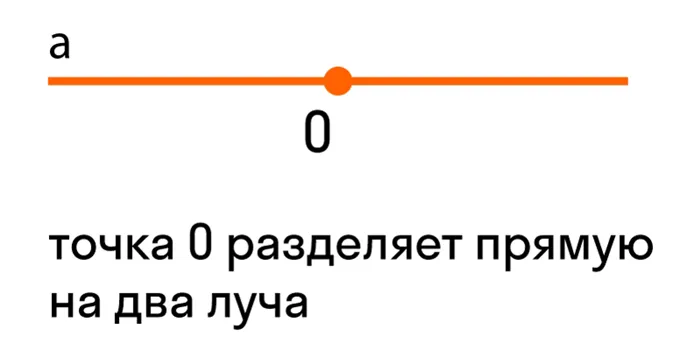
Радиус символизируется буквой латинского алфавита или двумя строчными буквами. Например.
Угол — это часть уровня между двумя прямыми линиями, начинающимися из одной точки. Обе стороны угла являются радиусами, а вершина — общим принципом сторон.
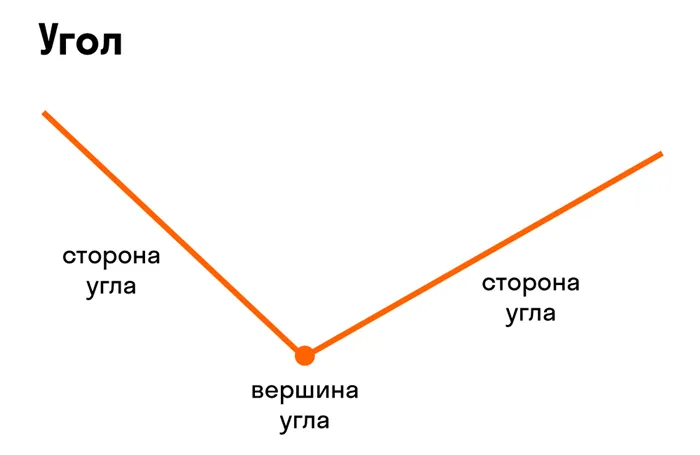
Что такое вершина и стороны угла?
В математике существует специальный символ для обозначения углов — ¶.
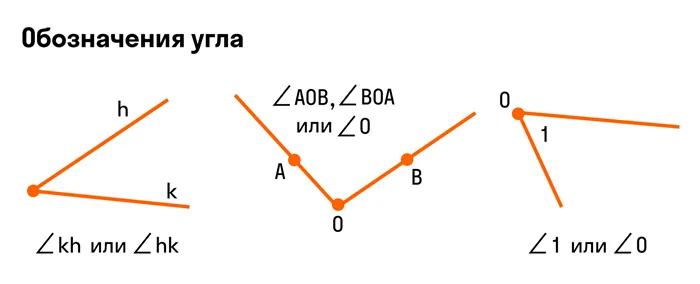
Когда стороны угла называются маленькими латинскими буквами, они пишутся после символа. Например, ∠AB или ∠BA.
Когда стороны угла обозначаются заглавными буквами, символ угла и три буквы составляют угол, при этом вершина всегда пишется посередине. Если стороны угла равны OA и OB, то названия угла записываются как ∠AOB и NOBOA. Вы также можете назвать угол с большой буквы, обозначающей вершину.
Может быть цифровая идентификация — это тоже возможно.
Например, все способы наименования угла:.
Если угол делит уровень на две части, то одна будет внутренней областью угла, а другая — внешней. Например:.
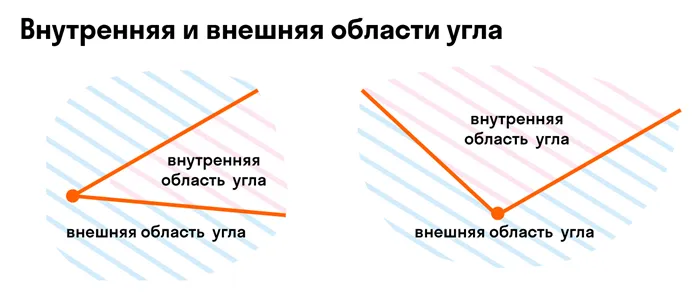
Единицей измерения угла является градус. Символ для обозначения градуса угла: °.
Виды углов
Существует несколько типов углов, и каждый имеет свое название.
В геометрии важно различать типы углов. Это можно сделать на глаз или с помощью линейки.
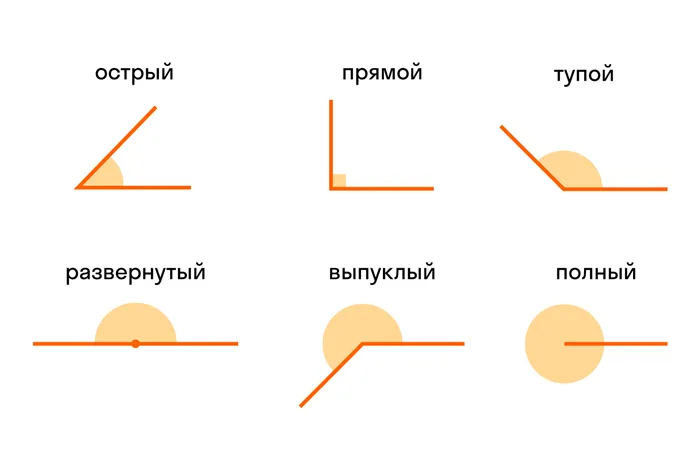
Прямые углы — это углы, стороны которых перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два соседних угла равны между собой, то каждый из них является прямым углом. Для удобства прямые углы символизируются углами. Например, так:.
На изображении показаны два правильных угла Шипл — AOC и NOCOB. Общая сторона OC перпендикулярна прямой AB, а точка O является основанием перпендикуляра.
Острые углы — это прямые углы, т.е. углы с малыми углами.< 90°.
Открытый угол — это открытый угол, образованный двумя лучами света, равный сумме двух правильных углов. Открытый угол равен 180°. Как выглядит разработанный угол, показано на первом рисунке.
Когда развернутый угол делится на плоскости, каждая часть угла считается внутренней областью развернутого угла.
Неравный угол — это любой угол, который не является вычитаемым углом. Другими словами, она не равна 180°.
Тупые углы — это углы, которые больше прямых, но являются углами развития (меньше 90°).< тупой угол < 180°.
Выпуклый угол — это угол, который больше прямого угла, но меньше полного (180°).< выпуклый угол < 360°.
Полные углы — это углы, обе стороны которых имеют одинаковый радиус. Это равно сумме четырех правильных углов, т.е. = 360°.
Смежные углы — это пары углов с общей вершиной и стороной, причем другая сторона находится на противоположной стороне от общей стороны.
На рисунке изображены два смежных угла anob и ∠BOC, с общей вершиной o, общей ob.
Это определение может быть сформулировано по-разному. Если радиус вычитается из вершины угла, делящего угол на два, то образовавшиеся углы являются смежными.
Чтобы разделить угол на радиус, прибавьте угол. Из этого можно выделить следующие корректные различия.
Углы называются прямыми, если они равны 90°, острыми, если они меньше 90°, и тупыми, если они больше 90° и меньше 180°. Открытый угол равен 180°.
Онлайн-школа Skysmart поощряет детей и подростков к занятиям математикой. За интересные задачи, знание новых приложений и хорошие оценки!
Сравнение углов
Для сравнения углов можно использовать метод наложения, который является самым простым методом в учебной программе 4 класса. Для этого сопоставьте две вершины и одну сторону одного угла с одной стороной другого. Если стороны определенного угла совпадают, то углы равны. Если нет, то угол внутри другого угла будет меньше. Ниже приведены два наглядных примера равных и неравных углов.
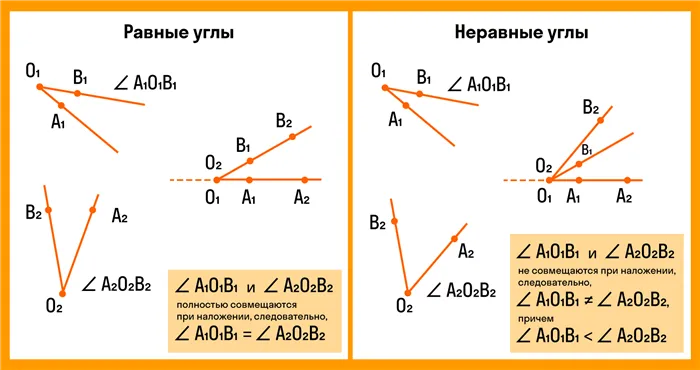
Ракурсы для разработки всегда одни и те же.
Углы ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 расположены следующим образом.
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если другие стороны также совпадают, то углы равны: ∠𝐴𝐵𝐶=∠𝑀𝑁𝐾.
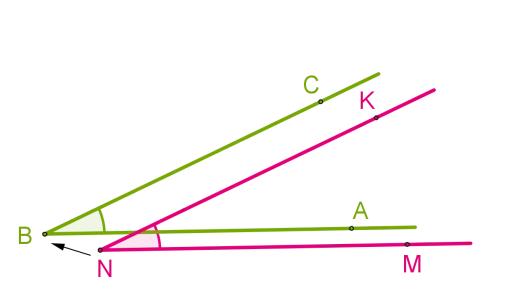
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶
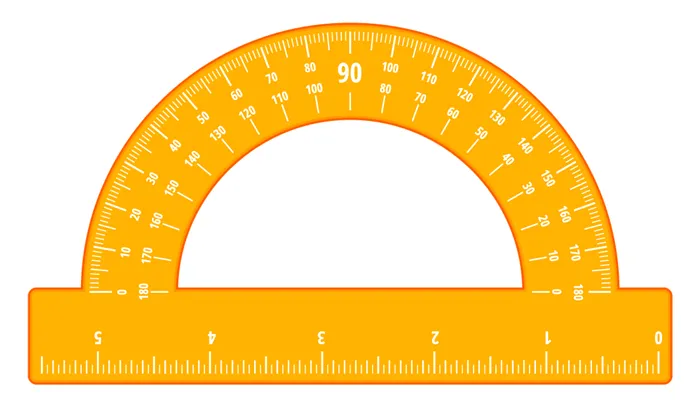
Углы также можно сравнивать, измеряя их значения. Для построения и измерения углов вам понадобится специальный инструмент — транспортир. Вот как это выглядит:.
Чтобы понять взаимосвязь между объектами, изучите отношения между различными частями. Определяя отношения между ними, вы найдете синус, косинус (что это такое?), тангенс (что это такое?), касательную (что это такое?). ), вводятся понятия тангенса и катагонали.
Теорема Пифагора
Теорема основана на утверждении, что в прямоугольном треугольнике сумма квадратов длин перпендикулярных линий равна квадрату длины гипотенузы. В пресс-релизе говорится, что
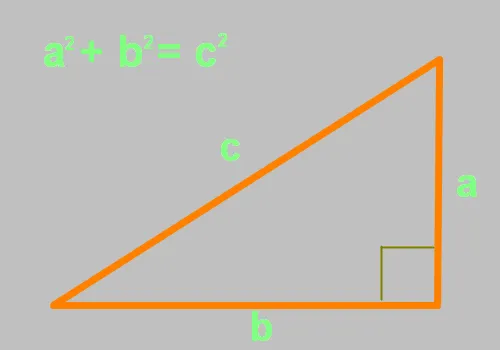
Стороны a и b — катеты, угол между которыми составляет ровно 90 градусов. Таким образом, сторона c является косой. Подставив две известные величины в это уравнение, можно рассчитать третью неизвестную величину. В результате можно регистрировать и контролировать правильный угол.
Теорема Пифагора также известна как «египетский треугольник». Это треугольник со сторонами 3, 4 и 5; единицы длины не имеют значения. Расстояние между сторонами 3 и 4 составляет ровно 90 градусов. Проверим это утверждение с помощью приведенного выше уравнения: a²+b²=c²= (3 x 3) + (4 x 4) = 9 + 16 = (5 x 5) = 25- все сходится!
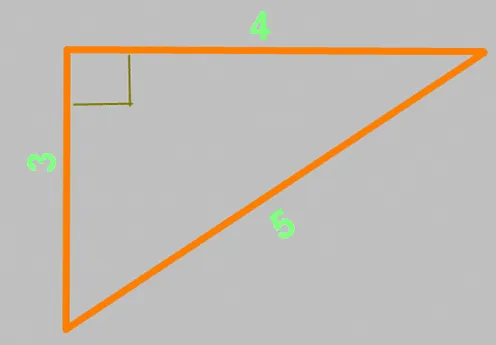
Теперь давайте применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — контроля прямых углов с помощью теоремы Пифагора. Самый распространенный пример в отделке и строительстве — проверка перпендикулярности стен. Вертикальные стены — это стены, расположенные под углом 90° друг к другу.
Возьмите внутренний угол, который вы хотите контролировать. Обратите внимание на длину обеих стен (одинаковой высоты) или пола. Длина этих секций не является обязательной. Если возможно, следует разметить как можно больше, но полезно измерить диагонали между отметками на стенах. Например, отметьте 2,5 метра (или 250 см) на одной стене и 3 метра (или 300 см) на другой. Затем возведите в квадрат длину каждого участка стены (умножьте на себя) и сложите полученное произведение. Результат: (2,5 x 2,5) + (3 x 3) = 15,25 — это квадрат диагонали. Теперь вычтите квадратный корень из этого числа. √15,25 ≈ 3,90 — 3,9 метра — диагональ между точками. Если рулетка показывает разную длину диагонали, то контролируемый угол поворачивается и происходит отклонение на 90°.
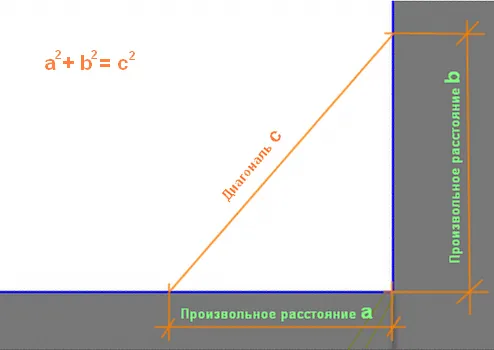
Калькулятор расчета диагонали прямого угла
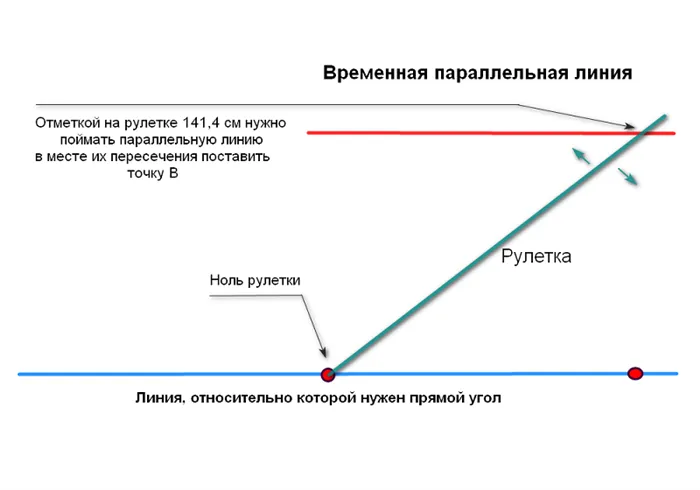
Экспорт квадратных корней мне не понравился — простые люди не могут обойтись без калькуляторов. Не все мобильные расчеты можно экспортировать. Поэтому можно использовать упрощенный метод. Необходимо помнить, что прямой угол ровно 100 см является диагональю 141,4 см. Таким образом, для прямого угла со стороной 2 м. — Диагональ составляет 282,8 см. Это означает, что каждое измерение составляет 141,4 см. У этого метода есть недостатки. На обеих стенах должно быть измерено одинаковое расстояние, и оно должно быть кратно 1 метру. Я не могу сказать наверняка, но в моей скромной практике это гораздо удобнее. Не следует полностью забывать о первоначальном методе, но в некоторых случаях он очень важен.
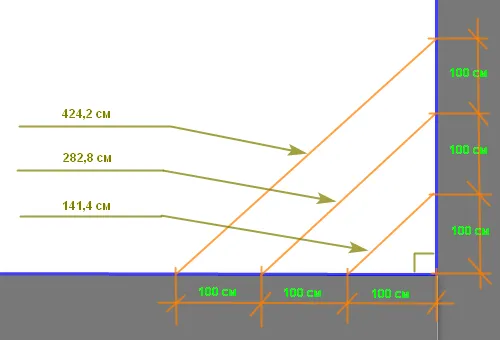
Сразу возникает вопрос: какое отклонение от расчетной длины диагонали считается нормальным (ошибкой), а какое — нет? Если угол, контролируемый отмеченным краем 1 м, составляет 89°, диагональ уменьшается до 140 см. Понимая эту взаимосвязь, можно сделать объективный вывод, что ошибка диагонали 141,4 см в несколько миллиметров не дает расхождения в общей оценке.
Как я могу проверить внешние углы? Наружный контроль в основном такой же, просто проденьте каждую линию стены до пола (или до земли с помощью кабеля) и измерьте внутренние углы обычным способом.
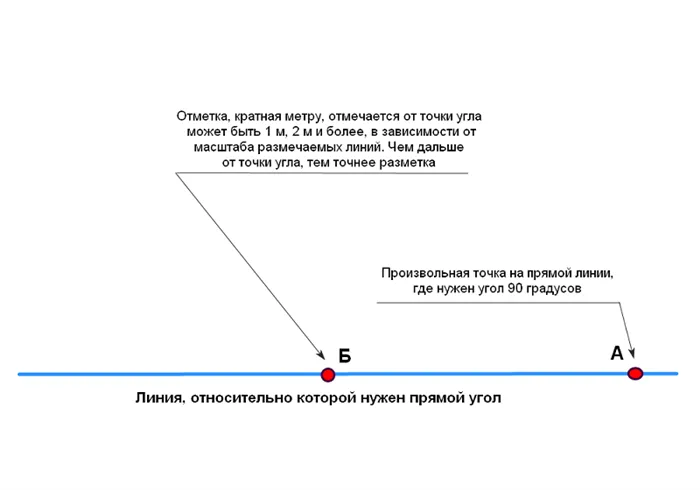
Как разметить прямой угол рулеткой
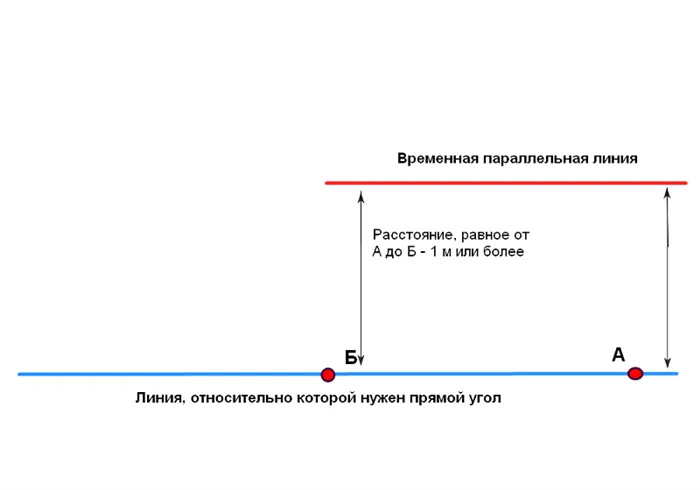
Разметка основана либо на общей теореме Пифагора, либо на началах «египетского треугольника». Однако, хотя теоретически на бумаге проектируются только линии, «поймать» все выбранные размеры с помощью шнуров или линий, протянутых на полу, — более сложная задача.
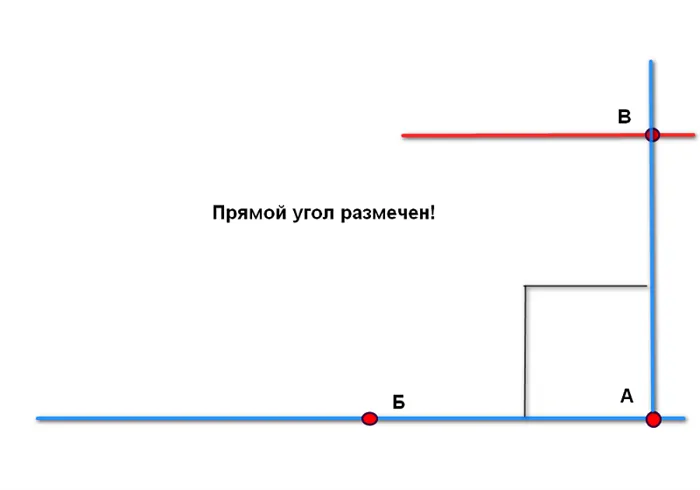
Поэтому рекомендуется упрощенный метод, основанный на диагоналях 141,4 см треугольника со сторонами 100 см. Вся последовательность раскладки показана на следующих рисунках. Важно помнить. Диагональ 141,4 см нужно умножить на количество измерений в секции AB. Отрезки AB и AB должны быть равны и соответствовать целым числам метров. Нажмите на картинку, чтобы увеличить ее!
Значение. Два угла называются перпендикулярными, если сторона одного угла равна дополнительной половине стороны другого угла.
Углы в 30 и 45 градусов
Выбор одного из способов вычисления угла 90° с помощью ленты не затрудняет формирование трех различных острых углов. 45 градусов возникает независимо от того, является ли треугольник равнобедренным или нет. Для 30 градусов подчиненный должен быть вытянут. Это равно двум коротким вертикалям. Здесь угол между ними остается равным 60 градусам.
В этом видео учитель делится своим опытом экспорта прямых углов с помощью теоремы Пифагора и египетского треугольника.

Коротко главном
В помещениях часто необходимо спроектировать прямые углы под мебелью и гидравлическими компонентами.
Существует три способа контроля угла 90° с помощью одной ленты: если соединительная линия между стенами длиной 1 метр равна 141,4 см, то стороны составляют 3/4/5 частей.
Ленты также достаточно для образования трех углов в 30, 45 и 60 градусов.
Кроме того, для выставления оценок могут потребоваться только калькулятор и карандаш.
Угол — это геометрическая фигура, образованная двумя лучами света (сторонами угла), исходящими из одной точки (называемой вершиной угла). Уровень, содержащий обе стороны одного угла, разделен на две зоны.
Градусная мера вписанного угла
Тогда градусная оценка угла регистрации равна половине градусной оценки смычка и половине градусной оценки угла на том же смычке.
Выгравированный угол будет равен 0,5 метра лука на дуге, на которой он расположен.
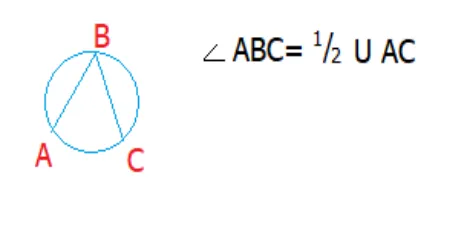
Рисунок 2.
Различают также различные типы углов.
Прямые углы равны 90 градусам. Острые углы меньше 90 градусов. А тупые углы — это углы больше 90 градусов и меньше 180 градусов. Так как же важно уметь считать углы и градусы? Он полезен при проведении следующих исследований Астрономия. Например, вычисление положения различных тел в пространстве. Чтобы попрактиковаться в этом, нужно нарисовать много углов, отличающихся друг от друга. Также важно практиковаться в рисовании. Вы также можете попрактиковаться в построении углов с произвольными числами с помощью транспортира.
Существует также концепция перегородок.
Биссектриса — это радиус, исходящий из вершины этого угла и делящий его посередине.
Пример 1. Разделы и экстенсивные угловые задачи.
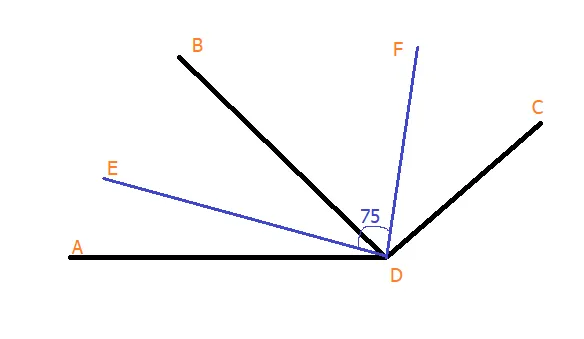
Рисунок 3.
Рис. 3. Лучи DE и DF парализованы, соответствуют углам ADB и BDC.
Найдите угол ADC, угол EDF = 75°.
Ответ. Угол EDF равен половине угла ADB и BDC. Это означает, что EDF составляет половину угла ADC. Теперь угол ADC = 75 умножается на 2 = 150°.
Пример 2. Биссектрисы углов и прямые углы.
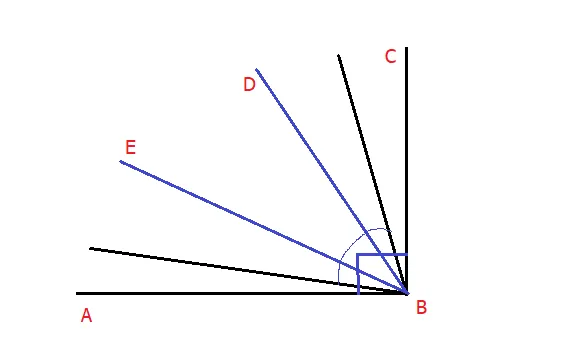
Рисунок 4.
На рисунке 4 видно, что угол ABC является правильным, а угол ABE EBD DBC — равным. Необходимо найти углы, образованные бисекторами ABE и DBC.
Решение: угол ABC правильный и поэтому равен 90°. Угол EBD = 90/3 = 30°. Согласно правилам, углы ABE EBD DBC равны и поэтому каждый из них = 30°. Более того, оказывается, что бисектор любого из трех углов разделит любой из этих углов на два угла, равных 15°. Поскольку оба угла ABE и DBC связаны с найденными углами, можно смело утверждать, что вычисляемый угол равен 30+15+15 = 60°.
Градусная мера углов треугольника
Каждая геометрическая фигура, кроме круглой, имеет угол. Рассматривая углы треугольника, мы видим, что Сумма углов треугольника всегда равна 180°. Рассматривая прямоугольный треугольник, мы видим, что один из углов равен 90°. Сумма двух других углов также равна 90°.
Поэтому, если мы знаем, сколько градусов составляет один из острых углов треугольника, второй угол можно найти по типу.
Два других угла — острые, так как прямоугольные треугольники имеют прямые углы.
Острые углы объясняются следующим образом. Острые углы — это углы менее 90 градусов.
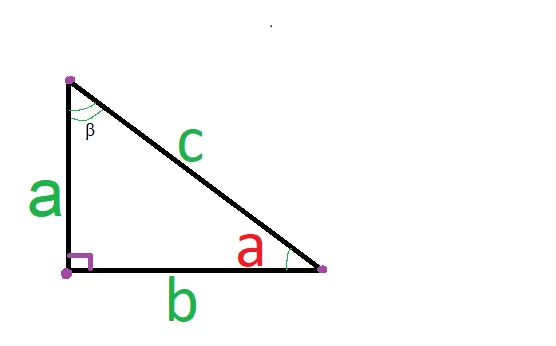
Рисунок 5: Прямоугольный треугольник
Из вышесказанного следует, что прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками. Эти участки связаны с тремя точками. Все их углы — внутренние, один из которых прямой и соответствует 90°. Пример показан на рисунке 5.
2. если два луча света параллельны, но не лежат на одной прямой, начертите уровень, проходящий через принцип и разделяющий пространство на два полудома. Если лучи находятся в одном из этих полудомов, то они находятся под совместным надзором (рис. 2.51). Если лучи света находятся в разных полушариях, они имеют противоположные направления (рис. 2.52).
Смежные углы
Значение. Если два угла имеют одну общую плоскость и противоположные стороны этих углов являются дополнительными полуплоскостями, то такие углы называются смежными.
На рисунке 2.77
Сумма смежных углов равна 180°.
Следующий результат вытекает из Теоремы 4, т.е. из свойства смежных углов.
Последующее 1. Если два угла равны, то смежные углы равны.
Последующее 2. Угол, касательный к прямому углу, является прямым углом.
Впоследствии 3. Углы, касательные к острым углам, являются тупыми, а углы, касательные к тупым углам, являются острыми.
Вертикальные углы
На рисунке 2.78 изображены две пересекающиеся в точке О прямые АВ и CD. При пересечении этих прямых образовалось четыре угла:
Значение. Два угла называются перпендикулярными, если сторона одного угла равна дополнительной половине стороны другого угла.
На рисунке 2.78 углы 1 и 3, 2 и 4 перпендикулярны.
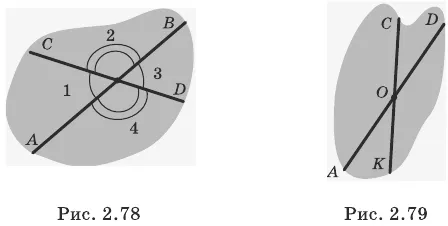
Очевидно, что две пересекающиеся прямые образуют смежный вертикальный угол и перпендикулярный угол. Смежные углы дополняют друг друга до 180°. Меньший угол из двух называется углом между линиями.
Пример:
На рисунке 2.79 угол треска равен 30°. Чему равны углы AOC и DOK?
1. прямые CK и AD пересекаются в точке O
2.
4. угол между COD и AOK является вертикальным (1, определение вертикального угла).
5.
6. угол dok содержит угол cod (1, определение тангенса угла).
7.
Эта лекция взята со страницы с полным текстом урока «Математика».
См. также дополнительные лекции по предмету математика.
Отправляйте задания в любое время дня и ночи.
Официальный сайт Брилионо Банаталия Валерий Эвант Профессор Екатеринбургского государственного института.
Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.
Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.
При копировании материалов ссылка на сайт Natalibrilenova.ru обязательна.








