Косая сторона — это противоположная (наибольшая) сторона прямого угла; в треугольнике это сторона AC. Катетеры — это две другие стороны рядом с прямым углом; в треугольнике это BC и AB.
Что такое тангенс угла
Рисунок 1 Графики тригонометрических функций: полутон, косинус, тангенс, вторичная, сопряженная, котангенс и катагональ.
Тригонометрические функции являются одним из видов элементарных функций. К ним обычно относятся синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), sec x) и cosec x, причем последние две функции используются относительно редко (о менее часто используемых функциях см. здесь).. (Функция). В английской литературе касательные, косоугольники и косеканы обозначаются tan x, cot x и cscx. Тригонометрические функции обычно определяются геометрически, но могут быть определены детально через суммы рядов или как решения определенных дифференциальных уравнений. Это позволяет распространить определение этих функций на комплексные числа.
Содержание
Геометрическое определение
Тригонометрические функции обычно определяются геометрически. Пусть будет декартова система координат на плоскости и окружность радиуса R с принципом O в качестве центра. Пусть угол измеряется как поворот от положительного направления горизонтальной оси к лучу OB. Направление против часовой стрелки является положительным, а направление по часовой стрелке — отрицательным. Обозначим через xB и покажем его упорядоченным по yB (см. рис.)
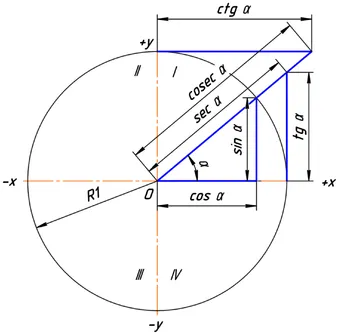
Рис. 3. Тригонометрические функции угла α с радиусом, равным 1.
Благодаря схожим свойствам формы, очевидно, что значение тригонометрической функции не зависит от радиуса окружности R. Во многих случаях этот радиус принимается равным значению единичного отрезка, а синусоида — это просто прямой угол y.B Синус — это отклонение xB. На рисунке 3 показана величина тригонометрической функции единичного круга.
Когда a вещественно, синус a в математическом анализе — это синус угла, радиальное измерение которого равно a, как и для других тригонометрических функций.
Определение тригонометрических функций для острых углов
Во многих предыдущих учебниках по геометрии тригонометрическая функция острого угла определяется как отношение сторон прямоугольного треугольника. Пусть OAB — треугольник с углом a. Итак.
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Постройте систему координат, используя направление ребер линий вдоль начала координат O и OA, при необходимости измените направление (инверсия) треугольника и поместите его в первую четверть системы координат, затем постройте окружность. Для радиуса, равного косой грани, сразу видно, что определение этой функции дает тот же результат, что и предыдущее определение. Это определение имеет ряд педагогических преимуществ, так как не требует введения понятия системы координат, но имеет и серьезный недостаток: нельзя определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении базовых задач. тупоугольные треугольники (см. теорема о полутонах, теорема о коэффициентах).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинуса и полутона можно определить как четные (полутон) и нечетные (синус) решения дифференциальных уравнений.
R(\varphi) = — R(\varphi),» width=»» height=»» />
Если начальное условие cos(0) = sin'(0) = 1, то есть производная второго порядка берется как функция переменной, равной самой функции, со знаком минус.
Определение тригонометрических функций как решений функциональных уравнений
Функции кокерина и синуса можно определить как непрерывные решения (f и g соответственно) системы интересных уравнений: f(x+y)& amp; amp; f(x)f(y)-g(x(x))-g(y)™ g(x+y)& amp; amp; «width =» «height =» » />
Значения тригонометрических функций для некоторых углов
Значения синуса, зм, тангенса, котескида, вторичного и конкретного углов приведены в таблице.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
| \,\!» width=»» height=»» /> | \,\!» width=»» height=»» /> | \,\!» width=»» height=»» /> | ||||||
| \,\!» width=»» height=»» /> | \,\!» width=»» height=»» /> | \,\!» width=»» height=»» /> |
Значения тригонометрических функций нестандартных углов
= \sin 18^\circ = \frac-1>» width=»» height=»» />
= \ оператор 1.5^\ circ = \ sqrt<\frac<8-\sqrt<2(2-\sqrt)(3-\sqrt)> — \ sqrt.< 2(2+\sqrt)(5+\sqrt)>><8+\sqrt<2(2-\sqrt)(3-\sqrt)>+# sqrt<2(2+\sqrt)(5+\sqrt)> >> «ширина =» «» высота =»»
= \ frac left \ sqrt >> \ left(섹 sqrt)<2(5+\sqrt)>+\ sqrt- \ sqrt- \ справа) +\ sqrt >> \ слева (섹 sqrt)<6(5+\sqrt)>+\ sqrt -1 \ right) \ right) «width =» «height =» » />
= \ frac \ sqrt) >> — \ sqrt >> — 4 \ sqrt<2(17+\sqrt)> + 3\sqrt+17>+# sqrt<2(17-\sqrt)>+Ј sqrt+15 \ right) >>» width =»» height =»» />
Вместо «касательная к углу альфа» пишут TGA. Различные названия распространены на калькуляторах и различных компьютерных программах и ПК.
Таблица тангенсов и котангенсов (главных углов от 0° до 360°)
| α градусов | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| α радиан | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| tg α | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctg α | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
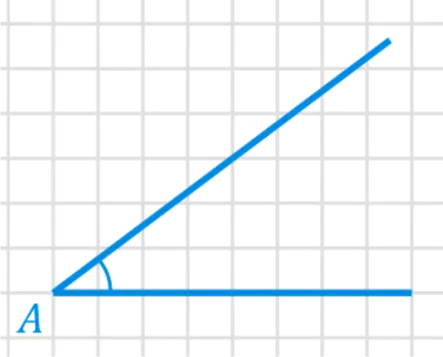
Что такое синус?
Половина угла (sin) — это отношение противоположной ноги (противоположной стороны угла) к подчиненной (максимальной стороне, противоположной углу).
В примере sin a = bc/ac.
Что такое косинус?
Косинус угла (cos) — это отношение прилежащего перпендикуляра (рядом с углом) к подчиненному (наибольшая сторона, противоположная прямому углу). В данном примере cos a = ab/ac.
Угловой тренер (CTG) — это отношение смежных катетов (рядом с углом) к противоположным катетам (напротив угла). В примере CTG A = AB / BC. Заметим, что котоген является «тангенциальной обратной» (смежная обратная делится на противоположную), т.е. CTG a = ab / bc, а tg a = bc / ab (противоположная делится на смежную).
Если начальное условие cos(0) = sin'(0) = 1, то есть производная второго порядка берется как функция переменной, равной самой функции, со знаком минус.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших \(360°\) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Рассчитайте \(tg \:0 \).Решение. Чтобы найти касательную к нулю, сначала нужно найти синус и косинус ⌘(0 \). Вы увидите, что и те, и другие используютсяКруг из треугольников. :.
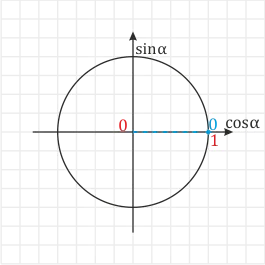
Точка ⌘ (0 \) числовой окружности совпадает с точкой ⌘ (1 \) на оси косинусов, поэтому (cos \: 0 = 1 \). Вычитая перпендикуляр к оси синусов из точки ⌘ (0 \) числового цикла, приходим к точке ⌘ (0 \). Следовательно, ዄ (tg \: 0 = \) ዄ (ዄ frac) ዄ (= \) ዄ (ዄ frac) ዄ (= 0 \).
Пример. \Вычислить \(tg \: (-765^{ circ)}).Решение. \Вычислите синус и косинус \(tg \: (-765^\ circ) = \)\(Lo_765^°F)\(-765^°F)Lo_765^F)Lo_765^F). Спроектируйте \(-765^°\) в треугольном цикле. Для этого нам нужно повернуть в отрицательную сторону на ⌘ (720^°\), затем еще на ⌘ (45^°\).
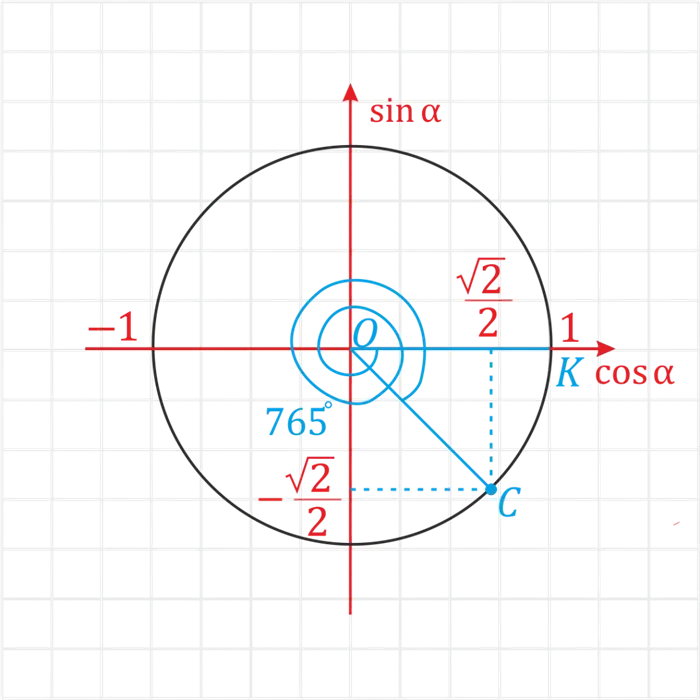
Однако вы также можете определить касательные непосредственно через треугольный цикл, проведя дополнительные оси.
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
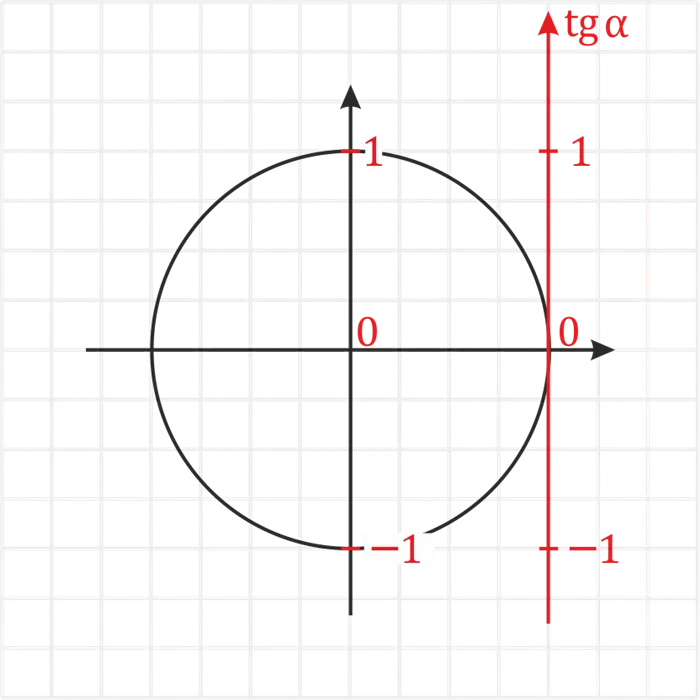
Ось тангенса фактически является копией оси синуса, только со сдвигом. Поэтому все числа в нем располагаются так же, как и на оси синуса.
Чтобы определить тангенс с помощью числовой окружности, нужно: 1) Отметить соответствующую аргументу тангенса точку на числовой окружности. 2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов. 3) Найти координату пересечения этой прямой и оси тангенсов.
Пример. \Вычислите \(tg \:Lo_ frac \).Решение. 1) Окружите себя вниманием ᢙᢙᢙᢙᢙᢙᢙᢙ.
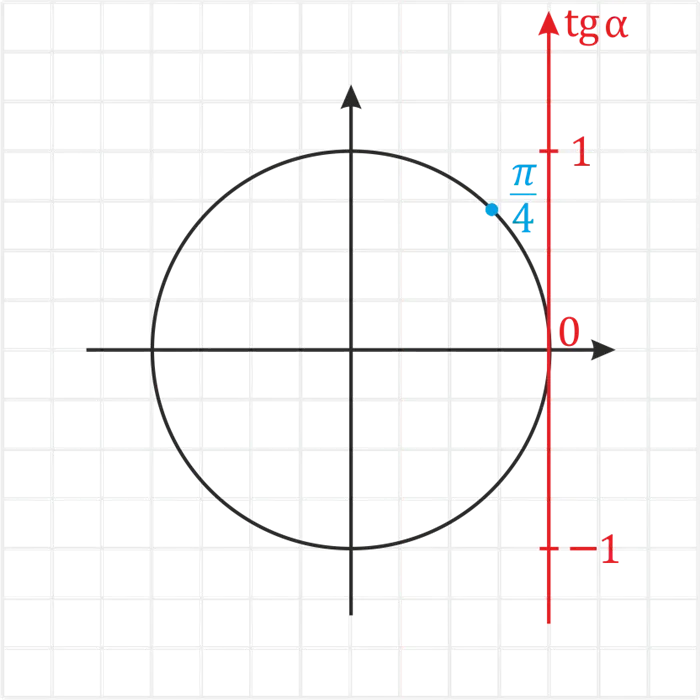
2) Проведите прямую линию через эту точку и авторитет.
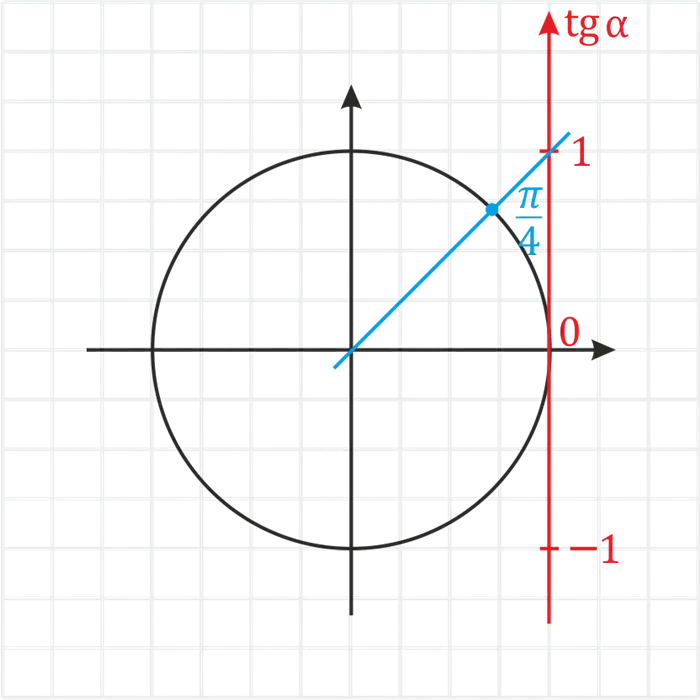
3) В этом случае нет необходимости находить координаты, так как они равны \(1 \).
Пример. \Вычислите \(tg \:45°)™ и Ў(tg \:-240°)Ў.Решение. Для угла ⌘ (45°\) (⌘ (坐地\)) касательная линия будет ⌘ (1 \). Она пересекает касательный вал. А для угла ⌘(-240°\) (⌘(∠KOB\)) касательная линия равна ⌘(- \ sqrt \) (приблизительно ⌘(-1,73 \)).
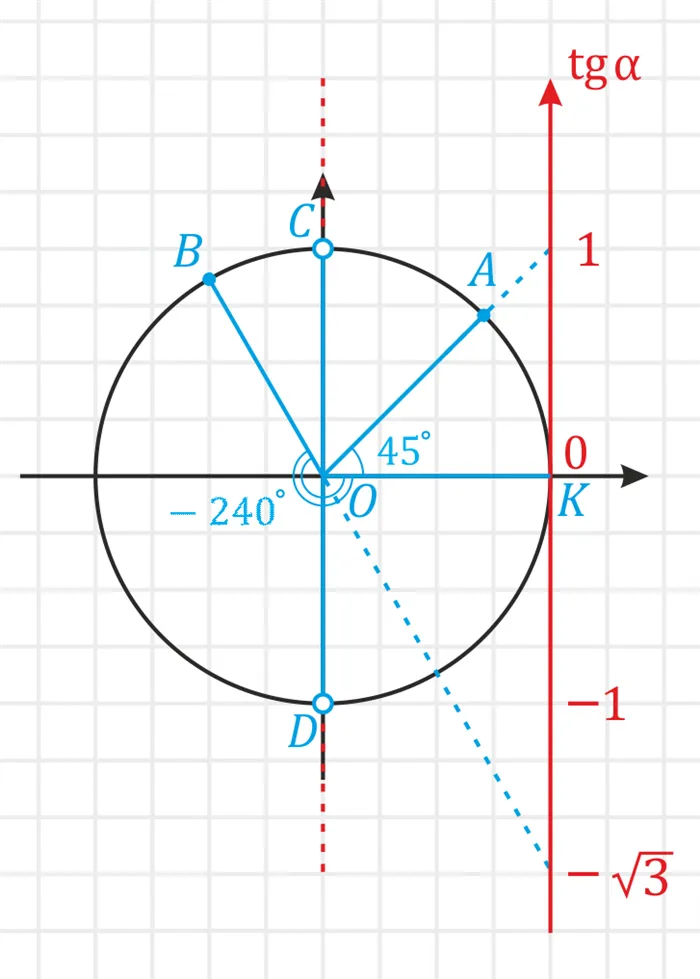
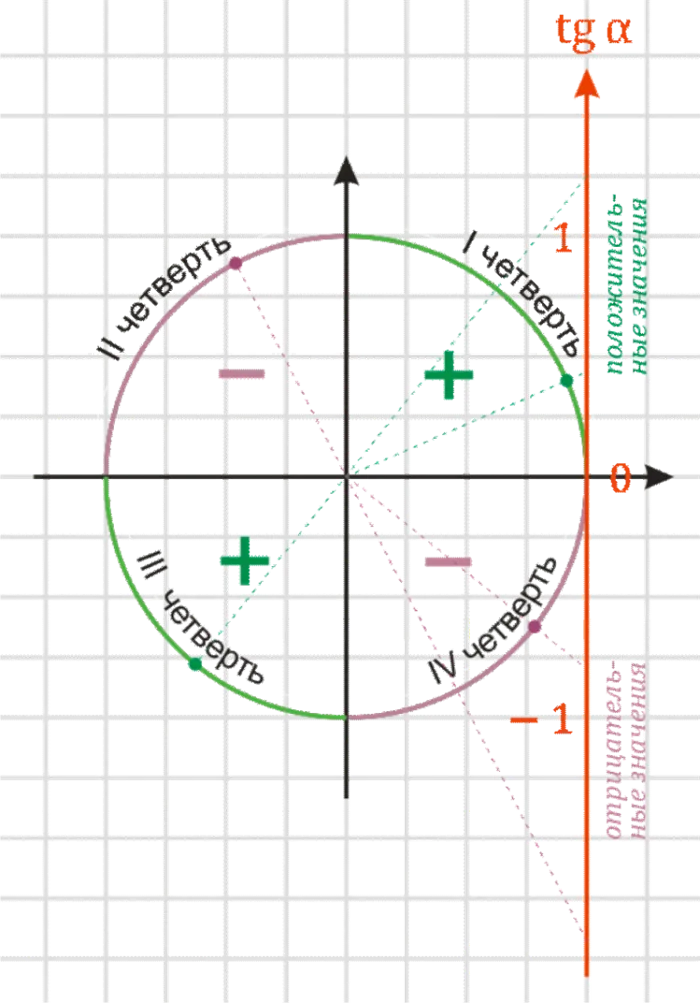
Знаки по четвертям
Использование касательных валов облегчает определение признаков4-й треугольного цикла. Для этого возьмите точки квадрата и определите знаки касательных, используя метод, описанный выше. Одни и те же знаки имеют одни и те же символы.
Например, на этой диаграмме показаны две зеленые точки в кварталах I и III. В этих случаях значения касательных положительны (зеленая пунктирная линия — положительная часть оси). Поэтому в любой момент в I и III кварталах значения касательных также положительны (знак плюс). Две фиолетовые точки в четвертях II и IV похожи, но со знаком минус.
Термины «касательная» (от лат. tangent — см.) и «секущая» (от лат. secant — квадратичный) были введены датским математиком Томасом Финке (1561-1656) в его книге Geometriarotundi (1583).
Тригонометрические функции и их значение в изучении геометрии
Тригонометрические функции играют особую роль в геометрии, определяя, как соотносятся между собой стороны и углы правильного треугольника. Конечно, тригонометрия не была статичной, и время Евклида было далеко вперед, что позволило выразить эти функции путем решения дифференциальных уравнений.
Сегодня для основных тригонометрических функций используется шесть обозначений, причем четыре из шести функций являются последними в ряду и могут быть определены способами, отличными от геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc)
Рассмотрим сам правильный треугольник. Названия его сторон и углов во всех справочниках, как обычно, стандартные — по обе стороны от плоскости.
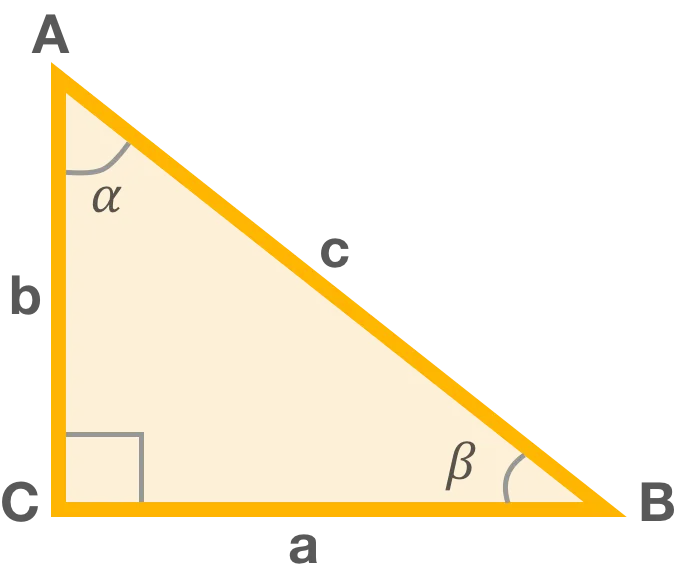
Треугольник имеет три угла, обозначаемые α, β и γ. γ всегда равен 90°. Другая сторона прямого угла γ называется гипотенузой и обозначается C. Угол α, с которого начинаются все вычисления, лежит на стороне α/ BC /, называемой противоположной стороной этого угла, и на стороне b/. AC / касательная к этому углу называется стороной касания.
Согласно евклидовой теории, которая по-прежнему актуальна (и всегда актуальна), сумма углов таких треугольников на одной плоскости равна 180 или числу пи. И для любого заданного значения угла между 0 и π/2.
Тригонометрические функции могут быть выражены через размеры сторон этого треугольника. Поскольку угол α является первым как в греческом алфавите, так и в треугольнике, мы начинаем знакомство с функциями с этого угла.
- Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
- Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
- Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b : tg α = а : b.
- Котангенс угла α в соответствии равен ctg α = b : а.
- Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
- Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.
Эти функции также можно представить в виде окружностей, определив систему координат. Дана система координат с центром O. Угол, на который поворачивается часть O, показанная на диаграмме, произволен и называется θ.
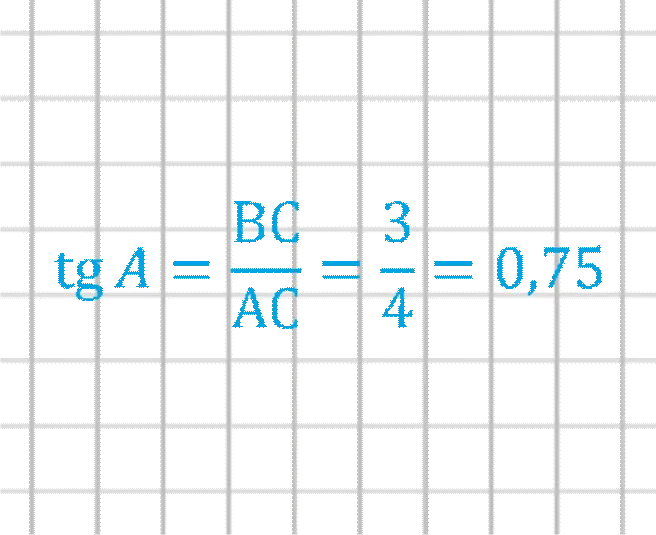
Тогда касательная к этому углу θ представляет собой отношение правого конца точки A к ее дистальному концу. Таким образом, если ctgα= b:α, AC =sinθ и OS =cosθ, то tgθ=sinθ:cosθ. Аналогично, ctgθ= cosθ:sinθ или 1:tgθ.
Тангенс — это отношение…
Таким образом, существует два определения.
Тангенс острого угла прямоугольного треугольника — это отношение перпендикуляра к соседнему треугольнику.
Тангенс — это отношение синуса к косинусу.
Вместо «касательная к углу альфа» пишется tga. В калькуляторах и различных программах для компьютеров и ПК распространено другое название: tan(a).
Применение функции тангенса для решения задач
Чтобы научиться пользоваться этой функцией, попробуйте решить несколько примеров ее использования.

Пример: у вас есть два катетера с BC =7 см и AC=12 см. Все остальные факты о треугольниках должны быть известны.
Первое уравнение — tgα= α:β. Тогда tgα = 7:12 = 0, 5833, затем используйте массив Брадиса для нахождения угла α. На пересечении градусов и минут находится самое близкое значение угла — 0,5844. Это соответствует 30° и 18′.
Найдите ближайшее значение 3 ‘поправки. Отведите от угла и получите угол α = 30°15′. Предполагая, что сумма всех углов не должна превышать 180°, найдите второй угол с контракцией угла γ = 90°. Тогда угол β = 90°-30°15′ = 59°45’.
Осталось найти нижнее значение c.
Мы можем найти его через грех а. Это равно a:c, тогда c = a:sin a.
Используйте таблицу Бразиса для нахождения sin. Ближайшее значение для 30°36′ равно 0,5060, затем 3′ и в соответствии с полем коррекции равно 0,0008. Прибавьте это число к найденным значениям: 0, 5060 + 0,0008 = 0,5068. Подставьте это значение в формулу c = 7: 0,5068, c = 13, 8 см. Проблема решена.
Мы можем найти значение угла через значение p, которое равно 180°. Далее тангенс 30°, тангенс 0°, тангенс 60°, тангенс 90°, тангенс 45°, тангенс 15° и тангенс 75° намного проще.. Следует отметить, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет особого значения.
Вы можете найти касательные к пятиградусным углам, которые равны 0, 0875 и могут быть добавлены или удалены от наиболее распространенных углов. Например, при угле 45 градусов ее тангенс равен 1, тогда тангенс при 50 градусах равен 1, 0875; тангенс при 35 градусах можно вычислить, добавив к тангенсу при 30 градусах 5 градусов; тангенс при 10 градусах равен 10 градусам. В два раза больше угла в 5 градусов.
Для удобства приведена расчетная таблица больших углов через цену P
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Следует помнить, что если угол больше 90 градусов, то функция имеет возможность повторения. Таким образом, если вы ищете тангенс 145 градусов, 180 — 145 = 35 градусов, но со знаком «минус». Как будет понятно из конструкции круга с положительными или отрицательными значениями для абсциссы и ординаты. Научиться быстро пользоваться таблицей Брадиса и вычислять цену треугольника совсем не сложно. Главное — понять природу процесса.
Рассмотрим сам правильный треугольник. Названия его сторон и углов во всех справочниках, как обычно, стандартные — по обе стороны от плоскости.
Что такое тангенс в прямоугольном треугольнике
Полутон угла треугольника является причиной стороны, противоположной определенному углу нижней части треугольника, а косинус — причиной стороны, следующей за подчиненной.
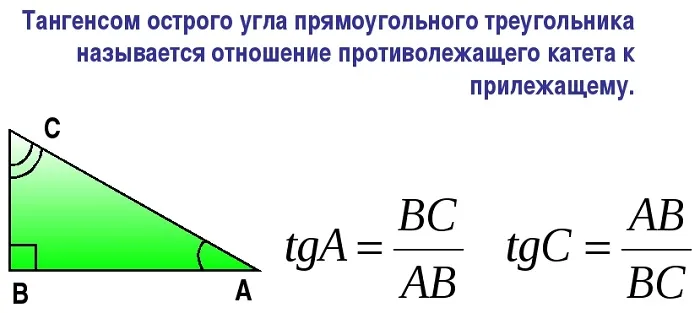
Затем, если вы разделите угловой полутон на косинус, вы возьмете тангенс (обозначенный как TG), а если вы разделите косинус на синус, вы возьмете цыпленка. Здесь все очень просто. Главное — знать кривые и треугольники треугольника.
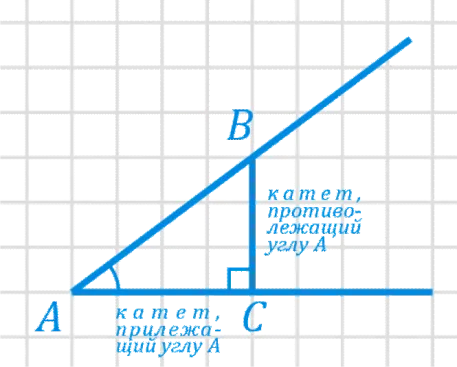
Также на графике в конце есть треугольные касательные, которые являются различиями между II указателями, но в данной статье они рассматриваться не будут, так как имеют лишь косвенное отношение к треугольникам.
Таблица тангенсов углов от 0° до 360°
Ниже приведена таблица цен. Это поможет вам быстро найти нужную цену.
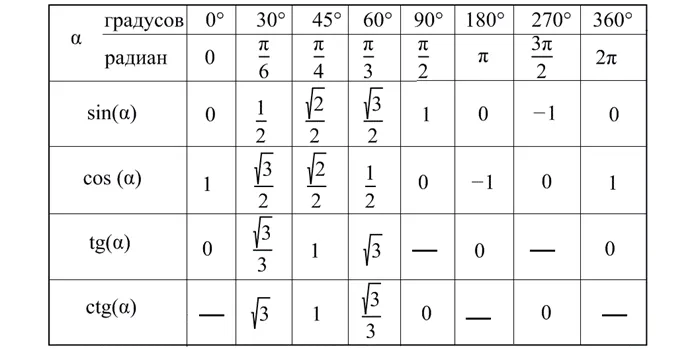
В качестве альтернативы вы можете поискать цены в Интернете или запомнить их. Наиболее эффективным методом для математиков являются печатные цены, но это непрактично для всех.
Примеры вычислений тангенса в прямоугольном треугольнике
Существует несколько методов и простых видов нахождения прямоугольных треугольников, касательных к прямоугольнику. Однако мы рассмотрим лишь некоторые из них.
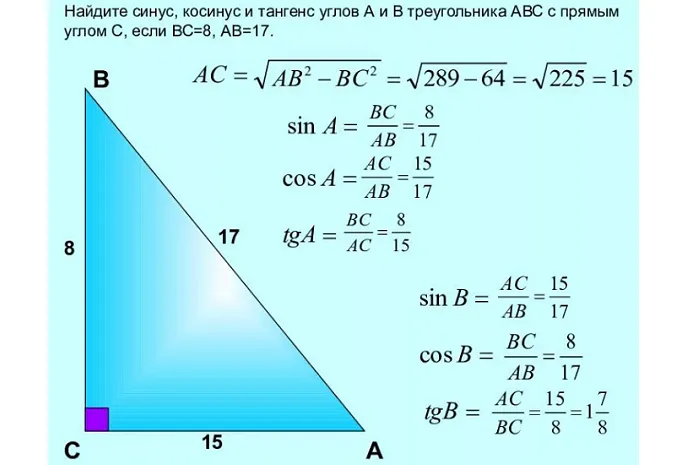
Секрет здесь прост, ведь все методы ограничиваются нахождением сторон — если вы знаете значения всех сторон, то тангенс угла A треугольника находится по следующему правилу: TGA = BC:AC, что означает, что TG A равен отношению противоположных смежных сторон.
Самое простое, что вы можете сделать, это найти касательную линию острого угла. Даже если это не угол прямоугольного треугольника, его можно легко добавить к прямоугольному треугольнику.
В этом суть касательных, но если нужно найти стороны, то это, конечно, не проблема касательных.








