Что такое равный треугольник. Что такое равный треугольник

Теорема синуса. Стороны треугольника пропорциональны синусу противоположного угла. Коэффициент пропорциональности равен диаметру окружности, описанной вокруг этого треугольника.

Что такое равный треугольник

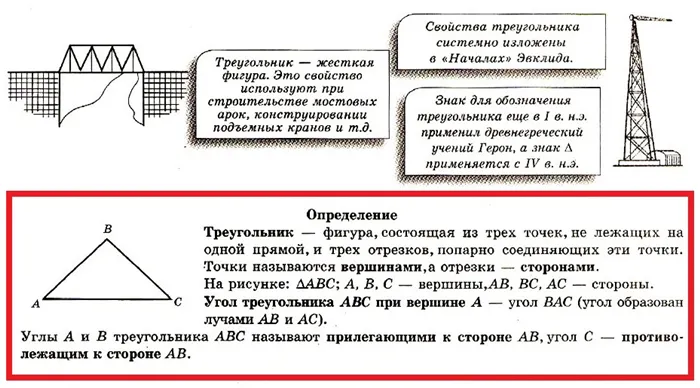
Треугольник — это диаграмма, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки по паре. Точки называются вершинами, а отрезки — сторонами.

Треугольник — это жесткая форма. Это свойство используется при изготовлении мостовых дуг и в строительстве кранов. Свойства треугольника систематически представлены в евклидовых элементах. Символ треугольника был внедрен в древнегреческую речь Героном с I века. С IV века используется символ D.

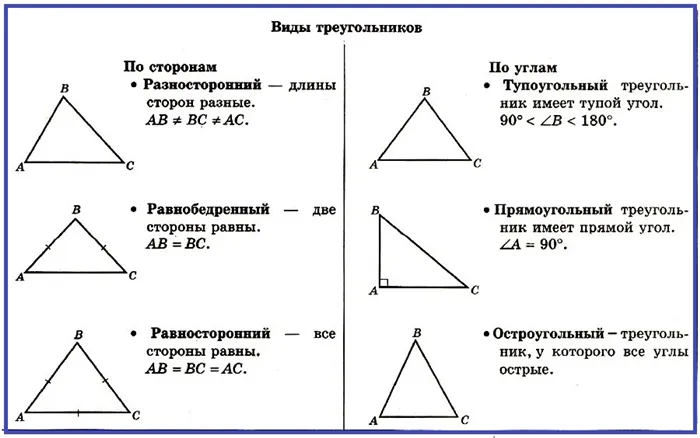
Медиана, биссектриса и высота треугольника

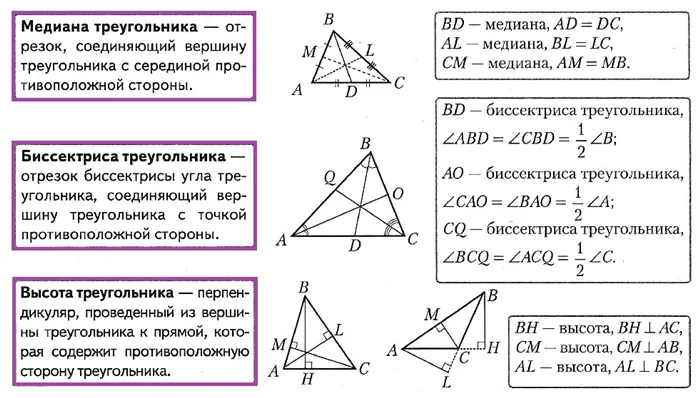
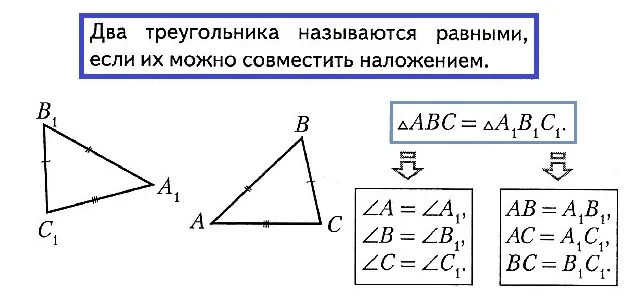
Управление треугольником, равным определенному треугольнику. Каким бы ни был треугольник, есть треугольники, которые равны тому или иному раскладу, по сравнению с той или иной полудемократией.

Признаки равных треугольников 1. В равных треугольниках соответствующие стороны равны. 2. в равных треугольниках соответствующие углы равны. 3. в равных треугольниках границы равны. 4. площади равных треугольников равны. 5. равные углы при равных сторонах. 6. есть равные стороны с равными углами.

Признаки равенства треугольников

Дополнительные точки равенства — если две стороны и медианы, проведенные к третьей стороне треугольника, равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, то эти треугольники равны. — Треугольник является буквальным, если два угла и высота равны двум углам, выходящим на смежные стороны треугольника, а высота выходит на смежную сторону треугольника. — Если сторона, высота и медиана, проведенные к одной стороне одного треугольника, равны стороне, то эти треугольники равны, если высота и медиана проведены к одной и той же стороне другого треугольника. — Если медиана и угол, делящий угол одного треугольника, равны медиане и углу, делящему угол другого треугольника, то эти треугольники равны.

Это обзор темы «Треугольники, равенство треугольников». Выберите следующий шаг.

В 2021 году геометрические задачи на шашечной бумаге не являются частью использования, но они очень полезны для начала изучения геометрии и понимания планет.

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать, наложив один треугольник на другой. Однако, согласитесь, это несерьезно: это проблема не равенства треугольников, а самих треугольников. Как мы можем иметь три теоремы и доказать их?

Рассмотрим три доказательства равенства треугольников.

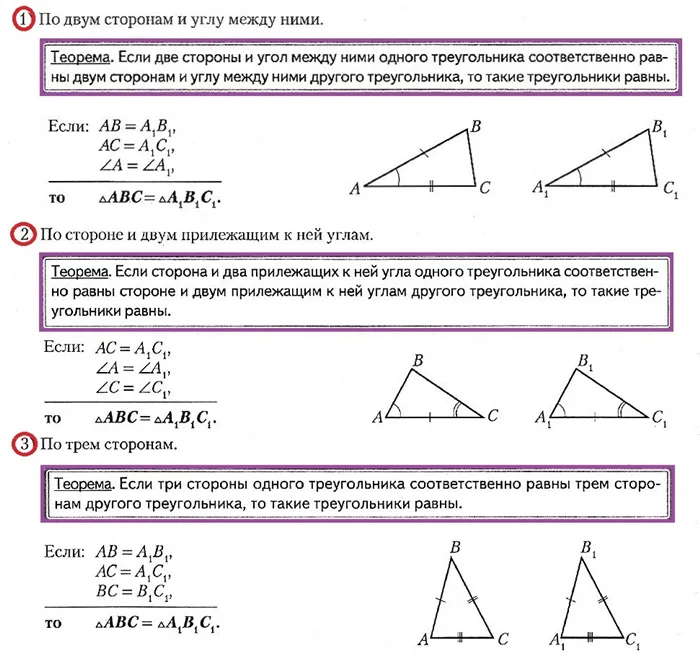
Теорема 1. Равенство треугольника с двумя сторонами и углом между ними.

Если угол между двумя сторонами и одного треугольника равен углу между двумя сторонами и другого треугольника, то эти треугольники равны.

Имеется переплата △a₁b₁c₁ Верхнее a с abc₁ Выровнены по верхнему a и боковому a₁b₁ Накладка на сторону ab, сторона a в ac₁c₁Выравнивается со стороной a в abc.

Сторона a₁b₁ Выровнена со стороной AB, верхняя часть b вдоль верхней части b₁сторона a₁Больше.₁ Выровнена со стороной AC, вершина C выровнена с вершиной C₁Выравнивается со стороной a в abc.

Это означает, что пики b и b₁c и c₁Выравнивается со стороной a в abc.

Изучайте математику с лучшими преподавателями на наших курсах математики для учащихся с 1 по 11 класс!

Второй признак равенства треугольников

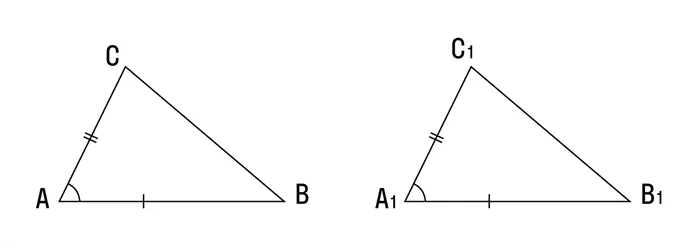
Теорема 2: Равенство треугольников с одной стороной и двумя смежными углами.

Если одна сторона одного треугольника и два смежных угла равны одной стороне и двум смежным углам другого треугольника, то эти треугольники равны.

По переплате △abc, △a₁b₁c₁, вершина a выравнивается с вершиной a₁и верхние b и b₁ на одной стороне.₁Больше.₁Выравнивается со стороной a в abc.

c₁c₁потому что мы знаем, что Ac = a₁c₁c₁Выравнивается со стороной a в abc.

b₁b₁.₁Выравнивается со стороной a в abc.

b₁b₁▪ b, ▪ c =∠C.₁Выравнивается со стороной a в abc.

▪ b, ▪c=c=∠C.₁Выравнивается со стороной a в abc.

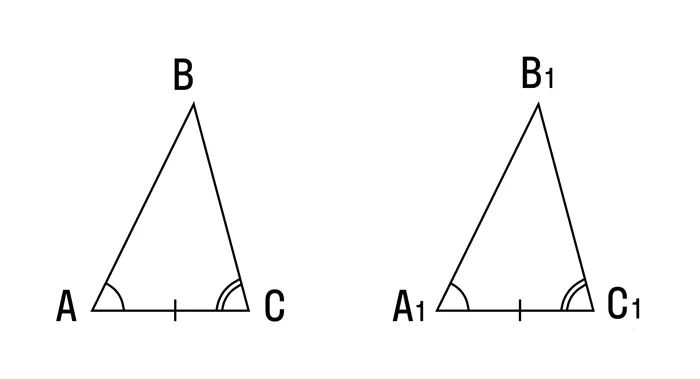
Третий признак равенства треугольников

Если три стороны одного треугольника эквивалентны трем сторонам другого треугольника, то эти треугольники равны.

Доказательство доказательства 3. Доказательство доказательства равенства треугольника:.

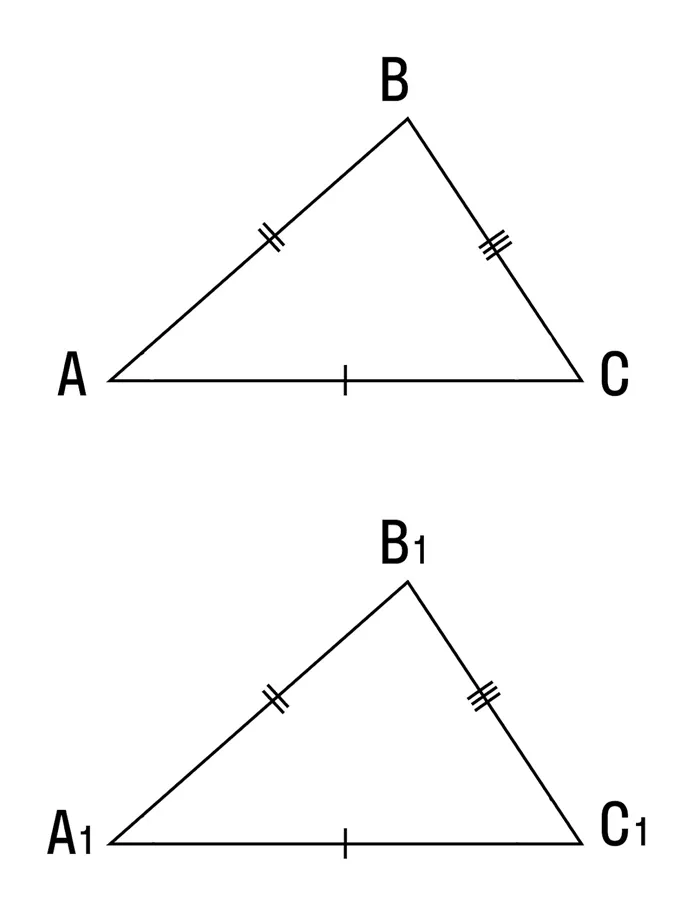
Применить ABC

b₁b₁c₁, от вершины b до вершины b₁, top c и top c₁ на противоположной стороне прямой.₁В₁В.₁Выравнивается со стороной a в abc.

Равны ли треугольники или нет, можно определить не только по их сторонам и углам, но и по их высотам, пересечениям и биссектрисам.

Как видите, для доказательства равенства треугольников можно использовать множество точек и десятки методов. Три точки равенства треугольника являются основополагающими. Поскольку треугольники — это, казалось бы, простые фигуры, все остальные методы также стоит запомнить.

1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Поэтому не все углы на внешней стороне треугольника имеют право называться внешними, а только углы, образованные на одной стороне и продолженные на противоположной стороне.

Равенство треугольников имеет три характеристики.

Признаки равенства

1. если угол между двумя сторонами и одного треугольника равен углу между соответствующими двумя сторонами и другого треугольника, то эти фигуры равны.

Рисунок 1.Первые признаки равенства

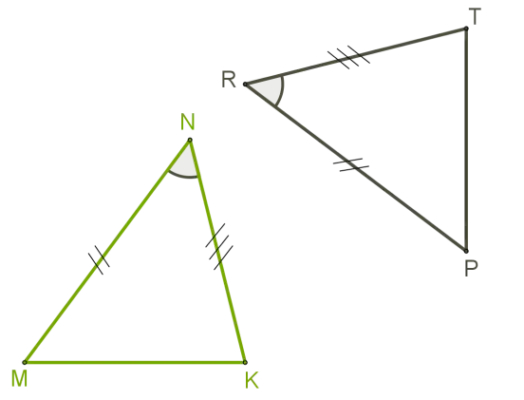
2.Эти фигуры равны, если угол между одной стороной и одним треугольником равен углу между соответствующей стороной и двумя смежными углами другого треугольника.

Рисунок 2.Второй знак равенства

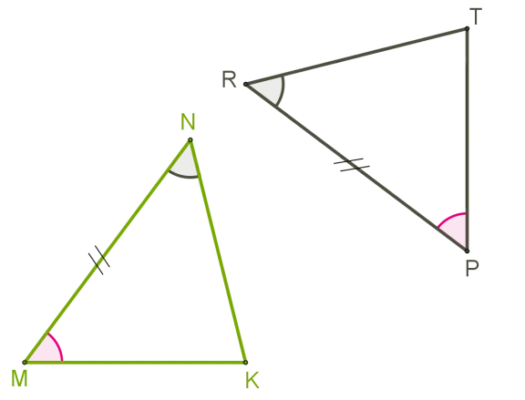
3 Если три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники равны.

Кроме того, стоит отметить несколько качеств.

Порядок имен в вершине одного треугольника должен быть таким же, как порядок имен в вершине другого треугольника.

• Сумма двух внутренних углов треугольника будет всегда меньше 180 0 .
• Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
• Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Алгоритм доказательства равенства фигур

• Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
• На рисунке отметить, все необходимые данные в условии задания.
• Проверить есть ли у двух треугольников общая сторона либо угол.
• Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
• При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
• При необходимости, можно сделать дополнительное построение.

Ножки лестницы могут свободно двигаться вместе, если они не закреплены перемычками. Жесткость таких конструкций основана на третьем пункте числового равенства.

Распределение:.

Пример

Две части пересекаются в точке o и расходятся от этой точки посередине. Докажите, что $ΔABO=ΔCDO$.Решение.

Стоит обратить внимание на цифрыКонвенция, о которой идет речь, предусматривает $ bo = od $ и $ ao = os $. А углы $ aob $ и $ cod $ равны, так как они перпендикулярны. Поэтому $δABO = ΔCDO$ в соответствии с первым знаком треугольного равенства.

В невоспроизводимых треугольниках сумма длин обеих сторон больше длины третьей стороны, а вырожденные треугольники равны. Другими словами, длины сторон треугольника связаны следующими неравенствами

Треугольник называется подобным, если его стороны пропорциональны.

Признаки подобия треугольников

Синус. Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.

II Синус. Если две стороны одного треугольника равны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то эти треугольники являются буквальными.

III Экспонат. Если три стороны одного треугольника подобны трем сторонам другого треугольника, то эти треугольники являются буквальными.

Более подробную информацию о сходстве между треугольниками см.

Следующая теорема применима к каждому треугольнику.

Теоремы треугольников

Теорема о Вселенной. Площадь одной стороны треугольника равна сумме площадей двух других сторон, минус удвоенное произведение этих сторон на косинус угла.

Подробнее о теореме Космита читайте по этой ссылке.

Примеры решения задач

Задание	Доказать, что в равнобокой трапеции диагонали равны.
Доказательство	В равнобокой трапеции рассмотрим треугольники и (рис. 1). Так как – общая сторона, то треугольники и равны по первому признаку, а значит, равны все их элементы, т.е. .

Если равенство пропорций соблюдено, то пропорциональны не только соответствующие стороны треугольника, но и общие углы. Следовательно, треугольник и — подобны (вторая точка подобия). Находит свою сторону:.

Задание	В треугольнике стороны см см см. На стороне отмечена точка так, чтобы см. Найти отрезок .
Решение	Рассмотрим треугольники и . Запишем отношение сторон и :

Конвенция, о которой идет речь, предусматривает, что $ bo = od $ и $ ao = os $. А углы $ aob $ и $ cod $ равны, так как они перпендикулярны. Поэтому $ d abo =Δcdo$ в соответствии с первым принципом треугольного равенства.

В невоспроизводимых треугольниках сумма длин обеих сторон больше длины третьей стороны, а вырожденные треугольники равны. Другими словами, длины сторон треугольника связаны следующими неравенствами

Признаки равенства треугольников

Два треугольника равны, если углы с обеих сторон и эти стороны равны.

Рассмотрим два ABC и треугольник

b₁ c₁в котором: a₁ ABC = a

b₁ c₁в котором: a₁Выравнивается со стороной a в abc.

c₁ c₁в котором: a₁ b₁ соединена с точкой AB, а точка b соединена с точками b₁ c₁ b₁ = ab. сторона a₁ c₁ Совместимость с переменным током, так как ∠A = ∠A₁в котором: a₁ a₁ c₁ = AC. сторона₁в котором: a₁ и BC согласны, потому что их цели совпадают. В результате треугольники совпадают. Теорема доказана.₁в котором: a₁Рассмотрим два ABC и треугольник

Второй признак равенства треугольников

b

b₁ c₁в котором: a₁ ABC = a

и угол A = угол A₁в котором: a₁.₁ ABC = a₁Выравнивается со стороной a в abc.

b₁ c₁в котором: a₁Выравнивается со стороной a в abc.

c₁ c₁в котором: a₁ b₁ соединена с точкой AB, а точка b соединена с точками b₁в котором: a₁ c₁ = AC. сторона₁в котором: a₁ Поскольку ∠A = ∠A, следует, что сторона AB₁ c₁ b₁ c=∠C, поэтому сторона CB следует₁ c₁ b и b совпадают с вершиной b₁ которые действуют как пересечения одного и того же участка. Следовательно, треугольники совпадают. Теорема доказана.₁Два треугольника равны, если три стороны одного треугольника равны трем другим сторонам.₁Рассмотрим два ABC и треугольник

Третий признак равенства треугольников

b

b₁ c₁в котором: a₁ ABC = a

c₁ c₁в котором: a₁Выравнивается со стороной a в abc.

c₁ c₁в котором: a₁и верхние b и b₁ находятся на противоположных сторонах прямой AC.₁Соединяя B и B₁возьмите два треугольника Isoscele bab.

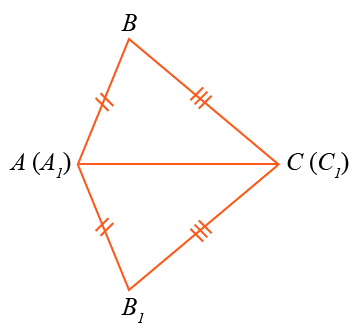
и BCB₁.₁С треугольным бабом.₁Выравнивается со стороной a в abc.

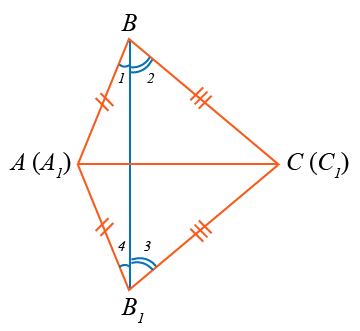
▪2 = ρ3 (как базовый угол). Поэтому.₁ ∠1 +∠2=ρ4 + am 3, поэтому ∠ABC= amAb₁ C.

Следовательно, ab = a₁ b

и bc = b₁ c₁и ∠ABC = ∠A₁в котором: a₁ c₁ c₁в котором: a₁Выравнивается со стороной a в abc.

c₁ c₁в котором: a₁ Примечание: В этом разделе указаны противоположные углы этих трех сторон (противоположные углы).

В невырожденном треугольнике сумма длин обеих сторон больше длины третьей стороны; в вырожденном треугольнике эти суммы равны. Другими словами, длины сторон треугольника связаны следующими неравенствами

Соотношения в треугольнике

Неравенство треугольника является одним из постов метрики.

Неравенство треугольника

Треугольник называется подобным, если его стороны пропорциональны.

где r — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a.

Теорема о сумме углов треугольника

Теорема синусов

= \ frac

(ǫ альфа- ǫ бета)>< b < c, то α < β < γ.

Теорема косинусов

Теорема тангенсов

(ɑ альфа+ ɑ бета)>. «ширина =» «высота =» » />Вычисление неизвестных сторон и углов треугольника на основе того, что известно, исторически называется «решением триангуляций». Используется общая теорема о триангуляции, приведенная выше.Неравенство распространяется на регионы.

Прочие соотношения

Метрические соотношения в треугольнике приведены для

Решение треугольников

Предположим, что вершины треугольника лежат на точках.

Площадь треугольника

Введите вектор площади Треугольник:.

• >R^2″ width=»» height=»» />, причём оба равенства достигаются.
• (a^2+b^2)» width=»» height=»» />, где равенство достигается для равнобедренного прямоугольного треугольника.

Вычисление площади треугольника в пространстве с помощью векторов

*

= \ frac12 \ begin 1 & y_a & z_a \ 1 & y_b & z_b \ 1 & y_c & z_c \ end «width =» height = «» />

Ў qquad s_z = \ frac12 \ begin x_a & y_a & 1 \ x_b & y_b & 1 \ x_c & y_c & 1 \ end «width =» height =» » />

Положим + S_y \mathbf+ S_z \mathbf» width=»» height=»» />, где ,

Площадь треугольника равна.

Альтернативный вариант — вычислить длины сторон (теорема Пифагора), а затем тип цапли.

Теорема Дезарга: если два треугольника являются точками зрения (прямые через соответствующие вершины пересекаются в одной точке), то соответствующие стороны пересекаются в одной точке.

Теорема Зонда: если два треугольника рациональны с точки зрения (вертикаль, падающая из вершины одного треугольника на противоположную сторону вершины треугольника и наоборот), то рациональным является и точка пересечения этих вертикалей, и будущий центр. Та же прямая, перпендикулярная точке зрения (прямая по теореме Дезарга).

Теоремы о треугольниках

Треугольник

Треугольник.