Натуральные числа — это числа, используемые для измерения конкретных конкретных объектов, таких как банан, две тетради или десять стульев.
Рациональные и иррациональные числа. Множество действительных чисел
Логическое число — это число, представленное обычной дробью m / n. где числитель m — целое число, а знаменатель n — натуральное число.
$ q = \ frac, m \ в \ Bbb Z, n \ в \ Bbb N \ если q \ в \ Bbb Q $
Множество рациональных чисел обозначается $\BbbbQ$.
Примеры рациональных чисел:.
Любое логическое число может быть выражено в виде конечной или циклической бесконечной дроби.
$ \ frac = 0.333 … = 0, (3); \ frac = 0, (428571); \ frac = $ 0,125
Несводимая логическая дробь m/n имеет конечное десятичное представление тогда и только тогда, когда первый делитель n равен только 2 и 5 разной силы. $ n = 2 ^ a \ cdot 5 ^ b, a, b \ ge 0 $
Алгоритм преобразования десятичных циклических дробей в обыкновенные дроби
Шаг 1: Для чисто периодических дробей запишите период дроби в числителе. Запишите целую дробь в числителе смешанной периодической дроби и вычтите из нее число перед периодом.
Шаг 2: Для чисто периодических дробей запишите знаменатель до девяти цифр периода.
Для смешанных периодических дробей напишите в знаменателе 9, столько же цифр, сколько в периоде, и добавьте ноль, столько же цифр, сколько в десятичной дроби перед периодом справа.
Шаг 3: При необходимости уменьшите полученную фракцию
Чистые периодические дроби:.
Смешанные периодические дроби:.
Множество логических чисел является измеримым. То есть, они эквивалентны множеству натуральных чисел: $ \ Bbb Q \ sim \ Bbb N $ (см. §11 данного руководства).

Слева — диаграмма для подсчета всех положительных рациональных чисел (соответствие один к одному между элементами множеств $ \ BbbQ_+ и Lo_BbbN $)
Множество рациональных чисел замкнуто для операций сложения, вычитания, умножения и деления (кроме деления на ноль). В алгебре говорят, что рациональные числа образуют поле.
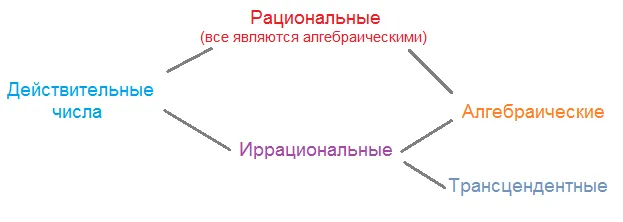
Иррациональные числа
Иррациональное число — это число, которое не может быть выражено в виде обычной дроби m / n. где числитель m — целое число, а знаменатель n — натуральное число. Иррациональное число можно выразить в виде бесконечной ациклической дроби.
Множество простых чисел обозначается $\mathbbI$.
Пример иррационального числа:.
$ \ sqrt 2; -⌘ sqrt3 7; pi; 20^0 none; e ^ 5; ln7; 0.01001000100001 … $
Множество неявных чисел не закрыто для акта сложения.
Невозможные числа можно аппроксимировать десятичными числами или рациональными дробями. Например, $ \ sqrt 2 $ можно записать как.
Числа $π\ около 3$, 14 или $π\ около\frac$ или $π≈\frac$- точность варьируется.
Мерой иррационального числа действительного числа α является действительное число μ, которое показывает, насколько хорошо число α может быть аппроксимировано рациональным числом.
Если $μ(a)=1 \a$ — рациональное число.
$μ(a)= 2\ против часовой стрелки$ — целое алгебраическое число
$μ(α)Ј ge2Ј против часовой стрелки$ — трансцендентное число
Для многих трансцендентных чисел мера иррациональности неизвестна, и существует только одна верхняя граница.
Алгебраические и трансцендентные числа
Если вещественное число является корнем уравнения вида
с целыми коэффициентами $c_i\ в \ Bbb Z $, такие числа называются алгебраическими.
Если вещественное число не является корнем такого уравнения с целыми числами, то такое число называется трансцендентным.
$ x ^ 2 = 4 \ Rightarrow x = \ pm 2, x ^ 2 = 2 \ Rightarrow x = \ pm \ sqrt 2, x ^ 3 = 2 \ Rightarrow x = \ sqrt 2 $
$ \ pm 2, \ pm√2, \ sqrt3 2 $ являются алгебраическими числами. В данном случае первая пара — рациональные числа, а остальные — иррациональные.
Примеры алгебраических чисел: $ 3,5 \ frac, ⌘ sqrt 3, ⌘ sqrt, ⌘ sqrt>, ⌘ sqrt521 $
Алгебраические числа могут быть рациональными и иррациональными.
Пример.
Все трансцендентные числа неразделимы.
Множество алгебраических чисел бесконечно и измеримо. То есть, они эквивалентны всем натуральным числам.
Множества алгебраических чисел закрыты для актов сложения, удаления, умножения и деления (кроме деления). В алгебре, говорят, алгебраические числа образуют поле.
Множество трансцендентных чисел бесчисленно.
Другими словами, трансцендентных чисел «больше», чем алгебраических. Их слишком много, чтобы представить их в виде последовательности.
С разумными числами вида 1 / n можно измерить небольшое количество, если n велико. Это создает обманчивое впечатление, что геометрические расстояния могут быть измерены разумными числами. Легко показать, что это не так.
Свойства рациональных чисел
Предположим, что a, b и c — рациональные числа.
Переместительные и сочетательные законы
a + b = b + a, например, 2 + 3 = 3 + 2;
a + (b + c) = (a + b) + c, например, 2 + (3 + 4) = (2 + 3) + 4;
a + (a) = 0, например, 2 + ( — 2) = 0
Переместительные и сочетательные законы при умножении
a x b = b x a, например, 2 x 3 = 3 x 2
a x (b x c) = (a x b) x c, например: 2 x (3 x 4) = (2 x 3) x 4
a x 1/a = 1 ≠ 0 — например, 2 x 1/2 = 1
Так как a x b = 0, то либо a = 0, либо b = 0, либо оба равны нулю.
Распределительный закон умножения
(a + b) x c = a c + b c, например, (2 + 3) x 4 = 2 x 4 + 3 x 4
(a -b) x c = a c -b c, например, (3 — 2) x 4 = 3 x 4 — 2 x 4
Иррациональные числа
Иррациональные числа являются противоположностью рациональных чисел, которые не могут быть записаны в виде простых дробей.
- число Пи = 3,14159. его можно записать как 22/7, но это будет лишь приблизительно и далеко не точно ( 22/7 = 3,142857..);
- √2 и √99 — иррациональные, т. к. их невозможно записать дробью (корни часто иррациональные, но не всегда);
- e (число) = 2,72 — иррациональное, т. к. его невозможно записать дробью;
- золотое сечение φ=1,618. — иррациональное, т. к. его невозможно записать дробью.
Иррациональный набор чисел обозначается буквой «i».
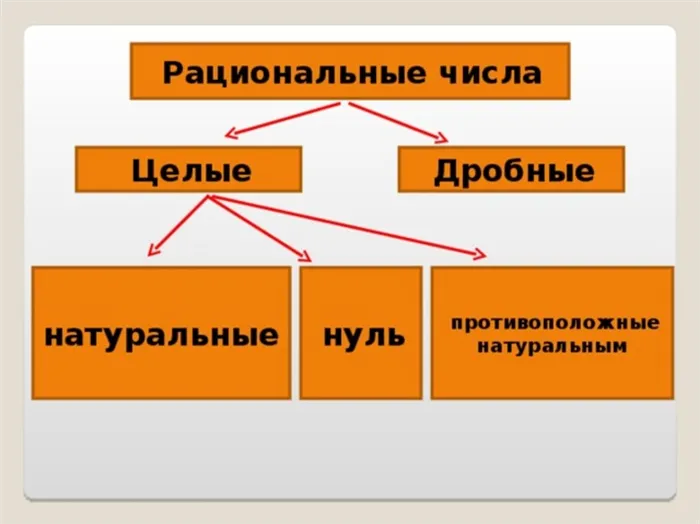
Какая разница между целыми, натуральными и рациональными числами
Целые числа — это натуральные числа, противоположные (меньше нуля) и ноль.
Все целые числа являются рациональными числами (включая натуральные), поскольку их можно выразить в виде дроби.
Множество целых чисел обозначается буквой z математика.
Натуральные числа
Единственными натуральными числами являются целые числа, начинающиеся с 1.
Ноль не является натуральным числом, потому что это число возникло естественным образом, когда люди еще считали на пальцах и не знали цифр («У меня столько коз, сколько пальцев на обеих руках»).
Множество физических чисел в математике обозначается буквой n.
Чтобы восстановить исходные пропорции, смешанные числа необходимо преобразовать в неправильные дроби. При использовании старого правила, т.е. умножения целой дробной части на знаменатель дробной части и прибавления дробной части к результату. Существуют следующие несоответствия.
Определение иррационального числа
Иррациональное число — это деление двух целых чисел, т.е. действительное число, которое нельзя выразить в виде рациональной дроби.
Она может быть выражена в виде бесконечного числа нецелых десятичных чисел.
Неопытная дробная десятичная дробь — это дробь, в которой дробные десятичные цифры повторяются как группа цифр или как одно и то же число.
- π = 3,1415926.
- √2 = 1,41421356.
- e = 2,71828182…
- √8 = 2.828427.
- -√11= -3.31662…
Название набора иррациональных чисел: латинская буква i.
Все действительные или реальные числа имеют рациональные и иррациональные числа. Положительные, отрицательные и нулевые.
Свойства неразделимых чисел:.
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, используемые для измерения конкретных конкретных объектов, таких как банан, две тетради или десять стульев.
И не совсем натуральные числа:.
- Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
- Отрицательные числа: -1, -2, -3, -4.
- Дроби: 1/2, 3/4, 5/6.
Целые числа — это натуральные числа, противоположные и нули.
Если два числа отличаются одним символом, они называются противоположными: +2 и -2, +7 и -7. Знак плюс обычно не пишется. Если числу не предшествует символ, оно означает положительное значение. Числа, которым предшествует символ минус, называются отрицательными числами.
Мы уже знаем, что такое разумное число из первой части статьи. Давайте посмотрим еще раз.
Разумные числа — это конечные дроби и бесконечные периодические дроби.
Каждое разумное число может быть выражено в виде дроби, числитель которой принадлежит целому числу, а знаменатель — целому числу. Таким образом, множество логических чисел включает в себя все целые и натуральные числа.
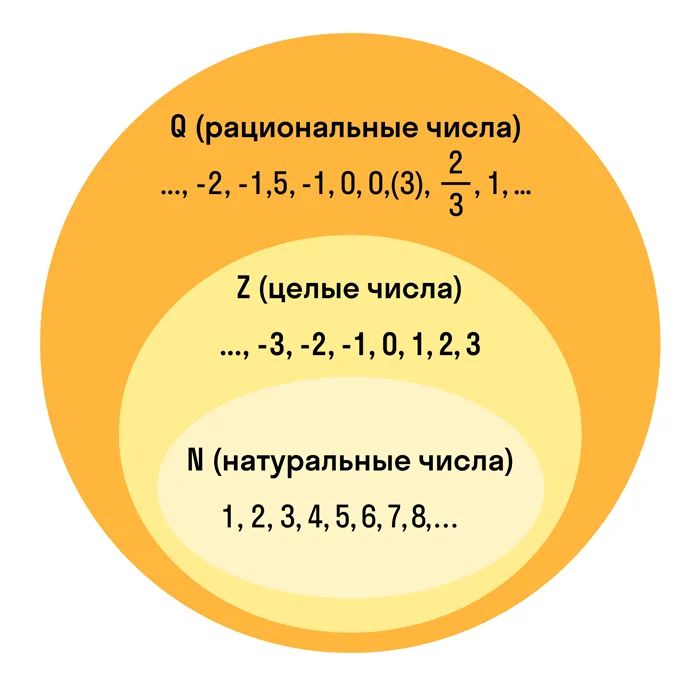
Однако не все числа можно назвать разумными. Например, бесконечная ациклическая дробь не принадлежит всем рациональным числам. Поэтому √3 или 𝜋(p) нельзя назвать рациональным числом.
Рациональное число — это число, которое может быть выражено в виде положительной или отрицательной пропорции или в виде нуля. Если число может получиться в результате деления двух целых чисел, то это рациональное число.
Числа. Рациональные числа.
Разумное число — это число, выраженное в виде нормальной пропорции m/n, где числитель m — целое число, а знаменатель n — натуральное число. 2/3.
Что такое разумное число? Рациональные числа (в отличие от иррациональных) — это числа с положительным или отрицательным знаком (целые и дробные) и нулем. Более точное понятие рациональных чисел выглядит следующим образом
Рациональное число — это число, выраженное обычной дробью m/n, где числитель n — целое число, а знаменатель n — натуральное число, например, 2/3.
Бесконечные ациклические дроби не принадлежат ко всем разумным числам.
Таким образом, число π (π = 3,14 …), основание натурального логарифма, E (E = 2,718 …) или √2 не являются разумными числами.
Разумные числа, например
Множество рациональных чисел.
Множество рациональных чисел обозначают
Дробь также может быть описана разными способами и видами, но ее значение от этого не теряется. Например, 3/4 и 9/12 (дробь, которая может получиться из другой пропорции (и наоборот) путем умножения или деления числителя и знаменателя на одно и то же натуральное число, является одним и тем же разумным числом). Разделив числитель и знаменатель дроби, мы получаем единственное представление рациональных чисел, которое нельзя уменьшить, поэтому мы можем говорить о них в целом
Множество логических чисел является естественным обобщением всех целых чисел. Если рациональное число a = m/n имеет знаменатель n = 1, то a = m — целое число.
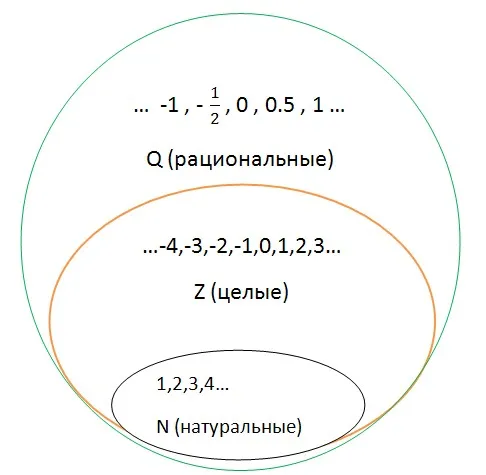
Каждое рациональное число просто выражается в виде дроби, числитель которой — целое число, а знаменатель — натуральное число.
Использование рациональных чисел в реальной жизни.
В реальной жизни ряд разумных чисел используется для подсчета определенных частей делителей целых чисел. Например, их разрезают на пирожные или другие продукты перед употреблением, или для аппроксимации пространственных отношений некоторых объемных объектов.
Основные свойства рациональных чисел следующие
1.Заказ.. Рациональные числа a и b имеют правило, позволяющее бесспорно отождествлять их1 — но только одно из трех отношений является «» или «». Это правило является правилом компоновки и излагается следующим образом.
2.Добавить режим.. Для каждого рационального числа a и b существует правило суммирования, которое дает определенное рациональное число c. Само число γ является суммой α и β, определяемой как (α+β), а процесс нахождения этого числа называется суммированием.
Правила суммирования следующие.
3.3.Акт умножения. Каждое логическое число a и b имеет правило умножения, которое связывает их с определенным логическим числом c. Число c называется произведением a и b, обозначается (a-b), а процесс нахождения этого числа называется умножением.
4.4.Переход классовых отношений. Для трех рациональных чисел a, b и c, если a меньше b и b меньше c, то a меньше c. Если a равно b и b равно c, то a равно c.
5.5.Заменяемость протезов.. Изменение позиции рациональной суммы не меняет саму сумму.
6.6.Подключение протеза.. Порядок, в котором складываются три рациональных числа, не влияет на результат.
7.Наличие нулей.. Существует рациональное число 0, которое сохраняет другие рациональные числа при сложении.
8.8.Существование противоположных чисел.. Каждое рациональное число имеет противоположное рациональное число, которые при сложении равны 0.
9.9.Инвертируемость умножения.. Изменение положения рационального множителя не изменяет произведение.
10.10.Соединения умножения.. Порядок умножения трех рациональных чисел не влияет на целое.
11.11.Существование одного.. Существует рациональное число 1, которое сохраняет другие рациональные числа в процессе умножения.
12.12.Существование обратного числа.. Каждое рациональное число, отличное от нуля, имеет обратное рациональное число, если умножить его на 1.
13.13.Дистрибутивность умножения по отношению к сложению.. Акт умножения связан со сложением законом распределения.
14.Отношение порядка к акту сложения.. К обеим сторонам логического неравенства прибавляется одно и то же логическое число.
15.Связь между отношениями порядка и актами умножения.. Одно и то же неотрицательное логическое число может быть перемножено в левой и правой частях логического неравенства.
16.16.Кабинет Архимеда.. Каким бы ни было логическое число a, легко получить столько единиц, сколько их сумма больше a.
Благодаря координатным линиям мы можем понять, почему брутто -2,5 расположено слева. Знак минус означает, что двухшаговое число сдвинуто влево. Удар был зафиксирован на отметке -2. Затем он смещается еще на один полутон, до середины между -3 и -2.
Перевод смешанных чисел в неправильные дроби
Для преобразования смешанного числа в неправильную дробь, как известно, целая часть умножается на знаменатель дробной части и прибавляется к числителю дробной части. Полученное число является числителем новой дроби, а знаменатель остается прежним.
Например, преобразуем смешанное число в неправильную дробь
Умножьте целую часть на знаменатель дробной части и прибавьте числитель дробной части.
Рассчитайте по этой формуле.
Полученное число 5 является числителем новой дроби, а знаменатель остается прежним.
Полная процедура выглядит следующим образом
![]()
Чтобы вернуть исходное смешанное число, просто вычтите целую дробь.
Однако этот метод преобразования смешанного числа в неправильную дробь применим только в том случае, если смешанное число положительное. Для отрицательных чисел этот метод не работает.
Рассмотрим дробь. Выберите целую дробь. Получите.
Чтобы восстановить исходные пропорции, смешанные числа необходимо преобразовать в неправильные дроби. При использовании старого правила, т.е. умножения целой дробной части на знаменатель дробной части и прибавления дробной части к результату. Существуют следующие несоответствия.

Дробь была получена и должна была получить дробь.
Мы делаем вывод, что смешанное число не было правильно преобразовано в неправильную дробь.
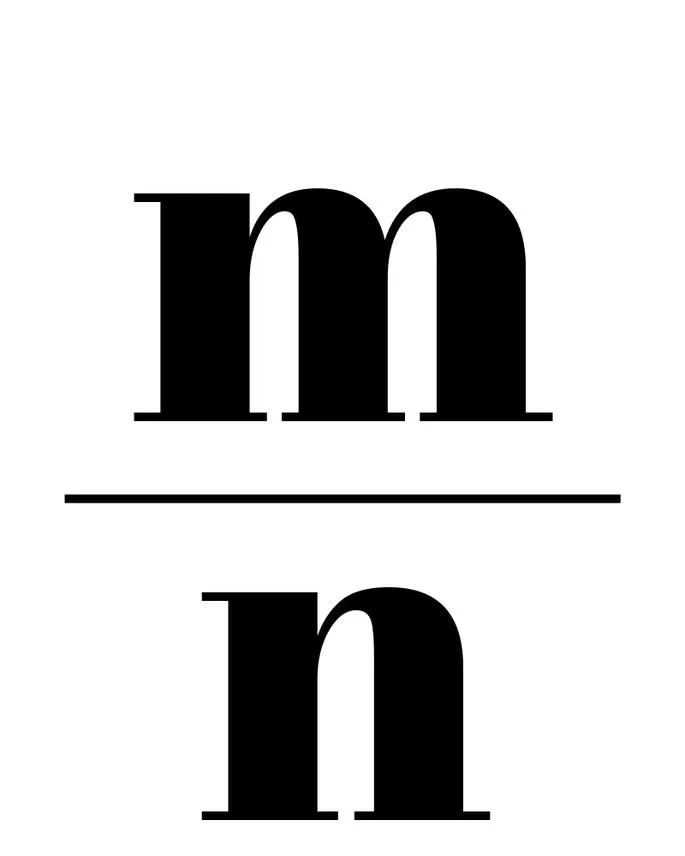
Чтобы правильно преобразовать отрицательное смешанное число в неправильную дробь, умножьте целую часть на знаменатель дробной части и вычтите числитель дробной части из полученного числа. В этом случае все выравнивается правильно.

Отрицательное смешанное число является противоположностью смешанного числа. Если положительное смешанное число находится справа и является
Затем отрицательное смешанное число располагается симметрично слева по отношению к первому

и «два целых числа и одна секунда», затем «минус два целых числа и минус одна секунда». Число -2 находится слева от координатной прямой, поэтому оба числа отрицательны.
17 thoughts on “Рациональные числа”
Лучше, если после каждого шага будет задаваться много вопросов. Без заданий невозможно запомнить предмет. Не существует случая, когда «один вопрос и пять ответов» применимы. Человек должен убедиться, что он правильно решил задачу.
На каждом этапе есть несколько примеров. Прочитав условия, вы можете попробовать решить примеры самостоятельно.
Мне было очень приятно прочитать материал и обновить свои знания. Жаль, что нет продолжения. Все очень понятно, спасибо.
Здравствуйте, админ! Мне очень понравилось повторять математику. Не могли бы вы рассказать нам о вашей следующей теме?
Спасибо за сайт, мне нравится узнавать то, что я потерял много лет назад. Однако хотелось бы знать профессию и квалификацию автора, а также то, достиг ли администратор высшего разряда по математике.
Вам необходимо написать руководство к вашей статье, которое, я уверен, будет очень полезным. Если наша книга будет очень понятной, каждый станет отличником.
Здравствуйте, мы все еще учимся, товарищ Ленин говорил, что учиться никогда не поздно, и я тоже хочу видеть высшую математику в управлении.








