Можно обнаружить пары, разница между которыми равна 2. При объединении они получают значения, кратные трем. Их называют парами или близнецами. Исключение составляют первые две цифры серии — 3 и 5. Это происходит потому, что сумма, полученная в результате сложения, не может делиться на три.
Better Explained: непростой взгляд на простые числа
Первые номера в математике — это настоящие голливудские звезды. Они у всех на устах, но никто не знает секрета их успеха. Еще одна публикация более понятного перевода дает хорошее соотношение между первыми номерами и химическими веществами.
Математики любят проводить время за поиском самого большого известного первого числа. Это здорово, но поверьте, гораздо лучше приблизить первые цифры к людям и рассказать им о том, что бесконечно полезнее.
Вот два неопровержимых доказательства холодности первых чисел
- Простые числа — это строительный материал для всех остальных чисел. В химии знание химического состава вещества помогает спрогнозировать его свойства. С числами всё происходит точно так же!
- У простых чисел есть особые свойства, например, трудность их определения. Да, порой такая черта может быть оказаться весьма положительной — в таких сферах, как криптография.
Так что такое простые числа?
Фундаментальная теорема арифметики гласит, что каждое число может быть описано как произведение первых чисел. Например:.
Первое число — это следующие неделимые числа. Например, 3, 5, 7 или 23. и число 2 также является первым числом.
1 — это особое число, которое не считается первым, только во избежание шизофрении, например, 1 = 1 * 1 * 1 * 1 * 1 * 1.

Джексон Поллок, «Номер 1», 1950 год, пример абстрактного импрессионизма.
Представление натуральных чисел в виде произведения первого числа называется факторизацией или делением на простые числа. Деление на первые числа кажется простым. На самом деле, все не так просто. Доказано: это так.
- Ряд простых чисел бесконечен;
- Не существует алгоритма составления ряда простых чисел;
- Простые числа играют решающую роль в самых неожиданных матчах, например, в квантовой механике;
- Разложение на простые — это сложно. Пока что метод перебора является лучшим способом факторизации. А это очень медленно.
Другими словами, неизвестный монстр из макарон создал первые числа, воспроизвел еще большее их количество и попытался разбросать их повсюду.
Аналогия: простые числа и химические формулы
Первые номера похожи на индивидуумов. Мы можем записывать натуральные числа в виде химических формул, чтобы описать их детали. Мы можем написать молекулы воды, как в химии.
h2O = два атома водорода и один кислород.
В математике мы пишем числа, используя первую цифру.
12 = 2 * 2 * 3 = 2 2 * 3 = два 2 яруса и триада.
Единственное отличие заключается в том, что в химических формулах «степень» пишется внизу, а не вверху. Я написал в Американский союз химиков, чтобы убедить их внести необходимые изменения в свою систему памяток, но они мне так и не ответили.
Это интересное наблюдение. Что если периодическая система химических элементов поможет найти закономерности во всех первых числах?
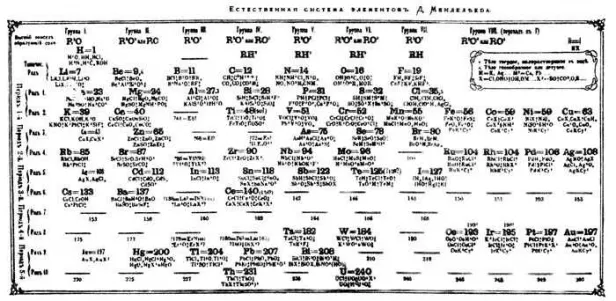
Менделеев, Д.И. 1871.
Давайте посмотрим, как это делали химики с помощью таблиц в журналах.
- Пустые ячейки в таблице указывали на появление новых элементов;
- Элементы одного ряда или колонки таблицы обладали сходными свойствами;
- В таблице прослеживались закономерности в поведении элементов, например, увеличение химической активности.
Если бы только существовала такая таблица для первого номера!
Вопрос в том, как бы вы это сделали? Никто не знает, как будет выглядеть этот стол. Первый набор чисел бесконечен, и как бы вы ни старались составить алгоритм появления, у вас все равно ничего не получится. Мы не знаем, где в этой таблице находятся пустые точки или сколько ячеек повторяется в свойствах. Есть несколько странных случаев, но загадка не решена.
Даже если мы не знаем всех подробностей личной жизни этих уникальных простых чисел, нам от них никуда не деться.
Они широко используются в шифровании, когда необходимо зашифровать важную информацию. Шифрование актуально для всех, поскольку оно используется для электронной почты, банковских карт. Даже мобильная связь защищена кодами.
Простые числа до 1000
Очень простой способ узнать, является ли число первым, — разделить его на первое число и посмотреть, получится ли целое число. Если первый шаг получает целое число, то первый — нет.
Если первое деление не является целым числом, попробуйте разделить его с другим первым числом, например, 5, 7 или 11. (Делить на 9 не нужно, так как это не первое число, а на 3, которое уже делится).
Более структурированным методом является сито Эратосфена.
Решето Эратосфена
Это алгоритм для нахождения первого числа. Требуется:.
- Записать все числа от 1 до n (например, записываются все числа от 1 до 100, если нужны все простые числа между ними);
- Вычеркнуть все числа, которые делятся на 2 (кроме 2);
- Вычеркнуть все числа, которые делятся на 3 (кроме 3);
- И так далее по порядку со всеми невычеркнутыми числами до числа n (после 3 это 5, 7, 11, 13, 17 и т. д.).
Все числа, не удаленные в конце этого процесса, являются первыми числами.
Взаимно простые числа
Это натуральные числа с единственным общим делителем 1. Например
- 14 (это 2 х 7) и 15 (это 3 х 5), единственный общий делитель — 1; если числа следуют одно за другим (как 13 и 12 либо 10 и 11), то они всегда будут взаимно простыми ;
- 7 (это 7 х 1) и 11 (это 11 х 1) — это два простых числа, а значит единственный общий делитель всегда будет только единица, простые числа всегда являются взаимно простыми ;
- или 30 и 48 не являются взаимно простыми, т. к. 6 х 5 = 30 и 6 х 8 = 48 и 6 — это наибольший общий делитель, т. е.: НОД (30; 48) = 6.
21 декабря 2018 года в рамках программы Great Internet Mersenne Prime Search (программа, направленная на поиск новых чисел Мерсенна) было найдено новое самое большое известное первое число.
Алгоритмы поиска и распознавания простых чисел

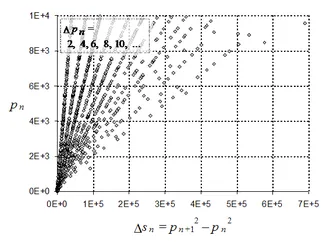
Простой способ найти оригинальный список первых чисел, пока некоторые цены не дают сетка Эратосфена, сетка Сундарама и сетка Аткина.
На практике, однако, часто бывает необходимо проверить, является ли конкретный номер первым, вместо того, чтобы получить список первых номеров. Алгоритм, который решает эту проблему, называется тестом простоты. Существует множество полиномиальных тестов первых чисел, большинство из которых вероятны (например, тест Миллера-Рабина) и используются в криптографических целях. В 2002 году было доказано, что тест на простоту полиномиально разрешим в общем виде, но предложенный тест на детерминант Агравала-Каджала-Саксены имеет очень большую вычислительную сложность, что затрудняет его применение.
Для нескольких категорий чисел существуют специальные эффективные тесты на простоту (см. ниже).
Бесконечность множества простых чисел
Первое число бесконечно. Самое раннее известное свидетельство об этом было подробно изложено Евклидом (Книга IX, утверждение 20). Доказательства можно резюмировать следующим образом.
Представьте, что первое число конечное. Умножайте их и добавляйте. Полученное число не делится ни на одно из конечного множества исходных чисел. Это означает, что число должно быть разделено на первое число, не включенное в общий итог. Противоречие.
Математики предложили другие доказательства. Одна из них (данная Эйлером) показывает, что сумма цен, обратных первым n -числам, бесконечно возрастает при увеличении n.
Теорема, распределяющая первое число, утверждает, что таким образом обозначается количество первых чисел, меньших n.
Наибольшее известное простое
Долгое время наблюдались рекорды, которые отмечали самое большое известное на тот момент первое число. Один из рекордов был когда-то установлен Эйлером. Эйлер нашел первое число.
Наибольшее известное первое число с февраля 2011 года. 12 978 189 Он содержит десятичные числа и является первым числом Мерсенна (M43112609). Он был найден 23 августа 2008 года математическим факультетом Калифорнийского университета в рамках проекта Gimps (Distributed Mersenne Prime Number Search Project), программы поиска первых чисел Мерсенна.
Для чисел Мерсенна существует эффективный тест на простоту: тест Люка-Лемера. Первое число Мерсенна долгое время было рекордсменом по самому большому известному первому числу.
За нахождение первых чисел с местами выше 100 000 000 000 и 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 EFF присудил 2 и 250 000 долларов США соответственно. Ранее EFF присуждала призы за нахождение первых чисел с десятичными знаками 1 000 000 000 и 10 000 000 000.
Фундаментальная теорема арифметики гласит, что каждое натуральное число, большее единицы, можно выразить в виде произведения простых чисел с точным набором коэффициентов. Поэтому первое число является фундаментальным «строительным блоком» натуральных чисел.
Наименьшее и наибольшее простое число
Оно делится само на себя, и одно есть два. Это единственное первое значение, которое может быть игом. Остальные всегда делятся на два. Другими словами, требуется третий делитель.
Поскольку существует множество первых чисел, и эти числа имеют тенденцию к бесконечности, невозможно узнать самое большое из них.
Невыводимость ряда была доказана еще до нашей эры Евклидом. Он предложил дополнить их диффузией всех известных исследуемых величин.
Это разделение в любом случае оставляет баланс. Это означает, что его нельзя отнести к комплексу. Это противоречит тому факту, что были использованы все известные простые числа, включая более крупные. Таким образом, конечный случай серии неверен.
В настоящее время известно около 25 миллионов значений сигналов. Это принадлежит к самому большому числу, обнаруженному наукой. Это 2.82.589.933.
Множество простых чисел
Множество — это совокупность общих свойств и интегрированных элементов.

Для изучаемых предметов это
принадлежат натуральному множеству, и
Существует максимум два делителя.
Первое число можно найти с помощью решетки Эратосфена. Запишите все значения, с которыми вы собираетесь работать. Выберите самый маленький и удалите его, затем продолжите с несколькими.
Например, в последовательности 1-100 первым таким объектом будет 2. Поэтому нужно разделить число на 2 и выделить его (т.е. разделить все значения на 2).
Наконец, выберите из остатка новый основной, найдите умножение и удалите его. Повторяйте до тех пор, пока это не станет возможным.
Наконец, все соединения удаляются.
Эратосфен использовал свои выводы следующим образом. Он брал папирус, писал на нем нужные значения и, выбирая их, накалывал неподходящие острыми предметами (отсюда название «грех Эратосфена»). Таким образом, они как бы просеиваются и должны оставаться в списке.
Некоторые свойства простых чисел
Отличительные характеристики объединяются в теоремы, посты. Многие из них лежат в основе математических правил, используемых сегодня.

Теория чисел изучена, но при использовании формул первое число обозначается буквой n.
Известны следующие правила:.
Если рассмотреть два первых числа (n), одно из которых делится на другое, то можно сказать, что они равны.
Все являются ненужными числами, кроме двух.
Можно обнаружить пары, разница между которыми равна 2. При объединении они получают значения, кратные трем. Их называют парами или близнецами. Исключение составляют первые две цифры серии — 3 и 5. Это происходит потому, что сумма, полученная в результате сложения, не может делиться на три.
Для каждой физической величины, большей 1, существует n больше нее. В этом случае физическая величина перекрытия больше n.
Если любые два n делятся на n, то произведение также делится на него.
Любое n, исключающее n, может быть отнесено к n или выражено как произведение.
Если вы возьмете комплексное число и проанализируете его на кратные n, то найдете такое, квадрат которого меньше исходного составного.
Некоторые n имеют пары, которые можно найти, перевернув n. Например, 13 и 31, 37 и 73. то же самое относится и к 3D n: 107 и 701, 709 и 907.
Если N увеличить до степени, представленной n, а затем вычесть N, то полученное значение будет кратно используемому n. Это правило является Малой теоремой Ферма.
Математики любят проводить время за поиском самого большого известного первого числа. Это здорово, но поверьте, гораздо лучше приблизить первые цифры к людям и рассказать им о том, что бесконечно полезнее.
Найти простое
Одним из способов определения простых чисел является «тест на простоту». Если n — искомое число, разделите его на все числа больше 1 и меньше 1/2n.
Первый найденный максимальный номер (с апреля 2015 года) содержит 17 425 170 цифр, или 2 57 885 161-1. Если вы не специалист, вам не стоит сидеть всю ночь, чтобы вычислить следующее число, но ElectronicFrontierFoundation — это первое простое число, состоящее не менее чем из 100 миллионов цифр, и первое простое число, состоящее не менее чем из 500 миллионов цифр.

Лучшие математические умы, а теперь и самые совершенные компьютерные программы уже давно пытаются найти закономерности в простых числах, но предсказуемых закономерностей пока не обнаружено.
Решето Эратосфена
Древнегреческий математик Евклид Александрийский, живший во втором или третьем веке до нашей эры, известен нам как первый человек, распознавший простые числа. Другой древнегреческий математик, Эратосфен, II век до н.э., ввел так называемое «решето» для поиска простых чисел. Он прост в использовании, хотя полезен только для относительно небольших чисел.
Нарисуйте таблицу с 10 столбцами и строками с числом, необходимым для соответствия проверяемому числу; если вы хотите проверить числа до n, вам нужно создать таблицу от 1 до n. Начиная с 4, прочитайте таблицу и вычеркните те, которые делятся на 2. Затем удалите числа, кратные 3, затем кратные 5, затем кратные 7 и проверьте первое число. При достижении делителя 1/2n-1 можно остановиться. Это связано с тем, что большое число не может быть делителем числа, меньшего или равного n. Числа, которые не были удалены, являются простыми числами.

Прискорбное пренебрежение
После Древней Греции простые числа мало кого интересовали до 17 века. Даже в 17 веке простые числа не использовались за пределами чистой математики, но, по крайней мере, с ними можно было играть. Они заняли достойное место в компьютерной эре с появлением необходимости разработки алгоритмов шифрования.
Пока не возникла необходимость в шифровании данных, простые числа лениво бездействовали. Сегодня, когда по Интернету ежедневно передается бесчисленное множество защищенных транзакций и других секретных данных, простые числа соответствуют безопасным путям, по которым передаются данные. Во-первых, два очень больших простых числа перемножаются, чтобы получить комплексное число.

Комплексное число используется для генерации кода, называемого открытым ключом. Этот код банк (или кто-то другой) отправляет человеку, который шифрует данные. Если вы покупаете что-то в Интернете, данные вашей кредитной карты должны быть зашифрованы с помощью этого открытого ключа. Шифрование происходит в конце строки. Зашифрованные данные представляют собой пустой набор слов, если они перехвачены во время передачи. Когда данные карты достигают другого конца, они генерируются с помощью секретного ключа — P1 и P2 -используется для расшифровки.
Это работает потому, что для больших чисел очень трудно найти первое число, от которого происходит слагаемое. Хакерам нужны 1000 лет работы компьютеров, чтобы взломать код и найти исходное простое число. Поскольку современные криптовалюты так сложно взломать, правительства предпочитают позволить разработчикам создавать «бэкдоры» в системе. Это может позволить им следить за тем, что делают люди.








