Что такое ось симметрия. Что такое ось симметрия

Транспортная симметрия — это тип симметрии, которая не изменяется при смещении свойств данной системы на определенный вектор, называемый вектором перехода. Например, однородная среда обладает специфической форовской симметрией, поскольку при смещении любого вектора она совмещается сама с собой.

Урок по теме «Симметрия в пространстве»

назад и вперед

Тип курса: комбинированный урок.

• Рассмотреть осевую, центральную и зеркальную симметрии как свойства некоторых геометрических фигур.
• Научить строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.
• Совершенствовать навыки решения задач.

Цели курса:.

• Формирование пространственных представлений учащихся.
• Развитие умения наблюдать и рассуждать; развитие интереса к предмету через использование информационных технологий.
• Воспитание человека, умеющего ценить прекрасное.

Оборудование курса:.

• Использование информационных технологий (презентация).
• Рисунки.
• Карточки с домашним заданием.

Ход урока

Введите тему урока и укажите цели урока.

Известный математик Герман Вейль высоко оценил роль симметрии в современной науке.

Мы живем в очень красивом и гармоничном мире. Нас окружают предметы, которые радуют глаз. Например, бабочки, кленовые листы и снежинки. Посмотрите, какие они красивые. Вы когда-нибудь видели их? Сегодня мы коснемся этого прекрасного математического явления — симметрии. Мы познакомимся с понятиями оси, центра и зеркальной симметрии. Вы научитесь строить и определять симметричные фигуры с осями, центрами и уровнями.

В греческом переводе слово «симметрия» звучит как «гармония». Это подразумевает красоту, пропорциональность и единообразие частей частей. С древних времен люди использовали симметрию в архитектуре. Древние храмы, башни средневековых замков и современные здания создают ощущение гармонии, наполненности.

В более общем случае «симметрия» в математике понимается как преобразование таких пространств (уровней). Это понимается как переход каждой точки ММ в другую точку относительно одного уровня (или прямой) a, в случае прямого участка mm. Она перпендикулярна уровню (или прямой) A и делится на два. Уровень (линия) A называется уровневой (или осевой) симметрией. Основные понятия симметрии включают уровень симметрии, ось симметрии и центр симметрии. Уровень симметрии P — это уровень, который делит фигуру на две равные части, которые выглядят как зеркала и расположены по отношению к одному объекту и другому так же, как его зеркальное отражение.

III. Основная часть. Виды симметрии.

Центральная симметрия.

Симметрия одной точки или центральная симметрия — это высокая геометрическая форма, если любая точка на одной стороне от центра симметрии соответствует другой точке на противоположной стороне от центра. Эти точки находятся на прямых участках, проходящих через центр и разделяющих центральный участок.

1. Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ .
2. Какие из следующих букв имеют центр симметрии: А, О, М, Х, К?
3. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?

Осевая симметрия

Симметрия относительно прямых линий (или осевая симметрия) — это геометрическая фигура, если точки по одну сторону прямой линии всегда соответствуют точкам по другую сторону линии и всегда отрезку, соединяющему их. Точка перпендикулярна оси симметрии и разделена им на два участка.

1. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
2. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О?
3. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
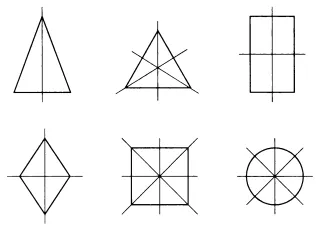
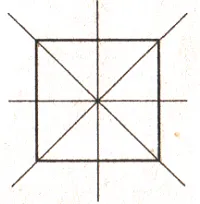
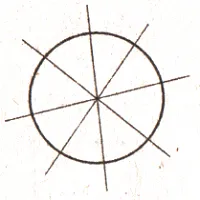
4. Сколько осей симметрии имеет рисунок? (см. рис. 1)

Рисунок 1.

Зеркальная симметрия.

Точки A и B называются симметричными относительно уровня A (уровень симметрии), если уровень A проходит через середину отрезка AB и перпендикулярен этому отрезку. Каждая часть уровня А считается симметричной сама по себе.

1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при: а) центральной симметрии относительно начала координат; б) осевой симметрии относительно координатных осей; в)зеркальной симметрии относительно координатных плоскостей.
2. В правую или левую перчатку переходит правая перчатка при зеркальной симметрии? осевой симметрии? центральной симметрии?
3. На рисунке показано, как цифра 4 отражается в двух зеркалах. Что будет видно на месте знака вопроса, если то же самое сделать с цифрой 5? (см. рис. 2)
4. На рисунке показано, как слово КЕНГУРУ отражается в двух зеркалах. Что получится, если то же самое проделать с числом 2011? (см. рис. 3)

Рисунок 2.

Рисунок 3.

Это интересно.

Симметрия живых существ.

Почти все живые существа построены по законам симметрии, что небезосновательно, ведь греческое слово «симметрия» означает «пропорция».

Например, между цветами существует вращательная симметрия. Многие цветы можно повернуть так, чтобы каждый лепесток занял положение соседнего лепестка, и цветок выровнялся сам с собой. Минимальный угол этого вращения варьируется от цветка к цветку. 120° для ирисов, 72° для колокольчиков и 60° для нарциссов.

Существует спиральная симметрия в расположении листьев на стебле растения. Спирально расположенные вдоль стебля, сами листья также имеют ось симметрии, но они расходятся в разные стороны и, кажется, не закрывают друг друга от света. Рассматривая общее строение животных, мы обычно замечаем определенные закономерности в расположении частей тела и органов. Они либо повторяются вокруг оси, либо занимают одно и то же положение по отношению к плоскости. Эта закономерность называется симметрией тела. В связи с распространенностью явлений симметрии в животном царстве, очень трудно выделить группы, в которых симметрия тела не наблюдается. И мелкие насекомые, и крупные животные симметричны.

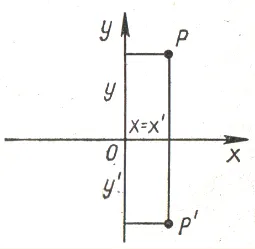
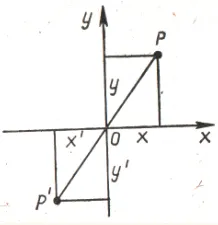
(3) При повороте на 90° вокруг начальной точки ось C превращается в ось O, а положительное направление — в положительное, ось C отражается обратно на ось C, а положительное направление меняется на a негативное направление. Таким образом, P(x, y) соответствует P’.

Центральная и осевая симметрия

Две точки в A и A₁ O симметрично вызываются относительно O, когда O является средним значением отрезка AA₁ (Фото 1). Точка O считается симметричной относительно самой себя.

Примеры центральной симметрии

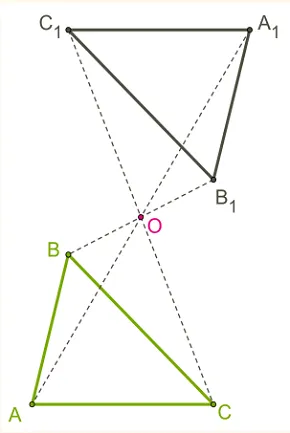
Точки А и А.₁ -симметрична относительно точки O.

Фигура называется симметричной относительно точки O, если для каждой точки фигуры существует точка симметрии относительно точки O. Точка O называется центром симметрии. Фигура также называется центрально-симметричной.

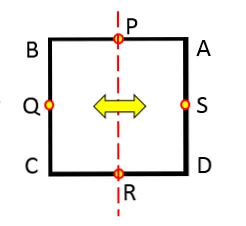
Круги и прямоугольники являются примерами центрально-симметричных фигур (рис. 2).

Структура центральной симметрии

Центром симметрии круга является центр окружности, а центром симметрии прямоугольника — пересечение его диагоналей. Линии также обладают центральной симметрией, но в отличие от круга или прямоугольника с одним центром симметрии (точка O на рис. 2), линия может иметь бесконечное число центров. Любая точка на линии является центром симметрии. A.

Осевая симметрия

Две точки в A и A₁ Если прямая проходит через центр отрезка AA, то она называется симметричной относительно прямой α₁ и перпендикулярна ему (рис. 3). Каждая точка на линии A считается симметричной относительно самой себя.

Точки А и А.₁ -симметричный под линией.

Фигура называется симметричной относительно прямой α, если для каждой точки фигуры симметрия между фигурой и прямой α также принадлежит этой фигуре. Линия a называется осью симметрии фигуры.

Пример такой формы и ее оси симметрии показан на рисунке 4.

Обратите внимание, что линия, проходящая через центр круга, является осью симметрии.

Сравнение симметрий

Центральная и осевая симметрия

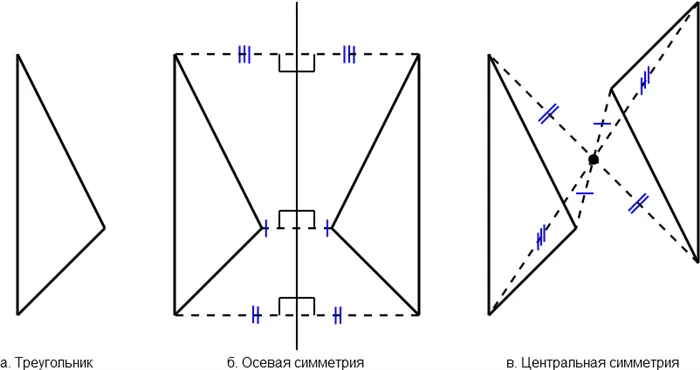
Конфигурация треугольника (a) симметрична относительно оси (b) и точки (c).

Конфигурация называется симметричной относительно прямой α, если для каждой точки диаграммы симметрия относительно прямой α также принадлежит этой конфигурации (рис. 2.2).

Уроки математики и физики для школьников и родителей

Слово «симметрия» происходит от греческого. Оно означает пропорциональность, определенный порядок и закономерность в расположении частей.

С древних времен люди использовали симметрию в дизайне, декоре, предметах быта, архитектуре, искусстве и структуре.

Симметрия присуща всем, где не было вмешательства человеческой руки. Его можно увидеть в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающих бабочках, загадочных снежинках и хлопающих крыльями морских звездах.

Две точки, расположенные на одной вертикали (или прямой) по разные стороны (или прямой) и на одинаковом расстоянии от нее, называются симметричными относительно уровня (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой линии (симметричный вал) или уровня (симметричный уровень), если точки пары обладают этой характеристикой.

Две точки A и B симметричны относительно прямой (симметричный вал), если эта прямая проходит через центр отрезка AB и перпендикулярна ему.

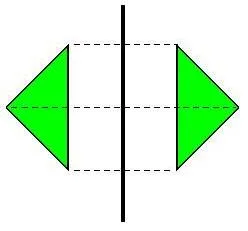
Для каждой точки фигуры, если точка симметрии прямой принадлежит этой фигуре, то фигура симметрична относительно прямой.

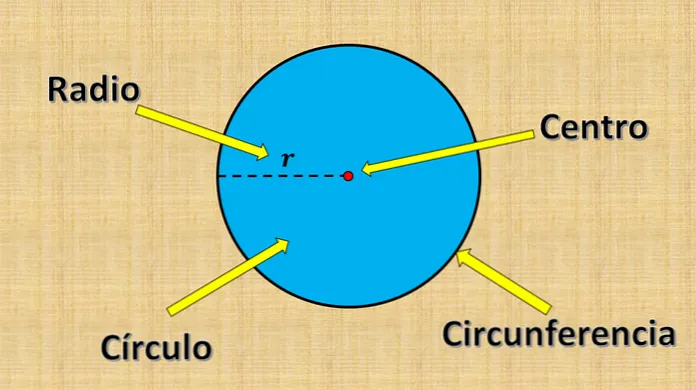
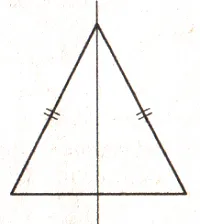
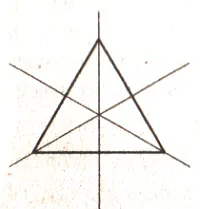
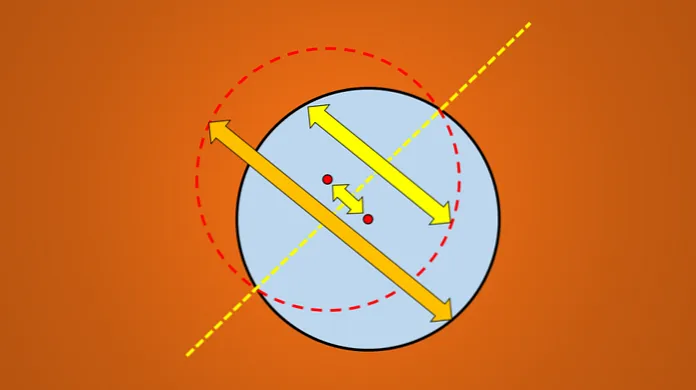
Цикл имеет бесконечное число осей симметрии — каждая линия, проходящая через центр, является симметричной осью.

Прямоугольники и треугольники являются примерами несимметричных фигур.

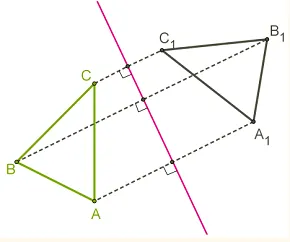
Построим треугольник. a₁ В₁ Больше.₁ , треугольники ABC и симметрия в терминах красных линий (симметричные валы).

Уроки математики и физики (RU + UA)

• I. НАТУРАЛЬНЫЕ ЧИСЛА И ДРОБИ (RU + UA + EN)
• II. ПРОПОРЦИИ ПРОЦЕНТЫ МАСШТАБ (RU + UA)
• III. РАЦИОНАЛЬНЫЕ ЧИСЛА (RU + UA)
• IV. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ (RU + UA)
• V. КОРНИ (RU + UA)
• VI. ФУНКЦИИ И ГРАФИКИ (RU + UA + EN)
• VII. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ (RU + UA)
• VIII. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
• IX. НЕРАВЕНСТВА (RU + UA)
• X. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (RU + UA)
• XI. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА (RU + UA)
• XII. ПЛАНИМЕТРИЯ (1) (RU + UA)
• XIII. ПЛАНИМЕТРИЯ (площади фигур) (RU + UA)
• XIV. СТЕРЕОМЕТРИЯ (1) (RU + UA)
• XV. СТЕРЕОМЕТРИЯ (2) (RU + UA)
• XVI. КОМБИНАТОРИКА (RU + UA)
• XVII. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ (RU + UA)
• XVIII. ВЕКТОРЫ (RU + UA)
• XIX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ (RU + UA)
• XX. ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (RU + UA)
• КИНЕМАТИКА
• ДИНАМИКА
• WATCH YOUR MONEY!

Сайт содержит минимум математической информации, так что каждый студент может сдать тест с положительной степенью, если решит все рекомендованные курсы естественным образом. Сайт также полезен для студентов, которые начинают изучать математику или хотят помочь своим внукам в изучении математики.

Каждый урок содержит краткую информацию по теоретической части и три практических упражнения с 12 примерами или задачами по каждому заданию. При необходимости учащиеся могут присылать свои ответы на упражнения для просмотра в разделе комментариев. Сайт постоянно совершенствуется. Возможны методологические и математические ошибки.

В биологии все виды называются немного разными, но по сути могут быть одинаковыми. Разделение их или их групп основано на наличии или отсутствии и на ряде специфических элементов, таких как центры симметрии, уровни, оси и т.д. Их необходимо рассмотреть по отдельности и более подробно.

Осевая и центральная симметрия — сообщение доклад (6, 8 класс)

Симметрия — неотъемлемая часть мира, в котором мы живем. Мы восхищаемся красотой природы, архитектурных сооружений, механических устройств и шедевров искусства, специально не рассматривая симметрию как основу их создания.

Греческое слово «симметрия» переводится как гармония, пропорция и красота. Впервые этот термин был широко использован Пифагором. Пифагор определил трехмерное представление геометрической фигуры и части ее пространства. Ученый также определил отклонение от симметрии как асимметрию.

Существует два основных типа симметрии: осевая симметрия и центральная симметрия.

Осевая или зеркальная симметрия — это симметрия вокруг оси. Это означает, что половина фигур идеально пропорциональна другой половине, относящейся к прямой линии. Таким образом, когда лист сгибается к центру, каждая половина листа имеет двойника в другой половине, а само складывание становится симметричным валом.

Зеркальная симметрия встречается в природе. Листья растений симметричны относительно середины стебля, крылья бабочек похожи друг на друга, а у людей и животных есть симметрия в расположении частей тела. Архитектурные сооружения — еще один классический пример осевой симметрии. Фасады зданий, особенно старинных, вызывают чувство строгости и восхищение красотой из-за симметрии их частей. Архитектурная симметрия не только доставляет эстетическое удовольствие наблюдателю, но и обеспечивает долговечность и прочность зданий и сооружений.

Центральная симметрия — это симметрия относительно точки. Эта симметрия обязательно имеет фиксированный центр, который может быть перенесен на себя поворотом на 180° вокруг него. Благодаря этому свойству центральная симметрия получила второе название — поворотная. Он давно считается круговым узором, и хотя он не вращается вокруг центра, каждая точка круга соответствует ему. В природе яркими примерами центральной симметрии являются цветки таких растений, как снегири, одуванчики, мать-и-мачеха, ромашка, которая представляет собой механизм шестеренки, если число лепестков четное.

Вариант 2

Наверное, каждый слышал о таких понятиях, как «симметрия» и «симметричность». Однако некоторые люди не понимают, что означают эти синонимы. Так что же такое симметрия? Применение; и какие существуют вариации?

Краткая справка о симметрии в целом.

Я попытаюсь объяснить концепцию симметрии на примере. Представьте себе обычную бабочку. Теперь вам нужно провести через него линию. После того как вы окончательно провели линию, необходимо посмотреть на правую и левую стороны рисунка. Если эти две части дизайна одинакового размера и в одинаковой пропорции, то дизайн можно назвать симметричной моделью. По сути, симметрия — это идеальная пропорциональность частей тела по отношению к линии. Так где же применяется симметрия? Ну, симметрия — это то, где вы можете ее найти. Геометрия, физика, биология, химия, культура — все они связаны с симметрией, и каждая из них по-своему уникальна. Существует также понятие асимметрии. То есть, отсутствие надлежащей пропорциональности. Также обратите внимание, что симметрия не всегда является точной.

Несколько типов симметрии, их свойства и применение.

Существует приблизительно 12 типов симметрии. Однако необходимо рассмотреть только те, которые часто встречаются. Заметим сразу, что и то, и другое относится к геометрическим задачам. Двумя основными типами симметрии являются

Осевая симметрия.

Этот тип симметрии можно разделить на четыре группы, которые отличаются друг от друга.

(1) Рефлекторная симметрия — это зеркальное движение, при котором точки, которые никуда не перемещаются, соединяются линиями, осью симметрии которых является ось симметрии. Прямоугольники и прямоугольники — отличные примеры.

2) Вращательная симметрия — это осевая симметрия, связанная с вращением вокруг оси.

(3) Осевая симметрия n-го порядка — это симметрия относительно вращения на 360° вокруг оси.

4) Зеркальная вращательная симметрия оси n-го порядка такая же, только перпендикулярна оси.

Центральная симметрия.

Это такое преобразование, когда каждая точка A проходит через точку A1 и симметрична относительно предыдущей точки относительно оси O. Эта симметрия фактически совпадает с поворотом планетарного измерения на 180°. Центральная симметрия отличается от осевой симметрии тем, что в первом случае есть движение.

Картинка к сообщению Осевая и центральная симметрия

Исаак Эммануилович Бабель (также известный как Бобел) родился в еврейской семье в Одессе. Он стал известным писателем, драматургом, сценаристом и журналистом.

Пружеварский Николай Михайлович был известным русским географом, путешественником и физиком, внесшим значительный вклад в изучение географии и топографии Азии, особенно территорий Китая, Марокко, России и Украины.

Этот выпуск является ранним источником информации, объясняющим историю России. В нем содержится информация о Средних веках. Это повествование, которое помогает современным ученым реконструировать события 20-го века.

Фернандо Магеллан (1480-1521) родился в небольшой португальской дворянской семье. Свой первый крупный морской поход он совершил в 1505 году.

Северный Ледовитый океан глубже и больше, чем все океаны на нашей планете. Его территория находится в северном полушарии нашей планеты и

Бельгия, или Королевство Бельгия, — страна в Западной Европе. На севере она граничит с Нидерландами, на востоке и юго-востоке — с Германией, а во Франции — с Люксембургом.