Новые телевизоры становятся еще более удобными в использовании, и больше нет необходимости подключать дополнительное внешнее оборудование для отслеживания кабельных или спутниковых каналов. Задача приемника, встроенного в ресивер, заключается в приеме доступных потоков в различных форматах и декодировании сигналов.
Что такое модуль?
Термин «единство» — очень новое понятие в современном российском образовании. Конечно, родители слышат его впервые, но опытные люди и учителя знают, что стоит за этим словом: термин «объединение» — новое понятие в российском образовании.
Секции являются частью учебных программ, в которых изучаются различные предметы и уроки. Часто раздел является частью программы курса, набора тем или курса по определенной научной дисциплине.
Основное отличие позвоночной и традиционной ветвей образования заключается в самостоятельной работе студента. Студент изучает предмет, а профессор координирует и контролирует его деятельность, организует учебный процесс, консультирует и мотивирует студента. Новая информация преподается в виде блоков, в которых изучаются конкретные педагогические цели. Форма общения между преподавателем и студентом также отличается от традиционных форм обучения. У студентов есть индивидуальные учебные карьеры.
Разделы современного российского образования включают
Часть образовательной программы
Основа для разработки новой учебной программы.
Основа для модернизации курсов повышения квалификации.
Структура модульного обучения
Учебный процесс с позвоночными формами обучения строится на основе учебного плана, утвержденного Министерством образования и науки Российской Федерации.
Структура образовательной программы включает в себя различные модули. Реализация модулей представлена блоками. Кредитная единица включает 36 академических часов. За учебный год студенты должны пройти 60 кредитных единиц. Кредитная работа подразделяется на
Практические и лабораторные работы,.
Консультирование, тестирование и обучение.
Каждый раздел состоит из учебных данных (обычно от пяти до восьми элементов в одном разделе), состоящих из целей, материалов, списка СПИДа и теста приобретенных знаний.
В данных об обучении есть различия.
Основной элемент вопрос (дело), вопрос
Цель программы Learning Spinal Animals — организация и проведение учебного процесса, основанного на принципах самостоятельной работы студентов, повышение эффективности и качества обучения и развитие гибких профессиональных компетенций. Модули разработаны таким образом, чтобы ребенок мог понять все стоящие перед ним задачи, получить необходимую информацию и успешно усвоить материал.
Полученные знания оцениваются с помощью системы оценки.

Широко распространены методики раннего развития детей, разработанные Марией Монтессори. Согласно ее методике, каждый ребенок индивидуален. Им необходимо развиваться и учиться в свободном пространстве, при поддержке любимого взрослого. Цель книги — не только показать различия между группами детского сада и школы, но и рассказать о потенциале начальных школ с системой Монтессори и перспективах роста в нашей стране.
Модульная система обучения
Позвоночная система обучения действует в форме Европейской системы перевода кредитов (Болонская система, ECTS), основанной на объеме учебной нагрузки.
Модульное обучение основано на модульной (блочной) структуре учебных материалов и оценивается суммой баллов за различные виды деятельности. Учителя самостоятельно определяют количество оценок и виды учебной деятельности, соответствующие каждой единице.
Два шарика катятся по прямой линии. Первый шар катится на 4 м вправо от начальной точки, а второй шар — на 6 м влево от начальной точки.
Геометрическое значение
Если рассматривать понятие коэффициента с точки зрения геометрии, то он обозначает расстояние, измеренное в единичных отрезках от начала до заданной точки. Это определение делает совершенно понятным среднее геометрическое исследуемого термина.

- Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
- Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.
График можно выразить следующим образом. = OA.
Свойства абсолютной величины
Все математические свойства термина и то, как он может быть записан в виде формулы, объяснены ниже.

- Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0 .
- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а| .
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0| .
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В| .
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | | .
- Такое же правило распространяется и на показатель степени выражения.
Особенности решения уравнений с модулем

Говоря о решении формул и неравенств с единицами, следует помнить, что их решение требует нахождения этой точки.
Например, если знак абсолютной величины содержит формулу, то перед тем, как раскрыть единицы измерения, необходимо рассмотреть соответствующее математическое определение.
| A + 5 | = A + 5, если A больше или равно нулю.
5 — A, если A меньше нуля.
В некоторых случаях знак может быть четко раскрыт для любого значения переменной.
Давайте рассмотрим другой пример. Создадим координатную линию, на которой отмечены все числа, абсолютное значение которых равно 5.
Сначала нужно провести линию координат, отметить в ней начало координат и определить размеры единичного отрезка. Линия также должна иметь направление. Затем на этой линии нужно нарисовать отметку, равную размеру единичного отрезка.
Таким образом, мы видим, что эта координатная линия имеет две интересующие нас точки со значениями 5 и -5.
В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символическую нотацию для числовых коэффициентов, которая используется и по сей день.
Свойства модуля (абсолютной величины)
Давайте рассмотрим некоторые свойства числовых коэффициентов.
1. абсолютное значение числа равно нулю
Измерение нуля равно нулю, потому что не существует расстояния от нуля до первого (нулевой единичный отрезок).
2. абсолютное значение числа всегда является неотрицательным числом (т.е. положительным или нулевым)
По определению, модуль равен расстоянию, а расстояние всегда является положительным числом, поэтому модуль положителен.
Мяч катится на 3 м вправо по прямой, ударяется о стену, катится на 3 м в обратном направлении и останавливается.
Координаты точки строятся в момент остановки шарика на координатной прямой.

Точка O на координатной прямой — это точка, в которую скатился мяч, т.е. начальная точка.
Единицами измерения координатной линии является 1 масштаб — 1 метр.
Точка A с координатой A (+ 3) — это момент удара мяча о стену.
Точка B с координатой B (0) совпадает с точкой B — начальной точкой.
Можно ли сказать, что мяч оказался в точке 0 м (от точки 0 до начальной точки О не совпадает ни одна единичная часть), значит, в начале он был спокоен и не прошел никакого расстояния? Ни в коем случае!
Если он вообще не бил и был спокоен в точке O, то путь мяча был нулевым.
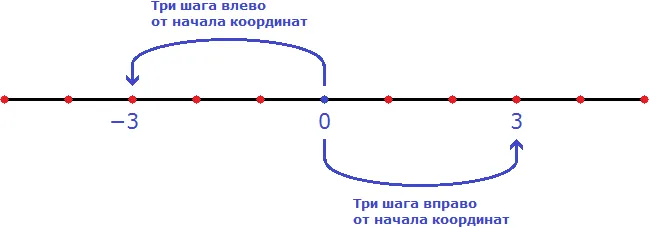
Однако следует понимать, что путь (расстояние), пройденный мячом, состоит из трех единичных отрезков вправо и трех влево. Это означает, что сумма всех единичных отрезков будет следующей
3 единичные части + 3 единичные части = 6 единичных частей
6 отрезков линии = 6 м
Для определения расстояния добавлены только числовые значения, не включая направление. Это арифметическое значение является коэффициентом числа.
Поэтому можно сказать, что каждое число состоит из знака и абсолютного значения (единицы).
Поэтому, чтобы найти коэффициент числа, нужно описать число, не учитывая его знак.
Более подробная информация об этой части курса!

В математике был придуман шуточный смысл, чтобы сделать тему «абсолютное значение числа» более понятной.
Представьте, что модуль — это ванна, а минус — грязь.
Когда вы входите в ванну (под символом платы), отрицательное число смывается и освобождается символом. Числа выходят из ванны (под знаком цены) «чистыми» — без знака минус.
В этой ванне можно «мыть» положительные, отрицательные и нулевые числа.
Числители противоположных чисел равны.
Рассмотрим это утверждение в качестве примера.
Если коэффициент x равен 4, то уравнение| x | = 4
Обратите внимание, что координатная линия удовлетворяет этому уравнению.
Решение задач с применением модуля числа
Давайте рассмотрим несколько примеров таких проблем.
Запишите все числа, коэффициенты которых равны 142.
Выразите координатную прямую, начинающуюся в точке O.
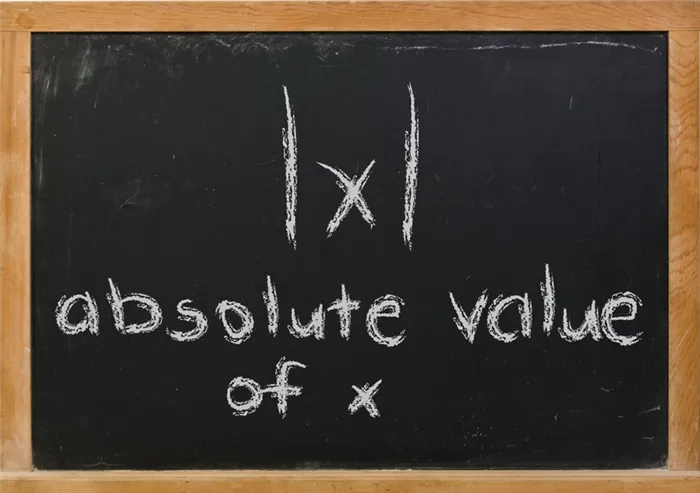
Мы знаем, что мера числа — это расстояние от нуля до точки (количество единиц).
Используя шаг 142d, мы можем получить точку с координатами 142 на правильной координатной прямой.
Вы также получите точку с координатами 142, так как слева от нуля можно разместить 142 единичных отрезка.
Координатная прямая содержит два числа с законом 142, а расстояния от этих точек содержат единичный отрезок 142.
ОТВЕТ: числа 142 и -142 имеют закон 142.
Разложите числа -15? -1; 4; 7 по модулю.
Следует понимать, что числа расположены не в порядке возрастания — 15? -1; 4; 7, а их разделы.
Для этого найдите каждый раздел.
Числа в единицах 15, 1, 4 и 7.
Расположите эти числа в порядке возрастания (от наименьшего к наибольшему).
1, 4, 7, 15.
Получите эту серию уравнений.
Таким образом, возрастающие номера единиц должны быть -1, 4, 7 и -15.
Ответ: -1, 4, 7, -15.
Обратите внимание на координатные линии -73 и 68. Какой элемент числа больше?
Представьте, что на координатной прямой отмечены две точки на определенном расстоянии от точки O (начальная точка).
Слева от первой находится точка с координатой -73.
На правой стороне первой из них координата равна 68.
Модуль — это расстояние от определенной точки до начальной точки, выраженное в долях единицы.

Расстояние от точки О до координаты -73 содержит больше единичных отрезков, чем расстояние от точки О до координаты 68 (т.е. координата -73 находится дальше от начальной точки, чем координата 68).
Следовательно, модуль упругости -73 больше, чем модуль упругости 68
73> 68, т.е.
Ответ:| -73 | > | 68 |
На координатной прямой точка A отмечена на 2 единицы влево от начальной точки, а точка B — на 6 единиц вправо от начальной точки.
Каковы координаты этих точек?
Каковы коэффициенты каждой координаты?
Построение прямых координат и доставка от точки к точке
В этой записи первая конвенция, которая ранее выглядела как x ≥ 0, представлена более подробно. То есть для x > 0 он равен выражению | x | x, а для x = 0 он равен выражению x | zero.
Обобщённое понятие модуля числа
В этом курсе подробно объясняется понятие коэффициентов чисел.
Модуль упругости — это расстояние от начала до определенного количества координатных линий. Поскольку расстояние никогда не бывает отрицательным, модуль всегда неотрицателен. Таким образом, мера 3 равна 3, так же как мера -3 равна 3.
В координатной прямой мы предполагаем, что расстояние между целыми числами равно одному шагу. Теперь, если мы запишем числа -3 и 3, расстояние от начала равно трем шагам.
Фактором является не только расстояние от начала до числа. Модулем также является расстояние между двумя числами на координатной прямой. Это расстояние выражается с помощью символов измеренных значений как разница между этими числами.
Где x1 и х2 — Это номера координатной линии.
Например, отметьте на координатной прямой цифры 2 и 5.
![]()
Расстояние между числами 2 и 5 можно описать с помощью коэффициентов. Для этого опишите разницу между числами 2 и 5 и поместите эту разницу под символом Modulo.
Вы увидите, что расстояние от номера 2 до номера 5 составляет три шага.

Если расстояние от 2 до 5 равно 3, то расстояние от 5 до 2 также равно 3.

Другими словами, если мы поменяем местами числа в уравнении| 5-2 | результат останется тем же.
Тогда мы можем записать| 2-5 | = | 5-2 |. В общем случае применяется следующее уравнение.
Это уравнение можно прочитать следующим образом: расстояние от x1 к х2 равно расстоянию от x2 к х1| 3 | = 3 или | -3 | = 3, мы выполняем действие, называемое факториальным расширением.
Раскрытие модуля
Правило расширения коэффициента выглядит следующим образом
Это примечание мы не использовали в прошлом. Дело в том, что вы можете давать разные виды равенства. Скобка предполагает, что возможны два случая, в зависимости от ситуации. В этом случае условиями являются «x ≥ 0» и «если x 0».
В зависимости от того, что заменяется на x, выражение x | равно x, если заменяемое число больше или равно нулю. Если x заменить на число, меньшее нуля, то x | будет равно -x.
Во втором случае, как символизм, на первый взгляд может показаться противоречивым, что x | = -x по модулю кажется равным отрицательному числу. Обратите внимание, что если x равен нулю, то под знаком множителя стоит отрицательное число. После знака равенства замените x на это отрицательное число и раскройте скобку.
Например, используйте правило разложения по модулю, чтобы найти его коэффициент -7.
В этом случае второе условие x
Поэтому используйте второй тип. Это x | | = -x. Добавьте -7 вместо x.< 0, ведь −7 < 0
Пример 2. Предположим, что x = 5. То есть, рассмотрим фактор 5
В этом случае первое условие x ≥ 0 применимо для 5 ≥ 0.
Поэтому мы используем первый тип. То есть, x | = x. Принимаем 5 = 5.
Ноль — это своего рода точка перехода, в которой Unity меняет порядок развития и сохраняет свою подпись. Визуально это можно представить следующим образом.
На диаграмме красные символы минус и плюс обозначают отрезки| x | расширяются на интервал x
Например, если вы получите числа 1, 9 и 13 и они принадлежат x≥0, то диаграмма расширится с помощью символа section| x | плюс:.< 0 и x ≥ 0 .
Также, если взять числа меньше нуля, например, -3, -9, -15, то, согласно диаграмме, отрезок расширяется со знаком минус.
Пример 3. x =√4 — т.е. рассмотрим коэффициент выражения √4-6.
Корень из 4 равен 2. В этом случае фактор
x, который был √4-6, теперь равен -4. В этом случае второе условие x
Поэтому используйте второй тип x | = -x. Продолжите решение исходного примера.< 0, ведь −4 < 0
Коэффициенты в уравнении можно рассматривать как полные множители. Их можно уменьшать и снимать со скобок. Если модуль является частью полинома, его можно добавить к аналогичному модулю.
Преобразование выражений с модулями
Как и обычные буквенные множители, модуляр имеет свои коэффициенты. Например, модуль отрезка x | 1 и модуль отрезка — | x | -1. Коэффициент отрезка 3| x +1 | равен 3, а коэффициент отрезка -3| x +1 | -3.
Пример 1. Упрощение выражения x | + 2 | x | -2 x + 5 y и выявление коэффициента выражения результата.
Выражения x | и 2 x | являются аналогичными понятиями. Сопрягайте их. Остальное оставьте без изменений:.
Разработайте факторы исхода. Для x ≥ 0 имеем 3 x -2 x + 5 y, где x + 5 y.
Если x
существует следующее решение.< 0, то получим − 3 x − 2 x + 5 y , откуда − 5 x + 5 y . Вынесем за скобки множитель − 5, получим − 5( x − y )
Пример 2. Развить его коэффициент — | x |
В этом случае перед символом коэффициента ставится минус. Его можно воспринимать как минус перед символом modulo. Если x ≥ 0, то модуляция происходит через символ плюс, и исходное выражение становится -x
Монтессори.








