Длина множества — это число n его компонентов. Множество, состоящее из компонентов в этом порядке, обозначается. В этом случае i i i i () является компонентой множества.
Множества и операции над множествами
В математике понятие множества является одним из основных, фундаментальных, но не единых определений. множества не существует. Одно из самых распространенных определений множества является следующее: под множеством это любая совокупность определенных и отличных друг от друга объектов, рассматриваемых как множество. Создатель теории множеств немецкий математик Георг Кантор (1845-1918) сказал. так»Множество — это количество, которое мы рассматриваем как единое целое».
Вы сегодня обедали? Я открою вам страшную тайну. Обед множеством. А именно, множеством Блюдо, из которого оно состоит. В нем (как правило) нет двух одинаковых блюд, и во множестве все элементы должны быть разными. И если вы съели на обед тот же салат, что и на завтрак, то этот салат — гибрид из множеств «Обед» и «Завтрак».
Посмотрите на книгу на столе или на полке. Это множеством страницы. Все страницы отличаются друг от друга, по крайней мере, по количеству.
А улица, на которой вы живете? Это собрание множества различных объектов, но обязательно есть множество домов, которые находятся на этой улице. Вот почему множество домов является подмножеством множества «Улица».
Итак, мы не только рассмотрели примеры множеств, но и пример функции над множествами — пересечение, а также интеграционные отношения в контекстемножества во множество. Все эти понятия будут подробно рассмотрены в этом уроке.
А пока вот еще один пример, который нам следует рассмотреть на практике. множеств.
Наборы как тип данных оказались очень полезными при программировании сложных жизненных ситуаций, так поскольку они могут быть использованы для точного моделирования объектов реального мира и компактного представления сложных логических отношений. Наборы используются в языке программирования Pascal, и ниже представлен пример решения.
Пример 0 (Паскаль). Существует набор продуктов, продающихся в различных магазинах города. Определите: какие товары присутствуют во всех магазинах города; общий ассортимент товаров в городе.
Решение. Определите базовый тип данных о продуктах питания, который может принимать значения, соответствующие названиям продуктов (например, hleb). Объявление тип множества, определяет все подмножества, из комбинаций значений базового типа, т.е. продуктов питания. И мы образуем подгруппумножестваСолнышко, Веторок, Огонек, а также производные подмножестваMinFood (продукты, доступные во всех магазинах), MaxFood (весь ассортимент продуктов в городе). Затем напишем операции для получения производных примножеств. Подмножество MinFood — это результат пересечения подкатегорий.множеств Солнышко, Ветерок и Огонек и включает эти и только эти элементы этих подгруппмножеств, которые содержатся в каждой из этих подгруппмножеств (в Паскале операция пересечения множеств отмечен звездочкой. C, математическУсловное обозначение пересечения множеств дано далее). Подмножество MaxFood получается путем комбинирования одного и того же субмножеств и включает элементы, которые содержатся во всех подмножества (в Паскале операция объединения множеств A + B + обозначается знаком плюс. C, математическУсловное обозначение союза множеств дано далее).
Код PASCAL
program Shops; type Food=(hleb, moloko, myaso, syr, sol, sahar, maslo, ryba); Shop = set of Food; var Solnyshko, Veterok, Ogonyok, MinFood, MaxFood: Shop; Begin Solnyshko: =хлеб, молоко; Ветерок:=хлеб, сир, масло; Огонек:=хлеб, мясо, рыба, сол, сахар; МинПитание:=Солнышко * Ветерок * Огонек- МаксПитание:=Солнышко + Ветерок + Огонек- Конец.
Какие бывают множества
Объекты, из которых множества — Объекты нашей интуиции или интеллекта — могут иметь совершенно иную природу. Пример в первом абзаце касался множества, которая включает в себя ряд продуктов. Предложения, например, могут состоять из всех букв русского алфавита. В математике изучаются множества чисел, например, состоящий из всех
— натуральные числа 0, 1, 2, 3, 4, .
— чётные целые числа
(Основные арифметические действия множества рассматриваются в соответствующем разделе данного материала).
Объекты, из которых множество, называются его элементами. Вы можете сказать это, что множество — это «мешок с уликами». Это очень важно: в множестве нет двух одинаковых элементов.
Существуют конечные и бесконечные множества. Finite множество — это множество, для которых существует натуральное число, являющееся числом их элементов. Например, множество первые пять неотрицательных нечетных чисел конечны. множеством. Множество, которое не является конечным, называется бесконечным. Например, множество всех положительных целых чисел конечна множеством.
Если M — множество, и a является его элементом, мы пишем: a ∈ M, что означает «a принадлежит множеству M «.
Начиная с первого (нулевого) примера на языке Pascal с продуктами, доступными в некоторых магазинах:
что означает: элемент «hleb» принадлежит множеству товаров, представленных в магазине «Ветерок».
Существует два основных способа указания множеств: количество и описание.
Множество может быть определено, например, путем перечисления всех элементов:
Только конечный элемент может быть определен как перечисление. множество. Но мы также можем сделать это с помощью описания. Но бесконечный множества может быть определена только описанием.
Для описания множеств Используется следующий метод. Пусть p ( x ) — это высказывание, описывающее свойства переменной x, диапазон значений которой равен множество M . Тогда через M = x | p ( x )> обозначаентся множество, состоящий из всех и только тех элементов, для которых утверждение p ( x ) истинно. Выражение выглядит следующим образом так: «Множество M, состоящее из всех таких x, что p ( x ) «.
означает множество Корни уравнения x І — 3 x + 2 = 0, t. е. множество. Это конечное множество.
И следующее описание дается множество всех целых чисел больше 5:
это множество это бесконечность.
Предпочтительно, чтобы описание было также конечным множества, которые имеют много элементов, например множество все натуральные числа от 2 до 22³ :
Множество, не содержащее элементов, называется пустым и обозначается ∅.
Множество может состоять из одного элемента. Необходимо различать элемент a и множество a > которая содержит только один элемент a, только потому, что она допустима множества, элементы, сами элементы которых множествами. Например, множество a = состоит из двух элементов 2 и 1, а множество a > состоит из элемента a, который сам является димерным элементом множеством.
Два множества считаются равными, если они состоят из одинаковых элементов. Например, равный множество равносторонние треугольники и множество Равносторонние треугольники, так как это одни и те же треугольники: если в треугольнике все стороны равны, то равны и все его углы. Обратно, из равенства всех трёх углов треугольника вытекает равенство всех трёх его сторон. Равны любые два конечных множетсва, отличающиеся друг от друга только лишь порядком их элементов, например, a, b, c > = c, a, b > .
Подмножества
Каждый квадрат является правильным треугольником. Из этого следует, что, что множество …квадраты являются частью… множества …прямоугольников, или, как они говорят…. в математике, является подмножеством множества прямоугольников.
Содержимым является множество A в множество B (символическая нотация), если какой-либо элемент. множества А принажлежит множеству В . В этом случае множество А является подмножеством множества В .
Если и, написано и сказано, что множество А строго включено в множество B или что A является собственным значением примножество В .
Например, если и, то A является собственным значением примножество В .
Верно следующее утверждение: пустой множество есть подмножество любого множества, то есть для любого множества А
Если множество содержит не менее двух элементов, имеет все возможные подэлементымножества, под которыми находятся электронные элементымножества.
Например, все возможные подмножества множества это
среди них и является уникальной частьюмножества множества .
Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается .
Например, если, то, то все возможные элементы, которые имеют уникальную идентичность, являются всеми элементами, которые имеют уникальную идентичность.
Теорема о мощности множества степени:
Вот пример практического применения этого понятия множеств — подмножества — в теории игр: с помощью подмножеств формирование коалиций и изучение того, выгодно ли акторам (особенно в компаниях) участвовать в коалициях для достижения общих целей.
Решить задачу на множества самостоятельно, а затем посмотреть решение
Пример 3. Сколько элементов они содержат? множество
В приведенном выше примере симметричная разность аналогична нахождению соответствующего дополнения множества X и множества Y. Если мы посмотрим на это с точки зрения математики, найти симметричное различие — это то же самое, что объединить относительные дополнения множества X и множества Y. Функция может быть записана следующим образом такX △ Y= (X ∖ Y) ∪ (Y ∖ X).
Содержание
До XIX века математиками в основном рассматривались конечные множества.
Основы теории конечного и бесконечного множеств была заложена Бернардом Больцано, который также сформулировал некоторые из ее принципов.
Между 1872 и 1897 годами (в основном 1872-1884) Георг Кантор опубликовал серию трактатов, в которых он систематически изложил наиболее важные части теории множеств, включая теорию точек. множеств и теория трансцендентных чисел (кардинальных и порядковых). В этих работах он не только представил фундаментальные понятия теории множеств, но и обогатил математику силлогизмами нового типа, которые он использовал для доказательства теорем из множеств, в частности, впервые в бесконечном множествам. Поэтому общепризнанно, что теория множеств создал Георг Кантор.
В частности, Георг Кантор определил множество как «единое имя для множества всех объектов, обладающих определенным свойством». Эти объекты называются элементами. множества. Множество объектов, обладающих свойством » width=»» height=»» />. Если некоторое множество , то .
Это понятие привело к парадоксам, в частности к парадоксу Рассела.
Так как теория множеств используется как основа и язык для всех современных математическВ 1908 году теория теорий, теория множеств была аксиоматизирована независимо друг от друга Бертраном Расселом и Эрнстом Цермело. Впоследствии многие исследователи пересмотрели и модифицировали обе системы, в значительной степени сохранив их характер. По сей день они известны как теория типов Рассела и теория Цермело. множеств Теория Цермело. Сегодня теория Кантора множеств Теория Кантора называется наивной теорией множеств и новая аксиоматическая теория множеств .
На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело-Френкеля с аксиомой выбора). При таком подходе в некоторых математическИх теории приводят к наборам объектов, которые не являются множествами. Такие множества называются классами (различных классов).
Элемент множества
Объекты, которые удовлетворяют множество, называются элементами. множества или точками множества. Множества обычно обозначаются прописными буквами латинского алфавита, а их элементы — строчными буквами. Если a является элементом множества A, то пишем a ∈ A (a принадлежит A). Если a не является элементом множества A, то напишите a ∉ A (a не принадлежит A).множества каждый элемент множества уникален, и в множестве не может быть двух одинаковых элементов. Другими словами, добавив к множеству элементы, идентичные тем, которые уже принадлежат множеству, не меняет этого: = = .
Специальные множества
-
— множество, который не содержит никаких элементов. (Вселенная) — множество, которая содержит все ментальные объекты. В связи с парадоксом Рассела этот термин теперь интерпретируется как » «.множество, включающее все множества, которые имеют отношение к рассматриваемой проблеме». — множество, В котором дано отношение порядка.
Сходные объекты
-
(в частности, упорядоченная пара) — это множество с конечным числом номинальных объектов. Он пишется в круглых скобках, и спецификации могут повторяться. — множество с кратными элементами.
- Пространство — множество Элемент линейного пространства, содержащий конечное число элементов поля в качестве координат. Порядок имеет значение, и элементы могут повторяться — функция одной физической переменной. Он представлен в виде бесконечного множества (не обязательно дискретных) элементов, порядок которых имеет значение. — математическОбъект, который определяется множество, которая является не отношением, а функцией. Другими словами, с точки зрения элементов этих множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.
По иерархии
См. также
- ↑ Русский перевод — Кантор Г. Труды по теории множеств. — М .: Наука, 1985. — С. 173.. Немецкий оригинал — Georg Cantor. Beiträge zur Begründung der transfiniten Mengenlehre (нем.) // Mathematische Annalen. — 1895. — Т. 46. — С. 481.
Логические операции над понятиями.
Выражение — это конструкция над множеством В — непустое множество, на элементах которого определены три операции: Конъюнкция (,бинарный); отрицание (
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Множество» в других словарях:
ЧИСЛО — см. класс в Logic. Философский энциклопедический словарь. Москва: Советская энциклопедия. Главные редакторы: Л. Ф. Ильичев, П. Н. Федосеев, С. М. Ковалев, В. Г. Панов. 1983. разнообразие … Философская энциклопедия
множество — См. excess, much, abundance much. множество. Словарь русских синонимов и сходных выражений. под редакцией Н. Абрамова, М.: Русские словари, 1999. множество Избыток, много, изобилие, изобилие, масса, изобилие, бездна, бездна, бездна, бездна, куча, куча, куча. Словарь синонимов
множество — набор — http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=4318 множество Одна из основных концепций современного математики, «произвольное собрание определенных и отдельных объектов, мысленно сформированных в единое… …. Руководство для технических переводчиков
Набор — Набор одна из основных концепций современного математики, «произвольное множество определенных и различимых объектов, мысленно объединенных в единое целое». (Таким образом, определяется множество основатель теории множеств, известный немецкий …. …. экономическийматематический словарь
УМНОЖЕНИЕ, множества, см. 1. только версия. Неопределенно большое количество; количество чего-либо. Ряд работников. Разнообразные мероприятия. «Я слышал в своей жизни множество величайших певцов». Некрасов. 2. набор элементов, которые можно найти в… …словарь Ушакова.
LOTS — LOTS, multiply, etc. см. много. Словарь Даля. В.И. Даль. 1863 1866… Словарь Даля
ЛОСС. это множество, совокупность, коллекция и т.д. объектов, называемых их элементами и имеющих одну общую для всех характеристику. Термин М. относится к группе оригинальных математических терминов и может быть объяснен только на примерах. Таким образом, кратность…. Энциклопедия физики.
множество — МНОГО, изобилие, лавина, море, полнота, наводнение, пропасть, вагон, телега, куча, масса, бездна, пропасть, пропасть, пропасть, тьма, тьма. Унция, утимища, разговорный…. Словарь синонимов русского языка
Набор — совокупность элементов, параметров, объединенных каким-либо признаком Словарь бизнес терминов. Academics.ru. 2001 … Словарь бизнес-терминов
МНОЖЕСТВО — в математике, См. Теория множественности … Большой энциклопедический словарь
LOTS — A LOT, a, ср. 1. очень большое количество; ряд. М. людей. М. дела. Все виды акций. во множестве. 2. В математике: совокупность предметов, соединенных чем-н. Теория множеств. Словарь Ожегова. S.I….. … Словарь Ожегова
Понятие множества обычно рассматривается как один из исходных (аксиоматических) терминов, т.е. как несводимый к другим терминам и потому неопределимый. Тем не менее, можно дать описание множества, например, в формулировке Георга Кантора:
Об операциях с множествами без боли
Какие возможности дает представительство? множеств в виде структур данных? Теперь на них можно выполнять различные функции. Две наиболее важные функции, которые могут быть выполнены над множествамэто пересечение и объединение.
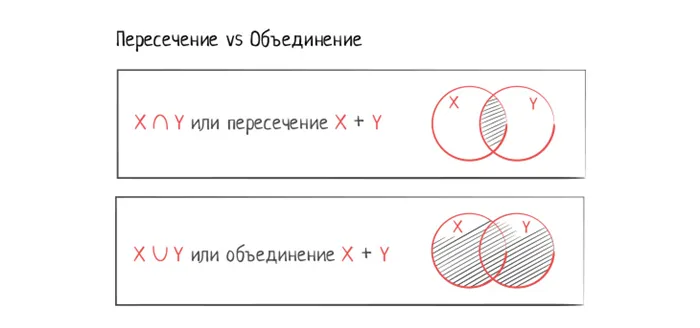
Пересечение множеств часто пишутся с такой Обозначение: X ∩ Y. Пересечение определяет, где два множества пересекаются. Другими словами, этот процесс возвращает все элементы, которые находятся в два множества. В нашем примере пересечение множества X и множества Y возвращает все книги, которые человек прочитал и которые у него есть дома. Хорошим ключом к пониманию этого пересечения является ключевое слово «и». Мы получаем книги, которые человек прочитал и которые у него есть дома. Хотя книги, созданные благодаря межсекторальности, находятся в двух множествах, мы не повторяем их, так как в множестве они могут быть только уникальными объектами.
Объединение двух множеств обозначается такX ∪ Y. Именно благодаря сочетанию у них есть что-то общее. множеств или объединённое множество. Другими словами, объединив множеств можно создавать новые множество предметы, которые присутствуют хотя бы в одном оригинале. множестве. В нашем случае профсоюз вернет все книги, которые человек прочитал, а также все книги, которые есть у человека дома. Если книга одновременно входит в набор X и набор Y, ее нельзя скопировать в новый набор Y. множестве после объединения, так как в множества Включены только уникальные предметы.
С помощью диаграммы Венна можно показать пересечение и объединение так:

Теперь давайте рассмотрим более сложные вещи. Слияние и пересечение — важные операции над множествамНо это лишь основы теории. Для решения более серьезных задач нам необходимо ознакомиться с другими функциями. Важно понимать разницу множеств и соответствующие дополнения множеств. Ниже мы рассмотрим, почему эти функции важны, но сначала нам нужно понять, как они работают.
Как следует из названия, разница множеств определяет разницу между множествами. Другими словами: Мы определяем, какие элементы сохраняются в множестве X, если мы удалим все элементы, которые находятся в в множестве Y. Это действие можно символизировать следующим образом такX — Y. В следующем примере разница между. множеством X и множеством Y — это элементы, которые присутствуют в множестве X, но не присутствуют в множестве Y. Они обозначаются буквами C, Z и W.

Относительное сложение — противоположность различию множеств. Например, относительное дополнение Y по сравнению с X дает все элементы из множества Y, которые не входят в множество X. Относительное дополнение можно сформулировать следующим образом так: X \ Y. Относительное дополнение X \ Y на самом деле дает такой один и тот же набор элементов с разностью Y — X. В данном примере множество Y меньше множества X. Единственный элемент, который находится в множестве Y, но не находится в множестве X, — это число 2.
По сути, мы просто вычитаем множество X из множества Y и ответить на вопрос: что есть в Y, чего нет в X?
Возможно, вы заметили, что в некоторых примерах мы имеем дело со строками, а в другой части элементами являются буквы и цифры. Здесь необходимо подчеркнуть один важный момент: множество Он может содержать любой элемент или объект. Вы можете думать о них множества как хэши: они включают любой вид сущности, когда сталкиваются с ней. во множестве только один раз.
Множества вокруг нас
Возможно, вы задавались вопросом, зачем вам нужно изучать теорию множеств. Это хороший вопрос, и пришло время на него ответить.
Вы догадались? Декорации повсюду. Это структуры данных, которые мы можем использовать при работе с различными языками программирования, такими как Python, Java, Ruby и JavaScript. и так Форварды. Если вы знакомы с этим или другими языками программирования, вы уже помните методы, с которыми можно работать с множествами.
Вот пример на JavaScript.
Конечно, названия методов могут отличаться в зависимости от языка. Например, метод has из примера Ruby выше называется include;, но эти методы работают одинаково. И в Python. с множествами вы можете использовать методы intersection, union и symmetric_difference.
Но в чем именно заключаются преимущества? множеств? Понятно, что с ними можно работать на разных языках программирования, но насколько велика польза на практике?

Один из моментов — множества Они могут сэкономить вам много времени. Помните все эти сложные операции — пересечение, объединение, разность? Вы уже догадались? Время, необходимое для выполнения этих операций, зависит от размера множеств. Это связано с тем, что для выполнения операций мы должны использовать все элементы. множества. Обычно даже огромные множества можно обойти относительно быстро.
Но как насчет основных функций? Как насчет добавления элементов в из множеств, Удаление элементов, поиск определенного элемента. в множестве? Все эти операции выполняются в постоянном времени или 0(1). Это очень мощный инструмент, что означает, что он что множества может быть даже более практичной структурой данных, чем словарь или хэш.
Но подождите, ведь все функции с множествами выполняются так быстро? Как это возможно? Как выяснилось, под капотом. множества являются хэшами. Теперь вся информация собрана. Большинство программистов знакомы с хэш-таблицами, но почему так это удобно для реализации. множества?
Это объясняется рядом факторов. Во-первых, в хэш-таблицах каждый элемент всегда имеет уникальный индекс. Это очень хорошо с точки зрения реализации. множеств, так как множества Он может содержать только уникальные элементы. Второй фактор: в хэш-таблицах порядок элементов не имеет значения. В множествах Порядок расположения элементов также не имеет значения. Наконец, хэш-таблицы обеспечивают фиксированное время доступа, равное 0(1). Это идеальный вариант для выполнения основных операций с множествами.
Заключение
Теория множеств используется в различных областях информатики. Это важная концепция для программистов, понимание которой помогает им эффективно работать с данными.
Адаптированный перевод книги «Теория множеств: метод к безумию баз данных» Вайдехи Джоши.
Никогда не останавливайтесь: В программировании говорят, что нужно продолжать учиться, даже если ты остаешься на полу. Развивайтесь вместе с нами — на Hexslet есть сотни курсов по разработке на разных языках и технологиях.
Союзное множество, пересекающееся множество, относительное дополнение, симметричная разность, истинное подмножество, абсолютное подмножество и так далее. множество (собственное подмножество, универсальное дополнение.
Отображение множеств
Отображение множества во множество — множество пересечений — это правило, согласно которому каждый элемент является множества с элементом (или элементами) множества. В сочетании с отдельный элемента, это правило называется однозначно определенной функцией или просто функцией.
Функция, как многие знают, обычно обозначается буквой — она присваивает уникальное значение каждому элементу, что приводит к. множеству .
А теперь я снова буду злиться. множество Теперь я снова буду раздражать учеников из ряда 1 и предложу им 6 тем для эссе (множество ):
Согласно (намеренно или ненамеренно =)) установленному правилу, каждый студент должен множества только одну тему для эссе. множества .
…и вы, наверное, не могли себе представить, что будете играть роль функционального аргумента =) =)
Элементы множества это область определения функции (обозначается ) и элементы множества — это диапазоны значений функции (обозначаются ).
Построенное отображение множеств обладает очень важным свойством: она является биекцией. В данном примере это означает, что каждый студент сопоставлен с Каждому студенту выдается уникальный Тема эссе и наоборот. Каждый Тема эссе назначается только одному студенту.
Однако не следует считать, что каждая иллюстрация двусторонняя. Если в строке 1 (к множеству ) добавить седьмого ученика, то парность один к одному теряется — либо ученик остается без темы (без парности вообще), либо тема назначается двум ученикам одновременно. В противоположной ситуации: если к множеству вы добавляете седьмой предмет, то назначение «один к одному» также теряется — один из предметов остается не назначенным.
Уважаемые студенты 1-го ряда, не расстраивайтесь, потому что остальные 20 студентов пойдут в университет, чтобы очистить пол от осенних листьев. Смотритель раздаст двадцать веников, и тогда произойдет встреча основной группы с вениками один на один…, а Вольдемар еще и в магазин успеет сбегать =).
Теперь рассмотрим функцию «школа» переменной. Просмотрите страницу «Функции и графики» (которая откроется в следующей вкладке) и найдите график линейной функции в примере 1.
Задумаемся, что это такое? Это правило каждый элемент диапазон определения (в данном случае все значения «x») соответствует отдельный ценность. С теоретической точки зрениямножественС теоретической точки зрения, существует отображение множества действительных чисел во множество действительных чисел:
Первое множество назовем на простом языке «ics» (независимая переменная или аргумент) и второй «igeks» (зависимая переменная или функция).
Далее рассмотрим известную притчу. Здесь правило помещает каждое значение «x» в свой квадрат, и происходит присваивание:
Итак, что же такое Функция одной переменной? Функция одной переменной — это правило, которое каждый значение независимой переменной из диапазона определения соответствует одно и только одно значение .
Как уже упоминалось в примере студента, не каждая функция является одноцелевой. Например, в случае функции, каждому «x» определения соответствует уникальный уникальный«Y» и наоборот — с каждым значением «Y» мы можем однозначно получить «X». Поэтому она является двусторонней функцией.
Мощность множества
Интуиция подсказывает, что этот термин относится к степени множества, т.е. количество его элементов. И интуиция нас не обманывает!
Мощность пустого множества равна нулю.
Мощность множества равна шести.
Мощность множества Количество букв в русском алфавите — тридцать три.
А в общем случае — сила любого конечного множества равно количеству элементов данного множества.
…возможно, не все до конца понимают, что такое конечное множество — если начать считать элементы этой таблицы. множества, то рано или поздно подсчет закончится. Что называется, и у китайцев в конце концов закончится.
Само собой, множества Их можно сравнивать по производительности, и их равенство в этом смысле называется эквивалентностью. Эквивалентность производительности определяется следующим образом:
Два множества ‘эквивалентны, если между ними можно установить четкую эквивалентность.
Множество учеников равно множеству тем рефератов, множество букв русского алфавита эквивалентен каждому множеству 33 элемента и т.д. Обратите внимание, что в каждом множеству 33 элемента — в этом случае значимо только их количество. Буквы русского алфавита нельзя сложить только в столько букв, сколько букв русского алфавита. с множеством Номера 1, 2, 3, …, 32, 33, но обычно со стадом из 33 коров.
Гораздо более интересным является случай с бесконечностью множествами. Бесконечности также имеют множество форм! . зеленый и красный. «Меньшие» бесконечности. множества – это счётные множества. Проще говоря, элементы такого множества могут быть пронумерованы. Примером ссылки является это множество Да — она бесконечна, но каждый элемент в принципе имеет номер.
Примеров тому множество. В частности, счетное множество всех четных натуральных чисел. Как вы можете это доказать? Вы должны установить переписку один на один. с множеством положительных целых чисел или просто нумерацией элементов: таким образом, устанавливается взаимно-однозначное соответствие, множества равномощны и множество исчисляемый. Удивительно, но по мощности четных натуральных чисел столько же, сколько и натуральных!
![]()
Множество целых чисел также является счетным. Его элементы могут быть пронумерованы, например, так:
Более того, счётно и множество Поскольку числитель — целое число (и, как только что было показано, может быть пронумерован), а знаменатель — натуральное число, рано или поздно мы столкнемся с каждой рациональной дробью и присвоим ей номер.
А вот множество Элементы логической дроби уже являются ненумерованными, т.е. их элементы не могут быть пронумерованы. Хотя этот факт очевиден, он не принимается во внимание в теории множеств. Мощность множества вещественных чисел также называется непрерывным, и по сравнению со счетным множествами является «бесконечным множество.
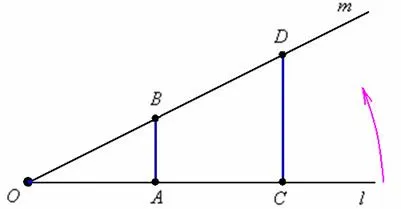
Поскольку между множеством и числовой прямой, существует соответствие один-к-одному (см. выше), то множество точки на арифметической прямой также не измеримы. Кроме того, на километровой и миллиметровой линии так много точек! Классический пример: вращая луч против часовой стрелки до совмещения с лучом, устанавливается соответствие один-к-одному между точками отрезков синей линии. Таким образом, точек на отрезке столько же, сколько и отрезков, и !
А вот множество Элементы логической дроби уже являются ненумерованными, т.е. их элементы не могут быть пронумерованы. Хотя этот факт очевиден, он не принимается во внимание в теории множеств. Мощность множества вещественных чисел также называется непрерывным, и по сравнению со счетным множествами является «бесконечным множество.
Множество рациональных чисел
Логические числа — это те же дроби, которые мы изучали до сих пор.
Рациональное число — это число, которое можно выразить в виде дроби, где a — числитель, а b — знаменатель.
Числителем и знаменателем может быть любое число, включая целые числа (кроме нуля, потому что на ноль делить нельзя).
Например, предположим, что a заменяется на 10, а b — на 2.

10, деленное на 2, равно 5. Мы видим, что число 5 можно представить в виде дроби, и поэтому число 5 содержит во множество рациональных чисел.
Легко видеть, что число 5 также относится и ко множеству является целым числом. Поэтому множество целых чисел входит во множество рациональные числа. И вот, во множество Рациональные числа — это не только дроби, но и целые числа, такие как -2, -1, 0, 1, 2.
Теперь представьте, что a заменено на 12, а b — на 5.

12 разделить на 5 равно 2,4. Мы видим, что десятичное число 2,4 может быть представлено в виде дроби, так что оно может быть преобразовано в во множество рациональные числа. Поэтому мы пришли к выводу, что во множество Рациональные числа включают не только дроби и целые числа, но и десятичные дроби.
Мы вычисляем дробь и получаем ответ 2.4. Но мы могли бы выделить целую часть в этой дроби:
Если мы выделим целую часть дроби, то получим смешанное число. Мы видим, что смешанное число также можно представить в виде дроби. Так что во множество рациональных чисел включает смешанные числа.
Из этого мы делаем вывод, что множество логические числа содержатся сами в себе:
- целые числа
- обыкновенные дроби
- десятичные дроби
- смешанные числа
Множество рациональных чисел обозначается латинской заглавной буквой Q.
Предположим, например, что дробь к множеству Рациональные числа. Мы пишем саму дробь, а затем используем обозначение ∈ Q, чтобы написать, что дробь принадлежит множеству рациональных чисел:
∈ Q
Предположим, что десятичное число 4,5 принадлежит множеству рациональных чисел:
Мы говорим, что смешанное число принадлежит множеству рациональных чисел:
∈ Q
Вводный урок по множествам завершена. В будущем мы рассмотрим множества может быть гораздо лучше, но на данный момент достаточно того, что мы рассмотрели в этом уроке.
Понравились ли вам занятия? Присоединяйтесь к нашей новой команде Vkonтакте и получать уведомления о новых курсах
Хотели бы вы поддержать проект? Воспользуйтесь кнопкой ниже.
15 thoughts on “Что такое множество?”
В первой части второго примера вы написали, что 5 не является делителем D, но в пояснении вы написали «2 не является множеству делитель числа 6″. Исправьте ошибку.
Да, там была опечатка. Мы исправим это.
Все понятно и изложено простым языком.
Я ничего не понимаю, все сложно и непонятно.
Все очень ясно и понятно.
Конечно, я не понимаю этого, после начала года с головной болью.
Спасибо! Все очень четко!
Большое спасибо, очень информативно.
Содержит ли множество всех множеств само себя?
Здравствуйте, большое спасибо за сайт!!!!
Верхняя страница) Я прогуливал математику в школе и теперь интересуюсь этим предметом).
Спасибо большое, я сейчас готовлюсь к ЕНТ, очень, очень помогли!
Привет, я могу быть, не так понял, но почему во множество Разве рациональные числа не включают в себя натуральные числа?
Т.к в множество целых чисел входит множество Если у вас нет натуральных чисел, то натуральные числа включены. в множество рациональные числа. В списке нет множества натуральных чисел, поскольку оно уже включено в целые числа. Надеюсь, я хорошо объяснил 😀
Добавить комментарий Отменить ответ
© 2015-2022 Математика с нуля. Пошаговое исследование математики Для начинающих. Категорически запрещается копировать материалы и размещать их на других ресурсах.
Числа вида a + bi ( a, b ∈ R ), где i =√-1 — мнимый единичный корень из минус единицы, являются множество комплексные числа C .
Часть вторая. Краткий обзор операций, обозначений и диаграмм Венна.
Как отмечалось в предыдущем разделе, одно из фундаментальных преимуществ теории заключается в том, что она множеств возникает не из какой-то конкретной теории, а из языка, который ее порождает. По этой причине основная часть данного раздела будет посвящена обозначениям, операциям и визуальному представлению теории. множеств. Давайте начнем с объяснения основных символов множества — элементы, которые ему соответствуют. В следующей таблице приведен пример множества A с тремя элементами:

A — это множество ‘1’, ‘2’ и ‘3’ элементы.
«1» — элемент множества A
Первая строка показывает множество A с тремя отдельными элементами (A = ), вторая строка показывает правильное представление одного конкретного элемента 1, соответствующего множеству A. Пока это достаточно просто, но теория множеств становится гораздо интереснее, когда мы добавляем второй множество — начинает путешествие по стандартным процессам.
Для приведенной выше таблицы нам необходимо добавить два дополнительных множества B и C со следующими элементами. три множества (A, B и C), в следующих примерах операции выполняются только на двух множествами, поэтому обратите пристальное внимание на то, какие множества перечислены в левой колонке. В таблице ниже перечислены пять наиболее распространенных операторов. множеств:

Функции: Перекресток — множество Элементы, которые приводят к множеству A и множеству B;
объединение (union) — множество Элементы, которые приводят к множеству A или множеству B;
подмножество (подмножество) — C является подмножеством измножеством A, множество C включено во множество A;
собственное (реальное) подмножествомножество — C является подмножеством A, но C не равно A,
относительное дополнение — множество элементов, принадлежащих A и не принадлежащих B.
Вот они, самые распространенные операции в теории. множествОни также очень популярны в других областях, помимо чистого сельского хозяйства. математики. Скорее всего, вы сталкивались с подобными операциями в прошлом, хотя и не обязательно в с такой терминологии, и я действительно использовал их. Хороший пример: попросите студента описать диаграмму Венна с двумя пересекающимися группами, и он интуитивно придет к правильному результату.
Посмотрите еще раз на последнюю строку, на соответствующее дополнение — какое необычное сочетание слов, не правда ли? По сравнению с чем? Если относительное дополнение A — B определяется как A, а не B, как мы можем сказать, что что-то не является B?
Универсальное множество — пустое множество
Оказывается, если мы хотим получить осмысленный ответ, мы должны сначала дать общую совокупность нашей проблемы множеств контекст. Часто это явно указывается в начале задания, когда принимаемые данные являются множества ограничиваются определенным классом объектов, для которых существует универсальный множество , являющееся общим множеством, который содержит все элементы для выполнения поставленной задачи. Например, если бы мы хотели работать со множествами только буквы английского алфавита, то глобальная множество U состоит из 26 букв алфавита.
Часть 3. Мощность и показательные множества
В предыдущих двух частях мы рассмотрели основы теории. множеств. В третьей части мы углубим наше понимание, рассмотрев наиболее важные свойства каждого из них. множестваОбщее количество уникальных элементов, которые он содержит.
Количество уникальных элементов во множестве, также известная как мощность, дает нам базовый ориентир для дальнейшего, более глубокого анализа. множества. Во-первых, мощность — это первое из уникальных свойств, которые мы исследуем, что дает нам возможность объективного сравнения различных видов с множеств, проверяя, существует ли биекция (это, с некоторыми оговорками, просто уточненный термин для функции ) от a множества от другого. Другой способ применения силы, а также которая является предметом данной части работы, позволяет нам оценить все возможные подгруппымножества, которые присутствуют в данном множестве. Это можно буквально применить к повседневным задачам принятия решений, будь то планирование бюджета на покупки в супермаркете или оптимизация портфеля акций.

Примеры мощности множеств
Например, в таблице выше показаны пять отдельных множеств с указанной мощностью в правой части. Как упоминалось ранее, символ мощности выглядит как символ абсолютного значения — значения, заключенного между двумя вертикальными линиями. Все примеры понятны, за исключением, пожалуй, последней строки, которая дает понять, что только отдельные элементы влияют на мощность множества.
Помните подмножества из предыдущей части статьи? Оказывается, что обоснованность определенных множества A и количество возможных подмножеств множества Удивительные отношения. Далее будет показано, что число под.множеств, могут быть получены из некоторых подгруппмножества, увеличивается с ростом производительности на предсказуемую величину:
Давайте подробнее рассмотрим следующий пример. Однако давайте сначала посмотрим на формулу. Давайте рассмотрим мощность как общее количество «позиций», которые представляют собой множество. При создании некоторых подмножества Для каждой возможной позиции принимается булево решение (да/нет). Это означает, что каждый добавленный элемент. к множеству (т.е. увеличение мощности на единицу) увеличивает число возможных субмножеств с множителем два. Если вы программист или ученый, вы сможете понять эту логику немного лучше, если будете знать, что все подмножества множества можно рассчитать с помощью таблицы двоичных чисел.
Показательное множество (булеан)
Прежде чем мы рассчитаем все подмножества для примера множества C, я хочу ввести последнее понятие — булево значение.
Булево значение обозначается заглавной буквой S, за которой следует начальная буква множество S (С). Булеан — это множество всех подмножеств C, включая пустое множество и само множество C. В следующей таблице показано булево число S(C) со всеми перестановками возможных подслоевмножеств для множества C, содержащийся в капитале множестве.
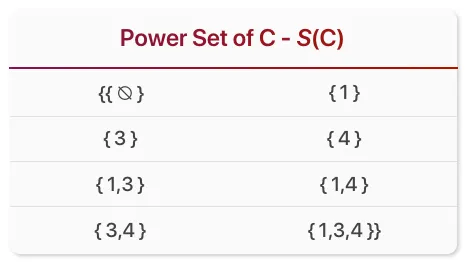
Для облегчения форматирования я расставил запятые между словами множествами***
Часть 4. Функции.
В этой части мы более подробно объясним функции теории множеств. Как и в случае с предыдущими понятиями, терминология стандартных функций в теории такова множеств незначительно отличается от других областей математики, и поэтому требует некоторого объяснения. Существует довольно много технических терминов, так Так что давайте сразу перейдем к делу! В первой таблице ниже приведены понятия области определения, области значения и значения функции:

Функция в мире теории множеств — В теории функций функция — это просто соответствие некоторых (или всех) элементов множества A некоторым (или всем) элементам множества B. В теории теории функций функция является функцией функции. В приведенном выше примере множество всех возможных элементов A называется областью определения; элементы A, которые используются в качестве входных значений в частности, называются аргументами. В правой части — множество всех возможных выходных значений (в других областях как математики «диапазон значений»), называется коконфигурацией; набор фактических выходных элементов B, соответствующих A, называется образом.
Пока ничего особенно сложного, просто новый способ указания параметров функций. Далее мы расскажем, как описать поведение этих функций соответствия с помощью стандартных типов функций.
Инъекции, сюръекции и биекции
В теории множеств Как сортировать корреспонденцию множеств К сожалению, у этих терминов много разных названий, что вносит дополнительную путаницу, поэтому мы сначала рассмотрим каждое определение, а затем обратимся к наглядным примерам. Все три термина описывают, как аргументы отображаются на изображения:
- Функция является инъективной ( или «один к одному» ), если каждый элемент в кообласти отображается не более чем на один элемент в области определения.
- Функция является сюръективной, если каждый элемент в кообласти отображается не менее чем на один элемент в области определения. (то есть образ и кообласть функции эквивалентны.)
- Функция является биективной, если каждый элемент кообласти отображается ровно на один элемент области определения.
Прочитайте еще раз список элементов, приведенный выше. Биекция — это просто функция, которая удовлетворяет двум предыдущим требованиям, т.е. функция инъективна и смежна. Инъективная функция не обязана быть конъюнктивной, а конъюнктивная функция не обязана быть конъюнктивной. Ниже приведен наглядный пример, где эти три классификации приводят к функции множеств, определяются четырьмя возможными комбинациями свойств инжекции и поверхности:
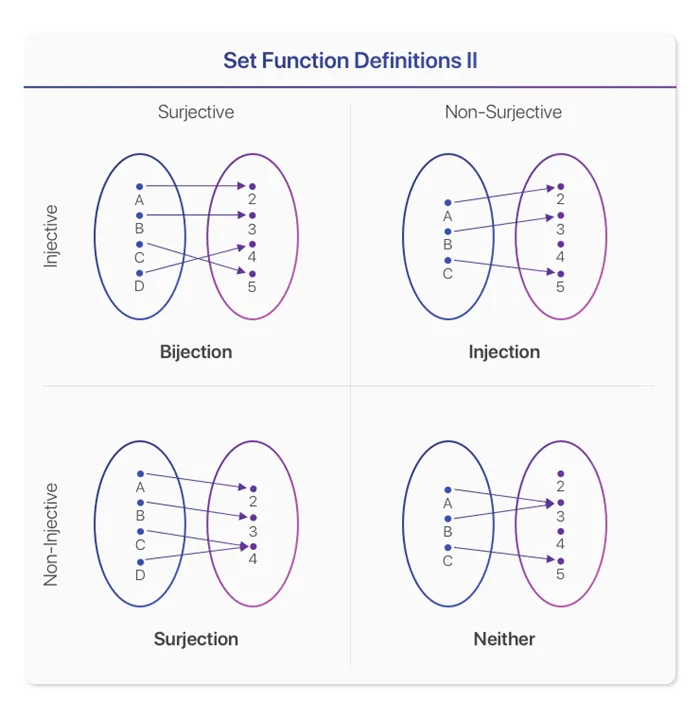
Инъекция (инъекция + инъекция), инъекция (инъекция + без инъекции), инъекция (без инъекции + инъекция), без классификации (без инъекции + без инъекции).
Вот и все! Теперь у нас есть рудиментарное понимание наиболее распространенных аналогий, с которыми мы сталкиваемся в мире. множеств. Однако это ни в коем случае не конец нашего пути, а, наоборот, начало.
Основные принципы теории множеств — Ключ к пониманию полей более высокого уровня математики. Чтобы продолжить наше восхождение на эти различные уровни, мы должны затем использовать наши знания теории множеств, чтобы понять одну из самых революционных теорий в истории. математикисистема аксиом Цермело-Френкеля.








