Другими словами, линия делит фигуру на две равные части. Точки частей фигуры, лежащие на прямой, перпендикулярной этой прямой, равноудалены от нее. Эта линия называется осью симметрии. Такой тип симметрии (относительно прямой линии) называется осевой симметрией.
Ось симметрии — что это такое? Фигуры, имеющие ось симметрии
Что такое ось симметрии? Это набор точек, образующих линию, на которой основана симметрия. Это означает, что если от линии отложить определенное расстояние в одну сторону, то оно отразится в другую сторону с тем же размером. Осью может быть что угодно — точка, линия или плоскость. Однако лучше поговорить об этом на реальном примере.
Чтобы понять, что такое ось симметрии, необходимо разобраться в самом определении симметрии. Это соответствие между определенной частью тела и произвольной осью, структура которой остается неизменной, а свойства и форма объекта остаются неизменными при его трансформации. Можно сказать, что симметрия является свойством отображаемого тела. Если фрагмент не может иметь аналогичного соответствия, это называется асимметрией или нерегулярностью.
Некоторые формы не обладают симметрией и поэтому называются неправильными или асимметричными. К ним относятся различные таблицы (кроме равнобедренных треугольников) и треугольники (кроме равнобедренных и равносторонних треугольников).

Виды симметрии
Чтобы полностью изучить эту концепцию, мы также обсудим несколько типов симметрии. Их можно разделить следующим образом:.
Само понятие симметрии часто является отправной точкой для теорий и гипотез древних ученых, которые были убеждены в математической гармонии Вселенной и проявлении божественного принципа. Древние греки свято верили, что Вселенная симметрична, потому что симметрия прекрасна. Человек давно использовал идею симметрии в своем познании образа Вселенной.
В пятом веке до нашей эры Пифагор считал, что сфера — самая совершенная форма, и что Земля имеет форму шара и движется таким же образом. Он также считал, что Земля движется в форме «центрального огня», вокруг которого должны вращаться шесть планет (как их тогда называли), Луна, Солнце и все остальные звезды.
А философ Платон рассматривал многогранник как воплощение четырех природных стихий.
- тетраэдр — огонь, так как его вершина направлена вверх;
- куб — земля, так как это самое устойчивое тело;
- октаэдр — воздух, нет каких-либо объяснений;
- икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Благодаря всем этим теориям правильный многогранник называется правильным многогранником.
Симметрия использовалась уже древнегреческими архитекторами. Все здания были симметричными, как видно из изображения храма Зевса в Олимпии.

Голландский художник М.К. Эшер также обращался к симметрии в своих картинах. В частности, мозаика с изображением двух птиц, летящих навстречу друг другу, легла в основу картины «День и ночь».
Наши искусствоведы не обошли вниманием правила симметрии, что видно на примере картины Васнецова «Богатыри».
Симметрия была важным понятием во всех видах искусства на протяжении веков, но в 20 веке ее важность признала и точная наука. Физические и космологические теории, такие как теория относительности, теория струн и абсолютно вся квантовая механика, являются точным доказательством. Со времен древнего Вавилона до передовых открытий современной науки мы можем проследить, как изучалась симметрия и открывались ее фундаментальные законы.
Симметрия геометрических фигур и тел
Внимательнее смотрите на геометрические тела. Например, ось симметрии параболы — это линия, которая рассекает это тело пополам через его вершину. Эта форма имеет только одну ось.
Это не относится к геометрическим фигурам. Оси прямоугольной симметрии также прямые, но их больше. Вы можете рисовать валы параллельно участку ширины и параллельно участку длины. Однако все не так просто. Здесь прямая линия не имеет симметричного стержня. Это связано с тем, что его концы неопределенны. Может существовать только центральная симметрия, но не симметрия.
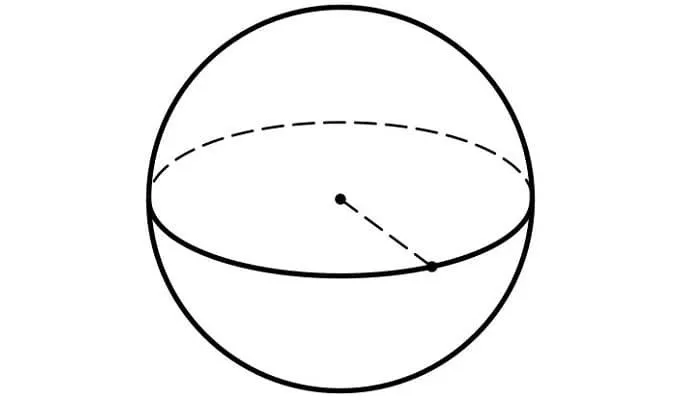
Следует также отметить, что некоторые тела имеют много симметрий. Вывести это несложно. Нет необходимости даже говорить, сколько осей симметрии имеет круг. Все линии, проходящие через центр окружности, симметричны, и эти линии бесконечны.
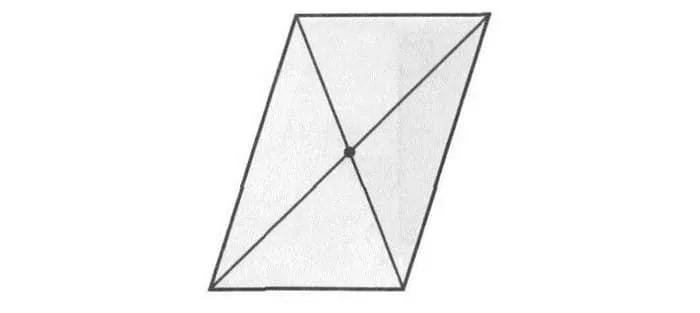
Некоторые четырехугольники могут иметь две оси симметрии. Однако второй должен быть перпендикулярен. Это относится к ромбам и прямоугольникам. В первом случае осью симметрии является диагональ, а во втором — центральная линия. Только квадраты имеют много осей.
В обычной жизни многие люди даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Эта концепция не является уникальной для математики.
Свойства осевой симметрии
- Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
- Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
- Обратное преобразование осевой симметрии есть та же осевая симметрия.
- Осевая симметрия – это поворот относительно оси симметрии на 180°.
Осевая симметрия — это движение. Это означает, что при преобразовании осесимметрии расстояние между точками сохраняется.
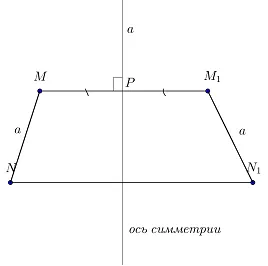
Если сечение MN симметрично относительно сечения M1n1 Для прямой a, mn = m1n1Чтобы доказать, что Mn = m
n1n1Докажите, что прямоугольные треугольники mnk и m
- P – это точка пересечения MM1 и прямой a;
- Q – это точка пересечения NN1 и прямой a;
- построим отрезок MK, перпендикулярный NN1;
- тогда точка K отразится в точку K1Чтобы доказать, что Mn = m
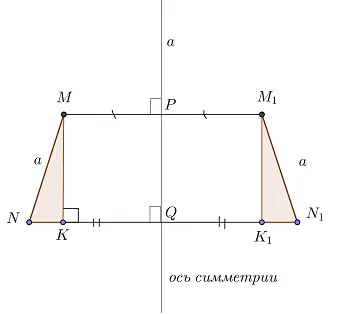
n1n1 Они равны. Стороны mn и m1n1n1mk = m
Фи.1 поскольку они перпендикулярны параллелям.1Точка n назначается на точку n
Итак.1Поэтому, поскольку треугольник равен на двух катетах, то и подчиненные равны, т.е. mn = m
n1n1Угол имеет осевую симметрию, а биссектриса является симметричным валом.
Фигуры, обладающие симметрией
Из любой точки на одной стороне угла проведите перпендикуляр к биссектрисе ядра и продлите его на другую сторону угла.
Поскольку KO = OM, точки k и m симметрично касаются биссектрисы угла.

- AO – общая сторона
- Из свойства биссектрисы: ∠ MAO = ∠KAO
- Треугольники KAO и MAO прямоугольные,
Следовательно, треугольник Изочелле также симметричен относительно биссектрис, вписанных в основание.
У равнобедренного треугольника есть три симметрии — биссектриса, медиана и высота каждого угла.
Прямоугольник имеет две оси симметрии. Каждый из них проходит через противоположное среднее значение.

Ромб имеет две оси симметрии. Это линии, содержащие диагонали.
Квадрат имеет четыре оси симметрии, так как является одновременно ромбом и прямоугольником.

В одном цикле существует бесконечное число симметрий — все они являются прямыми линиями, проходящими через центр круга.
Симметрия была частью жизни человека с древних времен. Украшения со знаками зеркальных отражений можно увидеть на древних зданиях древнегреческих кораблей. Аналоговые состояния были заимствованы наукой у природы.
Симметрия в повседневной жизни
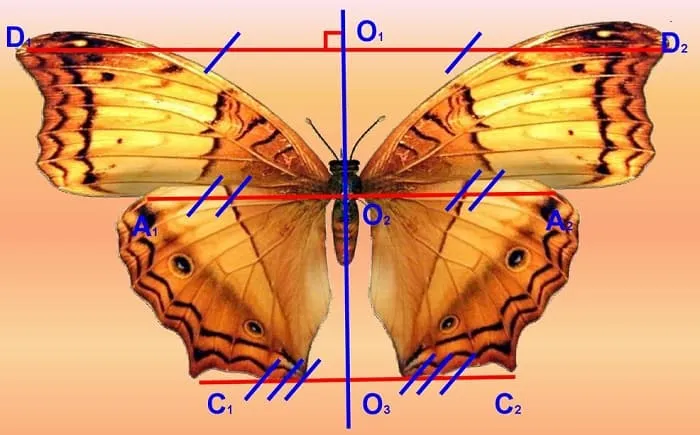
Зеркальные отражения часто встречаются в природе живых и неживых объектов. Снежные хлопья выполняют эту функцию. В растительном мире противоположные элементы растений уравновешены. Большинство листьев зеркально отражены по отношению к центральному стеблю. В животном царстве закон симметрии проявляется в наличии у животных правой и левой сторон. Представители большинства видов фауны имеют соединенные части тела, такие как уши, ноги, глаза, крылья и рога. Бабочки — яркие примеры зеркальной симметрии. Симметричный вал представляет собой прямую линию, проведенную вдоль центрального тела насекомого.
Он использует принцип симметрии в своем искусстве, потому что человек — часть природы. В искусстве свойство отражения используется для создания красоты и гармонии. В архитектуре пропорция имеет практическую функцию — она придает зданию устойчивость и надежность. В повседневных предметах единообразие можно обнаружить в расположении фрагментов узора ковра, принтов на ткани и рисунков на обоях.
Стремление к симметрии, вероятно, связано с земным притяжением. Люди интуитивно воспринимают симметрию как некую стабильность. Принцип отражения в зеркале играет важную роль в жизни человека. Стремление к гармонии и красоте побуждает человечество следовать правилам пропорций.
Что такое осевая симметрия? Само слово «симметрия» уходит корнями в греческий язык и описывает определенный набор существующих частей объекта и их пропорциональность.
Слово «симметрия» происходит от греческого слова symmetria, означающего пропорциональность. В нашем случае симметрия — это свойство геометрической фигуры, которое должно проявляться.
Понятие симметрии
Учитель: Симметрия давно используется в дизайне, орнаментах и архитектуре. Где еще можно использовать симметрию? Студент: строительство домов — строительство предметов быта. Учитель: Да, но симметрия используется не только там, где люди что-то строят! Каждый день мы видим симметричные объекты в природе. Назовите три таких предмета! Студент: бабочки, цветы, формы листьев! Морская звезда, снежинка, нарезанное яблоко.
Существует множество симметрий, которые выглядят странно и причудливо, но мы рассмотрим две симметрии на плоскости. Это касается точек и линий.
Обратите внимание, что две фигуры равны симметрично относительно линии (рис. 131). Каждая точка фигуры с осью симметрии, не принадлежащая этой оси, может быть разбита на пару точек симметрии (рис. 132).
Осевая симметрия
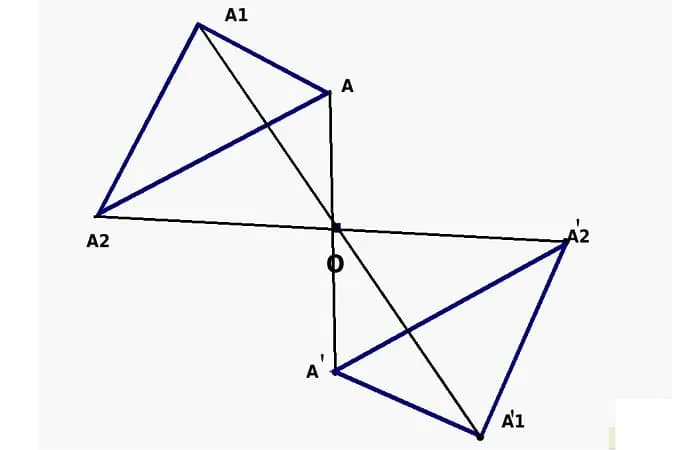
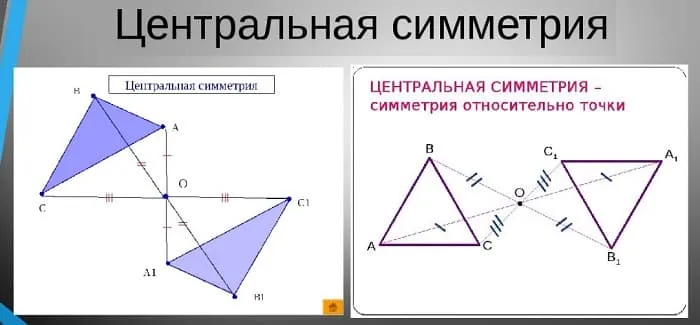
Симметрия вокруг точки называется центральной симметрией.

Центральная симметрия
Фигуры с центром симметрии — это понятие, которое учащимся дается труднее, чем фигуры с осью симметрии. Для облегчения распознавания и понимания рекомендуется показывать как можно больше примеров из естественной среды.
В зависимости от уровня математической подготовки учащихся в классе, можно обратить внимание на то, что прямая линия — это фигура с бесконечным количеством осей и центром симметрии.
С помощью классной работы материал может быть дополнен различными графическими форматами.
Вращательная симметрия, другое название осевой симметрии, используется в естественных науках. Это понятие относится к отражению объекта в зависимости от его вращения вокруг прямой линии.
Существует множество осевых объектов и геометрических фигур. Сначала в качестве примера необходимо рассмотреть прямоугольник и ромб с двумя такими осями.
Фигуры, имеющие несколько осей симметрии
Для прямоугольника характерны две оси симметрии. Это линии, проходящие через противоположные центральные точки.
Ромб одинаковый (две оси). Оси — это прямые линии, содержащие диагонали этой геометрической фигуры.
Интересен квадрат с четырьмя осями. Эта фигура является одновременно ромбом и прямоугольником. Другие типы прямоугольника вообще не имеют оси симметрии.
Рисунок 5: Оси симметрии ромба
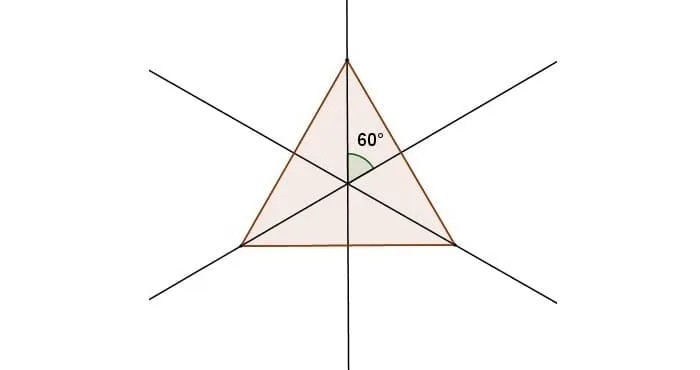
Единственная фигура с тремя осями симметрии — это равносторонний треугольник. Это только медиана, линия, соединяющая средние значения на его стороне. Медиана равностороннего треугольника является одновременно его биссектрисой и высотой.
На рисунке 6 показаны оси симметрии равностороннего треугольника
В обычной жизни многие люди даже не задумываются о том, как часто они встречают различные виды симметрии. Эта концепция характерна не только для математического мира.
В обычной жизни многие люди даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Эта концепция не является уникальной для математики.
Признание этого факта давно принято великими умами на протяжении веков. С древних времен до наших дней определение этого понятия прошло долгий путь.
Осознание того, что это событие прошло долгий путь во времени, изучалось большими умами на протяжении веков. С древних времен до наших дней определение этого понятия прошло долгий путь эволюции.
Осознание того, что это событие прошло долгий путь во времени, изучалось большими умами на протяжении веков. С древних времен до наших дней определение этого понятия прошло долгий путь эволюции.
Что такое ось симметрии
В более широком смысле симметрия означает сохранение чего-то неизменным при определенном преобразовании. Некоторые геометрические фигуры также обладают этим свойством.

В случае с геометрической фигурой симметрия означает, что если эту фигуру преобразовать, например, повернуть, то некоторые ее свойства останутся неизменными.
Геометрическая симметрия
Возможности таких преобразований варьируются от формы к форме. Например, круг может сколько угодно вращаться вокруг своей центральной точки и оставаться кругом. Ничего не меняется.
Концепция симметрии может быть проиллюстрирована без необходимости вращения. Достаточно спроектировать вертикальную прямую в любом месте фигуры, которая проходит прямо из центра окружности и соединяет две точки окружности. Пересечение с линией делит эту часть на две части, которые равны друг другу.
Другими словами, линия делит фигуру на две равные части. Точки части фигуры, перпендикулярной данной прямой, равны ей. Эта линия называется симметричным валом. Такой тип симметрии относительно прямой линии называется осевой симметрией.
Другими словами, линия делит фигуру на две равные части. Точки частей фигуры, лежащие на прямой, перпендикулярной этой прямой, равноудалены от нее. Эта линия называется осью симметрии. Такой тип симметрии (относительно прямой линии) называется осевой симметрией.
Количество осей симметрии
Осевая симметрия также наблюдается в природе. Он может наблюдаться в двух вариантах.
Первый тип — радиальная симметрия, которая предполагает наличие множества осей. Это характерно, например, для морских звезд. Для наиболее развитых организмов характерна билатеральная или двусторонняя симметрия с одной осью, делящей тело на две части.
В человеческом теле также существует двусторонняя симметрия, но она не идеальна. Ноги, руки, глаза и легкие симметричны, но не сердце, печень и селезенка. Существует даже внешнее отклонение от билатеральной симметрии. Например, очень редко у человека бывает одинаковый оливковый цвет на обеих щеках.
Центры симметрии представляют большой интерес для ученых. В геометрии существует множество таких объектов. К ним относятся прямые линии, отрезки, круги и прямоугольники. Центры симметрии также встречаются в природе.
В геометрии 8 класса существуют твердые симметрии, такие как центры, оси и зеркала. Чтобы не зацикливаться на всем этом, больше тренируйтесь. Рисуйте, наблюдайте, делайте выводы о симметрии и решайте больше задач. Есть несколько упражнений для тренировки. Мы верим в вас!
Задачи на самопроверку
Задача 1. Посмотрите на симметричные геометрические фигуры и назовите типы симметрии.
Вы рассмотрели примеры осевой и центральной симметрии и знаете, что
Симметрия относительно прямых линий является осевой, а симметрия относительно точек — центральной
Задача 2. m и n точек, l, ось l симметрии. Ориентация
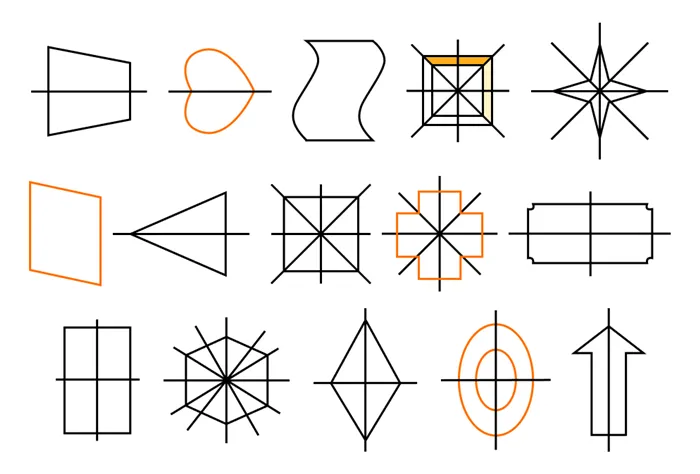
и п1 -симметричны относительно M и N в строке L. Докажите, что Mn = m1n1n1Подсказка: Объясните перпендикулярность n и n
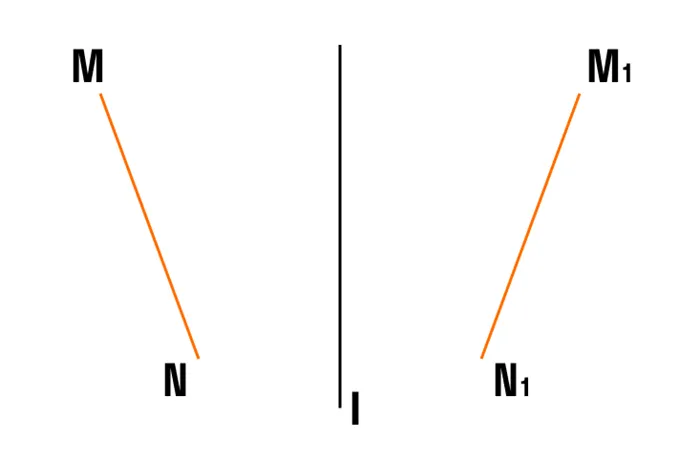
на линию ММ.1.1Чтобы доказать, что Mn = m
Осевая симметрия








