Однако в таком виде это решение имеет те же недостатки, что и многосеточный метод. А именно, наблюдается ярко выраженная и отчетливая «жесткость» низкочастотной составляющей функции гравитации. Проще продемонстрировать эту проблему наглядно.
Центр масс — формула и методы определения координат
Физическое понятие центра тяжести (ЦТ) было введено для решения задач, связанных с механическим движением (динамическим) или покоем (статическим) отдельных объектов (частиц) и систем объектов под действием внешних сил. Понятие МС эквивалентно понятию центра инерции. Центр тяжести (ЦТ) объекта не обязательно совпадает с его центром масс. Уравнение для нахождения координат МС использует значение массы и координаты отдельных точек системы.
Точка, через которую проходит направление действия всех сил, придающих телу ускоренное движение, называется центром тяжести. Когда тело, образно говоря, движется, это означает, что результирующие силы направлены через МС. Внедрение этой концепции в механические приложения облегчает расчеты с использованием системы координат, на которую ссылается МС. Если к системе тел не приложены внешние силы, то КМ движется с постоянной скоростью. Во многих проблемах форму и размеры тела можно игнорировать, изучая только поведение МС.
Формулы для вычисления координат ЦМ
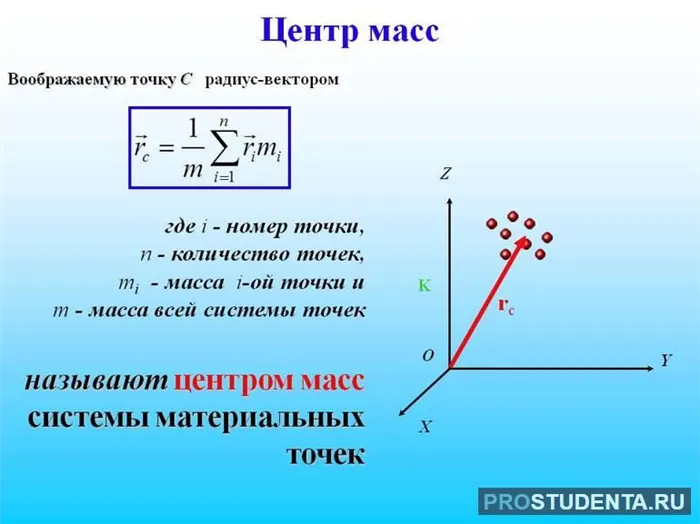
Если дана система, состоящая из N тел (частиц) с массой m i, расположенных на расстоянии ri (вектор радиусов в каждой точке) относительно центра координат, то для нахождения координат точки CM R c нужно сделать следующее. использовать следующие типы.
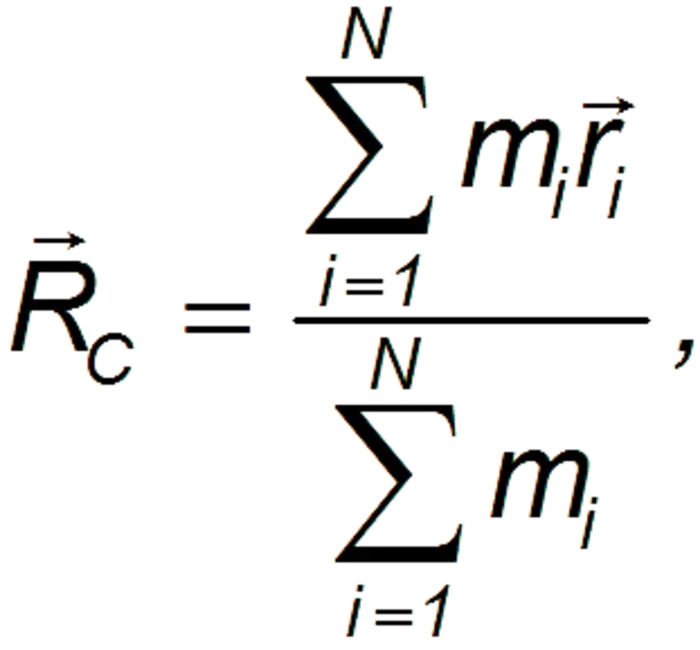
Для твердых тел с непрерывно распределенными массами общая формула для МС для определения их положения в пространстве имеет вид
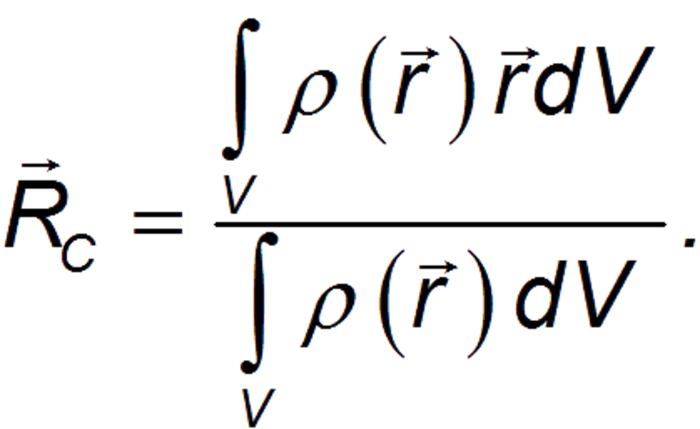
где ρ — плотность материала, из которого состоит объект. Уравнение (2) применимо к общему случаю, когда плотность изменяется в зависимости от координат точки.
Для физических объектов с равномерным распределением массы, т.е. плотность одинакова независимо от координат, местоположение МС может быть определено следующим уравнением
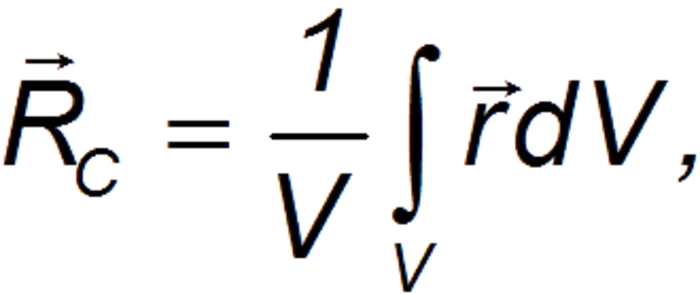
Центр тяжести
Согласно законам Ньютона, все объекты, находящиеся в свободном падении на поверхности Земли, будут двигаться, образно говоря, с ускорением g, если они не вращаются перед падением. Равновесие силы тяжести, которая является суммой сил, приложенных к отдельным частям тела, проходит через МС. Эта точка также является центром тяжести. МС — это более общее понятие, чем центр тяжести, и имеет смысл только для твердых тел, находящихся под действием силы тяжести в гравитационном поле. Для однородного поля (например, вблизи поверхности Земли) МС объекта совпадает с его МС.
Точное решение гравитационного взаимодействия системы N тел относится к алгоритму второго порядка сложности. На каждый объект действует гравитация всех других объектов в системе.1 Поэтому сила гравитационного взаимодействия должна быть рассчитана для каждой из N2/2 пар.
Определение понятия
Точка, через которую проходит направление действия всех сил, придающих телу ускоренное движение, называется центром тяжести. Когда тело, образно говоря, движется, это означает, что результирующие силы направлены через МС. Внедрение этой концепции в механические приложения облегчает расчеты с использованием системы координат, на которую ссылается МС. Если к системе тел не приложены внешние силы, то КМ движется с постоянной скоростью. Во многих проблемах форму и размеры тела можно игнорировать, изучая только поведение МС.
Если дана система, состоящая из N тел (частиц) с массой m i, расположенных на расстоянии ri (вектор радиусов в каждой точке) относительно центра координат, то для нахождения координат точки CM R c нужно сделать следующее. использовать следующие типы.
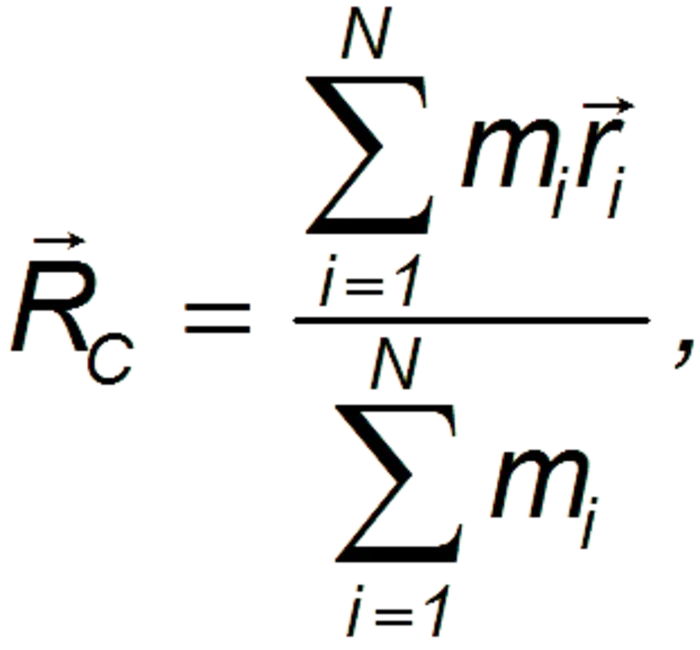
Для твердых тел с непрерывно распределенными массами общая формула для МС для определения их положения в пространстве имеет вид
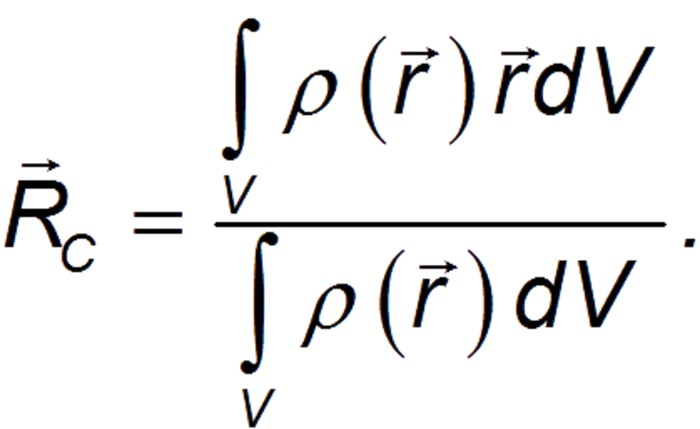
где ρ — плотность материала, из которого состоит объект. Уравнение (2) применимо к общему случаю, когда плотность изменяется в зависимости от координат точки.
Для физических объектов с равномерным распределением массы, т.е. плотность одинакова независимо от координат, местоположение МС может быть определено следующим уравнением
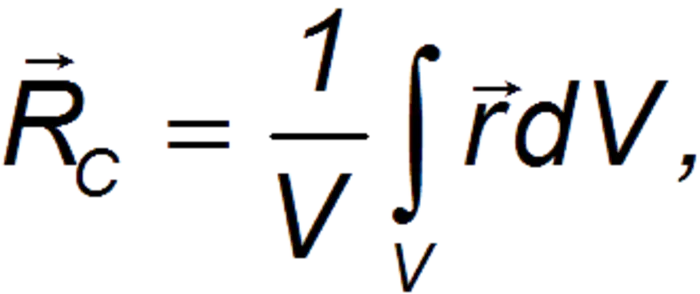
Центр тяжести
Согласно законам Ньютона, все объекты, находящиеся в свободном падении на поверхности Земли, будут двигаться, образно говоря, с ускорением g, если они не вращаются перед падением. Равновесие силы тяжести, которая является суммой сил, приложенных к отдельным частям тела, проходит через МС. Эта точка также является центром тяжести. МС — это более общее понятие, чем центр тяжести, и имеет смысл только для твердых тел, находящихся под действием силы тяжести в гравитационном поле. Для однородного поля (например, вблизи поверхности Земли) МС объекта совпадает с его МС.
Релятивистская физика
Если скорость частицы близка к скорости света (300 000 км/с), то для расчета необходимо использовать уравнение, выведенное Эйнштейном в Специальной теории относительности (СТО).
Понятие КМ также используется в релятивистской механике, но формула для вычисления положения R c выглядит так же, как в уравнении (1), но меняется, вместо массы частицы m i, энергия этой частицы Используется. Частица Ei. В этом случае вместо полной массы m — сумма энергий всех N частиц.
Точное решение гравитационного взаимодействия системы N тел относится к алгоритму второго порядка сложности. На каждый объект действует гравитация всех других объектов в системе.1 Поэтому сила гравитационного взаимодействия должна быть рассчитана для каждой из N2/2 пар.
Скорость центра масс
Уравнение для скорости центра тяжести ($).<\overline
где $ \overline$ — полный импульс системы частиц- $M$ — масса системы. Уравнение (8) применимо к движению со скоростью гораздо меньшей, чем скорость света.
Когда система частиц замкнута, суммарная тяга ее частей остается неизменной. Поэтому скорость центра тяжести постоянна. Считается, что центр тяжести замкнутой системы движется по инерции, т.е. линейно и равномерно, и это движение не зависит от движения компонентов системы. В закрытой системе действуют внутренние силы, и в результате их действия части системы могут ускоряться. Однако это не влияет на перемещение центра тяжести. Скорость центра тяжести не изменяется под действием внутренних сил.
Примеры задач на определение центра масс
Задание. Система состоит из материальных точек (рис. 2) и координат их центра тяжести.
Разрешение. Рассмотрим рис. 2. Центр тяжести системы находится в плоскости и поэтому имеет две координаты ($ x_c, y_c $). Найдите их с помощью следующего уравнения
Вычислите массу этой точечной системы.
В этом случае отклонение центра тяжести, $ x _\$, дается следующим образом
Ответ. $ x_c = 0,5 \ b $; $ y_c = 0,3 \ b $
Задание. Космонавт массой $M$ неподвижен относительно космического корабля массой $M$. Двигатели космического корабля выключены. Человек начинает тянуться к космическому кораблю с помощью легкой веревки. На какое расстояние космонавт ($s_1 $) и космический корабль ($s_2 $) долетят до точки встречи? Первоначально расстояние между ними составляет $s$.
Решение. Центры тяжести корабля и космонавта лежат на прямой, соединяющей эти объекты.
В космосе, где нет внешних сил, центр тяжести замкнутой системы (космический корабль-астронавт) остается неподвижным или движется с постоянной скоростью. В выбранной (инерциальной) системе координат он остается неподвижным. Даже так:.
Предположим, например, что область левого нижнего угла является координатной, а область правого верхнего угла — координатной. Сумма координат этой области —+ равна и координатам ее центра, так как общее число элементов равно 25.
Вычисление положения
Предположим, что тело — это ряд материальных точек на прямой линии с разными массами. Проблема заключается в том, чтобы найти его центр. Для этого мы принимаем систему координат по оси x, которая совпадает с линиями точек. Тело помещается на невесомую опору и находится под воздействием земного притяжения. Это условие позволяет воспользоваться тем, что центр тяжести совпадает с положением силы тяжести.

Каждая материальная точка имеет свою прочность, m1g, m2g… .mng, которая имеет свою собственную силу. Если тело оставить в покое, оно находится в свободном падении. Остановить тело — значит поддержать его, но так, чтобы оно было сбалансировано. Это означает, что сила реакции опоры должна проходить через центр тяжести, так как результирующее равновесие также проходит через центр тяжести.
Это означает, что силы реакции опоры согласованы с гравитационными силами, действующими на все тело, и что их крутящие моменты также проходят через тело. Используя координатные оси, точки x1, x2…. .xn и CMxc могут быть назначены позиции. Чтобы сбалансировать организм, необходимо соблюсти два условия.
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: f = (m1 + m2 + … + mn) * g. Если вращение выбрано против часовой стрелки, то все гравитационные моменты будут отрицательными по отношению к валу, а все опорные моменты — положительными. Тогда мы пишем F * xc = (m1 x 1 + m2 x 2 + … + mn xn) * g.
Из последнего уравнения координаты KM могут быть выражены как: xc = ((m1 x 1 + m2 x 2 + … + mn xn)* g) / F. В этом уравнении выражение для F можно заменить. В результате ускорение свободного падения уменьшается и становится: xc = (m1 x 1 + m2 x 2 + … + mn xn) / (m1 + m2 + … + mn). Этот человек выглядит утомительно, но его легко запомнить. Числитель — произведение масс материальных точек на координаты, а знаменатель — масса всего тела.
Если точки не лежат на прямой, то координаты центрального элемента остаются неизменными. Другими словами, приведенное выше уравнение применимо к любому положению тела относительно координаты y.
Таким образом, его можно применить к осмотру объектов в пространстве, поскольку все направления в существующем мире равноправны.
Геометрический способ определения
Для простейших симметричных форм КМ можно определить геометрическими методами. Для этого используются свойства диагонали и медианы. Предположим, что существует четырехугольник произвольной формы. Он изготовлен из однородного материала.
Идея расчета заключается в том, что фигуру нужно разделить на два треугольника. Для этого нарисуйте диагонали, которые разделят фигуру на два тела. Затем проведите три перпендикулярные линии на каждом треугольном теле. Их пересечение будет КМ. В результате вместо четырехугольников можно рассмотреть два важных момента.
Их массы различны, но МС располагается на соединяющей их части. Теперь четырехугольник можно разделить на два других треугольника и проделать с ними ту же операцию. Это занимает две секции, в которых одновременно размещается КМ. Поэтому их положение определяется их пересечениями.
Этот же подход можно использовать для более сложных форм, таких как шестиугольники и восьмиугольники. Тело сначала делится на прямоугольники, а затем на треугольники. Найдите КМ полученной фигуры и определите точки пересечения. Следует понимать, что МС может быть вне диапазона.
Однако в реальных ситуациях встречаются элементы неправильной формы. К ним невозможно применить расчетные или геометрические методы. Поэтому необходимо экспериментально исследовать, где находится ЦМ.
Например, предположим, что у вас сложное тело неправильной формы. Чтобы найти МС, необходимо разместить объект в пространстве. На него действуют две силы: сила тяжести и реакция вала. Первый вращает форму с определенной скоростью до тех пор, пока гравитационный момент на валу подвеса не станет нулевым. Это означает, что точка опоры, ось и центр тяжести находятся на одной вертикали.
Чтобы определить местоположение МС, необходимо использовать другую точку для подвешивания тела. На самой диаграмме обратите внимание, где проходит вертикальная линия.
Повторив этот эксперимент не менее трех раз, вы сможете определить точку пересечения осей, которая будет являться искомым ЦМ. И чем больше вы будете экспериментировать, тем точнее будет его определение.
Предположим, например, что область левого нижнего угла является координатной, а область правого верхнего угла — координатной. Сумма координат этой области —+ равна и координатам ее центра, так как общее число элементов равно 25.
Условия поступательного движения тела
Если все части тела движутся одинаково и поступательно, то для решения задачи тело заменяется материальной точкой и все вычисления производятся только для этой точки.
Рисунок 1.Материальная точка.
Возникает вопрос — где находится эта точка?
Чтобы ответить на этот вопрос, можно взять широкую линейку, прикрепить нитки к разным точкам на верхней поверхности линейки и потянуть ее в разные стороны.
Вы увидите, что линейка не всегда идет прямо. Часто он сначала вращается, а затем начинается образное движение.
Сравнивая случаи различных направлений тяги для одной и той же точки, можно убедиться, что существует только одно положение для движения линейки вперед. Еще один момент — положение правителя отличается, но также уникально.
Мы также видим, что точка, к которой приложена сила, может двигаться вдоль прямой, по которой направлен толчок. Это обеспечивает неизменность положения линейки и ее стабильное перемещение. Поэтому при транспортировке важно, чтобы сила тяги была направлена вдоль этой прямой линии.
Центр масс
Если вы проведете на линейке много таких линий, то обнаружите, что они пересекаются в одной точке. Таким образом, независимо от направления силы, на линейке (и других телах) существует точка, в которой приложение силы всегда вызывает образное движение.
Точка пересечения линий, к которым должна быть направлена сила, чтобы тело двигалось вперед, называется центром масс.
Это определение указывает на то, что когда тело движется определенным образом, вектор сил, вызывающих ускорение, проходит через центр масс. Тело ведет себя так, как будто вся его масса сосредоточена в этой точке. Поэтому в задаче можно рассматривать только эту единственную материальную точку, т.е. центр масс тела.
Центр масс иногда называют центром тяжести, поскольку под действием силы тело движется определенным образом. В приведенном выше эксперименте линейка не может перемещаться по столу, а лишь отмечает положение, в котором находится, что и происходит.
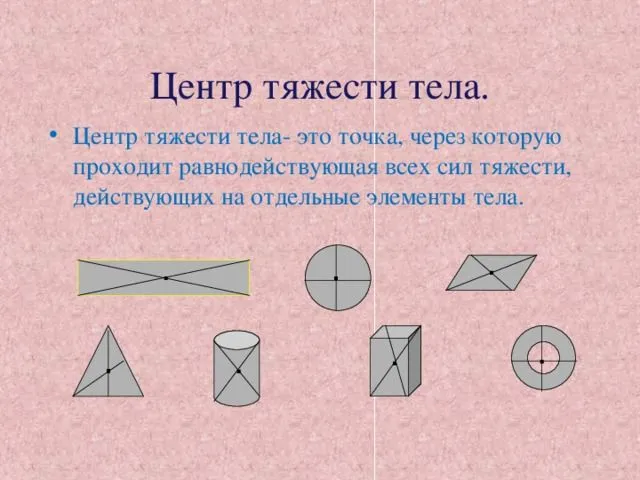
Рисунок 2. Центр тяжести тела.
Расположение центра масс
Из приведенного выше опыта с линейкой видно, как найти положение центра масс. В случае с симметричной линейкой он находится в центре симметрии. То же самое можно сказать об однородных симметричных телах и симметричных механических системах.
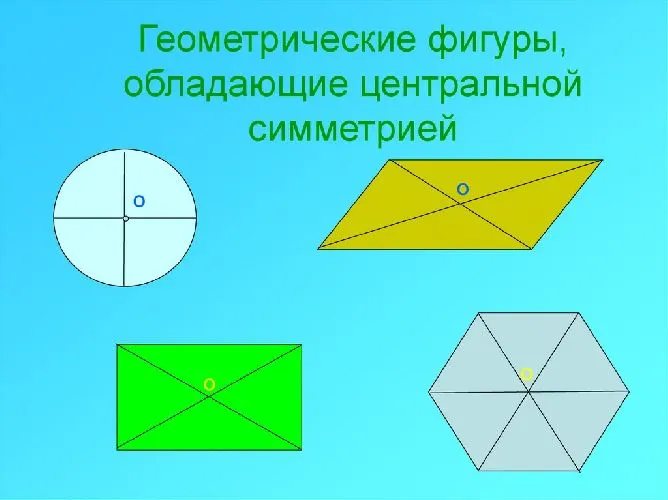
Рисунок 3.Рисунок 3: Форма симметрии центра.
Если тело асимметрично, найти центральный центр масс гораздо сложнее. Точный тип центра любого объединения преподается на курсах теоретической инженерии, используя метод тоталитарного учета. Приведенный выше опыт используется для нахождения приближения к этой точке.
Центр масс не обязательно является точкой самого тела. Например, в случае с кольцом он находится в центре симметрии, который не принадлежит самому кольцу.








