Структура личности человека представляет собой набор характеристик и атрибутов, которые условно делятся на положительные и отрицательные.
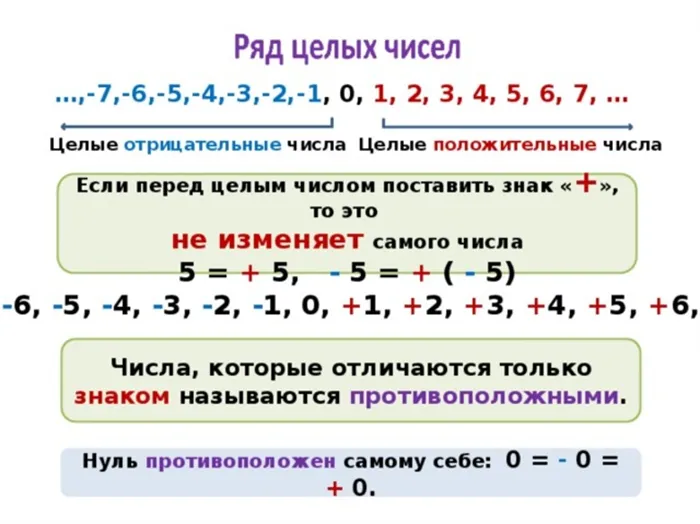
Целые числа
Целые числа — это расширения множества натуральных чисел 1, получающиеся в результате сложения нуля и отрицательных чисел 2. Необходимость рассмотрения целых чисел обусловлена тем, что одно натуральное число нельзя вычесть из другого. Только меньшие числа могут быть удалены большими числами.. Если вводятся нулевые и отрицательные числа, вычитание становится полной операцией, например, сложение 3.
Если дробное представление не содержит дробь (но может содержать знак), то действительное число является целым. Примеры действительных чисел:.
Число 142857? 0; -273 является целым числом. Число 5½? 9,75 не является целым числом.
Множество целых чисел называется Z> (от немецкого Zahlen «числа» 4). Раздел математики, называемый теорией чисел, посвящен изучению свойств целых чисел.
Содержание
Согласно своей структуре, множество целых чисел состоит из трех частей
-
(или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…) 5. — число, обозначаемое 0. Его определяющее свойство: 0 + n = n + 0 = n для любого числа n .
- Целые отрицательные числа.
Например, 4 | = 4; | -5 | = 5; | 0 | = 0.
Алгебраические свойства
На множестве целых чисел определены три основные арифметические операции. Это сложение, вычитание и умножение. Существует также важная операция деления на остаток, особенно для целых и натуральных чисел. Наконец, целые числа определяются для того, чтобы числа можно было сравнивать.
Сложение и вычитание
В следующей таблице приведены основные свойства сложения7 для целых чисел a, b и c.
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность ( переместительность ) | a + b = b + a |
| Ассоциативность ( сочетательность ) | a + ( b + c ) = ( a + b ) + c |
| Свойство нуля | a + 0 = a |
| Свойство противоположного элемента | a + ( − a ) = 0 |
При сложении и вычитании целых чисел соблюдаются следующие правила для знаков 7-8. Это необходимо учитывать при открытии скобок.
-(a) = a; -(a + b) = —a —b; -(a —b) = —a+b.
Правило 9 для сложения целых чисел.
- При сложении целых чисел с одинаковыми знаками надо сложить их абсолютные величины и приписать ей знак слагаемых. Пример; − 14 + ( − 28 ) = − 42 .
- При сложении целых чисел с разными знаками надо сравнить их абсолютные величины, из большей вычесть меньшую и приписать результату знак того слагаемого, у которого абсолютная величина больше. Примеры: − 4 + 9 = 9 − 4 = 5 ; − 9 + 4 = − ( 9 − 4 ) = − 5 .
- Вычитание a − b для целых чисел всегда выполнимо, и результат можно найти как a + ( − b ). Пример: 26 − 51 = 26 + ( − 51 ) = − 25 .
- Геометрически сложение можно наглядно представить как смещение числа вдоль числовой оси (см. рисунок в начале статьи), причём прибавление положительного числа вызывает смещение направо, а отрицательного — налево. Например, для числа − 3 прибавление к нему 4 означает смещение его вправо на 4 единицы; наглядно видно, что получается + 1. Аналогично − 3 + ( − 4 ), смещая − 3 влево на 4 единицы, получим в результате − 7 .
- Вычитание можно наглядно представить аналогично, но в этом случае, наоборот, вычитание положительного числа вызывает смещение влево, а отрицательного — вправо. Например, 5 − 7 смещает 5 на 7 единиц к числу − 2, а 5 − ( − 7 ) смещает его вправо к числу 12 .
Умножение и возведение в степень
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность ( переместительность ) | a × b = b × a |
| Ассоциативность ( сочетательность ) | a × ( b × c ) = ( a × b ) × c |
| Свойство единицы | a × 1 = a |
| Свойство нуля | a × 0 = 0 |
| Дистрибутивность (распределительность) умножения относительно сложения | a × ( b + c ) = a × b + a × c |
При умножении целых чисел следуйте правилам знаков 7-8. Это следует учитывать при открытии скобок.
(-a)b = a (-b) = —a b; (-a) (-b) = a b
Результат: произведение чисел с одинаковыми знаками положительно, с разными знаками — отрицательно.
Умножение целых чисел определяется так же, как и для натуральных чисел.
Свойство умножения для целых чисел также совпадает со свойством умножения для целых положительных чисел.
Упорядоченность
Целое число является положительным, если оно больше нуля, и отрицательным, если оно меньше нуля. Целые положительные числа — это натуральные и только натуральные числа. Отрицательное целое число противоположно положительному целому числу. Ноль не является ни положительным, ни отрицательным. Каждое отрицательное число меньше положительного числа 2.
Умножьте уравнение на 100, так как в периоде стоит двузначное число. Если период содержит одну цифру, умножьте уравнение на 10; для трех — умножьте на 1000. Чем больше цифр в периоде, тем больше нулей должно быть после 1 в числе, умноженном на уравнение.
Использование целых чисел при описании изменения величин
Изменение размера объекта или объектов лучше всего описывается с помощью целых чисел. Это символы «+» или «-«, которые четко указывают на увеличение или уменьшение значения или его изменение, если используется ноль. Это одно из основных различий между множествами целых чисел и множествами натуральных чисел.
Чтобы проиллюстрировать это, можно использовать пример, показывающий, как рассчитывается изменение цены.
На полках хранилось много книг. Затем было выдано десять новых экземпляров. Параметр 10 означает изменение (увеличение, ‘+’) количества элементов. Если впоследствии с полок было убрано пять книг, этот параметр также отражает изменение количества предметов, но в сторону уменьшения (значение символа «-«).
Если на полку не ставятся новые книги и не убираются старые, то число 0 оказывается индексом неизменного объекта.
Более того, понятие непротиворечивости используется не только в алгебре, но и в географии, истории, медицине и физике.
Положительные и отрицательные целые числа
Целые положительные числа — это числа, отмеченные символом «плюс». Например, к ним относятся. 2; 3; 4.
Отрицательные целые числа — это числа, обозначенные символом минус. Примеры: -1; -2; -3; -4.
Свойство нуля заключается в том, что он не принадлежит ни к положительным, ни к отрицательным числам. Разделите их.
Для каждого целого числа может существовать только одно противоположное отрицательное число. Обратное правило также применимо. Ноль — это его собственная противоположность.
Неположительные и неотрицательные целые числа
Неположительные целые числа — это отрицательные целые числа и нули. Например, эта группа содержит -54? -146; 0.
Целые неотрицательные числа — это целые положительные числа и нули. К ним относятся такие числа, как 54, 146 и 0.
Иначе, неположительные целые числа — это целые числа, меньшие или равные нулю. Напротив, неотрицательные целые числа — это целые числа больше нуля.
Эти термины были введены из соображений простоты. Чтобы не говорить, что число n меньше или равно нулю, фразу можно сократить и сказать: n — неположительное целое число.
Во-первых, запомните натуральные числа. Само название говорит о том, что это числа, используемые в естественных условиях для счета лет, отнимающих время. Чтобы охватить понятие полноты, необходимо расширить определение натуральных чисел.
Положительные и отрицательные целые числа
Из всех целых чисел целесообразно определить положительные и отрицательные целые числа. Приведем их определения.
Определение 2. Целые положительные числа
Целые положительные числа — это целые числа с положительным знаком.
Например, число 7 является целым числом с положительным, или положительным целым знаком. На прямой линии это число находится справа от точки отсчета. Это 0. Другие примеры целых положительных чисел — 12, 502, 42, 33 и 100500.
Определение 3: Отрицательные целые числа.
Отрицательное целое число — это целое число с отрицательным знаком.
Примерами отрицательных целых чисел являются. -528, -2568 и -1.
Число 0 разделяет положительные и отрицательные целые числа, а не положительные и отрицательные.
Противоположное число положительного целого числа по определению является отрицательным целым числом. Обратное также применимо. Противоположностью отрицательного целого числа является положительное целое число.
Другие определения отрицательных и положительных целых чисел можно сформулировать, используя сравнения с нулем.
Определение 4: Целые положительные числа
Положительное целое число — это целое число, большее нуля.
Отрицательное целое число — это целое число меньше нуля.
Следовательно, положительные целые числа лежат справа от начала координатной прямой, а отрицательные целые числа — слева от нуля.
Ранее мы говорили, что натуральные числа являются подмножеством целых чисел. Давайте уточним этот момент. Все целые положительные числа — это все целые положительные числа. Тогда все отрицательные целые числа — это общее количество чисел, противоположных натуральным числам.
Каждое натуральное число можно назвать целым, но не каждое целое число можно назвать натуральным. Отвечая на вопрос, являются ли отрицательные целые числа натуральными числами, можно сказать, что нет.
Неположительные и неотрицательные целые числа
Определение 6: Целые неотрицательные числа
Целые неотрицательные числа — это целые положительные и нулевые числа.
Неположительные целые числа — это отрицательные целые числа и нулевые числа.
Как видите, нулевые числа не являются ни положительными, ни отрицательными.
Примерами неотрицательных целых чисел являются 52, 128 и 0.
Примеры неположительных целых чисел: -52, -128, 0.
Неотрицательные числа — это числа, которые больше или равны нулю. Следовательно, неположительные целые числа — это числа, меньшие или равные нулю.
Термины «неположительные числа» и «неотрицательные числа» используются для краткости. Например, вместо того чтобы говорить, что число A — целое число, большее или равное нулю, мы можем сказать: A — целое неотрицательное число; A — целое неотрицательное число; A — целое неотрицательное число; и A — целое неотрицательное число.
Использование целых чисел при описании изменения величин
Зачем использовать интегральные числа? Во-первых, их можно легко использовать для описания и определения изменений в количестве объекта. Вот пример.
Предположим, что на складе имеется определенное количество осей коленчатого вала. Если на склад поступит еще 500 осей коленчатых валов, то их количество увеличится. Число 500 представляет собой изменение (увеличение) количества компонентов. Если со склада удаляется 200 компонентов, то количество осей коленчатого вала также называется изменением количества осей коленчатого вала. На этот раз курс направлен вниз.
Если со склада ничего не убрано и на нем ничего нет, то число 0 представляет собой неизменное количество принадлежностей.
Очевидное удобство использования целых чисел, в отличие от натуральных, заключается в том, что их запоминание четко указывает направление изменения цены (вверх или вниз).
Понижение температуры на 30 градусов может быть описано отрицательным числом (30), а целое число -2 может описать повышение температуры на 2 градуса.
Другой пример с использованием целых чисел показан ниже. Представьте, что на этот раз нам нужно предоставить пять монет. Тогда мы можем сказать, что владеем пятью монетами. Число 5 характеризует размер долга, а минус означает, что нужно отдать монеты.
Если мы должны две монеты одному человеку и еще одну монету трем людям, мы можем рассчитать отрицательный общий долг (5 монет).
Автор: Анастасия Лапина, ученица 6 класса Руководитель: Татьяна Геннадьевна Богоявленская школа
Основные виды
Существуют различные типы интегральных формул, которые можно использовать в расчетах. Основные из них следующие.
В некоторых задачах ответ необходимо округлить до ближайшего целого числа. Это означает, что оно заменяется выражением, более подходящим для данной серии. Если она изменяется в меньшую сторону, то это обозначается правилом Гаусса или Лежандра: x или e(x). Если его также необходимо округлить до большего значения, применяется функция «потолок». Дробную часть можно удалить или записать ближайшее целое число.
В любом случае, к истинному порядку можно подойти в разумной последовательности, которая объединяет его в целостное представление.
Цепные дроби или смежные дроби считаются лучшими инструментами для решения этой задачи. Например, числа необходимо анализировать: десятичная дробь 3,14159265 записывается как обычное и целое число -3, 22/7, 333/106, 355/113. Второе выражение, 22/7, является наиболее подходящим.
Интегральное выражение может быть неположительным и неотрицательным. Первая включает все отрицательные и нулевые значения, а вторая — все положительные. Ноль сам по себе не является ни положительным, ни отрицательным. Такие заявления используются для упрощения. Нет необходимости утверждать, что A больше нуля, достаточно просто указать, что оно неотрицательно. Простые примеры чисел согласованности для двух случаев: 0, 13, 28 и 0, -7, -24.
Описание изменения величин
Категория целых чисел используется для описания изменений различных величин. В частности, они используются для решения простых задач. На складе находится 400 насосов, вчера 300 были введены, а сегодня 200 были удалены. Остальные должны быть найдены. Если добавлено 300 элементов, пишется символ плюс: 400 + 300 = 700. Чтобы уменьшить число, поставьте минус перед числом: 700-200 = 500. искомое выражение — 500 насосов. Если движения товаров нет, то ноль означает, что количество не меняется.

Основное преимущество целочисленных значений перед натуральными ценами заключается в том, что они четко объясняют повышение или снижение цен. Его полезно использовать при описании температур. Мороз регистрируется по теплу в отрицательных и положительных числах.
Он также используется в финансовых расчетах. Если кто-то должен кому-то 10 долларов США, то сегодня у него -10 долларов США. Другими словами, долги могут быть записаны отрицательными числами, а положительные числа — прибылью. Общий долг также возникает через целые числа. Если вы должны заплатить 200 рублей за электроэнергию и 100 рублей за квартплату, ваш счет за коммунальные услуги составит -200 + (-100) = -300 рублей.
Применение в науках
Поняв, что такое математическое целое число, вы сможете увидеть, как оно используется. Этот тип номера используется во многих различных областях.

При изучении различных объектов природы некоторые данные описываются отрицательными и положительными числами. В этом случае он пригодится, если вам нужно создавать таблицы для финансовых отчетов и решать задачи с периодами времени, технологическими единицами и живыми объектами.
В физике малые квантовые числа используются для описания микромира. Все они являются целостными или полуколониальными. Затем для их решения были разработаны специальные математические методы: теория гетероморфных уравнений или целочисленное программирование.
Компьютерная наука также имеет дело с целыми числами. В этой области они используются как один из типов данных в языках программирования. Они преобразуются в фиксированные биты, один из которых кодирует синус, а другой — само число. Во многих современных компьютерах команды для действий представлены в целочисленной форме. Общая алгебра имеет четкую иерархию множеств. Натуральные числа входят в целые числа, которые входят в рациональные числа. Существуют также подлинные иррациональные выражения.
Множество чисел бесконечно. Существует столько же целых чисел, сколько и натуральных. Некоторые алгебраические структуры похожи на них: комплекс Гаусса и род Эйзенштейна. С целыми числами можно выполнять любые числовые действия, проводить проверки и учитывать изменения цен.








