При строительстве или проектировании жилищного строительства часто возникает необходимость построить углы, эквивалентные уже существующим. На помощь приходят стандарты и школьные знания по геометрии.
Построение биссектрис в треугольнике их свойство. Построение биссектрисы угла. Полные уроки — Гипермаркет знаний
Умение разбивать любой угол — это не только отличная математика. Эти знания чрезвычайно полезны для производителей, дизайнеров, инспекторов и портных. В жизни нужно уметь разделять многие вещи посередине.
В школе все выучили интересное определение: крыса бегает вокруг мыши, разделяя средний угол. Они назвали этого проворного и умного грызуна биссектрисой. Мы не знаем, как крысы делили углы, но для начинающих изучать школьный учебник «геометрии» мы можем предложить следующие методы.
На них влияют магнитные отклонения, которые зависят от их расположения на Земле. Они определяются на местности с помощью компаса. Как мы видели, инструменты, используемые для определения направления, — это угольник или переноска в направлении карты и компас в магнитном направлении. Следует отметить, что в представлении Гаусса-Крюгера направление отображения приближается к азимутальному углу автолинейной области. Азимут может быть вычислен путем измерения компаса на карте или носителя на карте, при условии внесения правильных поправок в девиацию и магнитную девиацию.
С помощью транспортира
Самый простой способ построения биссектрисы — использовать оборудование для измерения углов. На одной стороне угла следует прикрепить угломер, а опорную точку совместить с точкой O. Затем значение угла измеряется до градуса или радиуса и делится на два. С помощью того же долгого срока определите градус одной из сторон и проведите прямую линию, которая является биссектрисой к точке начала угла.
Возьмите компас и раздвиньте ноги до любого размера (в пределах границ рисунка). Начиная с начальной точки угла, проведите дугу вдоль луча и отметьте две точки. Назовите A1 и A2. Затем поочередно поверните компас к этим точкам и начертите две окружности любого диаметра (в масштабе чертежа). Их пересечения обозначены C и B. Далее следует биссектриса.
С помощью линейки
Для построения биссектрисы угла с помощью линейки необходимо определить точки A и B, получив лучи (стороны) равной длины. Затем нужно соединить их прямыми линиями и разделить с помощью линейки. Отрезок, взятый за середину, ставит точку С. Биссектриса приводит к гравировке прямой линии, проходящей через точки С и О.
Если измерительные инструменты отсутствуют, можно использовать логику. Нарисуйте углы на листе тоновой или простой плотной бумаги и аккуратно сложите лист так, чтобы лучи углов совпали. Линии сгиба на чертеже будут искомыми перегородками.
Проведите на чертеже прямую линию, соединяющую начальную точку с нужным пунктом назначения. Носитель помещается на меридиане так, чтобы центр или его продолжение находились над пересечением линий. Носитель поворачивается до тех пор, пока нуль не совпадет с северным направлением меридиана.
Основное свойство биссектрисы угла
На самом деле в бисекторе есть много свойств. И мы обязательно увидим их на следующем уроке. Но есть одна вещь, которую вы должны понять сейчас.
Теорема. — Это геометрическое положение точки, равной ребру определенного угла.
В математических терминах это означает два факта одновременно.
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте внесем ясность. Что называется расстоянием до стороны угла? Здесь можно использовать старое доброе определение расстояния точки от прямой.
Значение. — Это длина вертикали от определенной точки до данной линии.
Например, рассмотрим прямые $ l $ и $ a $, которые не лежат на этой линии. Нарисуйте вертикальную линию $ ah $ $ h \ in l $. Длина этой вертикали — это расстояние от $ a $ до прямой $ l $.
Поскольку один угол — это два луча, а каждый луч — часть прямой, расстояние до края угла можно легко определить. Это только два перпендикуляра: a
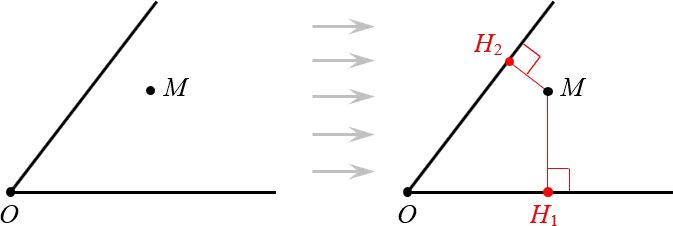
Определите расстояние от точки до стороны угла
Это! Теперь мы остаемся с вопросом: что такое расстояние? Таким образом, мы можем доказать основные свойства.
Как и было обещано, мы разделили квитанцию на две части.
Расстояния от точки на биссектрисе до сторон угла одинаковы
Рассмотрим произвольный общий угол $ o $ o $ и $ om $:.
Докажите, что именно эта точка $ m равна ребру угла.
- $\angle MO_>=\angle MO_>$ по условию (поскольку $OM$ — биссектриса);
- $\angle M_>o = \ угол m_> o = 90<>^\circ $ по построению;
- $\angle OM_>= \ угол om _> = 90<>^\circ -\angle MO_>$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Если расстояния равны, то точка лежит на биссектрисе
Теперь обратная ситуация. Пусть угол $ o и точка $ m на равных расстояниях от стороны этого угла.
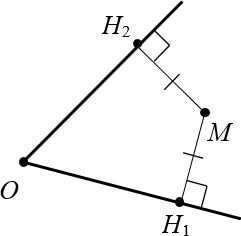
Докажите, что $ om $ является биссектрисой.
- Гипотенуза $OM$ — общая;
- Катеты $M_>=M_>$ по условию (ведь точка $M$ равноудалена от сторон угла);
- Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_^=OH_^=O^>-MH_^$.
Как видите, это несложно. Мы показали, что биссектриса угла — это геометрическое место знака, равного стороне этого угла.
Когда за плечами уже есть несколько сроков, пора переходить на следующий уровень. В следующем уроке вы рассмотрите более сложные свойства биссектрис и научитесь применять их в реальных задачах.
Помните, что в равностороннем треугольнике биссектрисы также являются медианами и высотами. Поэтому биссектриса может быть найдена простым делением вертикального падения противоположной стороны угла (высота) или этой стороны к центру и делением стыка средних точек на противоположный угол (интерстиций).
Биссектриса треугольника
Помимо угловых разбиений, существуют бисекторы треугольника, так как треугольник содержит три угла. Таким образом, каждый треугольник имеет три различных раздела.
Что такое биссектрисы треугольника? Биссектриса треугольника — это часть углового сечения, соединяющая вершину треугольника с противоположной точкой.
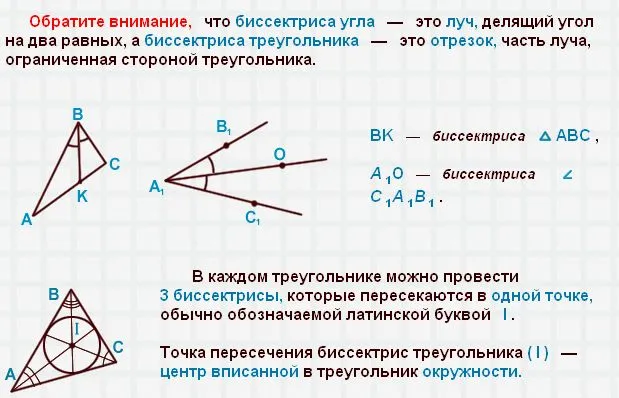
Биссектриса треугольника обладает несколькими уникальными свойствами. Например, он делит противоположную сторону на части, которые зависят от другой стороны.
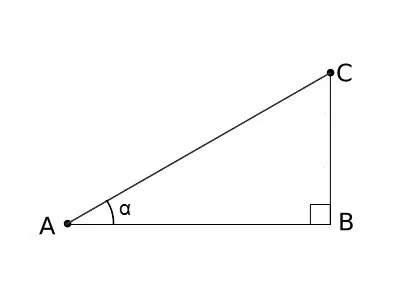
Для прямоугольного треугольника его кислородные биты при пересечении образуют угол 45°.
Ведь нельзя забывать о способности секущего треугольника пересекаться строго в центре окружности, записанной в треугольнике.
Самое интересное, что в случае равнобедренных треугольников прямые, проведенные к основанию, становятся биссектрисой, медианой и высотой. Аналогично, обратное правило гласит: если медиана, высота и биссектрисы, проведенные из одного верхнего треугольника, совпадают, то существует равнобедренный треугольник.
А какие свойства прямоугольного и равновесного треугольников вы помните?
Построение биссектрисы
Дихотомии углов производятся с помощью углов, использующих эту меру градуса. Чтобы начать построение прикуса, возьмите центральную градусную меру, положите половину угловой градусной меры на одну сторону вершины, а вторая половина будет биссектрисой угла.

Возьмите некоторый угол 90 градусов и биссектрисуйте его, чтобы получить два угла по 45 градусов.
Биссектриса делит угол на два прямых угла. Тупой угол делит окклюзию на два острых угла.
Из определения перегородки видно, что это радиус, который делит центральный угол. Чтобы откусить, уголок должен быть разделен посередине.
Алгоритм построения биссектрисы угла
1. сначала нарисуйте окружность вокруг вершины угла так, чтобы она пересекала стороны.
2.Далее измерьте расстояние между точками, в которых стороны угла пересекают окружность.

3. проведите два цикла с лучом так, чтобы пересечение находилось в пределах этого угла.

(4) Проведите радиус из вершины угла так, чтобы он проходил через точку пересечения этих циклов. Этот радиус является биссектрисой угла.
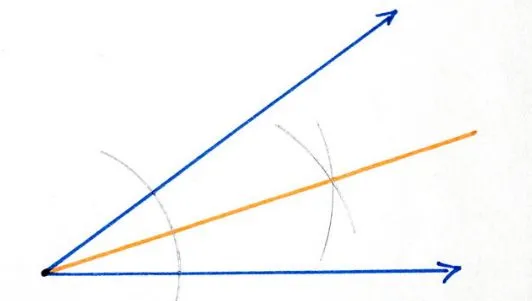
Теперь докажем, что этот радиус является биссектрисой угла. Рассмотрим пример двух треугольников с общими сторонами, то есть отрезками от вершины до пересечения окружностей.
Вторая пара соответствующих сторон — это отрезок, взятый в точке 1p. Она проходит от вершины угла до пересечения сторон.
Третья пара соответствующих сторон — это отрезки, взятые по 1п от пересечения цикла до пересечения окружности, соответственно, но полученные по 3п.
Таким образом, две пары этих частей равны, поскольку они являются лучами одного или двух циклов, но имеют одинаковый радиус. Установлено, что треугольники равны по всем трем сторонам. Хорошо известно, что когда треугольники равны, их углы также равны. Поэтому при вершине два новых угла и заданный угол равны, а сделанный радиус делится.
На конце компаса это направление «записывается». Если это модель, которая позволяет ей держаться курса. В случае с блюдцами весы уравновешены, и цена весов требуется системой нацеливания.
Полезные советы
В некоторых случаях для определения местоположения не обязательно использовать угольник и компас. Это возможно только в том случае, если необходимо триангулировать положение дихотомоса.
Полезные советы:.
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Даже дети в возрасте двух лет могут проектировать угловые перегородки с помощью компаса. Это требует очень мало времени, знаний и усилий. Подробно изучив этот процесс, каждый ученик сможет легко разделить любой угол на центральный угол и объяснить этот процесс своим одноклассникам.
Из вершины угла проведите радиус от точки пересечения окружностей. Если есть два пересечения окружности, необходимо пройти через оба. Полученный радиус является биссектрисой этого угла.
Как построить биссектрису угла

Слово «биссектриса» переводится французами как «деление на два». Биссектриса угла — это «равновеликий делитель» угла, т.е. деление центрального угла.
Угловой дикотер. — Радиус оттягивается от вершины угла между его сторонами, разделяя центральный угол.
Угловые дикотеры могут быть разработаны путем измерения градуса одного угла в течение длительного периода времени. Для этого измерение градуса определенного угла производится по центру, а измерение половины угла — от вершины к одной из сторон. Вторая сторона такого угла является биссектрисой этого угла.
Если данный угол равен 60°, то два угла, образованные отрезком, равны 30° каждый, так как 60° : 2 = 30°.
Широкий угол делится прикусом на два правильных угла (180°:2 = 90°), а каждый тупой угол делится прикусом на два острых угла.
Построение биссектрисы угла с помощью циркуля и линейки
- Из вершины угла, любым радиусом, необходимо провести дугу окружности, чтобы она пересекла стороны угла
- Из каждой точки (их две) пересечения дуги и стороны угла, снова провести души окружности (другим радиусом)
- Через любую из точек пересечения дуг дополнительно построенных окружностей, провести луч из вершины угла, который и будет биссектрисой этого угла
Треугольное деление треугольника является частью биссектрисы угла, простирающейся от вершины угла до его пересечения с противоположной стороной.
Треугольник имеет три биссектрисы из каждой вершины.
Биссектрисы углов треугольника обладают рядом особых свойств, которые описаны в другой статье «Биссектрисы углов треугольника».
В треугольниках ABC внешние биссектрисы, то есть биссектрисы углов, прилегающих к внутренним углам треугольника, можно разделить, за исключением внутренних или простых биссектрис. Внутренняя и внешняя биссектрисы одного и того же угла перпендикулярны. Дополнительные сведения см. в разделе Биссектриса внешних углов треугольника.
Что такое биссектрисы треугольника? Биссектриса треугольника — это часть углового сечения, соединяющая вершину треугольника с противоположной точкой.
Презентация по геометрии на тему «Построение биссектрисы угла» (7 класс)
Отметим, что в соответствии с федеральным законодательством в организациях, осуществляющих образовательную деятельность, согласно «273-ФЗ Об образовании в Российской Федерации», обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется как совместно с другими обучающимися, так и отдельными классами или группами.


Курсы повышения квалификации
Основы общей и педагогической психологии в деятельности педагога образовательного учреждения

Курсы повышения квалификации
Особенности подготовки к сдаче ЕГЭ по математике в условиях реализации ФГОС СОО
Курсы повышения квалификации
Методика преподавания математики в среднем профессиональном образовании в условиях реализации ФГОС СПО

«Особенности изучения математики с учащимися с ОВЗ»
Рабочие листы и материалы для учителей и
Более 2 500 образовательных ресурсов для школьного и домашнего обучения
Описание презентации по отдельным слайдам:

Построение частей угла
Автор: В. Чечко, профессор математики гимназии № 10 г. Новокузнецка A B C M

Радиус, начинающийся от вершины угла, проходит через его стороны и делит угол на две части.
Что называется биссектрисой угла? Угловой дикотер — это… a b c m.
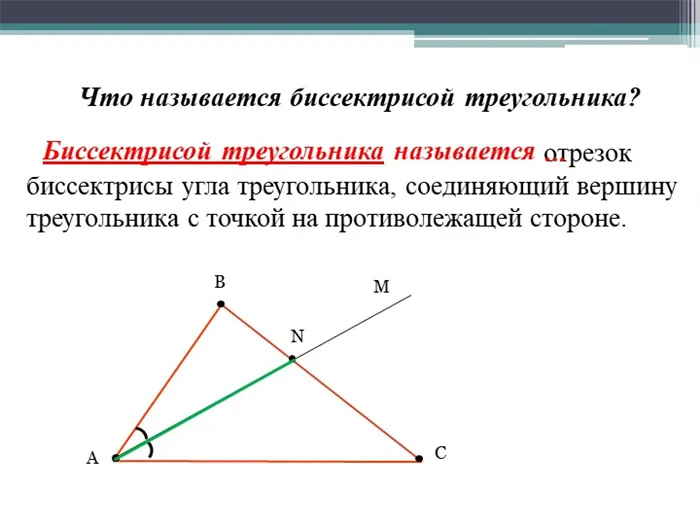
Что называется угловым двутавром треугольника? Биссектрисы углов треугольника соединяют верхнюю часть треугольника с противоположными точками.
Биссектрисы треугольника — это … 1. называется a m b c n
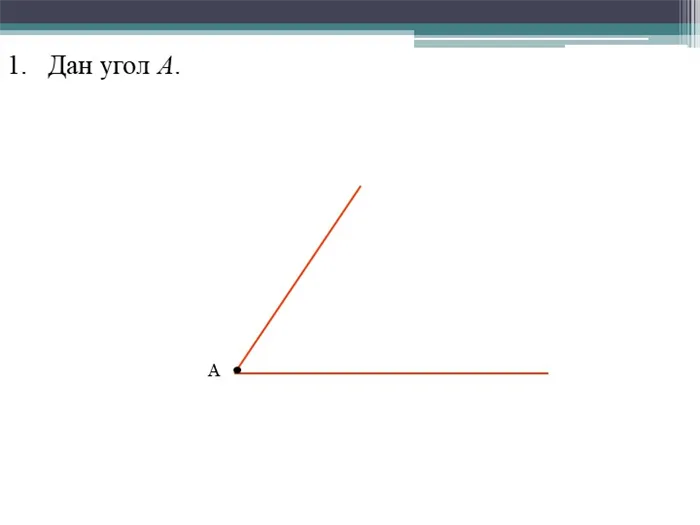
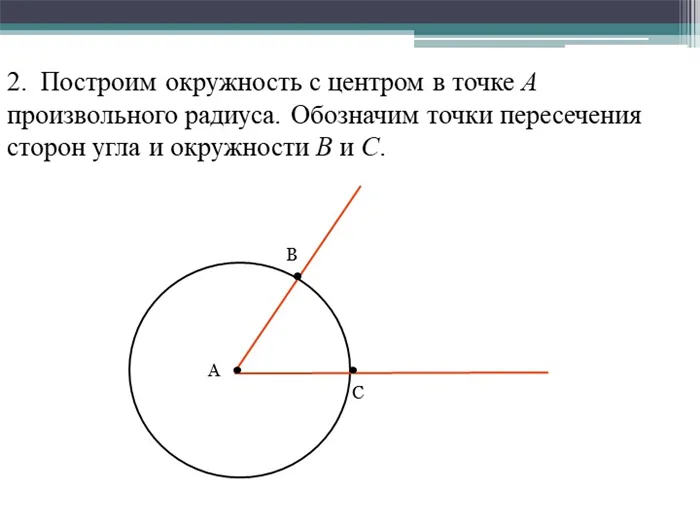
2. постройте окружность любого радиуса с центром в точке A. Символы для пересечения сторон угла и циклов B и C
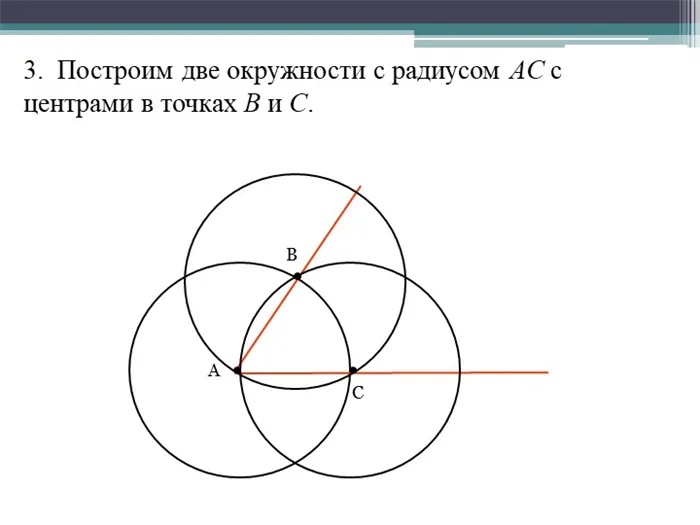
3. постройте две окружности с радиусами AC и центрами в точках B и C. ABC
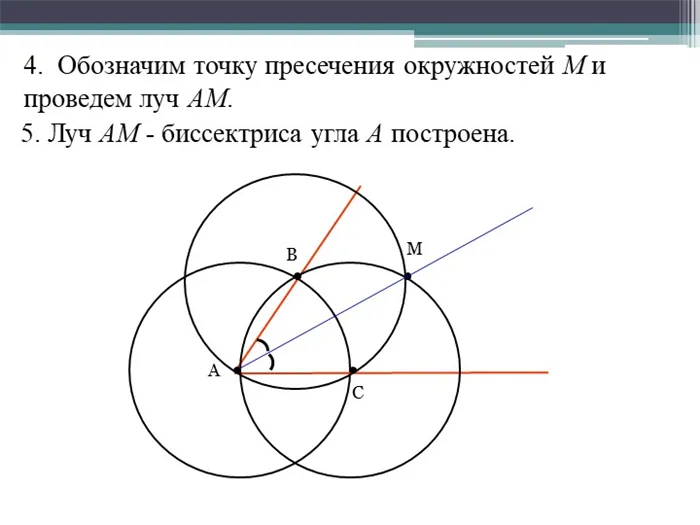
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 913 899 Материал основания.
‘Интеграция современного искусства в детское творчество’
Сертификат и скидка для каждого участника
Ищем преподавателей в команду Infowork
Другие материалы
‘Практический подход к решению проблемы потери смысла жизни: логопедическая и языковая терапия’.
Сертификат и скидка для каждого участника
Вам будут интересны эти курсы:
- Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
- Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
- Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
- Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
- Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
- Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
- Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
- Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
- Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
- Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
- Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Оставьте свой комментарий
- 09.01.2016 3647
- PPTX 63.4 кбайт
- 125 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Данный ресурс опубликован Вероникой Иванец. Инфоурок является информационным посредником и предлагает пользователям возможность публиковать на сайте методические материалы. Пользователи, загружающие материалы на сайт, несут полную ответственность за них и содержащуюся в них информацию, а также за соблюдение авторских прав.
Если вы считаете, что материал нарушает авторские права или должен быть удален с сайта по любой другой причине, вы можете подать жалобу на материал.
Автор материала
- На сайте: 6 лет и 5 месяцев
- Подписчики: 0
- Всего просмотров: 10005
- Всего материалов: 8
Московский институт профессиональной подготовки и повышения квалификации преподавателей








