Арифметическая прогрессия что такое. Арифметическая прогрессия что такое

Эквипропорциональная последовательность — это ряд чисел, в котором каждый член начинается со второго и равен предыдущему члену, умноженному на одно и то же число q. Это знаменатель прогрессии. Элементы экви-пропорциональной последовательности могут быть заданы следующим образом.

Прогрессии и последовательности: решаем ОГЭ по математике

Вопросы GCSE по «эволюции» тесно связаны с понятием «последовательность». Если ученики понимают, как числа в последовательности связаны друг с другом, они хорошо справятся с домашним заданием. Здесь мы рассмотрим один из самых сложных предметов в GCSE Maths — прогрессию. Примечание: Данный ресурс содержит все необходимое для решения GCSE без воды.

Слишком часто мы сталкиваемся с математическими последовательностями и событиями в нашей жизни буквально каждый день, не осознавая этого. Однако такая встреча не всегда приятна, особенно если она происходит во время инспекции.

Последовательность — это набор элементов множества, который удовлетворяет следующим условиям

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Вы хотите остепениться и подготовиться к сдаче GCSE? MAXIMUM готов помочь! Все наши учителя сдали экзамены с хорошими оценками. Мы ежегодно изучаем изменения в FIPI и соответствующим образом адаптируем наши курсы. Узнайте больше о наших курсах и выберите подходящий!

Что такое арифметическая прогрессия?

Взгляните на следующую серию рисунков.

Какую аудиторию они могут иметь? Во-первых, все они являются нечетными числами, тогда каждое последующее число можно получить из предыдущего путем прибавления одного и того же числа. Назовем это число d. В данном случае d=2.

Приведенная выше последовательность называется эквидифференциальной последовательностью. Дайте определение.

Приведем основное уравнение:.

Сумма первых n членов последовательности может быть рассчитана по следующей формуле

Числовой прогресс также имеет отличительные свойства.

Как решать задачи ОГЭ на арифметическую прогрессию?

Теория — это прекрасно, но все теоретические вопросы должны применяться на практике. Сейчас мы рассмотрим некоторые вопросы GCSE по числовой прогрессии.

Например, в GCSE вы можете встретить следующие работы

Вот это да! Мы успешно выполнили первый прототип задания, с которым мы можем столкнуться на реальном экзамене. Мы добиваемся прогресса.

Это! Формула для суммы прогрессий для первых n членов приведена в справочном материале по тесту, поэтому в ней нет ничего сложного.

Конечно, мы можем сложить все значения вручную, но что если нам нужно найти сумму ɑ (ɑ displaystyle 100 \) для данного члена в задаче, как это делал Гаусс?

Формулы n –го члена арифметической прогрессии

Выражение для n-го члена экви-дифференциальной последовательности (a_n ), что первый член₁ Разница составляет d: d

а _n = a₁ + d(n – 1).

Формула содержит четыре переменные. Если вы знаете значения трех из них, вы также можете вычислить значение четвертого. Убедитесь в этом, решив следующие четыре задачи (в каждом случае определите известные переменные, чтобы получить ответ): d

1. В арифметической прогрессии а₁ =2 и d=3. Найдите одно из них.₆₅. (Ответ: 194.)
2. В арифметической прогрессии а₈₆ =100 и d=-4. Найдите одну₁. (Ответ: 440.)
3. В арифметической прогрессии а₁ =65 и₂₁ = – 55. Найдите d. (Ответ: – 6.)
4. В арифметической прогрессии а₁ = 1 и d=4. Найдите номер члена, равного 397. (Ответ: 100.)

Пример 4. Дана эволюция чисел: 1.5, 4.5, 7.5, 10.5, ….. Каково количество членов в последовательности, начиная с 1000 и больше?

В данной разработке.₁ =1,5 и d=4,5 —1,5 =3. Запишите выражение для n-го члена._n = 1,5 + 3 (n —1), т.е. a_n = 3_n —1,5.

Найдите значение n. В этих условиях_n > 1000. Для этого решите неравенство 3n —1,5> 1000, n> 333. Таким образом, членов в этой прогрессии больше 1000, начиная с условия, что число равно 334. 1₃₃₄Примечание: Есть один.₃₃₄ (= 3-334-1.5 = 1000.5).

Способ 1. Выразив а₁₅ и один.₂₀ От одного.₁ и d, составим систему уравнений:

Решив его, получаем.₁ = 138, d = -7. (Найдите этот результат самостоятельно.) Используя уравнение для n-го члена₃₀, a is: a₃₀= 138-7-29=-65.

Метод 2. выразить один₂₀ Множественные.₁₅ и г: а₂₀ = a₁₅ +5d. Подставьте значения₂₀ и один.₁₅, имеем: 5 = 40 + 5d, следовательно, d = -7. Теперь находим₃₀. Это можно сделать, например, следующим образом.₃₀ = a₂₀ + 10d = 5-7-10 = -65.

Второй метод основан на следующем утверждении_n является числовой последовательностью и для всех натуральных n и m

а_n = a_m + ( n – m)d.

Если вы забыли это выражение, в любом случае вы можете выразить одну прогрессию в терминах другой, выполнив простое преобразование. Например, выразим одно₂₀ Множественные.₅: а_{2 0} = a₁ + 19d = (a₁ +4δ) + 15δ = α₅ + 15d.

Изображение членов арифметической прогрессии точками на координатной плоскости

Термины числовой последовательности могут быть представлены точками на координатном уровне. Для этого на горизонтальной оси указывается номер члена, а на вертикальной оси — соответствующий член последовательности.

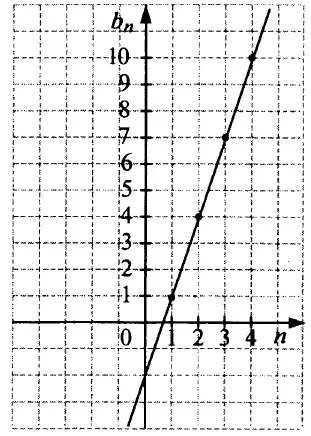
Если последовательность является эквидифференциальной, то точка, обозначающая член, лежит на прямой. Важно отметить, что n-й член числовой прогрессии зависит от количества членов n. На практике: если

a_n = a₁ + d(n-1) = d_n + (a)₁ – 1).

Например, для числовой прогрессии₁ = 1 и d = 3, тогда a_n = 1 + 3 (n-1), т.е. a_n = 3n-2; поэтому точка, обозначающая член этой прогрессии, лежит на прямой y = 3 x-2 (см. график).

Условия численной прогрессии варьируются в равной степени. На каждом шаге вдоль горизонтальной оси эти точки увеличиваются или уменьшаются на одно и то же количество единиц вдоль вертикальной оси.

Формулы суммы первых n членов арифметической прогрессии

Если известны первый и последний из суммируемых членов, то удобно пользоваться формулой

Пример 6: Найдите сумму всех натуральных чисел от 1 до 1000.

Слагаемые в сумме 1 + 2 + 3 + … + 1000 образуют арифметическую прогрессию. Подставив в формулу суммы а₁ = 1, a_n = 1000, n = 1000, получим:
Формулу суммы первых n членов арифметической прогрессии можно записать в другом виде, выразив S _n От одного.₁, d и n :

Пример 7: Найдите сумму всех двузначных чисел, делящихся на три.

Последовательность 12; 15; 18; … ; 99 является арифметической прогрессией, в которой а₁ = 12, a_n = 99, d = 3. Найдите номер последнего члена. Подстановка в формулу a_n = a₁ + d(n – 1) указанные значения, получим уравнение 99 = 12 + 3( n – 1). Решив его, найдём, что n = 30. Теперь можно вычислить искомую сумму:

Это обзор математики «численного прогресса». Выберите следующий шаг.

Присваиваемый номер уникален для одного номера в последовательности. Это означает, что в последовательности нет 3-секундных номеров. Второе число (например, ⌘ (⌘ displaystyle n \)-число) всегда равно 1.

п.3. Свойства арифметической прогрессии

Свойство 1. линейность

Арифметическая прогрессия — это линейная функция f(n) = kn + b:.

Угловой коэффициент k = d и свободный член b = a₁ -d.

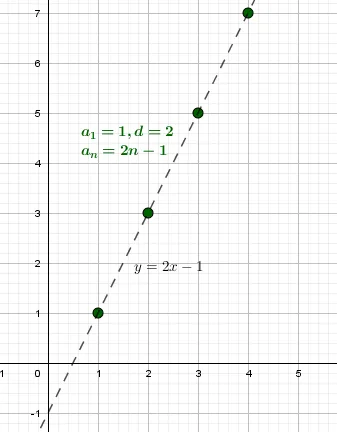
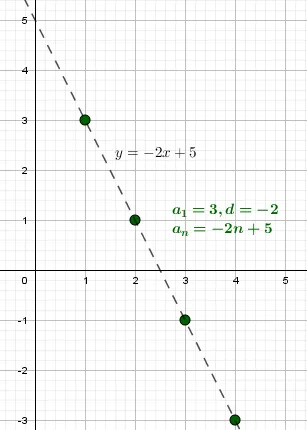
Результат: любая числовая последовательность может быть задана формулой $\mathrm.< a_n=dn+b,\ \ n\in\mathbb,\ \ b\in\mathbb,\ \ d\in\mathbb> $, где d и b — целые числа.

Свойство 2. Доказательство численного прогресса.

Для того чтобы числовая последовательность была арифметической прогрессией, необходимо и достаточно, чтобы каждый член, начиная со второго, был средним арифметическим предыдущего и последующего. $ \ mathrm< \left\- \text\ \Leftrightarrow\ a_n=\frac+a_>,, \ \ \ \ n \ в \ mathbb, ⢙ \ \ n \ geq 2 >> $ Результат: каждый член прогрессии является средним арифметическим двух равноудаленных от него членов: $ \ mathrm< a_n=\frac+a_>\ \ \ \ n \ в \ mathbb, \ \ \ n \ в \ mathbb, \ \ \ n \ geq k + 1> $

Пример: поиск одного₉Если мы это знаем.₇ = 10, a₁₁ = 15 от результата знака экви-дифференциальной последовательности: ס (ס mathrm> = \ frac = 12,5> \)

Свойство 3. Эквивалентность сумм индексов

Если n> является арифметической прогрессией, равенство сумм индексов вытекает из равенства сумм членов. $ \ mathrm< m+k=p+q \Rightarrow a_m+a_k=a_p+a_q >Результат: сумма членов, равноудаленных от края прогрессии, постоянна: $ \ mathrm< a_1 + a_n=a_2+a_=a_3+a_=. > $

Пример: поиск одного₆Если мы это знаем.₂ = 5, a₄ = 10, a₈ = 20, если сумма индексов равна a₂ + a₈ = a₄ + a₆ где.₆ = a₂ + a₈ -a₄ = 5 + 20-10 = 15

п.4. Сумма первых n членов арифметической прогрессии

Сумма первых n членов эквидифференциальной последовательности равна произведению среднего арифметического ее крайних значений и числа членов. $ \ mathrm.< S_n=\fracn> $

Пример: найдите сумму первых 100 целых положительных чисел: 1+2+. + 100 В этом случае.₁ = 1, a₁₀₀ = 100, n = 100 \ (⌘ mathrm< S_=\frac\cdot 100=5050>\)

п.5. Примеры

Пример 1. Найдите разность между первым членом и числовой прогрессией в следующих случаях.₇ = 10, a₁₅ = 42 Найдите разность между этими терминами.₁₅ -a₇ = (a₁ + 14d) — (a₁ + 6d) = 8d получена разность хода: 42 — 10 = 8d => d = 32: 8 = 4 Термин 7: a₇ = a₁ + 6d = a₁ +6-4 = 10 => a₁ = 10-24 = -14 Ответ: a₁ = -14, d = 4

б) один.₁₀ = 95, s.₁₀ = 500 Эволюционная сумма: ס (ס mathrm = \ frac> \ cdot 10 \ Rightarrow 500 = (a_1 + 95) ס cdot 5 \ Rightarrow a_1 + 95 = 100 \ Rightarrow a_1 = 5> \) Раздел 10: ס (ס mathrm = a_1 + 9d \ Rightarrow95 = 5 + 9d \ Rightarrow 9d = 90 \ Rightarrow d = 10> \) Ответ: a₁ = 5, d = 10

Пример 2.Найдите сумму первых 100 нечетных целых положительных чисел. Какова окончательная сумма этого итога? Найдите сумму \ (⌘ mathrm<\underbrace<1+3+5+. >_> \) путем гадания.₁ = 1, d = 2, n = 100. из этого следует, что \(⌘ mathrm = \ fracn = \ frac \ cdot 100 = 10000> \) Формула для n-го члена этой прогрессии: ⌘(⌘ mathrm \) 100-й член ⌘(⌘ mathrm = 2 \ cdot 100-1 = 199> \) Ответ: s₁₀₀ = 10000,.₁₀₀ = 199

Пример 3*. Количество членов 10, 16, 22, в экви-дифференциальной последовательности. Они находятся между числами 110 и 345? Условия являются одними из.₁ = 10, d = 16-10=6 Выражение a для n-го члена данной прогрессии_n = a₁ + d(n-1) = dn + (a₁ -d) = 6n + 4 Определенные числа могут быть членами определенной серии или соседними с ними. Замените их в формуле для n-го члена: ⌘ begin \ mathrm< 6k+4=110\Rightarrow 6k=106\Rightarrow k=17\frac23\Rightarrow 17\lt k\lt 18 >\\\\ mathrm< 6m+4=345\Rightarrow 6m=341\Rightarrow m=56\frac56\Rightarrow 56\lt m\lt 57 >\ Ближайший правый сосед Јend100 — 1₁₈ = 6-18 + 4 = 112, левым ближайшим соседом k =18345 является₅₆ = 6-56 + 4 = 340, m = 56 Количество членов, прогрессирующих с заданным интервалом:.

n = m-k + 1 = 56-18 + 1 = 39

Пример 4. Одиннадцатый член в последовательности экви-дифференциала равен 7. Найдите сумму первых 21 члена. Из свойств суммы индексов: a₁₁ + a₁₁ = a₁ + a₂₁ где.₁ + a₂₁ = 2a₁₁ = 14 Сумма искомых денег: ⌘ (⌘ mathrm = \ frac> \ cdot 21 = \ frac \ cdot 21 = 147> \) Ответ: 147

Пример 5. Углы выпуклого пятиугольника образуют числовую прогрессию. Найдите третье условие прогрессии. Сумма углов выпуклого пятиугольника S₅ = 180°- (5-2) = 540° Если углы образуют числовую прогрессию, то. $ \ mathrm.< S_5=\frac\cdot 5=540^\circ\Rightarrow a_1+a_5=216^\circ > Как сумма показателей $: a₃ + a₃ = a₁ + a₅ Откуда: \(\mathrm\) Ответ: 108°

Пример 6.При каких значениях x числа x 2-11, 2x 2 + 29 и x 4-139 в этой последовательности являются частью равновероятной последовательности? Для последовательных членов получаются следующие уравнения

a₂ -a₁ = a₃ -a₂ (2x 2 + 29) — (x 2-11) = (x 4 — -139) — (2x 2 + 29) x 4-3x 2 —208 =0⇒ (x 2 + 13) (x 2-16) = 0⇒ x2 = 16⇒ x = ±4

Пример 7.Сумма первых трех членов в убывающей последовательности равенств равна 9, а сумма их квадратов равна 99. Найдите седьмой член в прогрессии. d по контракту.< 0 и: $ \left\< \begin < l >\ mathrm&\ \ mathrm&\ end

ight. используя свойство эволюции: ⌘ (⌘ mathrm> \). Из первого уравнения имеем._nn

Формула n-го члена арифметической прогрессии

.

Значит,

Определение равноотстоящей последовательности показывает, что равенство истинно.

Перевод с языка формул на русский: если известна разность между первым членом и последовательностью равенств, то можно найти произвольный член.

Если известны первый член и разность, то можно определить числовую последовательность._n = a₁ = a

Формулы арифметической прогрессии

+ d * (n —1) называется выражением для n-го члена экви-дифференциальной последовательности.

В 9 классе мы рассмотрим все уравнения последовательности экви-дифференциала. Давайте посмотрим, как это дается:._nn_nn

:.

Тип для нахождения суммы n членов эквидифференциальной последовательности:.

Чтобы быстрее запомнить формулы, вы можете использовать эту таблицу вместе с основными определениями.

Рассмотрим пример экви-дифференциальной последовательности._nn₁), где n

= 0 и d = 2.

Найдите: первые пять периодов прогресса и десятый период прогресса.

Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:

Решите последовательность экви-дифференциалов:.

a₁₀ = a₁ = a

Геометрическая прогрессия

+ 2 * (10-1) = 0 + 2 ⋅ 9 = 18._nn

), каждый последующий член может быть найден путем умножения предыдущего члена на то же число q._nn

Общий член эквипропорциональной последовательности bn можно рассчитать по формуле) является равнопропорциональной последовательностью, то для всех натуральных значений n имеет место следующее соотношениеn + 1n * q, где q — знаменатель геометрической прогрессии

n_nn₁) первый член b

Если знаменатель q известен, то прогрессию можно проверить.

Общий член эквипропорциональной последовательности bn можно рассчитать по формуле_nn + 1₁ = b₁ * q n-1, где n — индексный член члена прогрессии, b

— первый член прогрессии, а q — знаменатель.

Примеры 1,2, 6, 18, 54, … -геометрическая эволюция b = 2, q = 3.

Пример 2.3, -3, 3, -3, … -геометрическая эволюция b = 3, q=-1.

Пример 3.7, 7, 7, 7, 7, 7, … -геометрическая эволюция b = 7, q=-1.

Арифметическая прогрессия.

Определения и обозначения.

Примечания. Самый простой способ перейти от десятичных чисел к обычным дробям — это прочитать число, разделить его на дробь и записать. Например, «и 3 мм» — это то же самое, что и \ («+ \ dfrac» \)._nn

>, где каждый член, начиная со второго, равен предыдущему члену, к которому добавляется одна и та же константа для данного порядкового номера d. Число d называется разностью эквидифференциальной последовательности.

Разность d числовой прогрессии может быть как положительной, так и отрицательной. В первом случае каждый последующий период прогрессии на одно равное число больше предыдущего, во втором — на одно равное число меньше предыдущего. Например.

2; 4; 6; 8; 10; 12; 14; 16; 18.18. -Увеличивающаяся последовательность одинаковых чисел (d = 2),.

Свойства арифметической прогрессии.

17; 14; 11; 8; 5; 2; -1; -4; -7. -Уменьшение изометрической последовательности (d = -3).

\ (a_ = a_n + d; \; a_ = a_n —d; \) ⌘ (a_n = a_k + d \ cdot(n-k). \)

Примеры задач на арифметическую прогрессию.

Таким образом, экви-разностная последовательность полностью определяется двумя параметрами первого члена и разности.

Задача 2. Напишите несколько последовательных членов последовательности тождеств: … ; 11; vat; -13; -25; …. Найдите период прогресса, обозначенный x.

Метод I. Известны предыдущий и следующий члены прогрессии элемента x. Используйте атрибут арифметического свойства ⌘a_n= \ frac + a _>; \ x = \ frac = \ frac = \ frac=-1. \Ј Метод II: Нахождение разности между двумя соседними известными членами прогрессии Ј d = -25- (-13) = -25 + 13 = -12. Согласно определению последовательности равенств, такая же разность существует между элементами x и direct. Поэтому его сосед

\(x = -13 -d = -13-(-12)⌘)⌘(= -13 + 12 = -1 \) или ⌘(x = 11 + d = 11 + (-12)⌘)⌘(= 11-12 = -1.)₁ Вопрос 3. Последовательность чисел задана условием a._{) является равнопропорциональной последовательностью, то для всех натуральных значений n имеет место следующее соотношение}n + 1_nn

Искомую сумму можно найти по формуле \(S_n = \dfrac\cdot n\), т.е. \S_ = \frac\cdot 14 = (a_1+a_)\cdot7.\ Значение первого члена прогрессии известно a ₁ —17. Найдите сумму первых 14 членов._{) является равнопропорциональной последовательностью, то для всех натуральных значений n имеет место следующее соотношение}n + 1_nn

-17. Это указывает на то, что каждый последующий период прогрессии (n + 1-й) на 17 меньше текущего (9-го) периода. Другими словами, разница в прогрессии d = -17. Поэтому 14-й период прогрессии можно найти по формуле ⌘ (a_n = a_1 + d \ cdot(n-1)⌘).

\(a_ = a_1 + d \ cdot(14-1)ǫ)ǫ (= 44 + (-17)ǫ cdot13 = 44 -221 = —177).

Геометрическая прогрессия.

Определения и обозначения.

\ cdot7 \ cdot7 = (a_1 + a _)\ cdot7 = (44 + (-177)\ cdot7 = -931.\ cdot7 = -931.\ cdot7 = -931.\ cdot7 = -931.\ cdot7 = -931.\ cdot7 = -931._nn

>0. Первый член ненулевой, и каждый член второго члена получается умножением предыдущего члена на константу с таким порядковым номером q≠0. Это число является знаменателем геометрической прогрессии.< q < 1, то в однаковое число раз меньше предыдущего. А если знаменатель прогрессии отрицателен, то последовательность окажется знакопеременной. Например:

В знаменателе геометрической прогрессии q может стоять любое рациональное число, отличное от нуля. Если q> 1, то каждый последующий период прогрессии имеет тот же номер, что и предыдущий, если он равен нулю.

2; 4; 8; 8; 16; 16; 32; 64; 128; 256; 512. — Увеличение геометрической эволюции (q = 2). Каждое последующее число в два раза больше предыдущего.

17; 8,5; 4,25; 2,125; 1,0625; 0,53125; 0,265625. -Убывающая геометрическая эволюция (q = 1/2 = 0,5). Каждое последующее число равно половине.

Свойства геометрической прогрессии.

1; -3; 9; -27; 81; -243; 729. -Геометрическая эволюция (q = -3).

Таким образом, экви-пропорциональная последовательность полностью определяется двумя параметрами, первым членом и знаменателем.

Бесконечно убывающая геометрическая прогрессия

Заметим, что в общем случае все последовательности бесконечны. Однако в задачах мы часто встречаем упорядоченные конечные части таких множеств. Это также называется последовательностью и продвижением.< 1 существует сумма В случае бесконечно убывающей последовательности равных пропорций это знаменатель аванса q |все

Условие._nn

Примеры задач на геометрическую прогрессию.

n варьируется от 1 до бесконечности._nn

> \ b_3 = \ frac, ⌘; b_6=196. найдите знаменатель ⌘ прогрессии.

Используя соотношение ⌘ (b_n = b_k \ cdot q ^, ⌘), подставьте известные величины и решите простое уравнение относительно неизвестных.

\ (b_6 = b_3 \ cdot q ^ \\\\\ 196 = \ dfrac \ cdot q ^ 3 \ cdot q ^ 3 = 196 \ cdot \ dfrac = \ dfrac = \ 49 \ cdot7 = 7 ^ 3. \ cdot q ^ 3 = 7 ^ 3; \; q = 7. \)_nn

>, \(b_1 + b_2 = 4 \) и \(S = \ dfrac \).

Каждый член прогрессии может быть найден по формуле для его общего члена. То есть используются первый член и знаменатель. Таким образом, запрос «найти прогресс» эквивалентен запросу «найти первый член прогресса и его знаменатель».

Из первого члена, используя выражение \(b_2 = b_1 \ cdot q \), получаем \ b_1 + b_2 = b_1 + b_1 \ cdot q = 4 \ b_1 \ cdot (1 + q) = 4 \ b_1 =\frac \᥉Найдите сумму всех выполняемых членов. Это ἀ (ἀ dfrac, ἀ) по формуле ἀ (S = ἀ dfrac ἀ). Замените это соотношение на \(b_1 \) и составьте уравнение для определения неизвестного знаменателя прогрессии.

Решите уравнение ⌘frac= \ frac- \ cdot3 = 16 \ cdot(1-q ^ 2)-ዄ 12-16 = -16q ^ 2- \ q ^ 2 = \ frac = \ frac- \ q = \ pm \ frac.ዄ Следовательно, две последовательности удовлетворяют следующим условиям.<3\cdot 2^>\)

\ dfrac = \ dfrac- \ dfrac- \ dfrac- \ dfrac- \ cdot)

Ответы и решения на эти вопросы временно скрыты. Для их просмотра используйте соответствующие кнопки. Но сначала попробуйте решить проблему самостоятельно.

Задача 10. В каждый день рождения родители Саши кладут в его копилку столько же монет, сколько ему лет. В настоящее время в копилке 21 монета. Сколько тебе лет?

На каждый день рождения Саша копит еще один год, в результате чего в копилку попадает еще одна монетка. Таким образом, мы имеем дело с возрастающей последовательностью одинаковых чисел. Разница составляет d = 1. Первый день рождения Саши, очевидно, праздновался, когда ей исполнился год, поэтому первый член в прогрессии \(a_1 = 1 \).₁Поскольку копилка содержит все «накопленные» монеты, их количество является суммой всех годовых вложений, то есть числовой прогрессией. Замените сумму уравнения всеми известными данными в формуле и решите уравнение относительно неизвестных параметров. Используйте уравнение суммирования в следующем виде \(S_n = \ dfrac \ cdot n.}) \ 21 = \ frac \ cdot n \ 21 = \ frac \ 42 = 2n + n ^ 2-n \ n ^ 2 + n —42 = 0 Решение этого квадратного уравнения дает корни n₂ = -7 и n

= 6. Саша, очевидно, не является отрицательным числом лет, поэтому рассмотрим корень n = 6.

Чеки. При выполнении таких важных задач, как тестирование, рекомендуется по возможности проводить проверки. Если окажется, что Саша недостаточно большой, вы можете «вручную» добавить все монеты в копилку в течение шести лет. 1 + 2 + 3 + 4 + 5 + 6 = 21. их общая сумма фактически равна 21. Это означает, что проблема решена правильно.

Вопрос 11.Вася и Петя готовились к экзамену. Они решили все задачи в сборнике, и каждый решил все задачи в сборнике ровно за семь дней. В первый день Вася решил пять задач, а затем каждый день решал на одну задачу больше, чем накануне. Если Васе, чтобы дотянуться до Васи, нужно каждый день решать на две задачи больше, то сколько задач решил Петя в первый день?

Оба мальчика каждый день решали задачи, увеличивая свои числа на одно и то же число. Это экви-дифференциальная последовательность. Граф Васина хорошо известен: \(a_1 = 5 \) и \(d = 1 \). Зная, что Вася решил все задачи за семь дней, мы можем найти общее количество задач в сборнике S_7 = \ frac \ cdot7 \ a_7 = a_1 + d(7-1) = 5 + 1 \ cdot6 = 11 \ S_7 = \ frac \ cdot7 = 56 \ поэтому В сборнике 56 задач, которые Вася тоже решил за семь дней. Опять же, мы используем уравнение для суммы последовательности экви-дифференциалов, но создаем уравнение для \(a_1 \). Разность хода известна d=2.\ S_7 = \ frac \ cdot7 \ a_7 = a_1 + d(7-1) = a_1 + 2 \ cdot6 = a_1 + 12 \ S_7 = \ frac \ cdot7 = (a_1 + 6 ) \ cdot7{ решить уравнение Lo_7a_1+42 = 56 \ cdot7 = 14; \ —a_1 = 2. \

Часть условия задачи «каждую следующую. на 5 меньше» подсказывает, что имеем дело с арифметической прогрессией: \(a_1=400, d = -5\). Для определения расстояния, которое пробежал спорсмен за тренировку в целом, нужно сложить участки, пройденные в каждую из 30 минут. Используем формулу суммы арифметической прогрессии. \S_ = \frac\cdot30 \\ a_ = a_1 + d(30-1) = 400 — 5\cdot29 = 255\\ S_ = \frac\cdot30 = (400+255)\cdot15 = 9825 (м) = 9,825 (км) \ 9,825 километра составляют примерно 10 км.