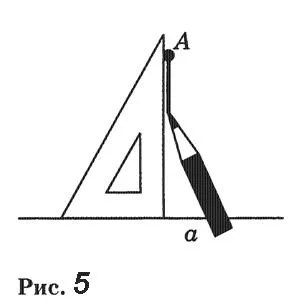
Давайте рассмотрим, как быстро нарисовать вертикальные линии. Самый простой способ сделать это — использовать линейку и карандаш на бумаге для флипчарта. Нарисуйте линии на флипчарте и пересеките их под углом 90°.
Как построить перпендикулярную прямую
Тема курса. Вертикальные линейные структуры.
- Познакомить учащихся с определением перпендикулярных прямых и их свойствах;
- Формирование умений анализировать изученный материал и навыков применения его для решения задач;
- Показать значимость изучаемых понятий;
- Развитие познавательной активности и самостоятельности получения знаний;
- Воспитание интереса к предмету, чувства прекрасного.
Интеграционные проверки того, чему они научились.
- Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными прямыми.
- Сумма смежных сторон равна 180?.
- Если два угла равны, то совместные с ними углы равны.
- Если угол не развёрнутый, то его градусная мера больше 180?.
- Угол, смежный с прямым углом, есть прямой угол.
- Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.
- Вертикальные углы различны.
- Если прямые пересекаются, значит, они перпендикулярны.
- Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной который имеет одним из своих концов их общую точку.
- Биссектрисой угла называется отрезок, который проходит из вершины треугольника, проходит межу его лучами и делит угол пополам.
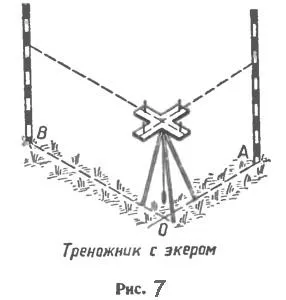
Вы много раз изучали геометрические узоры и рассматривали вертикальные линии. Например, смежные стороны прямоугольника перпендикулярны. Как можно убедиться, что две прямые линии перпендикулярны? В древние времена строители использовали гири, т.е. веревочные грузы, для контроля перпендикулярности стены к фундаменту дома. Отсюда и название «вертикальный»: латинское слово «perpendicular» означает «перпендикулярный». Чтобы провести вертикальную линию по прямой, просто нарисуйте прямой угол. Знаете ли вы, как чертить треугольники и как это делать с помощью угловой шлифовальной машины?
Теперь давайте выясним, какие линии называются перпендикулярными.
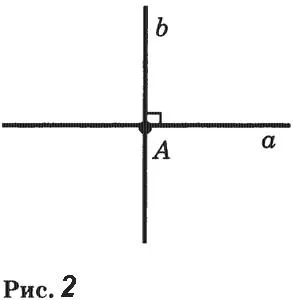
Две линии, пересекающиеся под прямым углом, называются перпендикулярными. (рис. 2)
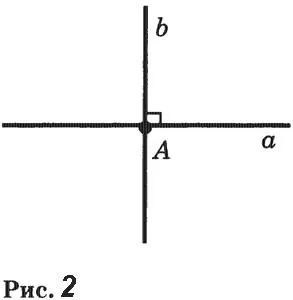
Перпендикулярная прямая может пересекать только одну произвольную точку на прямой.
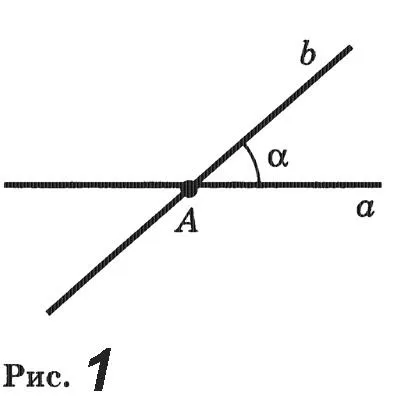
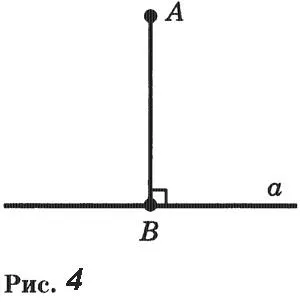
Пусть α — заданная прямая, а Α — точка на этой прямой. Одна полулиния линии а с начальной точкой А обозначается через ах (рис. 3). Определите по полулинии1 Угол (1b1), равный 90°. Тогда линия, содержащая b1перпендикулярна линии a.
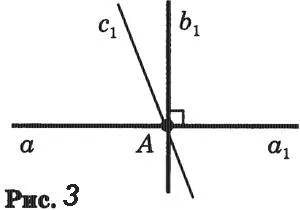
Как вы думаете, может ли отрезок быть перпендикулярным?
Да, потому что отрезок перпендикулярен прямой a. В общем случае две линии, лежащие на перпендикулярной прямой, можно назвать перпендикулярными. Какие другие геометрические фигуры можно сделать перпендикулярными? Варианты ответов: один радиус и один отрезок, два радиуса, один отрезок и одна прямая и т.д. Отрезки (или лучи) на вертикальной линии также называются вертикальными отрезками (или радиусами). Часто говорят, что вертикальные линии «перпендикулярны» друг другу. В математике слово «перпендикуляр» обозначается символом ┴. Если пересечение двух прямых перпендикулярно, то три других угла также перпендикулярны.
Таким образом, перпендикулярная линия — это две прямые линии, которые пересекаются и образуют четыре прямых угла. Далее вы узнаете, как создать перпендикулярную линию. Сначала постройте перпендикуляр, проходящий через точку, которая находится не на прямой, а на заданной прямой.
Давайте рассмотрим эти два случая более подробно.
Проведите вертикальную линию.
Проведите прямую, перпендикулярную данной прямой α, проходящую через точку Ο.
Возможны два варианта.
Давайте рассмотрим оба варианта по очереди.
Шаг 1. Постройте окружность произвольного радиуса r в центральной точке O. Окружность пересекает прямую в точках A и B.
Шаг 2. Постройте окружности радиуса AB из точек A и B. Пусть точка C будет точкой пересечения этих окружностей.
Обратите внимание, что в первом шаге вы получили точки A и B, построив окружность произвольного радиуса.
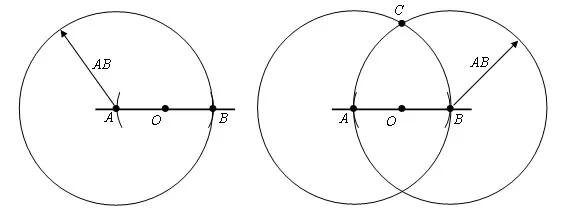
Шаг 3. Искомая прямая проходит через точки C и O.
Начертите секции AC и CB. ΔACO=ΔBCO из третьего символа в уравнении треугольника (AO = OB, AC = CB, CO — общий по построению). ∠COA = ∠COB = 90°. Прямая линия CO⊥AB.
Как и выше, все четыре угла, образованные пересечением двух прямых, перпендикулярны, если хотя бы один из них перпендикулярен, то есть равен 90° по прямой.
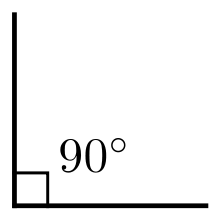
Второй вариант так же прост, но с немного другой отправной точкой для нахождения исходных точек A и B.
Шаг 1. Из точки O проведите окружность радиуса r так, чтобы она пересекала прямую α. Пусть A и B — точки пересечения окружности с линией a.
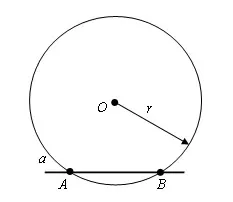
Шаг 2. Начертите окружность того же радиуса r с центрами в точках A и B. Пусть будет точка O.1 -пересечение этих окружностей. Она находится на другой полуплоскости, чем полуплоскость, на которой расположена точка O.
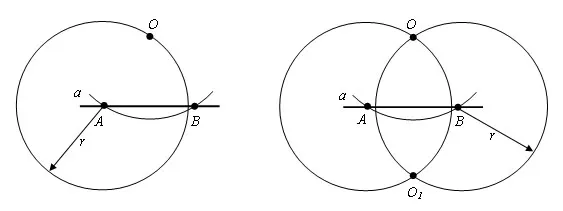
Шаг 3. Проведите прямую через точки O и O.1 в линию. Это та линия, которая нам нужна.
Оставьте линии OO1 и AB пересекаются в точке C. ΔAOB=ΔBO1A с третьим знаком тригонометрического тождества (AO = OB = AO1 = O1B, AB является общим по построению). Следовательно, ∠OAS = ∠O1AC. ΔOAC = ΔO1AC с первым знаком равенства треугольника (AO = AO1Из построения следует, что ∠OAS = ∠O1AC, AC — обычное явление). Следовательно, ∠OA = ∠O1CA, и если эти углы смежные, то они прямые. Следовательно, OC — перпендикуляр, опускающийся из точки O на прямую a.
Поэтому, используя компас и линейку, можно провести перпендикулярную линию независимо от того, в какой точке она должна проходить — внутри отрезка или за его пределами. Оба варианта предполагают три шага, единственная проблема — правильно найти начальные точки A и B.
Доказательство. Предположим, что a — заданная прямая, а A — ее точка. Одна из полупрямых линии a изображена в начальной точке A (рис. 3). Установите угол (α1β1) от полулинии (α1β1) на 90°. Тогда прямая, содержащая b1, перпендикулярна прямой a.
Определение перпендикулярных прямых, их свойства, характеристика
В геометрии параллельные и перпендикулярные линии имеют разное значение. Последняя является особым видом пересечения простейших геометрических фигур. Рассмотрим, какие линии называются перпендикулярными. После теоретического обзора мы покажем вам, как правильно рисовать такие конструкции с помощью угловых элементов. Вы также поймете, что такое перпендикуляр к прямой линии, его свойства и символику.
Рассмотрим пару прямых (a, b) или отрезков прямых (AB, CD), пересекающихся в точке O. В результате получается четыре угла. Если одна из них прямая, то другая также равна 90°. Сечения обозначаются ⟂:AB⟂CD. Точка O является общей для обеих геометрий, т.е. точкой их пересечения.
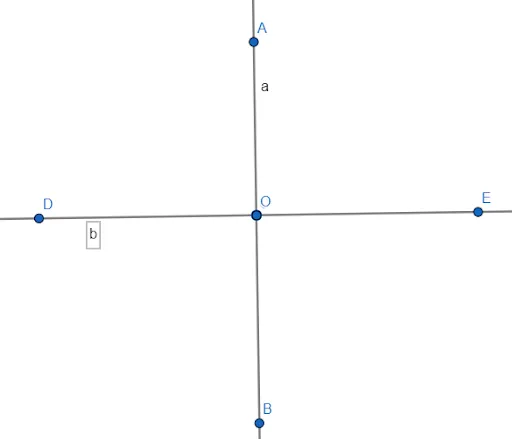
Теперь мы знаем, что такое перпендикулярная линия. Дана прямая α(ΑΒ) и точка Γ, не лежащая на ней. Если отрезок CD образует прямой угол с AB, то соединяющий их отрезок CD называется перпендикуляром. Точка D является основанием перпендикулярной линии.
Способы построения
Давайте рассмотрим, как быстро нарисовать вертикальные линии. Самый простой способ сделать это — использовать линейку и карандаш на бумаге для флипчарта. Нарисуйте линии на флипчарте и пересеките их под углом 90°.
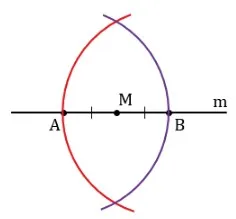
Второй метод является более сложным. Дана прямая m с точкой m: m ∈ m. Постройте отрезок прямой PQ, проходящий через m и пересекающий m под прямым углом.
- Произвольно чертится линия (желательно горизонтально) m, на неё наносится точка M в произвольном месте.
- Игла циркуля устанавливается в точку M, на лучах m ставится пара засечек на одинаковом расстоянии от M: это отрезки AM и MB, равные по длине.
- Игла циркуля устанавливается последовательно в точки A и B, строятся дуги, приблизительно заканчивающиеся в точках, из которых к M будет опускаться перпендикуляр. Важно, чтобы части окружности пересеклись под и над m в точках P, Q.
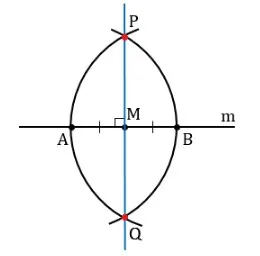
Теперь посмотрим, как доказать, что отрезок (отрезок прямой) перпендикулярен. Для этого рассмотрим треугольник APB или AQB (так как условия задачи одинаковы).
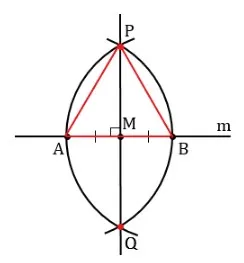
Поскольку обе стороны основного многоугольника состоят из равных радиусов окружностей, их длины равны: получается равнобедренный треугольник с AP=PB. Из условий задачи следует, что ΑΜ=ΒΜ, поэтому MP — медиана равнобедренного треугольника (исходя из определения этого понятия). PM — высота геометрической фигуры и перпендикулярна основанию: PM⟂AB, что и требовалось доказать.
Постройте прямую m и точку M не на ней. Постройте окружность с парами точек A и B, центр которой M пересекает m.
Начертите окружность с центрами A и B, пересекающую M. Обозначим через N точки, симметричные относительно прямой M. Подключите их к секции MN.
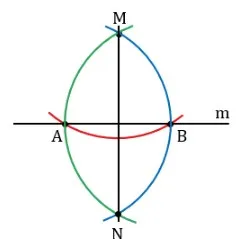
Докажите перпендикулярность MN к линии m.
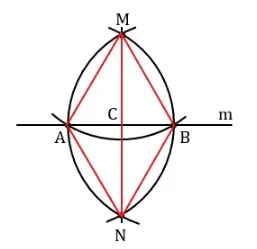
Задача
Докажите, что из точки можно провести только один перпендикуляр к отрезку прямой. Решение. Отметьте две свободные точки A и B на линии. Исходя из определения геометрии треугольника CAB, предположите, что хотя бы один из углов A или B является острым углом и предположите A. Для AB предположите, что угол EAB равен BAC. Отрезок длиной, равной AC, показан на линии AE. Соедините противоположную точку с секцией CE. CAD треугольника совпадает с EAD, на что указывает первый символ в эквивалентности треугольника. Поэтому углы EDA и CDA равны. В конце концов, они смежны и поэтому являются прямыми углами. Поэтому CE пересекает AB под углом 90°.
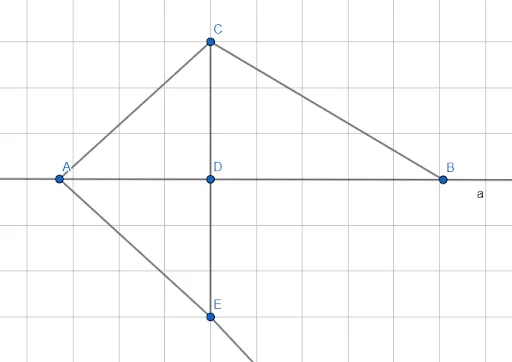
CE⟂a. Последний шаг: покажем, что мы можем провести только одну прямую, перпендикулярную из C в a. Предположение: можно провести второй перпендикуляр CD1 из C в a. Тогда уже существует △CDD1 с парой прямых углов, что невозможно. У треугольника может быть только один прямой угол. Следовательно, из точки c может падать только один перпендикуляр. Из рассматриваемого материала проследим логические свойства двух прямых a и b, перпендикулярных третьей c. a|||| b.
Перпендикулярное сечение — это сечение, пересекающееся под углом 90°.
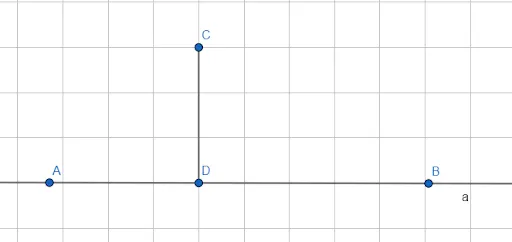
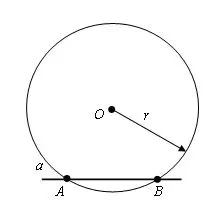
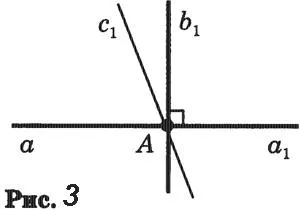
Перпендикуляр к данной прямой — это прямая, перпендикулярная данной прямой, один из концов которой является точкой пересечения. Этот конец линии называется основанием перпендикуляра. На рисунке 4 вертикаль AB проведена из точки A к прямой a. Точка B — основание вертикальной линии.
Циркуль и линейка
Другим простым способом вертикальный радиус можно разбить на участки. Для этого вам понадобятся простой карандаш, линейка и компас. Прямые углы могут быть образованы следующим образом.
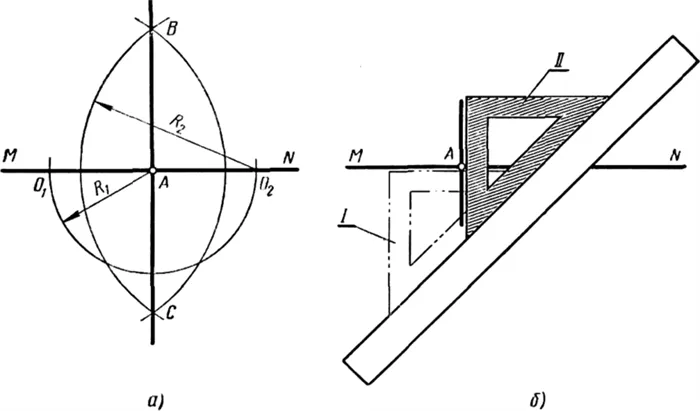
В результате должна получиться вертикальная линия, образующая с прямой линией угол 90°. Этот метод более сложный, чем первый метод. Это полезно, когда угол осадки отсутствует.
Теорема Пифагора
Знать только определение недостаточно, так как этот метод построения перпендикуляров требует теоремы Пифагора и ее доказательства. Наиболее распространенным вариантом является свойство египетского треугольника со сторонами 5, 4 и 3.
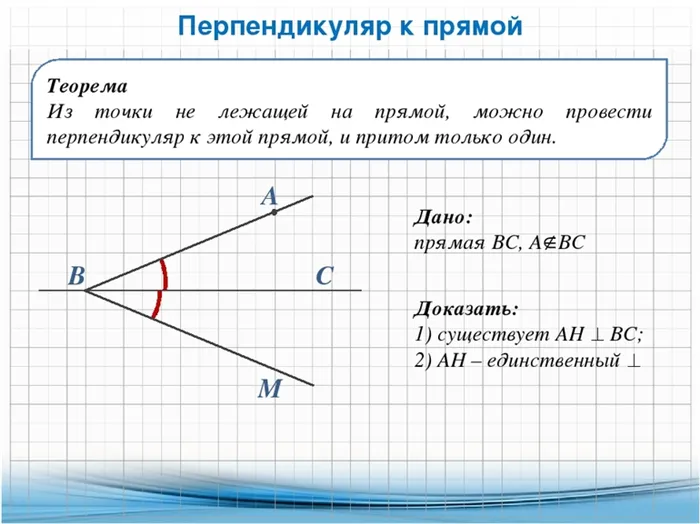
Из точки A измерьте и отметьте отрезок, равный 3. Результат — точка B. Далее необходимо нарисовать две одинаковые окружности. Первый центр находится в точке A, а второй — в точке B. Пересечение этих окружностей обозначено буквой C. Поэтому перпендикулярная линия — это линия, соединяющая две точки (A и C). Конечно, рекомендуется рассматривать это визуально на изображении или в виде рисунка.
Эта тема рассматривается в 7 классе геометрии. Учащиеся должны определить, что такое перпендикуляр к прямой линии. Затем линия проводится под углом 90° у своего основания.
Существует несколько способов оформления угла. В большинстве случаев для этого требуется компас. Чтобы нарисовать вертикальную линию, сделайте следующее
Построение перпендикулярной прямой
Затем попробуйте провести вертикальную линию с помощью компаса. Для этого у нас есть точка O и линия a.
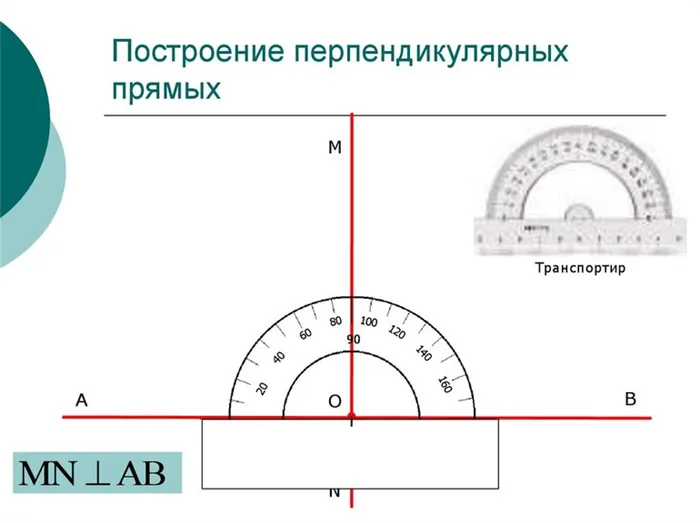
На первом рисунке линия проведена с точкой O, но на втором рисунке точка не находится на линии a.
Теперь давайте рассмотрим эти два варианта по отдельности.
1-й вариант
Сначала возьмите компас, поместите его в центр точки O и спроектируйте окружность произвольного радиуса. Теперь вы увидите, что эта окружность пересекает прямую A в двух точках. Пусть это будут точки A и B.
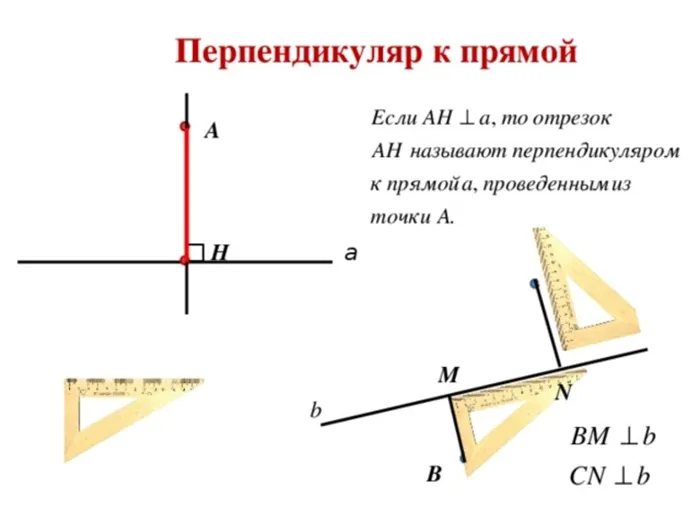
Затем нарисуйте окружности A и B. Радиус этих циклов будет AB, а точка C будет пересечением этих циклов. Возможно, вы помните, что изначально точки A и B были получены путем построения окружности с произвольным радиусом.
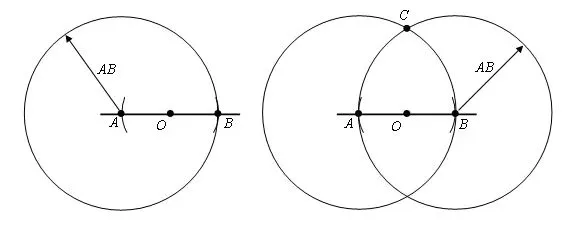
Наконец, вы увидите, что перпендикулярные линии проходят через C и O.
Для этого доказательства нам необходимо спроектировать секции AC и CB. Образовавшиеся треугольники равны: ΔACO=ΔBCO, что является третьим символом равенства треугольников, т.е. AO = OB, AC = CB, CO — общий от построения. Полученные углы am coa и am cob равны и оба имеют значение 90°. CO кажется перпендикулярной AB.
Отсюда можно сделать вывод, что угол, образованный при пересечении двух прямых, перпендикулярен, если хотя бы одна из них перпендикулярна. Другими словами, такой угол равен 90 градусам и является перпендикулярным.
2-й вариант
Теперь рассмотрим построение вертикальной прямой, когда заданная точка не лежит на прямой.
В этом случае с помощью компаса проведите окружность такого радиуса из точки, чтобы этот цикл пересекал прямую. Пусть a и b — пересечения этого цикла.
Затем постройте окружность того же радиуса, но с центрами в точках a и b. На диаграмме видно, что есть точка O1, которая является пересечением окружностей и находится на полууровне, но отличается от него. Это точка О.
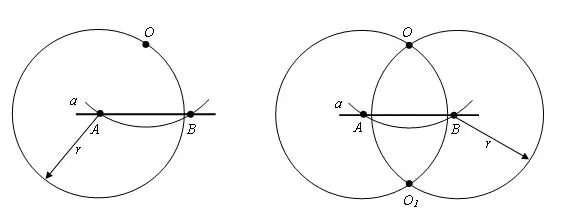
Далее мы проводим линию через O и O1. Это и есть искомая вертикальная линия.
Предположим, что точка пересечения прямых OO1 и ab находится в точке C. Предположим, что треугольники AOB и BO1A — равные треугольники и равны третьему знаку AO = AO1 = O1B. Углы OAC и O1AC кажутся равными. Треугольники OAC и O1AC равны AO1, следуя первой точке равенства треугольника AO, а из построения следует, что углы OAS и O1AC равны общему AC. Следовательно, угол OA равен углу O1CA, который является прямым, так как они конкретны. Поэтому делаем вывод, что OC — перпендикуляр, падающий из O на прямую A.
Рассмотрим пару прямых (a, b) или отрезков прямых (AB, CD), пересекающихся в точке O. В результате получается четыре угла. Если одна из них прямая, то другая также равна 90°. Сечения обозначаются ⟂:AB⟂CD. Точка O является общей для обеих геометрий, т.е. точкой их пересечения.
Перпендикулярные прямые
Этот урок напоминает учащимся о понятии прямых углов. Сформируйте представление о перпендикулярной линии. Ввести понятия перпендикулярных прямых и перпендикулярных отрезков (или лучей). Вы узнаете, как определить, что линия перпендикулярна. Вы также узнаете, как оформить вертикальную линию.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к другим видеосеминарам из этого набора, вам необходимо приобрести их из списка и добавить в свой личный гардероб.
Конспект урока «Перпендикулярные прямые»
Разобраться с этой темой нам поможет уже известный вам прямой угол . Напоминаем, что прямой угол – это угол, градусная мера которого равна
Две линии, образующие при пересечении прямой угол, называются перпендикулярами.

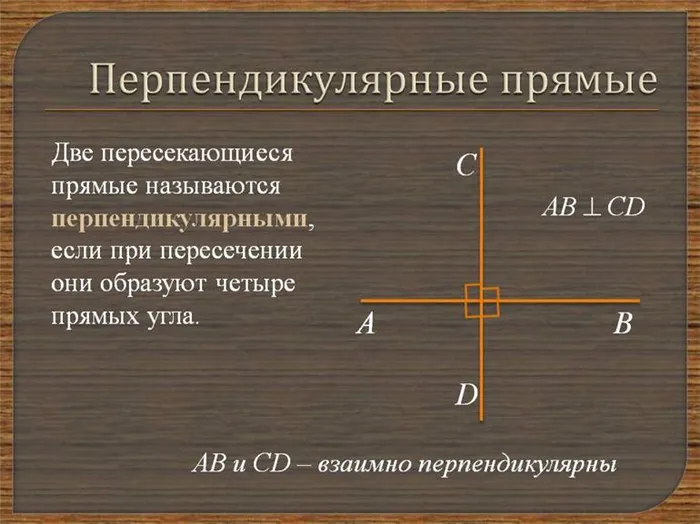
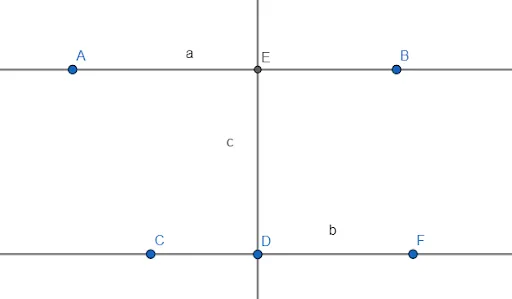
AB и C пересекаются, но не перпендикулярны.Они не перпендикулярныОни не перпендикулярны, потому что не образуют четыре прямых угла.
Однако AB и EF пересекаются и образуют четыре прямых угла.
Прямые AB и EF называются перпендикулярными.
В математике слово «вертикальное n» обозначается специальным символом.
В математике вертикальные линии встречались неоднократно.
Например, если продлить смежные (т.е. примыкающие) стороны прямоугольника, то полученная линия будет перпендикулярной.
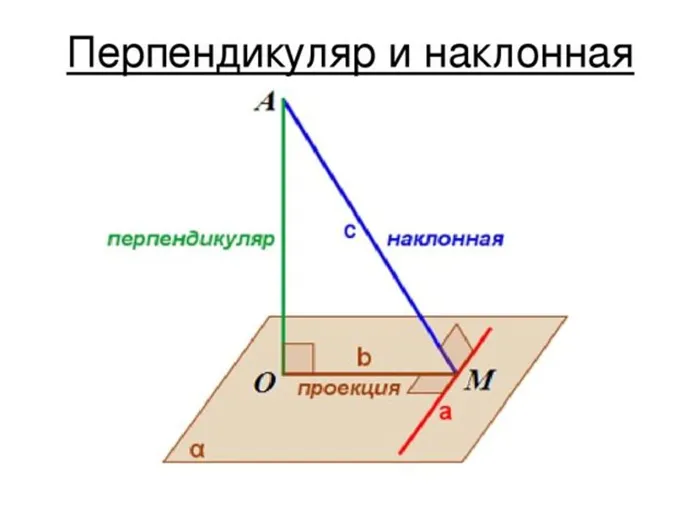
Видно, что две прямые линии перпендикулярны треугольникам и углам.
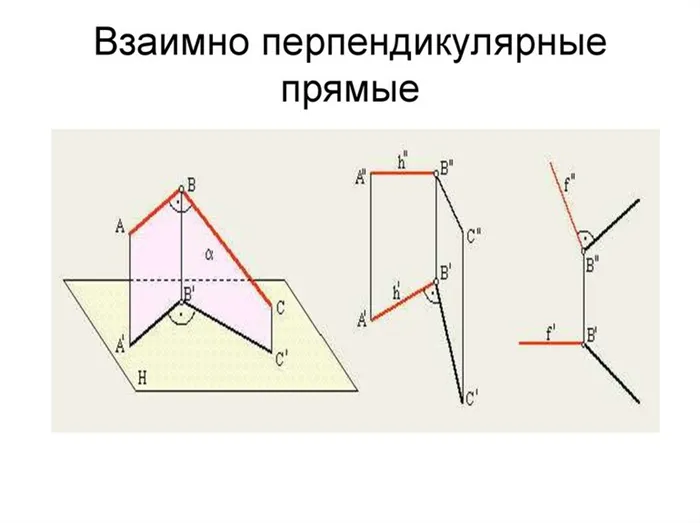
Кроме того, строитель может контролировать перпендикулярность стены к фундаменту дома с помощью тонкой, гибкой нити, т.е. грузом, о котором написал Боб.
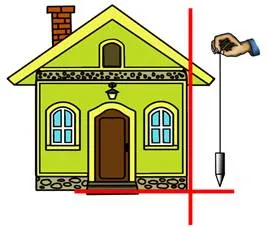
Кстати, латинское слово «вертикаль» означает «боб».
Нет необходимости измерять все четыре угла, чтобы убедиться, что две прямые линии перпендикулярны.
Если один угол правильный, то остальные три тоже правильные.
Например, AD пересекает O с BC.
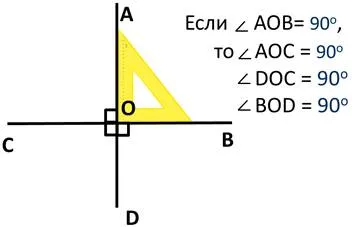
Тогда AOC, doc и bod также являются прямыми углами.
Рисовать перпендикулярные линии несложно.
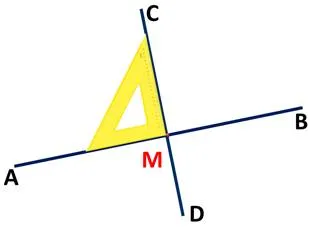
Например.Провести перпендикулярную прямую через точки этой прямой.:.
1) Проведите прямую AB, отметьте точку m на прямой и
2) Возьмите треугольник для построения, совместите прямоугольные стороны треугольника для построения с прямой AB и совместите вершину прямого угла треугольника для построения с точкой m.
3) Проведите линию вдоль второй стороны прямого угла чертежного треугольника.
Завершите построение двух перпендикулярных прямых, проходящих через точки на этой прямой.
Для построения вертикальной прямой, проходящей через точку, не лежащую на данной прямой, необходимо:.
1) Постройте любую прямую — отметьте точки, лежащие на прямой, точку








