В этом уроке мы познакомимся с понятиями «закрытая линия» и «открытая линия» и узнаем, как их различать и строить. Мы также рассмотрим такие понятия, как «звенья» и «вершины» кривой линии. Затем мы будем использовать эти знания для решения более сложных задач.
Точка и линия
Эти термины относятся к основным геометрическим объектам. Что может быть проще, чем объяснить, что такое точка и линия? Однако ученые из разных стран до сих пор не могут договориться об общих определениях.
Я не собираюсь рассказывать вам, что об этом говорят различные учебники, потому что вы здесь для того, чтобы понять и применить это, а не для того, чтобы пересказывать. Я объясню вам это так, чтобы это имело смысл.
Точка — это воображаемый геометрический объект, который не имеет размеров и ни из чего не состоит. Точка не имеет длины, ширины или высоты. Его невозможно измерить. Точка неделима. Он не состоит из других частей.
Что толку от него, если он воображаемый? Какова цель?
Точка имеет только одно назначение: указывать свое местоположение.
Пример: Точка на карте штурмана указывает на место назначения путешествия, т.е. его местонахождение.
Каждое ваше пожертвование увеличивает количество полезной и интересной информации на Easy-Math.ru!
Линия — это ряд точек, расположенных по порядку.
Например, представьте себе цепь. Вы можете представить, что каждое звено — это точка. Как цепь состоит из звеньев, соединенных друг с другом, так и линия, образно говоря, состоит из точек, соединенных друг с другом.
Рис. 1 Цепь и линия
Линия не имеет ширины или высоты, но ее длина может быть измерена. Линия состоит из точек.
Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Каково назначение линии?
Геометрическая точка действительно не имеет размеров, ее нельзя измерить. Но, как уже говорилось выше, он указывает на положение определенной вещи.

Давайте снова возьмем пример с моряком. Вы проехали на машине от своего дома до любимого кафе.
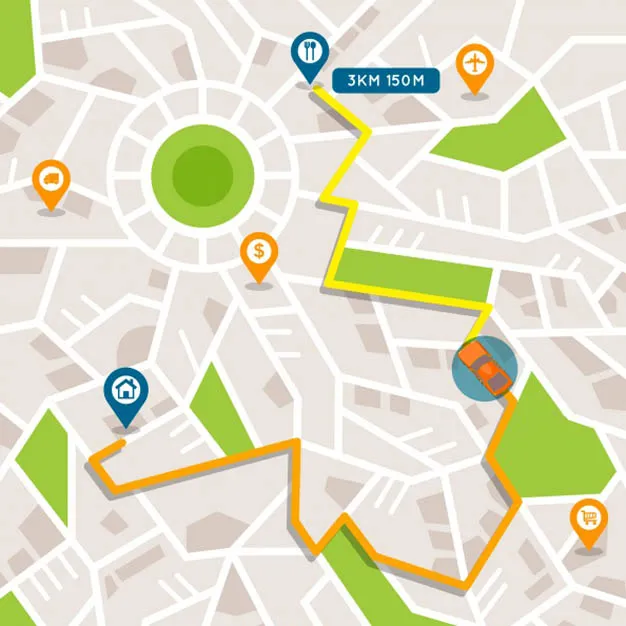
Рисунок 2 Траектория движения автомобиля
Можем ли мы представить автомобиль в виде точки? Да, мы можем. Во время поездки автомобиль менял свое положение. Чтобы показать на карте, где именно находился автомобиль во время своего путешествия, мы обозначим эти места точками. Чтобы упростить рисунок, мы можем заменить автомобиль точкой. Затем мы можем нарисовать весь маршрут от дома до кафе (набор мест, куда едет машина) в виде прямой, то есть проходящей через точки одну за другой. А поскольку путь от дома до кафе имеет определенную длину, нарисованная линия имеет длину, соответствующую этому расстоянию, и поэтому линию можно измерить.
Таким образом, мы можем использовать линию для представления пути объекта и определения длины этого пути.
Еще одна цель, для которой используется линия, — обозначить границы объекта или диапазона (интервала).
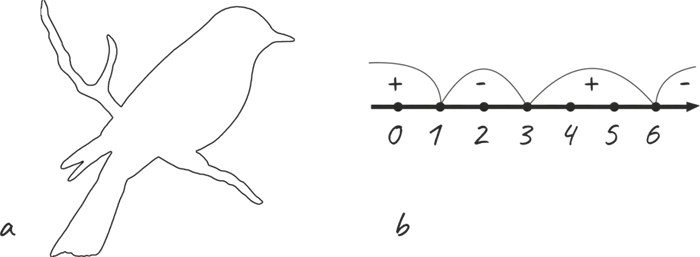
Рисунок 3 Контур и диапазон
На рисунке 3-a показан контур птицы на ветке с помощью линии, а на рисунке 3-b — пример решения неравенств методом интервалов.
Для чего нужна линия: 1. Она показывает путь объекта. 2. его можно использовать для измерения расстояния между определенными объектами. (3. Он может использоваться для обозначения границ объекта или фигуры. (4) Указывает на диапазон некоторых значений.
Обозначение точек и линий
Точка рисуется в виде маленького закрашенного круга. Чтобы было понятно, к какой точке она относится, она обозначается заглавными буквами латинского алфавита. Линии обозначаются строчными латинскими буквами.

Рисунок 4 Идентификация точек и линий
Взаимное расположение точек и линии
Точка может принадлежать или не принадлежать линии (т.е. быть одним из ее элементов).
Например, на рисунке 4.1 точки M и O принадлежат прямой c, а точки D, Z, F — нет.
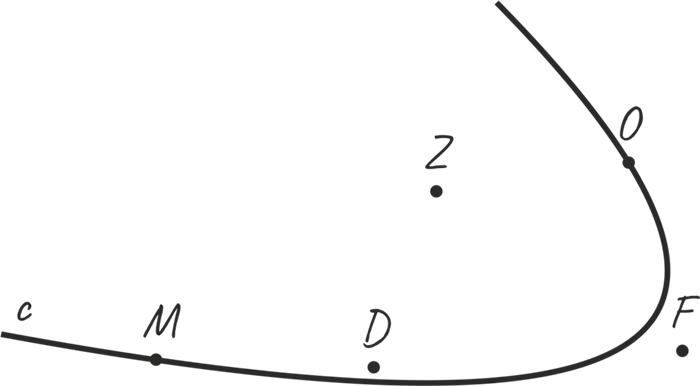
Рисунок 4.1 Расположение точек на прямой
В письменной форме точка обозначается символом в скобках с заглавной буквой латинского алфавита: (-) H
Чтобы указать, принадлежит ли точка прямой или нет, мы используем символ подстановки, который выглядит как перевернутая русская заглавная буква Е: ∈. Если точка не принадлежит прямой, то этот символ используется в перечеркнутом виде: ∉ .
Теперь я напишу то, что мы видели на рисунке 4.1, на языке геометрии, а вы попробуете прочитать это сами:
- (·) M ∈c
- (·)O ∈c
- (·)D ∉c
- (·)Z ∉c
- (·)F ∉c
Замкнутые самопересекающиеся ломаные
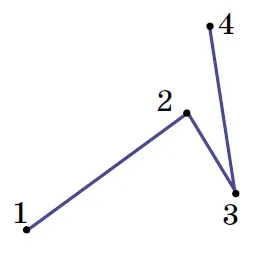
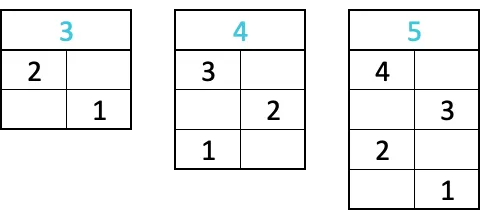
Эта статья о пунктирных линиях на плоскости. Для построения полилинии достаточно выбрать несколько точек (не менее трех), пронумеровать их в определенном порядке, а затем соединить точки последовательно соседними номерами в виде отрезков. Выбранные точки называются вершинами полилинии, а сегменты — звеньями (на рисунке 1 показана трехниточная полилиния с четырьмя вершинами).
Если хотя бы два звена полилинии пересекаются (в своих внутренних точках), она называется самопересекающейся (рис. 2 — самопересекающаяся полилиния из четырех звеньев).
Наконец, когда первая и последняя вершины полилинии совпадают, говорят, что полилиния замкнута. Количество вершин совпадает с количеством связей (на рисунке 3 показана замкнутая полилиния с пятью связями).
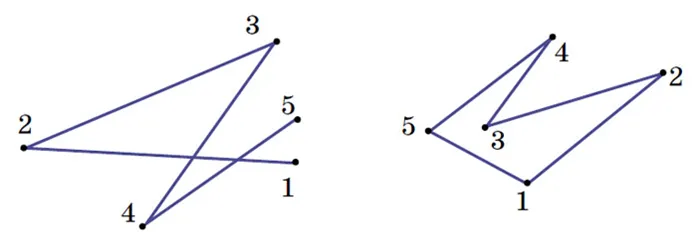
Рисунки 2 и 3
Нас интересуют замкнутые независимые многоугольники.
Начнем с задачи, предложенной А. Пешниным (его частные случаи были использованы в XXV турнире математических игр им.)
Задача 1
Сколько вершин может иметь замкнутая полилиния, которая пересекает каждую полилинию ровно дважды?
Очевидно, что замкнутая полилиния с тремя соединениями не может быть замкнутой сама по себе. Замкнутая полилиния с четырьмя вершинами также не удовлетворяет задаче, поскольку смежные звенья не могут пересекаться, и для каждого звена существует только одно несмежное звено. Хорошо известен пример пятизвенной полилинии — пятиконечная звезда (см. рисунок 4, а, где вершины полилинии делят круг на пять равных частей). Идея использования круга здесь не нужна, но она практична и пригодится позже.
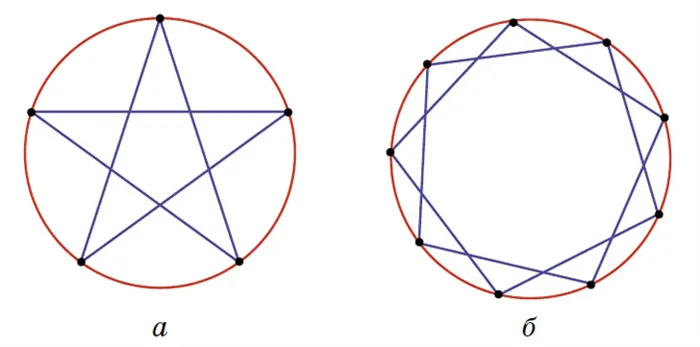

Этот пример показывает, что аналогичным образом можно построить любую полилинию, удовлетворяющую условию, с нечетным числом звеньев больше трех. Достаточно поместить в круг необходимое количество вершин и соединить их по одной. Рисунок 4, b, например, представляет собой желаемую полилинию с девятью звеньями.
Осталось только разобраться с многоугольниками с четным числом связей, начиная с шести.
Требуемой пунктирной линии из шести звеньев не существует, но мы можем доказать это, только перебрав все случаи, что не очень интересно.
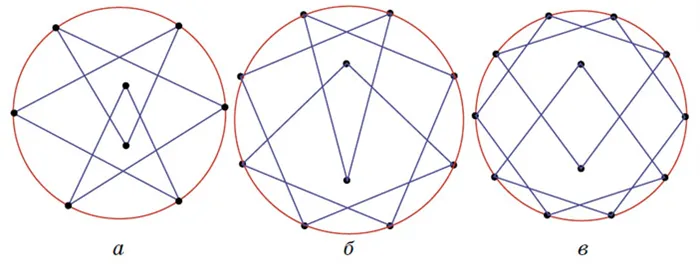
Есть хороший пример с восемью звеньями (рис. 5, а). Аналогично, можно построить полилинию, удовлетворяющую условию, с любым четным числом звеньев больше восьми. Как это делается, показано на примерах для десяти и двенадцати звеньев на рисунках 5, б и 5, в. Сначала отмечаем точки окружности, которые на две меньше, чем нужно, и соединяем их единицей. При четном количестве точек получаем два замкнутых многоугольника, соединения которых пересекают все остальные многоугольники в двух точках. Затем удалите одно соединение в каждой полилинии и соедините полилинию с одной, используя еще две вершины внутри круга.
Есть более простой способ. Воспользуйтесь тем, что любое четное число больше восьми можно представить в виде суммы двух нечетных слагаемых, каждое из которых не меньше пяти.
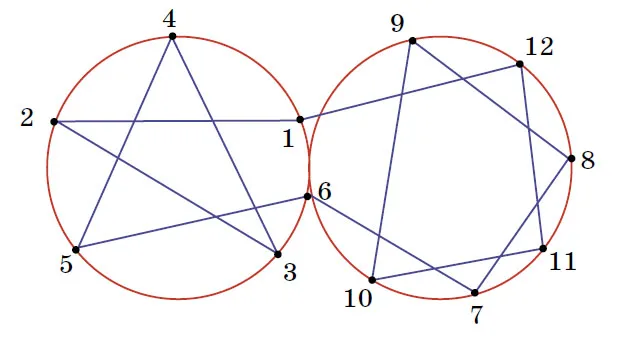
Например, покажем, как построить полилинию с двенадцатью звеньями, удовлетворяющую этому условию. Представим себе две окружности, касательные друг к другу в определенной точке. Построим пунктирную линию из пяти звеньев с одной стороны указанным способом и пунктирную линию из семи звеньев с другой стороны с точкой контакта в качестве общей вершины. Теперь эта точка «делится» (рис. 6, результатом деления являются вершины с номерами 1 и 6).
Аналогичным образом строятся все необходимые многоугольники с четным числом связей и более восьми.
Возникает вопрос: почему мы начали с двух пересечений связей, а не с одного, что кажется более естественным?
Дело в том, что такой порядок имеет больше смысла, потому что решение следующей проблемы в значительной степени основано на решении только что рассмотренной проблемы.
Задача 2
Сколько вершин может иметь замкнутая полилиния, которая пересекает каждое соединение ровно один раз?
Обратите внимание, что в этом случае звенья полилинии должны быть разбиты на непересекающиеся пары так, чтобы число звеньев полилинии было четным. Легко проверить, что замкнутая полилиния из четырех звеньев не удовлетворяет условию.
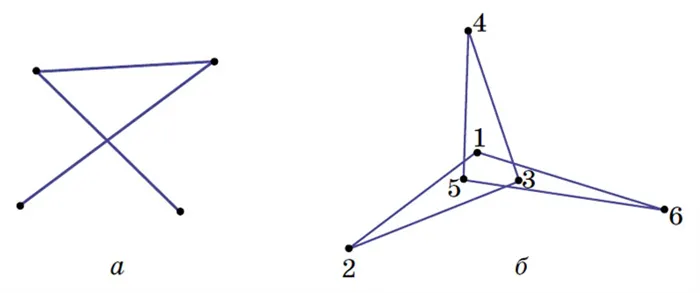
Пример шестизвенной полилинии может быть построен на основе следующего соображения: В дополнение к тому, что соседние звенья не могут пересекаться, звенья, проходящие через звено, не могут пересекаться. В этом случае образуется треугольник (рис. 7 a), в который можно только «войти», пересекая среднее звено, но не «выйти». Поэтому необходимо скрестить первое звено с четвертым, второе с пятым и третье с шестым (рис. 7, b).
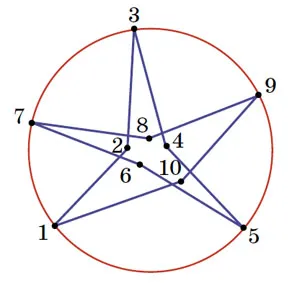
Читателю предлагается построить пример требуемой восьмизвенной пунктирной линии (см. задания в конце статьи). Однако пример десятизвенной линии можно получить, вернувшись к задаче 1. Рассмотрим пример замкнутой полилинии с пятью звеньями, которая пересекает каждое звено дважды (рис. 4); если мы разорвем каждое звено между двумя пересечениями, то получим желаемый пример (рис. 8). Аналогично, если мы рассмотрим семизвенную полилинию из задачи 1, мы получим решение для четырнадцатизвенной полилинии; пример восьмизвенной полилинии из задачи 1 поможет получить решение для шестнадцатизвенной полилинии, и так далее.
Этот метод подходит не только для построения двенадцатизвенной полилинии, поскольку не существует шестизвенной полилинии, в которой каждое звено пересекалось бы дважды. Но в этом случае мы можем использовать другую идею для решения проблемы 1: «расщепление». Постройте два многоугольника из рис. b с общей вершиной и «разветвите» их (рис. 9, результат разветвления — вершины под номерами 6 и 12). Понятно, что идея «ветвящихся» вершин более универсальна. Это также связано с тем, что можно комбинировать многоугольники с разным количеством соединений.
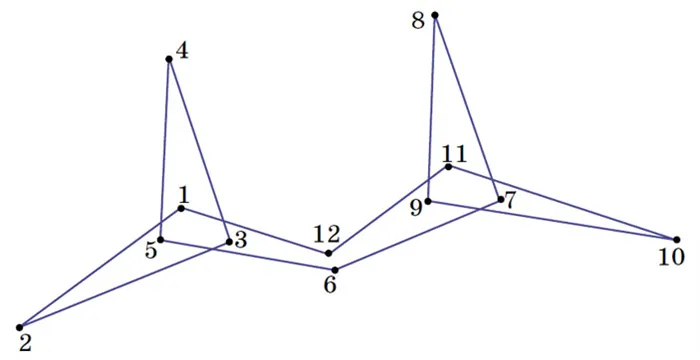
Есть надежда, что описанные выше идеи и методы могут помочь в решении других проблем.
Разновидности
В геометрии принято различать несколько типов структур:
- Замкнутые самопересекающиеся.
- Незамкнутые самопересекающиеся.
- Замкнутые без самопересечений.
- Незамкнутые без самопересечений.
Как описано выше, замкнутая, непересекающаяся фигура называется многоугольником.
Читайте также: Алканы: физические и химические свойства, применение.
Когда члены фигуры пересекаются друг с другом, фигура называется самопересекающейся.
Многоугольники
Многоугольник — это геометрическая фигура, характеризующаяся количеством углов и связей. Углы образуются парами звеньев замкнутой полилинии, которые сходятся в одной точке. Связи также называются сторонами многоугольника. Общие точки двух отрезков называются вершинами многоугольника.
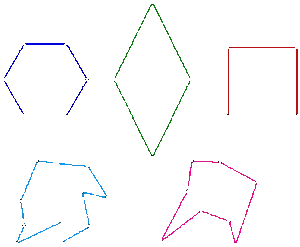
Количество звеньев или сторон в каждом многоугольнике равно количеству углов в том же многоугольнике. Замкнутая полилиния из трех отрезков называется треугольником, полилиния из четырех звеньев — четырехугольником. Фигура, состоящая из пяти сегментов, называется пятиугольником и так далее.
Часть плоскости, ограниченная замкнутой полилинией, называется плоским многоугольником. Другое его название — многоугольная плоскость.
Свойства
Ниже перечислены основные свойства, общие для всех многоугольников:
- Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
- Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
- Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
- Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости. Выиграть в российских казино может каждый. Вероятность получения выигрыша с азартных игр зависит только от удачливости игрока. Чтобы увеличить шансы на победу, стоит выбирать слоты с высоким уровнем RTP и различными бонусными опциями. Если же в слоте есть джекпот, шансы на крупный денежный приз увеличиваются в несколько раз.
- Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
- Если все стороны и углы многоугольника равны, он называется правильным.
Треугольники
В математике треугольник — это плоская геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой. Эти точки соединены тремя отрезками.
Точки представляют собой вершины треугольника, а отрезки — его стороны. Возле каждой вершины образуется угол треугольника. Таким образом, форма имеет три угла, что и дало ей название.
Различают следующие типы треугольников:
- Равносторонние — все стороны их равны по длине.
- Разносторонние — все стороны различаются по длине.
- Равнобедренные — две стороны из трех имеют одинаковую длину.
- Остроугольные — если все углы острые.
- Прямоугольные — если имеется прямой угол.
- Тупоугольные — если есть один тупой угол.
Четырехугольники
Плоская геометрическая фигура с четырьмя углами и четырьмя сторонами называется четырехугольником.
Читайте также: Законы Ньютона простыми и короткими словами: формулировки и примеры
Если все углы четырехугольника прямые, то это правильный треугольник.
Правильный четырехугольник называется квадратом.
Существуют и другие типы четырехугольников — ромбы, трапеции, параллелограммы и т.д. Общие правила, описанные выше, применимы ко всем из них.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Ломаная линия
Полилиния состоит из сегментов.
Конец одного сегмента является началом другого. Никакие два соседних звена не лежат на одной линии.
Концы каждого звена являются вершинами. Они могут быть идентифицированы по буквам.
Полилиния может быть открытой полилинией.
Открытая полилиния может быть преобразована в закрытую полилинию.
Такая замкнутая полилиния называется треугольником.
Она имеет три вершины.
Треугольник состоит из трех звеньев.
Замкнутая полилиния с четырьмя звеньями называется четырехугольником.
Замкнутая полилиния с пятью или шестью звеньями называется многоугольником.
Чтобы найти длину полилинии, измерьте длину каждого звена и сложите их длины.
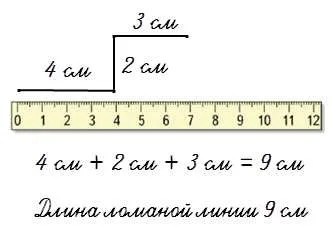
Поделитесь им с друзьями в социальных сетях:
Советуем посмотреть:
Точка. Кривая. Одна точка, одна кривая, одна линия.
Точка. Короче. Более узкий. Шире. Одинаковой длины и ширины.
Правило встречается в следующих упражнениях:
Страница 43, Моро, Волкова, Волкова, Степанова, Учебник, Часть 1.
Страница 71, Моро, Волкова, Степанова, Учебник, Часть 1.
Страница 101, Моро, Волкова, Степанова, Учебник, Часть 1
Страница 16, Моро, Волкова, Рабочая тетрадь, часть 1.
Страница 12. вариация 1. №3, Волкова, контрольные списки
Страница 5, Моро, Волк ова, Степанова, Школьный учебник, Часть 2.
Страница 25, Моро, Волкова, Волкова, Степанова, Учебник, Часть 2
Страница 41, Моро, Волкова, Степанова, школьный учебник, часть 2
Страница 60, Моро, Волкова, Степанова, Учебник, Часть 2
Страница 32, Моро, Волкова, Волкова, Рабочая тетрадь, Часть 2
страница 5, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, учебник, 1 часть
Страница 69, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, учебник, часть 1
Задача 31, Моро, Волкова, Волкова, Рабочая тетрадь, Часть 1.
Страница 20. вариант 1, часть 3, Моро, Волкова, рабочие тетради.
Страница 24. экзамен 1. вариант 1, Моро, Волкова, контрольные работы.
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 2.
Страница 82, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 2.
Страница 110, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 2.
Страница 51, Моро, Волкова, Волкова, Рабочая тетрадь, Часть 2
Страница 78, Моро, Волкова, Моро, Волкова, Рабочая тетрадь, Часть 2
страница 5, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, учебник, 1 часть
Страница 6, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 14, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 1
Страница 19, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 1
Страница 41, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 1
Страница 108, Моро, Волкова, Волкова, Степанова, Бантова, Бельтюкова, Учебник, Часть 1
Страница 5, Моро, Волкова, Волкова, Рабочая тетрадь, Часть 1
Страница 14, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 61, Моро, Волкова, рабочая тетрадь, 1 часть
Страница 6, Вариант 1, Часть 2, Моро, Волкова, Рабочая тетрадь, Часть 2.
Точка, линия, прямая, луч, отрезок, ломанная
— это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или латинской заглавной буквой. Разные точки обозначаются разными цифрами или буквами, чтобы их можно было различить.
Точка A, точка B, точка C
Точка 1, Точка 2, Точка 3
Можно нарисовать на листе бумаги три точки "А" и попросить ребенка провести линию через две точки "А". Но как узнать, какие именно? AAA
— это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается маленькими латинскими буквами (строчными)
Линия a, линия b, линия c
Линия может быть
- , если её начало и конец находятся в одной точке,
- , если её начало и конец не соединены
закрытые линии
открытые линии
Вы вышли из своей квартиры, купили хлеб в магазине и вернулись в свою квартиру. Какую линию вы получили? Правильно, закрытая линия. Вы вернулись в исходную точку. Вы вышли из квартиры, купили хлеб в магазине, вышли на лестничную площадку и поговорили с соседом. Какую линию вы взяли? Открытая линия. Вы не вернулись в исходную точку. Вы вышли из квартиры и купили хлеб в магазине. Какую линию вы получили? Открыто. Вы не вернулись в исходную точку.
закрытые линии
линии без самопересечения
прямые линии
пунктирные линии
изогнутые линии
— это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже если видна только небольшая часть прямой линии, предполагается, что она продолжается бесконечно в обоих направлениях.
Он обозначается строчной латинской буквой. Или двумя латинскими буквами верхнего регистра — точки на прямой линии
прямая линия a
прямая линия AB
Прямые линии могут быть
- , если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- , если пересекаются под прямым углом (90°).
- , если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
— это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
Начальной точкой светового луча на рисунке является солнце.
солнце
Эта точка делит прямую линию на две части — два луча A A
Луч обозначается латинской буквой в нижнем регистре. Или две заглавные буквы, первая из которых — начальная точка луча, а вторая — конечная точка луча
Лучи а
rays-AB
лучи совпадают, когда
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
— это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. — это расстояние между его начальной и конечной точками
Через точку может проходить любое количество прямых, включая прямые линии
через две точки можно провести неограниченное количество кривых, но только одну линию
кривые линии, проходящие через две точки
прямая линия AB
Ломтик «отрезается» от линии, а сегмент остается. Из приведенного выше примера видно, что длина — это кратчайшее расстояние между двумя точками. ✂ BA✂