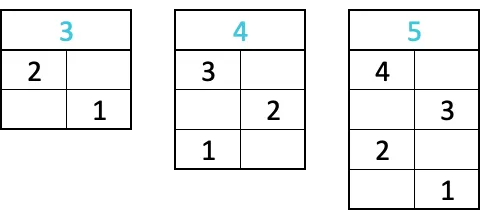
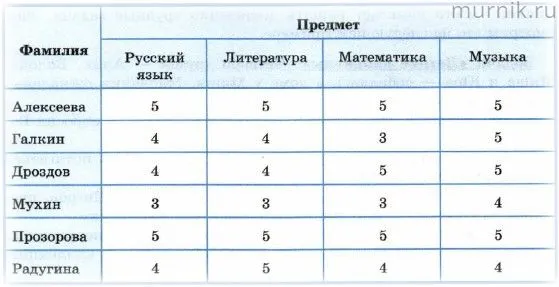
МНОГОГРАННИКИ (объемные геометрические фигуры): определения, формулы. Объемные геометрические фигуры и их названия.

Содержание

Четырехлетние дети сравнивают трехмерные и плоские фигуры, а дети постарше анализируют сложные иллюстрации, содержащие множество таких представлений. С 5 лет детей можно знакомить с геометрическими твердыми телами. С самого рождения дети узнают об окружающем мире, наблюдая за явлениями и предметами. Происходит визуальное и сенсорное обучение.

МНОГОГРАННИКИ (объемные геометрические фигуры): определения, формулы

Полиэдры (объемные геометрические фигуры): Определения, формулы для периметра и площади. Типы: Призма, параллелепипед (включая кубоид, куб), пирамида (включая усеченную пирамиду).

Призма — многогранник, у которого две грани — равные многоугольники ( основания ), лежащие в параллельных плоскостях, а остальные грани ( боковые ) — параллелограммы, имеющие общие стороны с этими многоугольниками.
Многоугольник, лежащий в основании, определяет название призмы : треугольник — треугольная призма, четырёхугольник — четырёхугольная призма; пятиугольник — пятиугольная призма (пентапризма) и т. д.
Прямая призма – призма, у которой боковые ребра перпендикулярны к плоскости основания (если нет – наклонная).
Правильна призма – призма, в основании которой лежит правильный многоугольник.
Высота призмы – перпендикуляр, опущенный из любой точки одного основания. на плоскость другого.

Типы для призм :

Объем призмы: V = S_o∙h Площадь: S = 2∙S_o+ S_{Страница}Где: V — объем призмы, S_o— площадь основания, h — высота, S_{Страница}— площадь всех сторон.

Параллелепипед

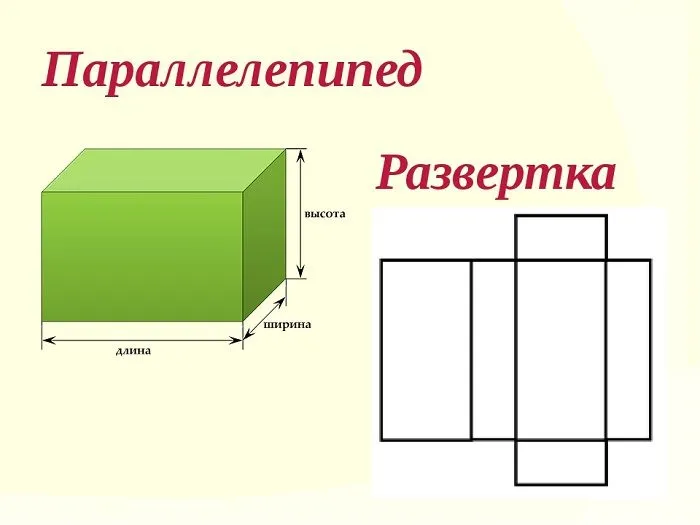
Параллелепипед — это призма, основанием которой является параллелограмм.

Параллелепипед имеет шесть граней и все они параллелограммы.
Противоположные грани попарно равны и параллельны.
Параллелепипед имеет четыре диагонали.
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Основанием параллелепипеда может быть любая грань.

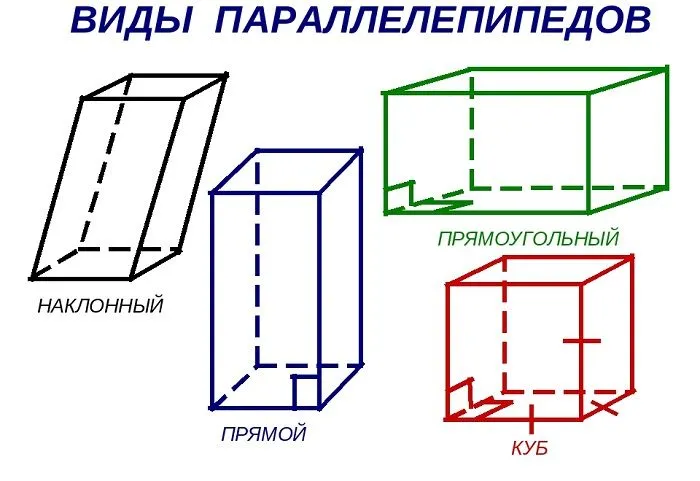
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Ромбоэдр — параллелепипед, грани которого являются равными ромбами.

Формулы для параллелепипеда :

Объем параллелепипеда: V = S_o∙h Площадь: S = 2∙S_o+ S_{Страница}Применяется следующее: V — объем параллелограмма, S_o— площадь основания, h — высота, S_{Страница}— площадь всех сторон.

Формулы для прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда: V = a∙b∙c = S_o∙ c Площадь прямоугольного параллелепипеда: S = 2-(S_a+S_b+S_c) или S = 2-(a-b+ b-c+ a-c) Диагональ: d =√(a 2 +b 2 +c 2 ) где: V — объем кубоида, a — длина, b — ширина, c — высота, So — площадь основания, S_a, S_b_,S_c— это площади соответствующих сторон.

Формулы для куба :

Объем куба: V = a 3 Площадь куба: S = 6-a 2 Диагональ: d = a√3 Где: V — объем куба, a — длина стороны куба.

Пирамида

Пирамида — многогранник, одна из граней которого ( основание ) — произвольный многоугольник, а остальные грани ( боковые ) — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
Вершина пирамиды – общая точка для всех треугольников.
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на ее основание.
Правильная пирамида – пирамида, у которой основание — правильный многоугольник, высота опускается в центр основания. В правильной пирамиде все боковые ребра равны, все боковые грани — равнобедренные треугольники. Высота треугольника боковой грани правильной пирамиды называется — апофема правильной пирамиды .
Правильная треугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный треугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники.

Формулы для правильной пирамиды :

Объем правильной пирамиды : V = 1/3 — (S_o— η) Площадь боковой поверхности правильной пирамиды: S_{Страница}= ½ — P_о— a Где: V — объем пирамиды, S_o— площадь основания пирамиды, S_{Страница}— площадь боковой поверхности, P_о— периметр основания пирамиды, h — высота пирамиды. a — абсцисса пирамиды.

Формулы для правильной треугольной пирамиды :

Объем правильной треугольной пирамиды: V = h-a 2 / (4/√3) Где: a — сторона правильного треугольника — основание правильной треугольной пирамиды, h — высота правильной треугольной пирамиды.

Формулы для правильной четырехугольной пирамиды :

Объем правильной четырехгранной пирамиды: V = 1/3 — h — a 2 Где: a — сторона квадрата — основание правильной четырехгранной пирамиды, h — высота правильной четырехгранной пирамиды.

Формулы для тетраэдра :

Объем тетраэдра: V = (√2 / 12) — a 3 Где V — объем тетраэдра, a — длина граней тетраэдра.

Педагогическая поддержка ребенка в образовательной среде

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курс «Инфоурок»).

В настоящее время 54 281 учреждение имеет право на накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.

Курсы повышения квалификации

Теория и методика педагогического проектирования

«Инструменты для формирования умений и навыков самостоятельной работы на уроках математики в 5-9 классах»

1 Слайд 3D геометрические фигуры

2 Слайд Геометрические твердые тела Геометрические твердые тела — это твердые тела, занимающие ненулевой объем в евклидовом (трехмерном) пространстве. Эти формы изучаются в разделе математики, известном как «пространственная геометрия». Знания о свойствах трехмерных форм используются в инженерном деле и науке. Рассмотрите вопрос в презентации «Геометрические трехмерные фигуры и их названия».

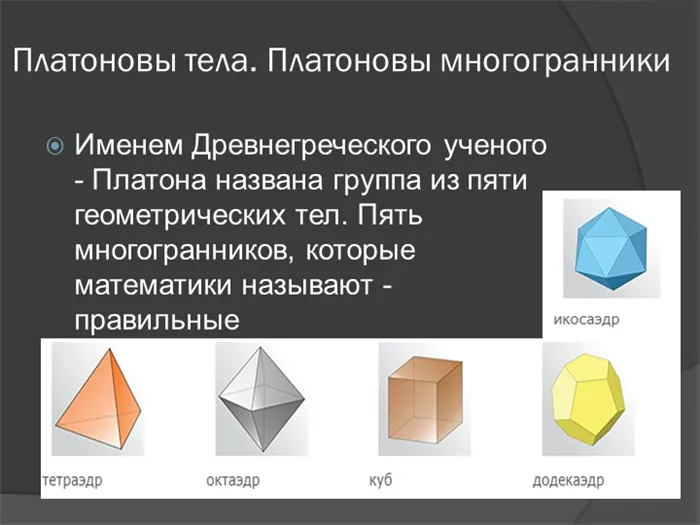
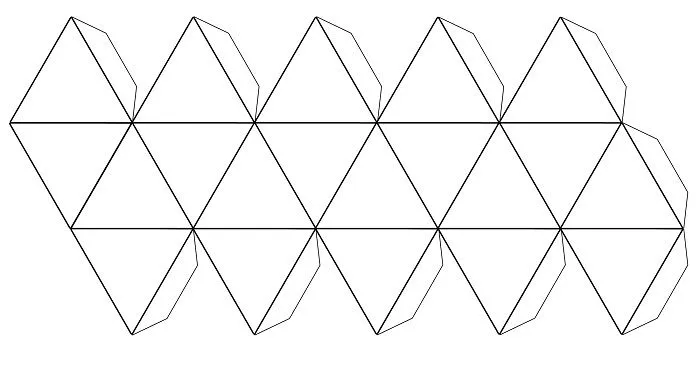
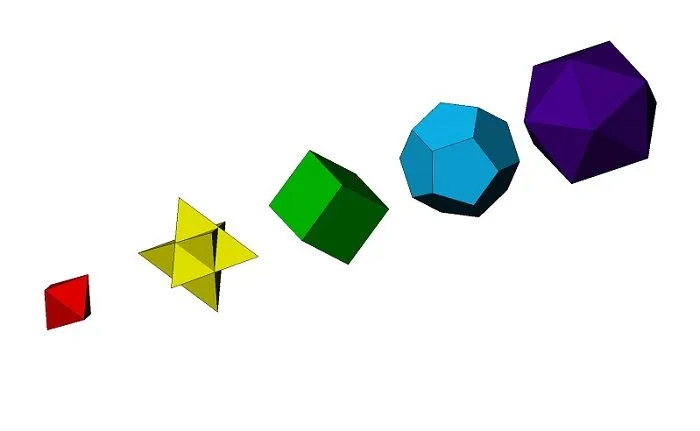
3 слайда Платоновы твердые тела. Многогранники Платона Группа из пяти геометрических твердых тел названа в честь древнегреческого ученого Платона. Пять многогранников, которые математики называют регулярными многогранниками.

4 слайд Какая связь с Платоном Древнегреческий ученый Платон не имел никакого отношения к открытию этих замечательных многогранников. Величайшим вкладом Платона было именно информирование людей о существовании таких объектов, как правильные многогранники. И если бы он просто рассказал их, большинство людей могли бы быстро забыть о них. Платон же наделял эти, казалось бы, простые предметы невероятной силой и мистическим значением, возводя их на вершину своего учения. Пытаясь объяснить природу всего сущего, Платон рассматривал пять правильных многогранников в качестве отправной точки для структуры каждого элемента: — огонь соответствовал тетраэдру; — воздух — октаэдру; — земля — гексаэдру; — вода — икосаэдру; — а додекаэдр соответствовал Вселенной.

Летописцы того времени подробно все записывали, и таким образом был создан целый научный трактат, как для современников Платона, так и для всех последующих поколений. Именно сила философии Платона и его мистических изречений захватила умы простых людей. А что будет дальше? И тогда люди уже неразрывно связали эти величины с идеями Платона. И в какой-то момент они говорят о пяти правильных многогранниках как о многогранниках Платона.

5 Слайд Геометрические тела из бисера Поскольку эти тела имеют конечные размеры в трех пространственных направлениях, геометрия использует для их описания трехосевую систему координат. Эти оси обладают следующими свойствами: они ортогональны друг другу, т.е. перпендикулярны друг другу. Эти оси нормализованы, т.е. базисные векторы каждой оси имеют одинаковую длину. Каждая из координатных осей является результатом векторного произведения двух других. Что касается геометрических объемных форм и их названий, то следует отметить, что все они относятся к одной из 2 основных категорий: категории многогранников. Эти формы имеют, в соответствии с названием категории, прямые края и плоские поверхности. Грань — это плоскость, ограничивающая фигуру. Соединение двух поверхностей называется ребром, соединение трех поверхностей — вершиной. К полиэдрам относятся геометрические формы кубов, тетраэдров, призм и пирамид. Для этих фигур применима теорема Эйлера, которая определяет соотношение между количеством граней (C), ребер (P) и вершин (B) каждого многогранника. Математически эта теорема может быть выражена следующим образом. Категория круглых твердых тел или твердых тел вращения. Эти элементы имеют по крайней мере одну изогнутую поверхность, которую они образуют. Например, сфера, конус, цилиндр, тор. Что касается свойств объемных элементов, то наиболее важными являются два из них: Наличие определенного объема, который фигура занимает в пространстве. Каждая трехмерная фигура имеет поверхность. Оба свойства описываются определенными математическими формулами для каждой фигуры. Ниже приведены простейшие геометрические трехмерные фигуры и их названия: Куб, пирамида, призма, тетраэдр и сфера.

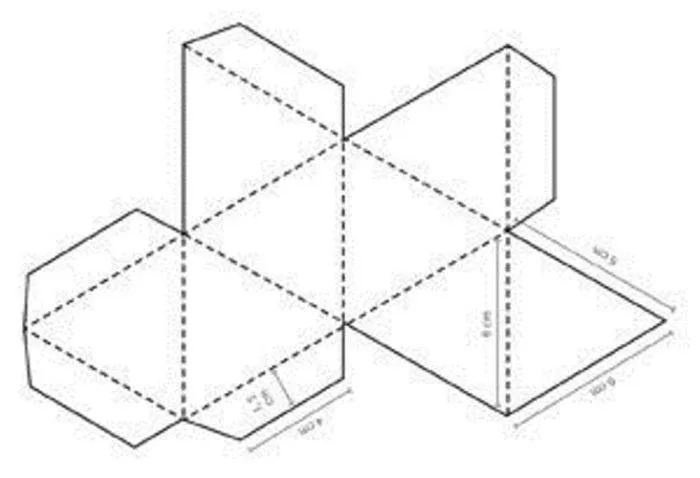
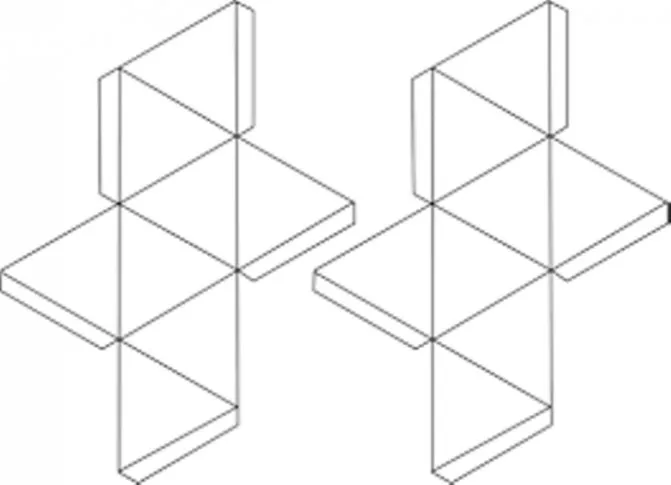
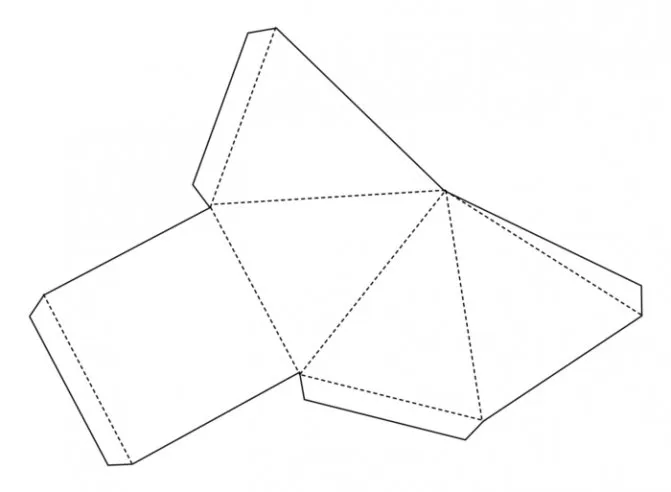
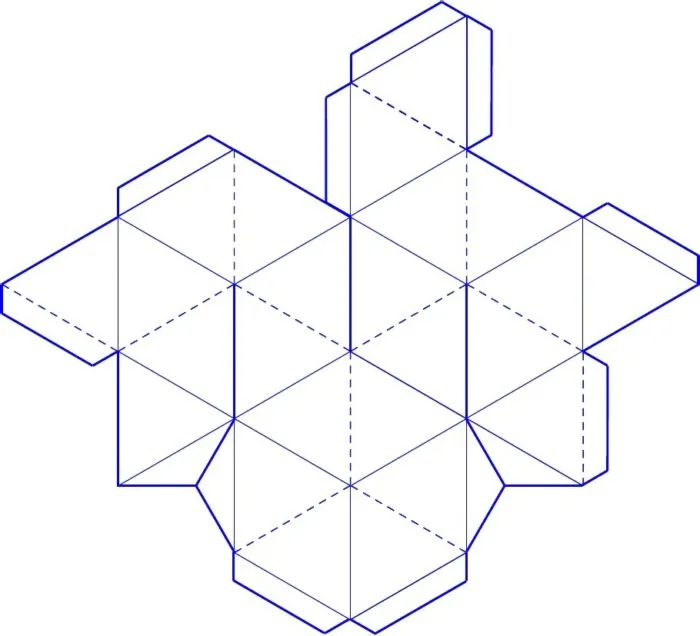
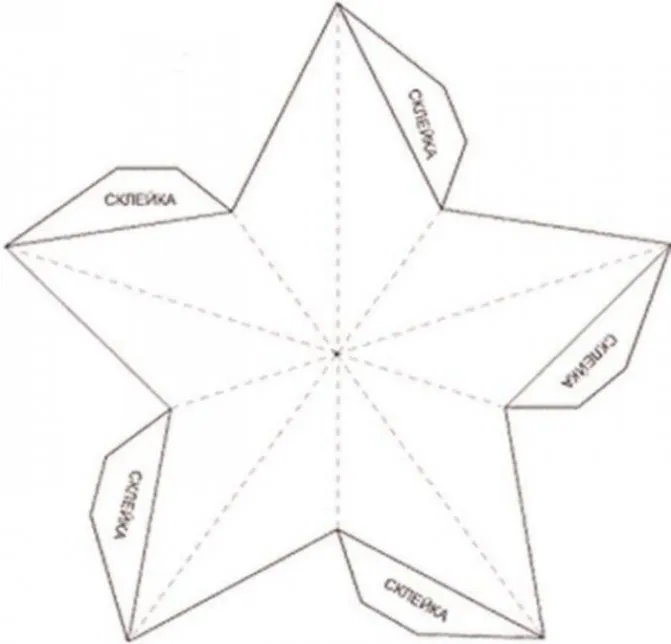
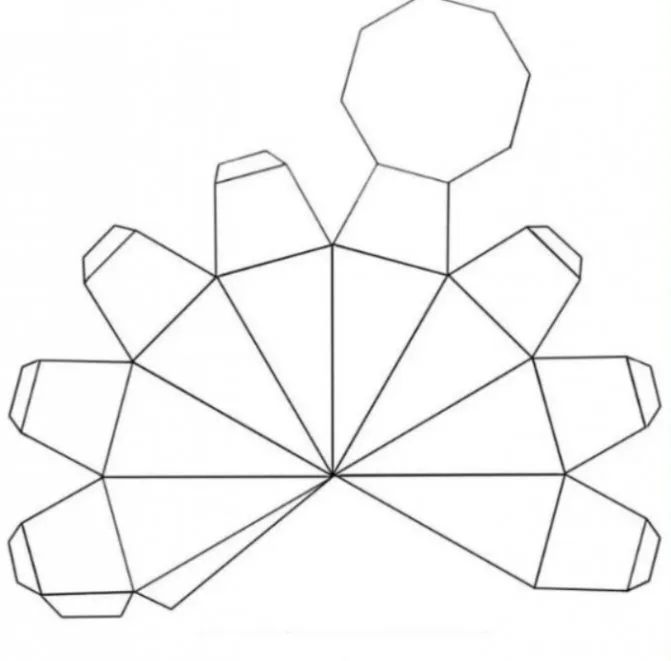
Пирамида — развертка. Развертка пирамиды для склеивания. Развертки из бумаги

Прямоугольник, квадрат, треугольник, трапеция и другие — геометрические фигуры из области точных наук. Пирамида — это многогранник. Основание этой фигуры — многоугольник, а боковые грани — треугольники с общей вершиной или трапеции. Модели изготавливаются для полного представления и изучения любого геометрического объекта. Для изготовления пирамиды используются различные материалы. Поверхность многогранной фигуры, развернутой на плоскости, называется разверткой. При создании макета помогает метод преобразования плоских объектов в объемные многогранники и некоторые знания геометрии. Нелегко сделать сверла из бумаги или картона. Вы должны уметь чертить планы в соответствии с заданными размерами.

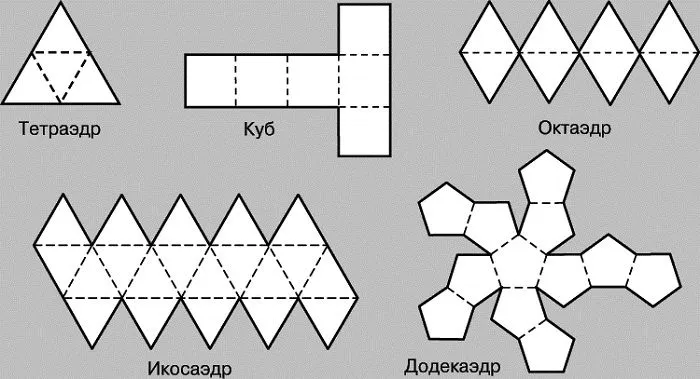
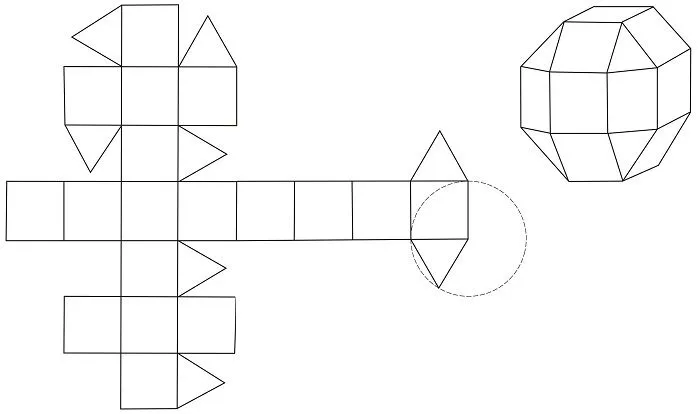
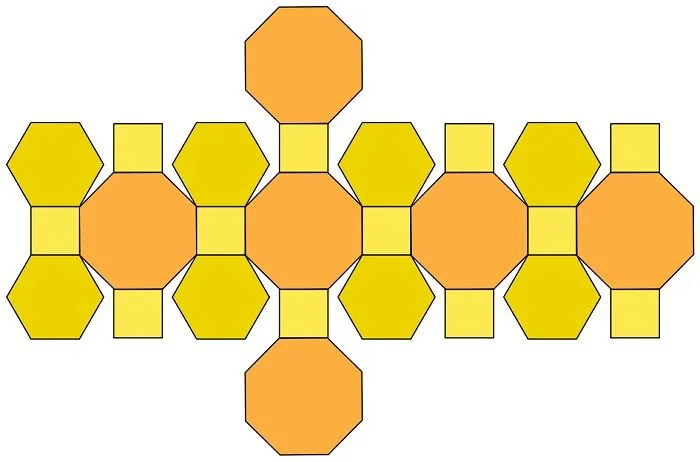
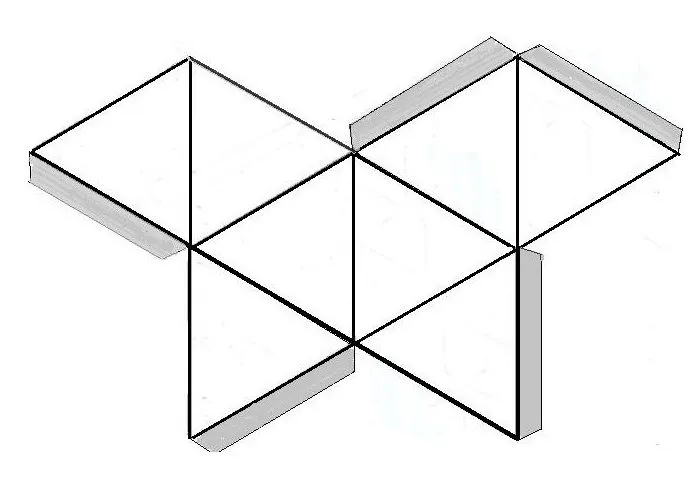
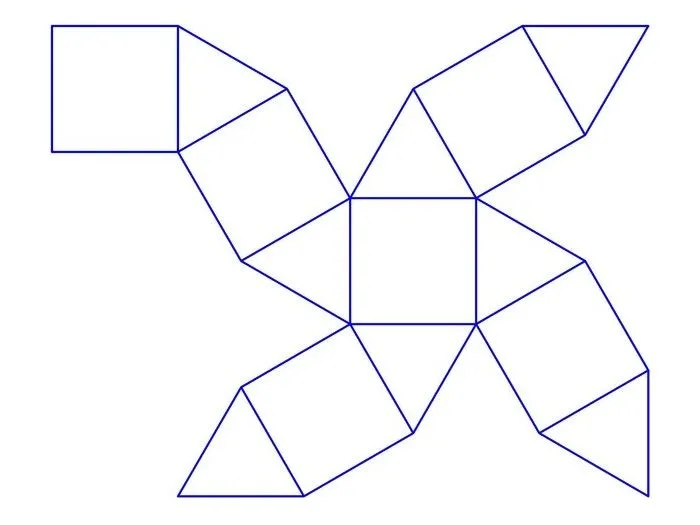
Схемы для вырезания

Учащиеся 1-2 классов знакомятся с простыми геометрическими фигурами и трехмерными фигурами в школе: Квадрат, куб, прямоугольник. Их несложно резать и клеить. Узоры развивают мелкую моторику детей и дают им первые представления о геометрии.

Учащиеся средних классов, работающие по шаблону, делают из бумаги сложные фигуры: шестиугольники, пятиугольники и цилиндры. Дети делают из бумаги кукольные домики, мебель, оригами, замок для маленьких игрушек, маски для лица (трехмерные называются многоугольными).

Конуса

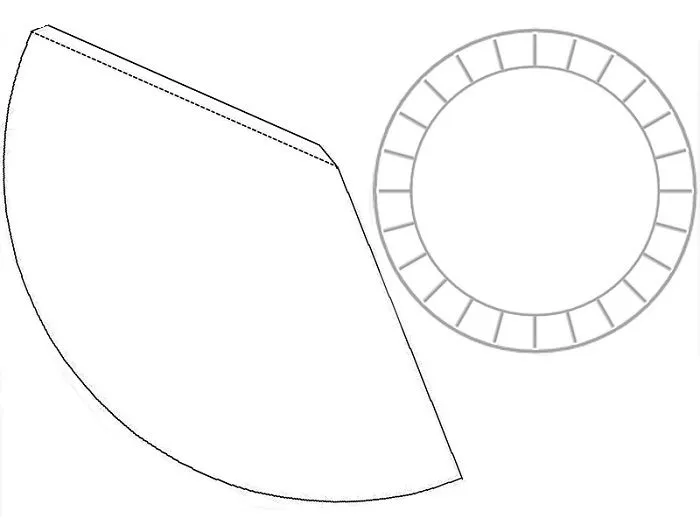
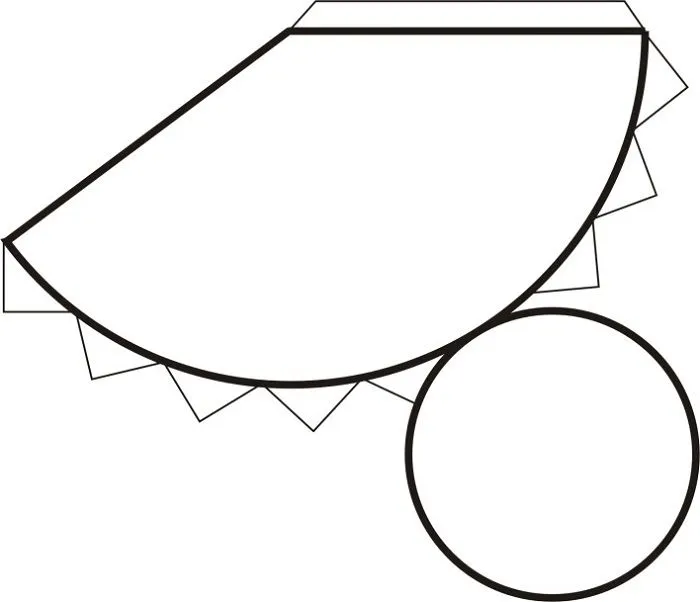
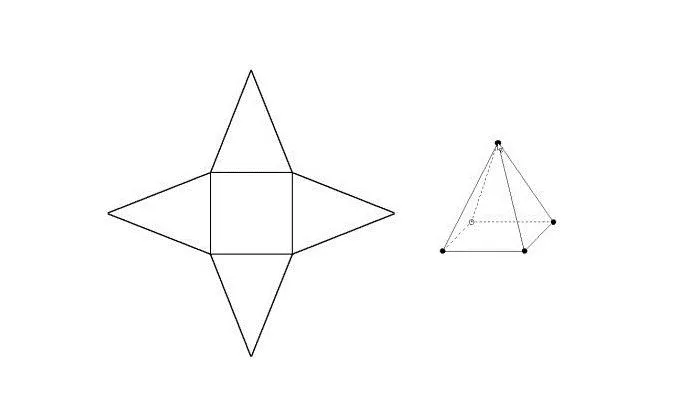
Пирамиды

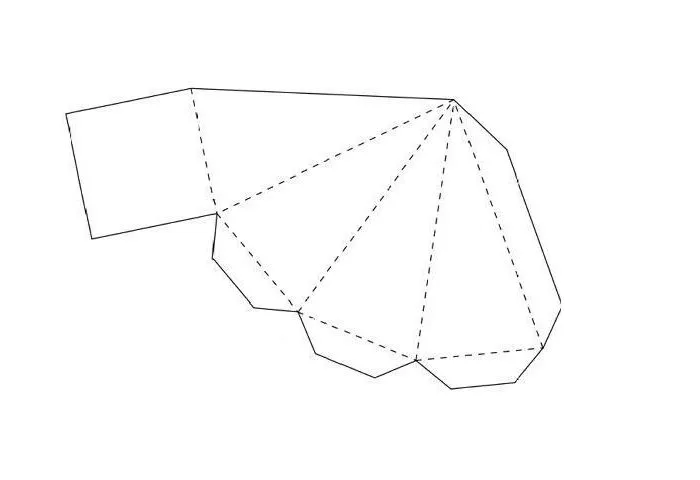
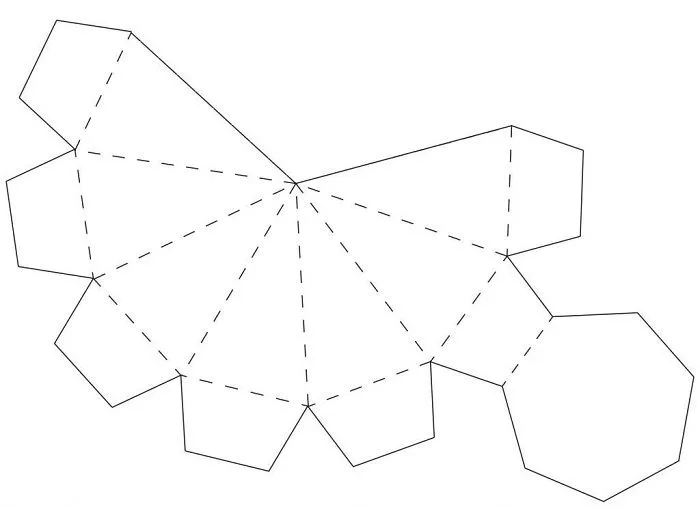
Шестигранника

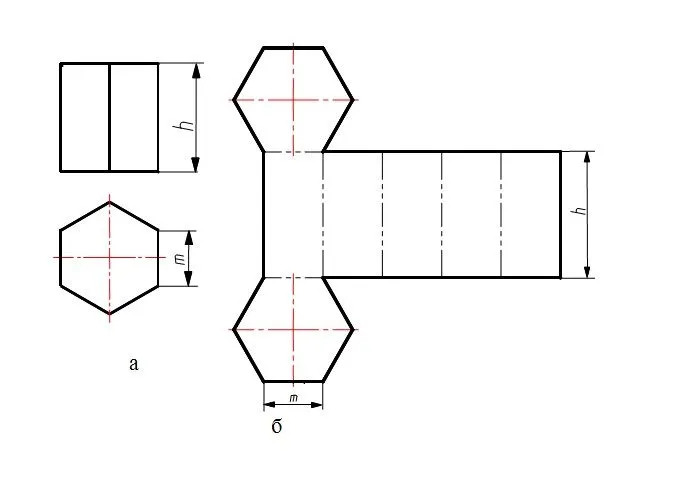
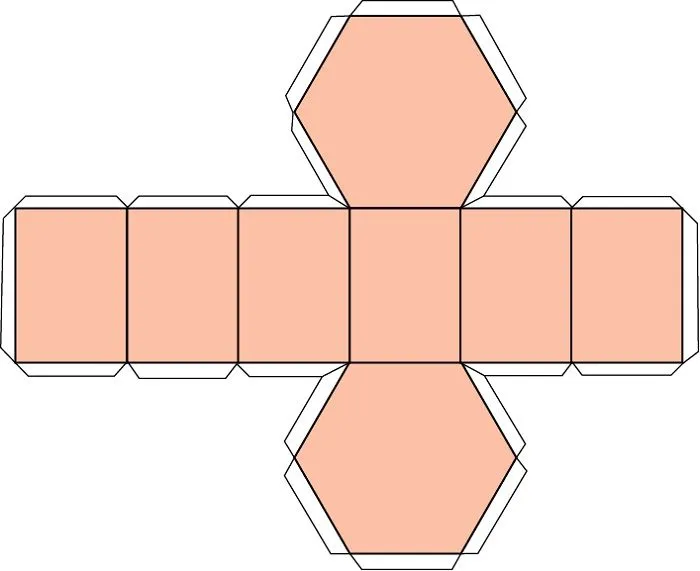
Макета с припусками

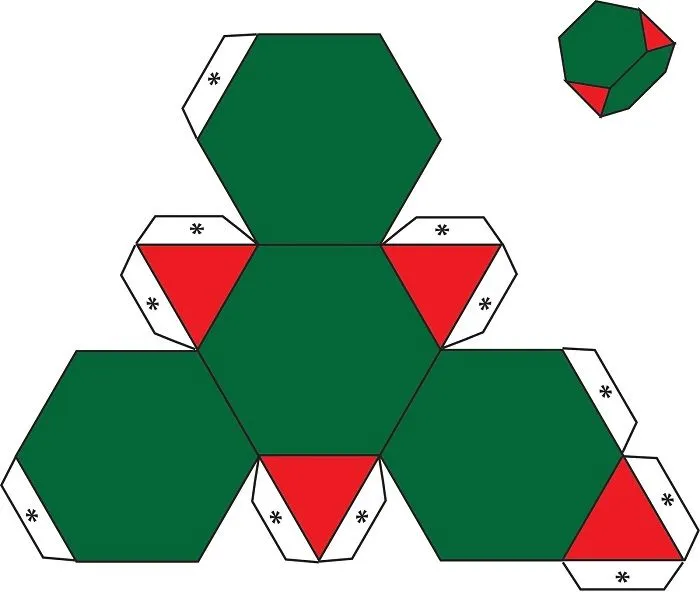
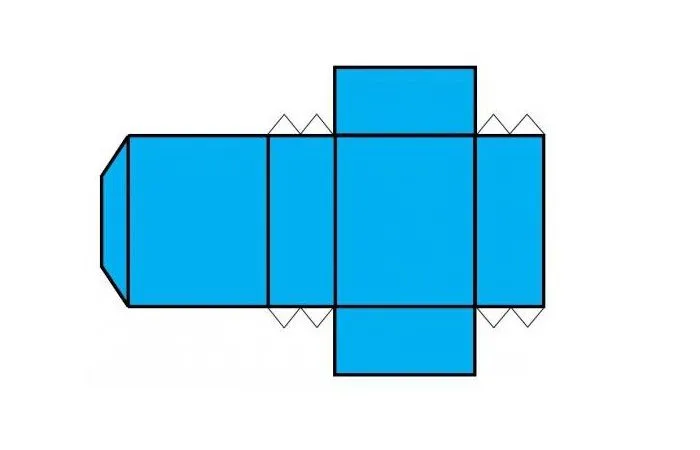
Параллелепипеда

Трапеции

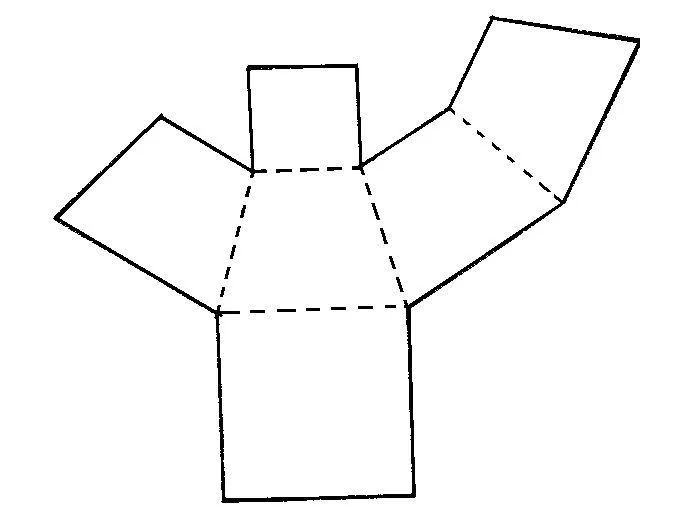
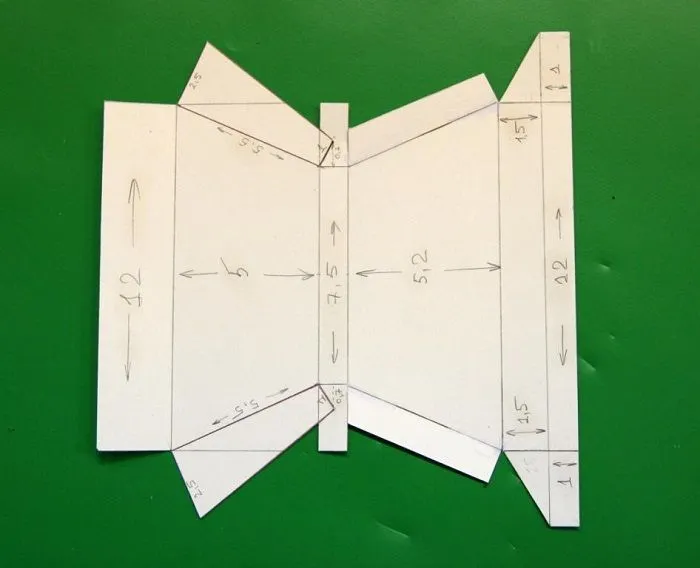
Овала

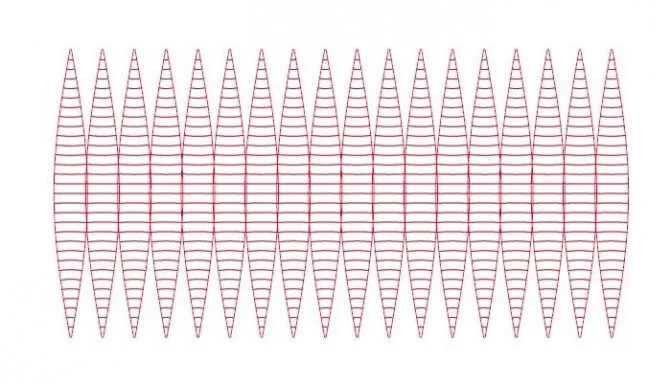
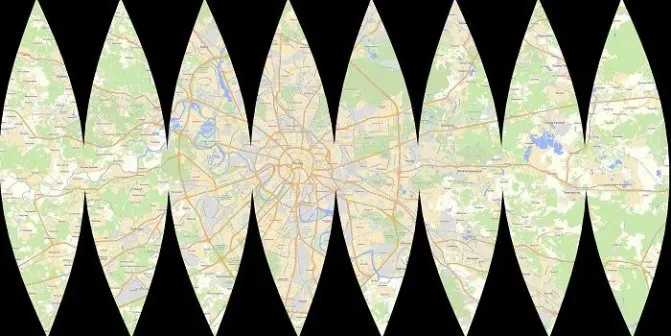
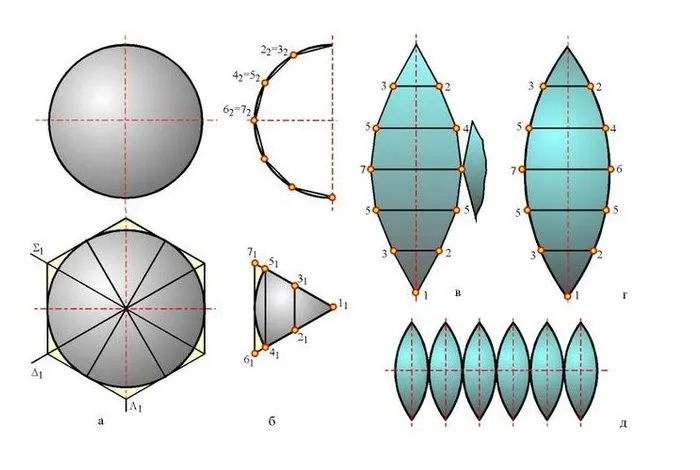
Узор из шаров состоит из 8, 12, 16 или более деталей. Существуют и другие способы изобразить мяч. Например, из 6 частей или 4 широких клиньев.

В качестве материала для изготовления плотного шара можно использовать картон или плотную бумагу.

Многогранника

Параллелограмма

Определение параметров

Сначала определите, как должна выглядеть пирамида. Форма пирамиды является основой для построения трехмерной фигуры. Выполнение проекта требует предельной точности. Если чертеж неправильный, геометрическую фигуру невозможно собрать. Предположим, вам нужно построить модель правильной треугольной пирамиды.

Каждое геометрическое тело обладает определенными свойствами. Основой этой фигуры является правильный многоугольник, вершина которого проецируется на его центр. Основание представляет собой равносторонний треугольник. Это условие определяет имя. Боковые грани пирамиды — это треугольники, количество которых зависит от многогранника, выбранного в качестве основания. В данном случае их будет три. Также важно знать размеры всех частей, из которых будет состоять пирамида. Бумажные рулоны изготавливаются в соответствии со всеми данными геометрической фигуры. Параметры будущей модели определяются заранее. Выбор материала зависит от этих данных.

Уроки начертательной геометрии для детей

Знакомство с начертательной геометрией формирует у детей пространственное мышление. Упражнения в такой сложной графической дисциплине должны быть понятными и максимально простыми.

При обучении первым основам геометрии до школы часто используются такие упражнения:

детям предоставляют плакаты с таблицами из квадратных ячеек, по которым необходимо определить и сравнить размер фигур;

глядя на наглядные материалы с изображением на них насекомых, составленных из различных фигур, ребенок должен рассказать, какие из них длиннее или короче;
разделение нарисованных форм на группы;
освоение связей между фигурами и числами при помощи подсчета форм и решения простых примеров;
рисование фигур на листах в клетку по предложенным параметрам;
освоение понятий больше-меньше, короче-длиннее путем применения бумажных полос с различной длиной для измерения цепочек с фигурами;
нахождение рисунков с присутствием в них геометрических фигур;
подсчет форм на предложенных изображениях;
рисование составных фигур из простых пар;
перечисление форм, которые есть в предлагаемых предметах;
ознакомление и запоминание фигур, нарисованных на плакатах;
обведение по трафаретам;
игры с изображениями различных форм;
нахождение лишних образцов среди одинаковых фигур;
сортировка форм по группам;
игры с конструктором или кубиками;
рисование мелками или на песке;

выкладывание в песочнице фигур из каштанов или желудей;
сравнение простых и объемных фигур с представленными примерами;
нахождение составных форм на плоских изображениях;
воспроизведение геометрических фигур с помощью лепки или рисования;
вырезание фигур и последующее их приклеивание к основе.
анализ изображения со сложными формами, опознание их составных деталей.

После того как дети полностью освоят все основные фигуры, рекомендуется постоянно повторять и декламировать их для лучшего закрепления и запоминания.

Дорисовывание плоской фигуры по образцу

Развивающие задания на рисование геометрических фигур способствуют их более быстрому запоминанию. В форме упражнения ребенок должен заполнить картинку карандашом и линейкой.

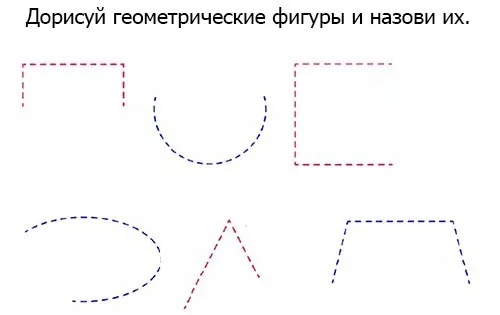
Во время выполнения упражнения:

Детям показывают фигуры и рассказывают о них. Далее приводят примеры похожих предметов, находящихся в помещении.
Распечатывают бланки с незаконченными фигурами. Контуры изображений должны быть пунктирными.
Произнести задание: обвести по точкам и завершить фигуры. Объяснить, чем является каждая из них.
Обсудить с детьми результат работы.

Частичная раскраска может быть завершена вместе с неполными фигурами. После завершения работы ребенка следует попросить дополнить картинку цветами.

Складывание геометрических фигур из пазлов

Чтобы лучше усвоить геометрические фигуры, детям предлагается собрать специальные пазлы. Вначале упражнения должны быть простыми, а затем постепенно усложняться. Благодаря этим заданиям развивается воображение, и дети учатся понимать, как расположены фигуры по отношению к плоскости.

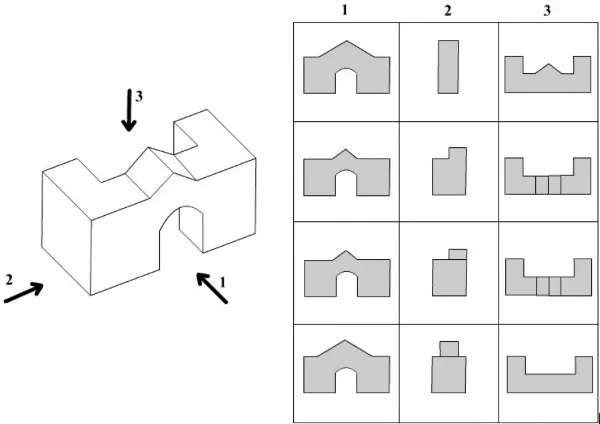
Пример упражнения с головоломкой:

Изготовить бланки с двумя рядами, в одном из которых изобразить простые фигуры, а во втором – сложные.
Предложить детям найти в нижних изображениях те, которые содержат в себе верхние.
Каждому ребенку объяснить получившийся результат.

Группировка простых фигур в сложные

Упражнение выполняется следующим образом:

Из картона вырезают напечатанные или нарисованные на нем простые фигуры.
Детям необходимо из предложенных заготовок сложить более сложные формы.
Для заучивания цифр можно просчитывать каждый вид фигур.

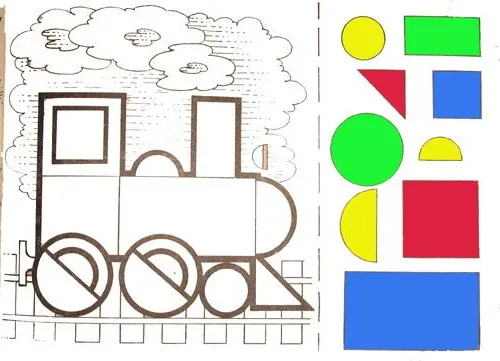
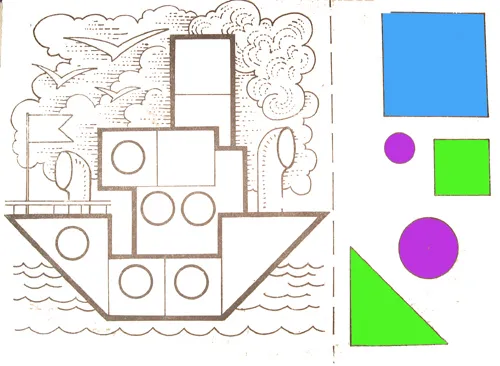
Чтобы усложнить задачу, детей просят сложить целые картинки из готовых шаблонов, например, самолет или животное.

Параллелограмм и ромб

Прямоугольник — это квадрат, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Противоположные стороны и углы равны.
Сумма любых двух соседних углов равна 180 градусам.
Диагонали пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит фигуру на два равных треугольника.

Общие формулы для вычисления площади фигур:

S = a × h, где a — сторона, h — высота.
S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a 2 × sinα.
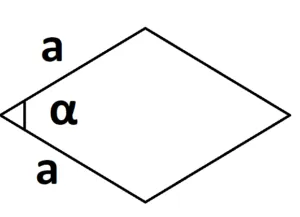
Для ромба: S = 0,5 × (d₁× d₂), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d₁× d₂) × sinβ, где β — угол между диагоналями.

Периметр ромба равен произведению длин сторон, умноженному на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — это сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, а b — высота.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

Прямоугольный. Один угол прямой, два других менее 90 градусов.
Остроугольный. Градус угла больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других острые.

В треугольнике против большего угла лежит большая сторона — и наоборот.
Сумма углов треугольника равна 180 градусов.
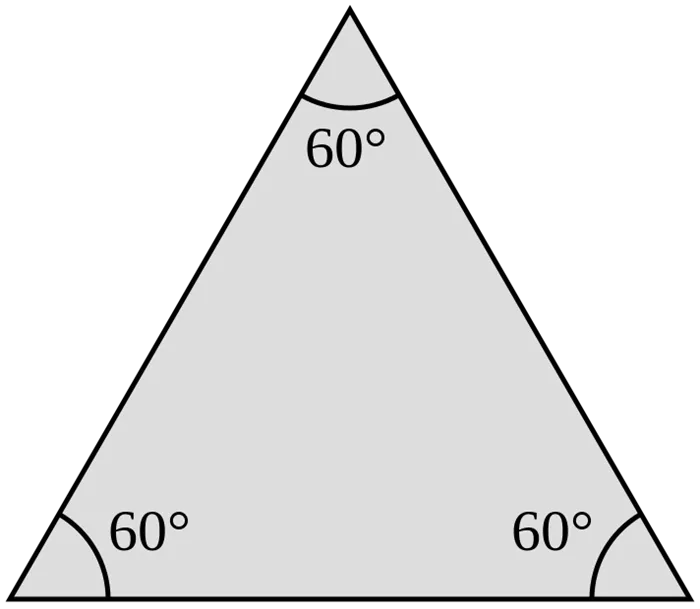
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Площадь треугольника можно вычислить несколькими способами на основе исходных данных, давайте рассмотрим их.

Если известна сторона и высота. S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.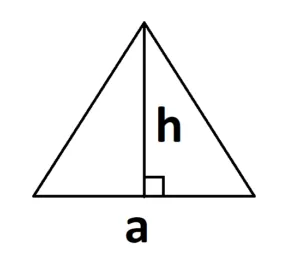Основание может быть расположено иначе, например так: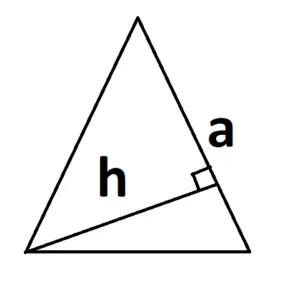При тупом угле высоту можно отразить на продолжение основания: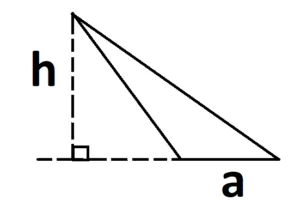При прямом угле основанием и высотой будут его катеты: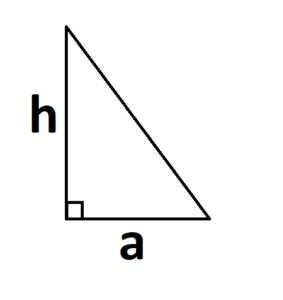
Если известны две стороны и синус угла. S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
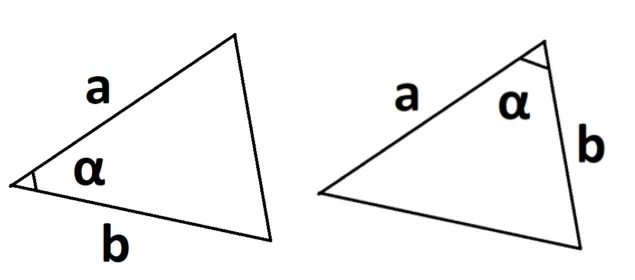
Если есть радиус описанной окружности. S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
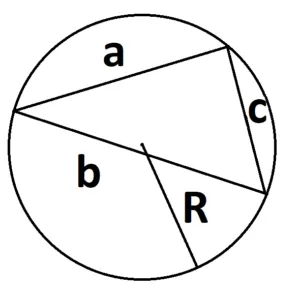
Если есть радиус вписанной окружности. S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

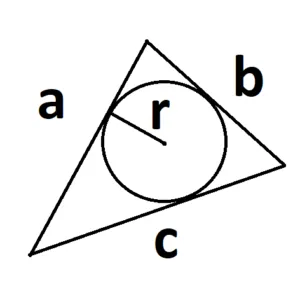
Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длины сторон.

Формула для измерения периметра равностороннего треугольника — это длина стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг

Окружность — это часть плоскости, которая лежит внутри круга.

Окружность — это граница круга.

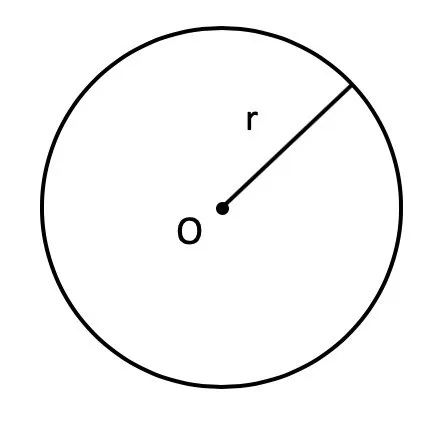
Радиус окружности — это расстояние между центром окружности и любой ее точкой.

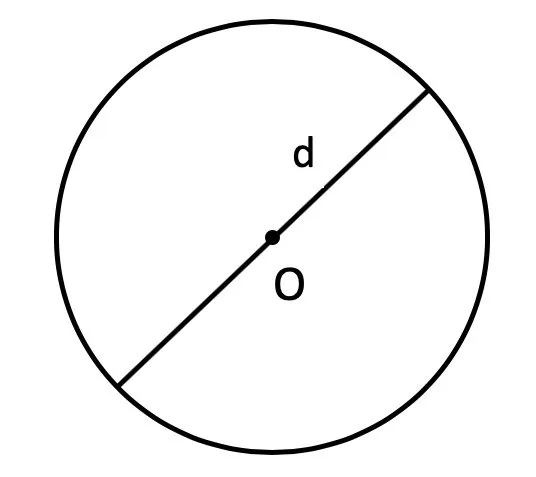
Диаметр окружности — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен двум радиусам.

Формулы для площади круга :

S = π × r 2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14 .
S = π × d 2 : 4, где d — это диаметр.
S = L 2 : (4 × π), где L — это длина окружности.

Окружность круга или длина окружности равна произведению радиуса на два пи или произведению диаметра на пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, а π — константа, выражающая отношение окружности к диаметру и всегда равная 3,14.

Фигура призма

Эта геометрическая фигура получается, если взять два многогранника, расположить их параллельно друг другу в разных пространственных плоскостях и соединить их вершины соответствующим образом. В результате получится призма, два многогранника называются ее основаниями, а грани, соединяющие эти многогранники, имеют форму параллелограммов. Призма называется прямолинейной, если ее стороны (параллелограммы) прямоугольные.

Фигура 3D из картона

Давайте попробуем свои силы в искусстве 3D-моделирования из бумаги и сделаем несколько яблок, которые украсят вашу гостиную.

Для этого необходимо следовать инструкциям шаг за шагом:

Сделайте несколько заготовок в форме яблок из цветного картона. Образцы вы можете найти в интернете или нарисовать вручную.

Вырежьте их из плотного картона, желаемого цвета. Для одного яблочка вам понадобится от 6 до 8 штук.
Сложите все заготовки пополам и смажьте клеем с противоположной стороны.

Добавьте сверху черенок из темного картона и ваше яблочко готово!

Вы можете сделать много разноцветных яблок, положить их в плетеную корзину и сделать украшение для стола. Или развесьте их, чтобы создать ощущение яблоневого сада.

Что такое геометрические фигуры?

Наука геометрия включает в себя двухмерные фигуры и трехмерные фигуры.

Они изучаются в планетометрии. Точка также является плоской фигурой.

Объемные формы хорошо известны:

Читайте также: Поделки из цветной бумаги: лучшие идеи и пошаговые инструкции по изготовлению игрушек и декоративных элементов (115 фото).

Фигуры также содержат точки.

Кстати, о геометрических фигурах: Существуют две постоянные группы, такие как:

1) Двухмерные формы,

2) Трехмерные формы.

Итак, в первую очередь для двухмерных, таких как фигуры типа:

Что касается трехмерных фигур, то они следующие:

Плоские (2D) фигуры классифицируются таким образом:

Объемные (3D) фигуры классифицируются следующим образом:

Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, сфера, додекаэдр, конус, октаэдр, призма и шар. Есть также вырезанные формы (пирамида, конус). В зависимости от площади основания пирамида или призма подразделяется на треугольники, тетраэдры и т.д.

Детские игрушки (пирамидки, мозаики и другие) позволяют знакомить детей с геометрическими трехмерными фигурами с самого раннего возраста. А плоские формы можно рисовать и вырезать из бумаги.

Из двумерных можно отметить следующие:

Трехмерные немного сложнее:

1 Из двухмерных фигур:

Круг, треугольник, квадрат, ромб, прямоугольник, трапеция, параллелограмм, овал и многоугольник. Также звезда (пентаграмма), если это можно назвать формой.

2 Трехмерные формы:

Призма, пирамида, параллелограмм, призма, сфера, цилиндр, полусфера (полусфера означает шар, разрезанный пополам) и конус. Пирамиды делятся на треугольники, квадраты и так далее (почти до бесконечности). Чем больше углов у основания пирамиды, тем больше она похожа на конус.

Двумерные фигуры (2D): углы; многоугольник (различные многоугольники: треугольник, четырехугольник, различные квадраты: параллелограмм, прямоугольник, ромб, квадрат, трапеция, дельтоид, пятиугольник, шестиугольник и т.д. на бесконечности); окружность, круг, сегмент круга, сектор круга, сектор круга, эллипс, овал.

Трехмерные формы: Двугранный угол, угол многогранника, многогранник (Разновидности многогранников: Разновидности призм: параллелепипед, куб, антипризма, пирамида, тетраэдр, усеченная пирамида, бипирамида, октаэдр, додекаэдр, икосаэдр, клин, обелиск), цилиндр, усеченный цилиндр, сегмент цилиндра (также цилиндрическая подкова или копыто), конус, усеченный конус, сфера, сегмент сферы, сферический слой, сферический сектор, эллипсоид, геоид.

С самого начала на уроках геометрии мы изучаем простые фигуры, которые являются плоскими, т.е. лежат в плоскости.

Затем открывается мир трехмерных фигур, которые нужно понять, как они расположены и как их нарисовать, чтобы они были понятны не только вам, но и другим.

Поэтому вы можете изучить приведенный ниже список основных форм.

Наконец, мне пришлось объяснять своим внучкам и внуку, какими могут быть геометрические фигуры.

Любой опытный фотограф или художник скажет вам, что бывает очень трудно правильно использовать различные типы линий в композиции. Однако это вполне возможно. И сходящиеся, и параллельные линии можно и нужно эффективно использовать в композиции изображения! Такие линии особенно эффективны в композиции фона. Взгляните на этот снимок. Вы можете легко увидеть, что линии сходятся и параллельны. Они очень хорошо привлекают внимание зрителя к главному объекту — человеку, сидящему в траве. Кроме того, эти линии визуально отражают друг друга.

Сходящиеся и параллельные линии

Вы можете использовать множество различных стилей и форм, чтобы создать что-то свое. Например, можно использовать фигуры, создающие иллюзию отражения, как в данном случае. Различные эффекты и иллюзии могут быть достигнуты путем сочетания различных форм, освещения и цветов, и есть много материала, с которым можно работать.

Если вы хотите добавить больше смысла в свою фотографическую работу, чтобы усилить эмоциональное воздействие на зрителя, то вам следует попытаться понять, как понимается пространство. В некоторых случаях фотография на первый взгляд может показаться довольно простой. Например, эти. Что здесь самое главное? Правильно. Близость зрителя к скамейке, указанной автором, и наличие пространства, вернее, пустоты, сразу за ней. Такая синтетическая конструкция кадра позволяет зрителю реконструировать историю сюжета в собственном сознании и подсознании, основываясь на собственном опыте, собственных чувствах и эмоциях.

Отношение и баланс пространства

Не тратьте время на то, чтобы понять все, что мы вам сегодня рассказали. Постарайтесь понять, как геометрические элементы влияют на композицию картины на плоскости. Вы можете прийти к этому пониманию не сразу. Но это не страшно. Главное — думать, что в какой-то мере мы посеяли семя. Нужно просто ждать, пока семя взойдет, и через некоторое время оно принесет плоды.

Сами узоры прекрасны, а узоры, используемые для соединения изображений, еще лучше. Особенно когда все узоры связаны между собой. Возьмем, к примеру,

Создайте тему

. Все картины связаны между собой похожими цветами и узорами. Выбрав узор и правильно его использовав, можно связать воедино ранее разрозненные предметы и идентифицировать продукцию как «вашу».