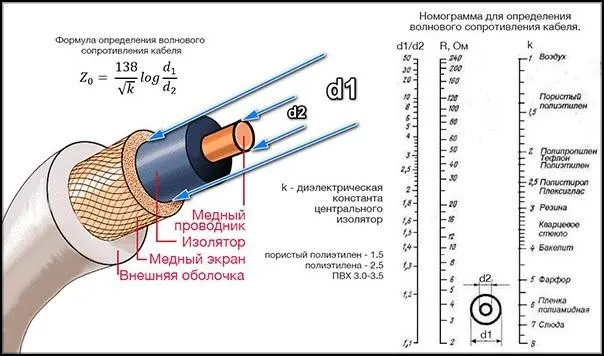
В начале моего увлечения электроникой я часто слышал о характеристическом сопротивлении коаксиального кабеля 50 Ом. Главный проводник, изолятор, оплетка, изолятор. Оплетка полностью закрывает центральный проводник. Такой кабель используется для передачи слабых сигналов, а оплетка защищает сигнал от помех.
Записки программиста
Радиолюбители находятся в постоянном поиске антенн, идеально подходящих для определенных условий. Теоретические знания, конечно, важны в этом процессе, но никакая теория не может заменить личный опыт. Поэтому ничего не остается, как снова и снова тестировать различные антенны, взвешивать их сильные и слабые стороны и делать выводы. Именно этим мы и займемся сегодня. На этот раз мы будем экспериментировать с различными антеннами из двухжильного кабеля.
Двухпроводная линия состоит из двух параллельно идущих проводов. Как и любой провод, двухпроводная линия характеризуется рядом свойств, наиболее важными из которых являются (1) характеристический импеданс, (2) коэффициент укорочения и (3) потери на единицу длины на заданной частоте. Есть, конечно, и другие свойства, такие как емкость, стоимость, вес и т.д.
Что такое характеристическое сопротивление (характеристический импеданс)? Предположим, что мы подключили источник переменного тока с известным постоянным напряжением к одному концу линии и добились того, что сигнал не отражается на другом конце. Этого можно достичь различными способами. Например, мы можем сделать линию настолько длинной, что сигнал будет полностью ослаблен потерями. В источнике по линии течет ток, который можно измерить. Теперь вспомните закон Ома и разделите напряжение на силу тока. Это волновое сопротивление линии. Оказывается, характеристический импеданс не меняется с частотой сигнала и в целом полностью зависит от физических свойств линии — используемых материалов, толщины проводников, расстояния между ними и т.д. Сопротивление коаксиального кабеля обычно составляет либо 50 Ом (кабели RG58 и RG213), либо 75 Ом (например, RG59, RG6).
Коэффициент укорочения (КУ) — это отношение скорости распространения сигнала в кабеле к скорости света в вакууме. Типичное значение VF составляет от 0,65 до 0,99. Предположим, вы знаете, что конкретная антенна для 40-метрового диапазона (7,0-7,2 МГц) должна питаться от линии с характеристическим сопротивлением 75 Ом и длиной λ/4. Используя формулу, мы делим скорость света на частоту и получаем:
Однако, поскольку сигнал распространяется в линии медленнее, чем свет в вакууме, эффективная длина намного меньше:
Интересным свойством линии длиной λ/4 является то, что она преобразует чистый активный входной импеданс антенны RLв чисто активный импеданс Z02 /RLгде Z0— волновое сопротивление линии. Такая линия называется четвертьволновым трансформатором. Например, петлевая антенна имеет входной импеданс около 106-117 Ом, в зависимости от ее формы. Это сопротивление может быть преобразовано в ~50 Ω с помощью кабеля RG59 сечением l/4, который имеет характеристический импеданс 75 Ω:
>>>75*75/106 53.06603773584906>>>75*75/117 48.07692307692308
Приложение: Работа четвертьволнового трансформатора наглядно показана на чертежных схемах Wolpert-Smith в материале Python.
Не менее интересны линии, длина которых кратна λ/2. Когда антенна с определенным входным импедансом подключена к одному концу такой линии, второй конец имеет тот же импеданс, независимо от импеданса самой линии. Такая линия называется полуволновым усилителем.
Что касается потерь в линии, то мы уже рассматривали этот вопрос в статье Выход на радиолюбительские диапазоны 2м и 70см:
Как измерить волновое сопротивление и КУ линии?
Настоящие двухпроводные радиолюбительские линии можно приобрести в специализированных интернет-магазинах, а также на eBay по таким запросам, как «450 Ohm Ladder Line» и «MFJ-18H250». Однако цены на такие линии составляют примерно от 1,5 до 3 долларов за метр, что несколько дороговато. Поэтому двухпроводные линии часто изготавливаются из существующих проводов и стержней самостоятельно, либо используются линии, предназначенные для несколько иных целей. В качестве примеров доступных двухпроводных линий можно привести П-274М («поле», около $0,17 за метр), ТПП 2х0,4 («телефонная лапша», около $0,06 за метр), различные варианты акустических кабелей (~0,23 долл. за метр). На eBay вы найдете множество предложений по запросу «акустический кабель» (около $0,75 за метр, в зависимости от толщины кабеля).
Недостатком этих кабелей является неизвестный импеданс и импеданс волн. Вопрос в том, как их можно измерить?
Волновое сопротивление может быть измерено по крайней мере двумя способами. Первый способ заключается в следующем. Вы берете несколько линейных измерителей и измеритель RLC. Устройство подключается к одному концу линии и измеряется емкость C. Затем провода линии подключаются к другому концу линии и измеряется индуктивность L. Характеристический импеданс определяется по формуле Z = sqrt(L/C).
Забавный факт! Упомянутая ранее емкость не превышает C на единицу длины линии. Например, один метр коаксиального кабеля RG58 имеет емкость около 100 пФ. Мы уже использовали этот факт в конструкции ловушек для диполя.
Для второго метода нам понадобятся осциллограф, генератор сигналов и мультиметр. К осциллографу подключается Т-образный BNC-разъем. К одному из входов вилки подключается генератор, а к другому — часть измеряемой линии. Ко второму концу линии подключен потенциометр. Генератор сигнала производит меандр, а ручка потенциометра перемещается в положение, при котором осциллограф отображает сигнал без искажений. Когда такое положение найдено, это означает, что в линии нет отражений. Это возможно только в том случае, если потенциометр имеет сопротивление, равное сопротивлению линии. Остается только взять мультиметр и измерить полученное сопротивление потенциометра. Эта процедура наглядно продемонстрирована в видеоролике Алана Вольке, W2AEW.
Однако следует отметить, что оба метода далеки от совершенства. Практика показывает, что погрешность измерения составляет порядка 5%.
Используя ту же технику и осциллограф, мы можем определить линию CG. Если мы отключим потенциометр, сигнал полностью отразится на конце линии. С помощью осциллографа мы можем измерить время, необходимое сигналу, чтобы дважды пройти по линии (время возврата). Длина линии известна, поэтому мы можем измерить скорость распространения сигнала. Разделите его на скорость света, чтобы получить МЭД.
Если у вас нет осциллографа, вы можете измерить КУ с помощью КСВ-метра и эквивалента нагрузки 50 Ом. Возьмите отрезок шнура длиной 5 м. Подключите один конец к измерителю КСВ, а другой — к эквивалентной нагрузке. Затем найдите минимальный КСВ в диапазоне 15-30 МГц. В результате нужно найти частоту, на которой КСВН равен 1 или очень близок к этому значению. На этой частоте линия действует как полуволновой усилитель, а устройство нагружено на 50 Ом. Длина линии известна, длина полуволны также известна. Соотношение первых и вторых — CG.
Простая походная антенна из двухпроводной линии
Вышеизложенная теория является фундаментальной для понимания и построения следующей антенны (рисунок заимствован из книги ARRL Antenna Book):
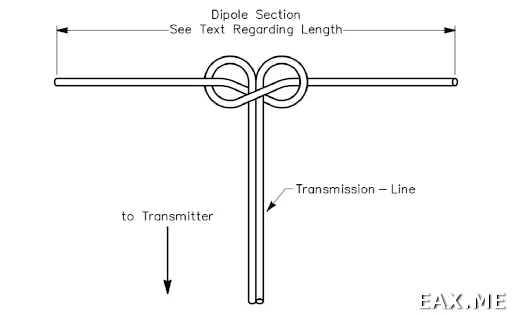
Антенна представляет собой обычный диполь, питаемый двухпроводной линией. Среди англоязычных радиолюбителей эта антенна известна как антенна из акустического провода, поскольку она часто изготавливается из акустического провода. Очевидно, что если подать диполь с входным импедансом 50-73 Ом через двухпроводную линию с волновым сопротивлением 100-600 Ом, то ничего хорошего из этого не выйдет. Однако выше мы установили, что λ/2-линия действует как полуволновой усилитель. Остается только найти подходящую линию, измерить емкость линии, обрезать линию до подходящей длины и получить очень легкий и компактный диполь. Поскольку диполь питается по двухпроводной линии, в ней не возникает синфазных токов, поэтому для такой антенны не нужен балун. Тонкий стержень можно использовать в качестве мачты без риска, что он сломается под весом балуна.
Для украшения я решил купить на eBay 30 м акустического провода 20 AWG и подключить его к диполю для диапазона 20 м. Измеренная КУ кабеля составила ~0,75. Это очень удобно, так как длина λ/2 шнура составляет 7,5 м, что как раз соответствует длине легкой и дешевой удочки.
Было решено использовать небольшую лопату для крепления столбов, а не прутья, как в прошлый раз:
Лопата представляет собой кусок алюминиевого профиля длиной полметра, отрезанный и отшлифованный с помощью Dremel. Он вставляется в землю примерно на половину своей длины. Планка крепится с помощью застежек-липучек, подобных тем, которые используются для крепления батарей на квадрокоптерах. Напротив, эта конструкция достаточно надежна (для временной установки), а по весу и занимаемому месту она значительно превосходит три тросовых шуруповерта.
Для подключения антенны к трансиверу лучше всего использовать штекер типа «крокодил» и штекер типа «банан» диаметром 4 мм:
Штекер подключается к разъему SO-239. Диаметр пробки идеально подходит к промежутку. «Крокодил» проще всего прикрепить к клемме заземления трансивера.
Точные размеры моей антенны следующие. Длина линии — 758 см. Длина одной руки составляет 490 см. Диаграмма KSV немного меняется в зависимости от высоты антенны на земле и угла между плечами, но в среднем она выглядит следующим образом:
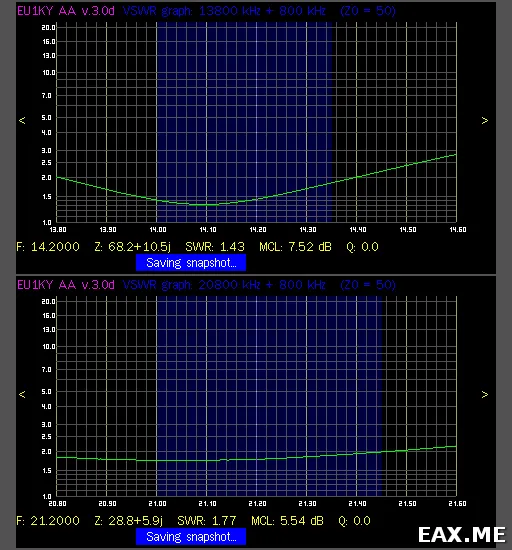
Если вы поиграете с формой и высотой антенны, то сможете добиться КСВ до единицы на 20 м. По счастливому совпадению, антенна также оказалась достаточно удобной на расстоянии 15 метров. КСВ в этом диапазоне составляет от 1,7 до 2. Радиотрафик был хорошим на всех диапазонах. С точки зрения уровня шума и принимаемых сообщений, я не заметил никакой разницы по сравнению с классическим диполем.
Забавный факт! Сложенная антенна очень компактна, поэтому имеет смысл всегда иметь ее при себе в качестве запасного варианта.
Природа волнового сопротивления
Характеристический импеданс линии передачи определяется соотношением напряжения и тока в электромагнитной волне, распространяющейся по линии передачи. Это свойство среды распространения электромагнитной волны. Импеданс любого проводника не зависит от его длины, сопротивления нагрузки на линии и выходного импеданса источника напряжения. Он определяется только конструктивными параметрами сечения линий передачи.
Для коаксиальных кабелей это диаметры центрального и внутреннего проводников и диэлектрическая проницаемость материала заполнителя. Для двухпроводной линии это расстояние между проводами, диаметр проводов и свойства материала, которым заполнен промежуток.
Математически характеристический импеданс равен входному импедансу бесконечно длинной линии с конечной нагрузкой, равной ее собственному характеристическому импедансу. Он измеряется в омах и указывает на связь между электрической и магнитной составляющими электромагнитной волны.
Хотя ток течет по проводнику почти мгновенно, каждый электрический провод или кабель имеет характерное сопротивление. Обычный электрический кабель состоит из двух изолированных друг от друга проводников. Если вы проверите омическое сопротивление между ними, оно будет бесконечным. Если вы проверите его с помощью омметра, соединив разные концы одного и того же проводника, вы обнаружите, что он равен нулю.
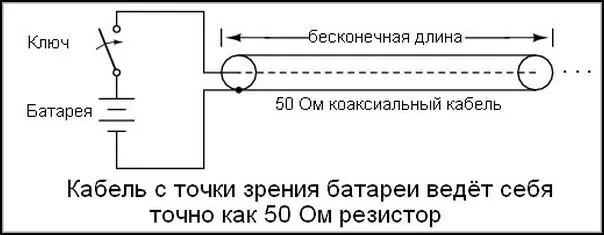
Маркировка на проводе указывает на его импеданс (сопротивление). В большинстве обычных ситуаций это примерно 50 или 75 Ом. Если вы используете омметр, вы получите результат, описанный выше. Важно понимать, что это не омическое сопротивление, а характеристический импеданс.
Виды сопротивлений в электрических цепях
В электрических цепях существует три вида сопротивления, которые отличаются по своей природе:
- активное;
- реактивное;
- полное или импеданс.
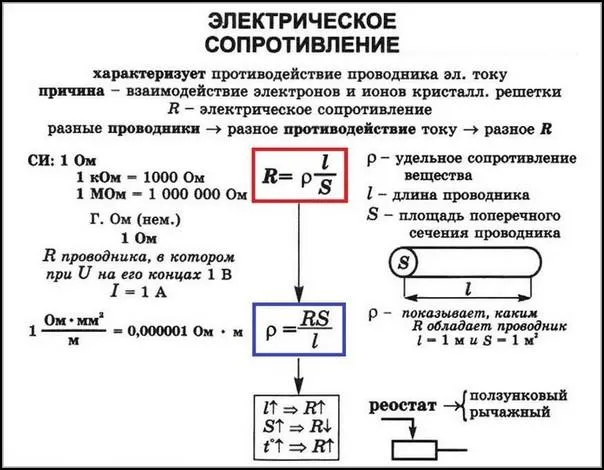
Активное сопротивление
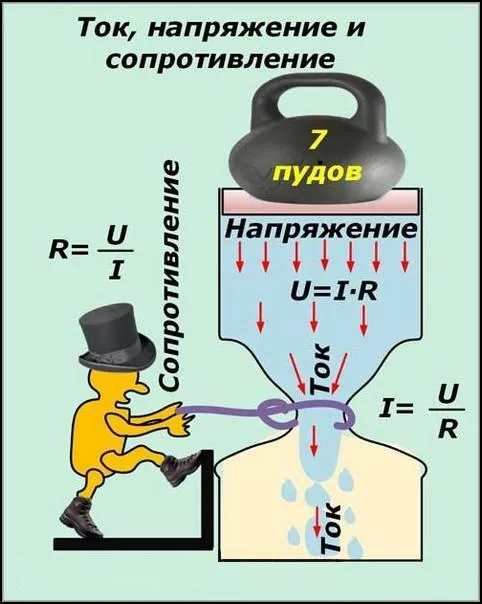
Напряжение, приложенное к цепи, вызывает ток, величина которого пропорциональна существующей разности потенциалов. Коэффициент пропорциональности между ними — это активное сопротивление, также называемое омическим сопротивлением. Если вышеприведенный пример измерялся омметром, то это было сопротивление. Значение активного сопротивления определяется по закону Ома.
Реактивное сопротивление
Если в цепи есть емкость, этот тип сопротивления называется емкостным сопротивлением. Она равна нулю, когда ток постоянен. Емкостное сопротивление возникает в цепях переменного тока, когда нет прямого контакта между компонентами.
Это сопротивление основано на том, что близлежащие, но не напрямую соединенные проводники заряжаются до определенного предела, а затем постепенно разряжаются. Таким образом, результирующий ток направлен в направлении, противоположном его первоначальному изменению.
Это свойство используется в конденсаторах. Однако следует учитывать, что емкость возникает почти в каждом соседнем токопроводящем проводнике. Это особенно верно для двух проводников, составляющих электрический кабель. Следовательно, любое изменение силы тока в них обеспечивает возникновение емкости.
Имеется также индуктивный резистор. При изменении напряжения генерируется переменное электромагнитное поле, которое индуцирует ток. Это всегда происходит в направлении, противоположном первоначальному изменению. То есть увеличение индуктивного сопротивления вызывает ток, который тормозит первоначальное изменение, и наоборот.
Этим свойством обладают индукционные катушки, но почти каждый электрический компонент имеет индуктивность, которая действует подобным образом. Это относится и к электрическим кабелям. Они обладают определенной индуктивностью, которую можно определить, и поэтому оказывают сопротивление переменному току. Индуктивное сопротивление также возникает при включении или выключении нагрузки в цепи постоянного тока.
Разница между емкостным и индуктивным сопротивлением называется реактивностью.
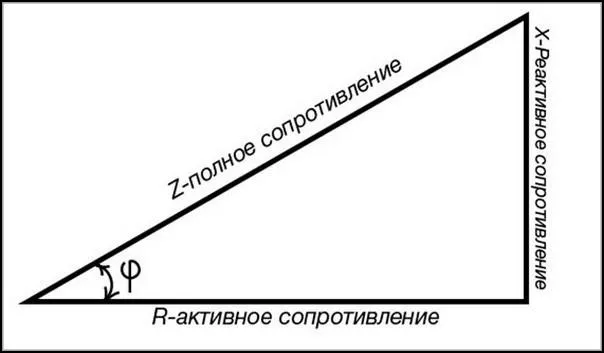
Импеданс
При определении импеданса или кажущегося сопротивления учитываются все три физических варианта сопротивления. Для этого используется прямоугольный треугольник, длина одной ножки которого представляет собой значение активного сопротивления, а другой — разницу между значениями емкостного и индуктивного сопротивлений.
Формулы для расчёта
Для электрической двухпроводной линии без потерь значение внутреннего сопротивления рассчитывается по следующей формуле.
Поскольку для определения характеристического импеданса используется концепция бесконечного проводника идеальной формы, для расчета используются формулы, учитывающие геометрические свойства и материал проводников. Ниже приведены определения, которые применяются в самых простых случаях.
Если рассматривать проводник, состоящий из двух проводников, то характеристический импеданс определяется по формуле:
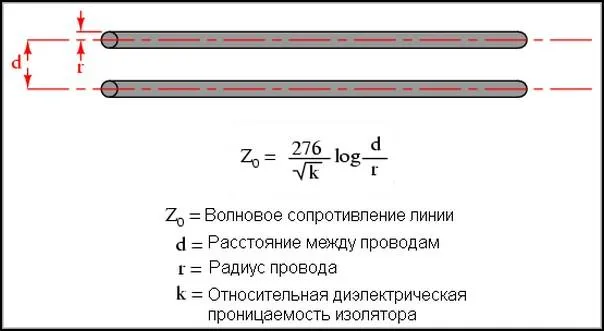
Если используются коаксиальные кабели, формула выглядит следующим образом:
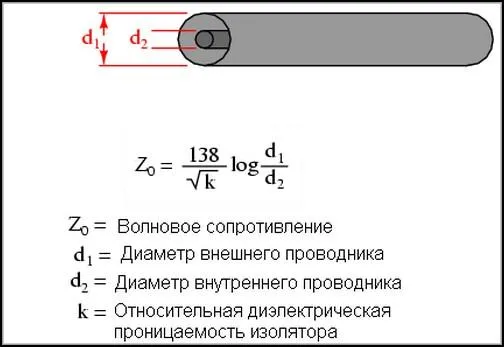
Кабели и скорость света
Рассмотрим следующую схему. Цепь замкнута — свет горит. Цепь разомкнута — свет гаснет. Лампочка загорается не сразу. По крайней мере, он должен загореться. Но я хочу сосредоточиться не на этом. Хотя электроны движутся очень медленно, они взаимодействуют друг с другом гораздо быстрее — со скоростью света.
Что произойдёт, если длина проводов будет 300 тысяч км? Так как электроэнергия передаётся с конечной скоростью, очень длинные провода внесут задержку.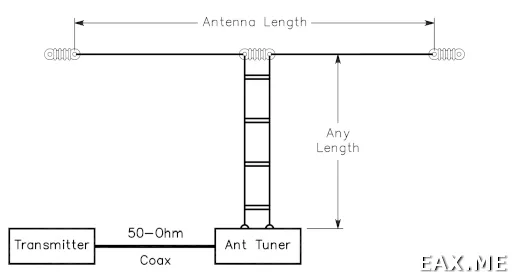
Пренебрегая временем на разогрев лампы, и сопротивлением проводов, лампа зажжётся примерно через 1 секунду после включения выключателя. Несмотря на то, что строительство сверхпроводящих ЛЭП такой длины создаст огромные практические проблемы, теоретически это возможно, поэтому наш мысленный эксперимент реален. Когда переключатель выключается, лампа будет продолжать получать питание ещё 1 секунду. Один из способов представить движение электронов в проводнике – это вагоны поезда. Сами вагоны движутся медленно, только начинают движение, и волна сцеплений передаётся гораздо быстрее.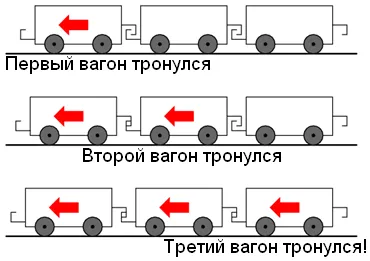
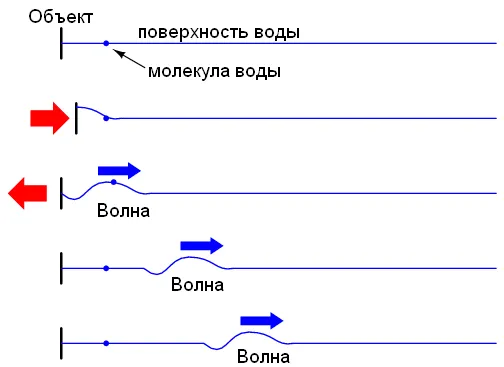
Другая аналогия, которая может подойти лучше, — это волны на воде. Объект начинает двигаться горизонтально по поверхности. Взаимодействие молекул воды создает волну. Волна движется гораздо быстрее, чем движутся молекулы воды.
Электроны взаимодействуют со скоростью света, но они движутся гораздо медленнее, как молекула воды на иллюстрации выше. При очень большой схеме задержка между щелчком выключателя и включением лампочки будет заметна.
Волновое сопротивление
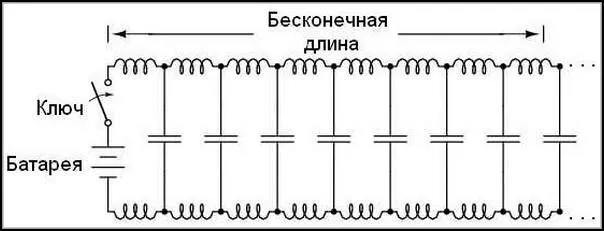
Предположим, у нас есть два параллельных провода бесконечной длины, без лампочки в конце. Потечёт ли ток при замыкании выключателя?
Несмотря на то, что наш провод — сверхпроводник, мы не можем пренебречь ёмкостью между проводами: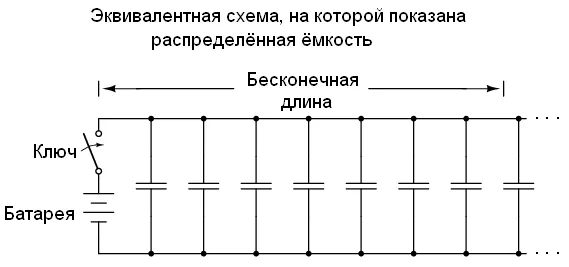
Подключите источник питания к кабелю. Ток зарядки конденсатора определяется по следующей формуле: I = C(de/dt). Следовательно, мгновенное увеличение напряжения должно вызвать бесконечный ток. Однако ток не может быть бесконечным, поскольку вдоль провода существует индуктивность, которая ограничивает увеличение тока. Падение напряжения на индуктивности определяется по формуле: E = L(dI/dt). Это падение напряжения ограничивает максимальный ток.
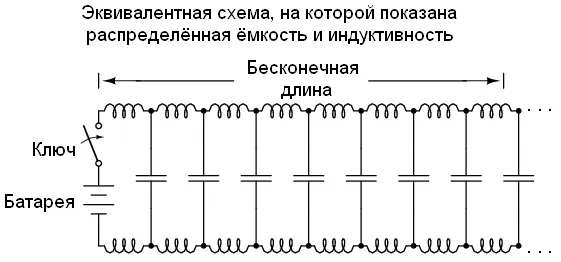
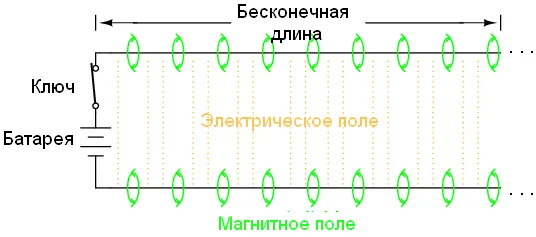Поскольку электроны взаимодействуют со скоростью света, волна будет распространяться с той же скоростью. Таким образом, нарастание тока в индуктивностях, и процесс зарядки конденсаторов будет выглядеть следующим образом:
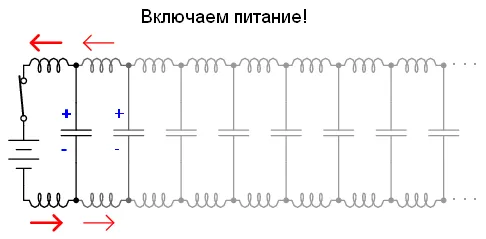
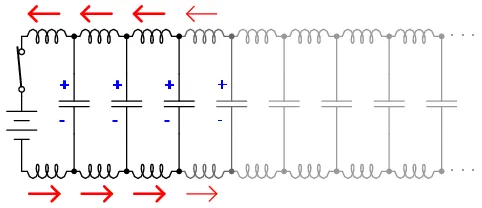
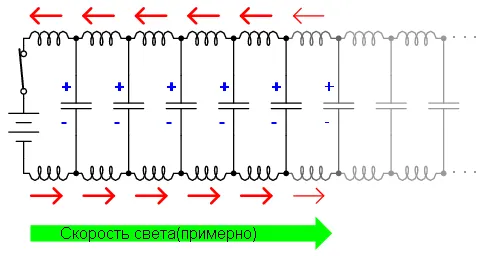
В результате этих взаимодействий, ток через батарею будет ограничен. Так как провода бесконечны, распределённая емкость никогда не зарядится, а индуктивность не даст бесконечно нарастать току. Другими словами, провода будут вести себя как постоянная нагрузка. Линия передачи ведёт себя как постоянная нагрузка так же, как и резистор. Для источника питания нет никакой разницы, куда бежит ток: в резистор, или в линию передачи. Импеданс (сопротивление) это линии называют волновым сопротивлением, и оно определяется лишь геометрией проводников. Для параллельных проводов с воздушной изоляцией волновое сопротивление рассчитывается так: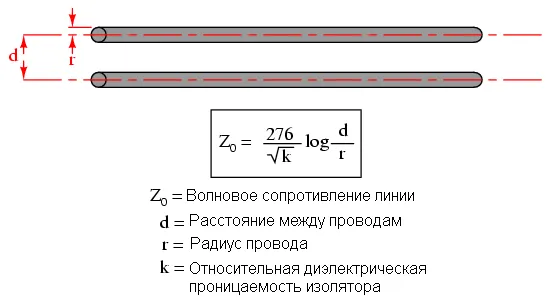
Для коаксиального провода формула расчёта волнового сопротивления выглядит несколько иначе: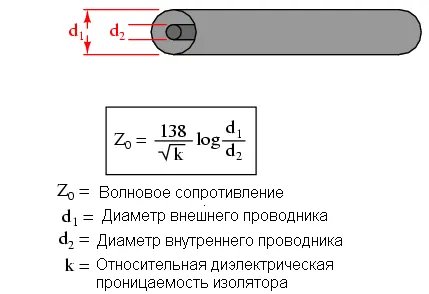
Если изолирующий материал не является вакуумом, то скорость распространения меньше скорости света. Отношение между фактической скоростью и скоростью света называется коэффициентом укорочения. Коэффициент укорочения зависит только от свойств изолятора и рассчитывается по следующей формуле:
Волновое сопротивление известно также как характеристическое сопротивление. Из формулы видно, что волновое сопротивление увеличивается по мере увеличения расстояния между проводниками. Если проводники отдалить друг от друга, становится меньше их ёмкость, и увеличивается распределённая индуктивность (меньше эффект нейтрализации двух противоположных токов). Меньше ёмкость, больше индуктивность =>меньше ток =>больше сопротивление. И наоборот, сближение проводов приводит к большей ёмкости, меньшей индуктивности =>больше ток =>более низкое волновое сопротивление. Без учета влияния тока утечки через диэлектрик волновое сопротивление должно соответствовать следующей формуле:
Линии передачи конечной длины
Линии бесконечной длины — это интересная абстракция, но она невозможна. Все линии имеют конечную длину. Если бы кусок 50-омного кабеля RG-58/U, который я измерял омметром несколько лет назад, был бесконечной длины, я бы измерил сопротивление 50 Ом между внутренним и внешним кабелями. Но этот кабель не был бесконечным и был измерен как открытый, с бесконечным сопротивлением.
Однако характеристический импеданс также важен, когда речь идет о проводе конечной длины. Когда к проводу прикладывается переходное напряжение, течет ток, равный отношению напряжения и характеристического импеданса. Это просто закон Ома. Однако он действует не бессрочно, а только в течение ограниченного периода времени.
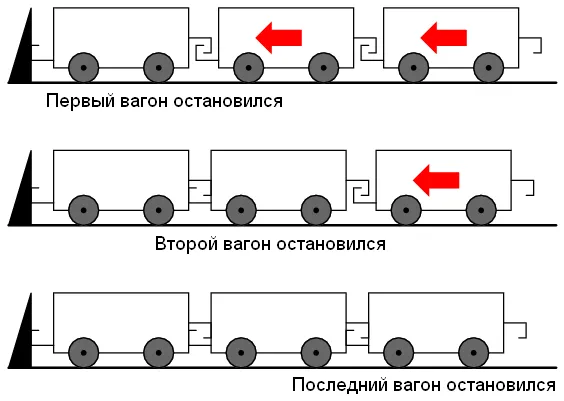
Если в конце строки есть разрыв, ток останавливается в этой точке. И это внезапное прерывание тока влияет на всю линию. Представьте себе поезд, движущийся по рельсам с расцепленной сцепкой. Когда она наезжает на стену, то останавливается не сразу: сначала первая машина, потом вторая и так далее.
Сигнал, распространяющийся от источника, называется падающей волной. Распространение сигнала от заряда обратно к источнику называется отраженной волной.
Как только стопка электронов в конце линии стекает обратно в батарею, ток в линии прекращается и ведет себя как обычная разомкнутая цепь. С проводами разумной длины все это происходит очень быстро, поэтому омметр не успевает измерить сопротивление. У него нет времени, чтобы измерить продолжительность времени, в течение которого цепь ведет себя как резистор. Для километрового кабеля с коэффициентом отсечки 0,66 время прохождения сигнала составляет всего 5,05 мс. Отраженная волна возвращается к источнику за то же время, т.е. всего за 10,1 мс.
Высокоскоростные измерительные устройства способны измерить это время между передачей сигнала и приходом отражения для определения длины кабеля. Этот метод также можно использовать для определения обрыва одного или обоих проводов кабеля. Эти устройства называются кабельными рефлектометрами. Основной принцип такой же, как и в ультразвуковом сонаре: генерировать импульс и измерять время резонанса.
Аналогичное явление происходит в случае короткого замыкания: Когда волна достигает конца кабеля, она отражается обратно, поскольку между двумя соединенными кабелями не может быть напряжения. Когда отраженная волна достигает источника, источник определяет, что произошло короткое замыкание. Все это происходит за то время, которое требуется сигналу, чтобы пройти туда и обратно.
Простой эксперимент иллюстрирует явление отражения волн. Возьмите веревку, как показано на рисунке, и потяните за нее. Волна начинает распространяться до тех пор, пока ее полностью не погасит трение.
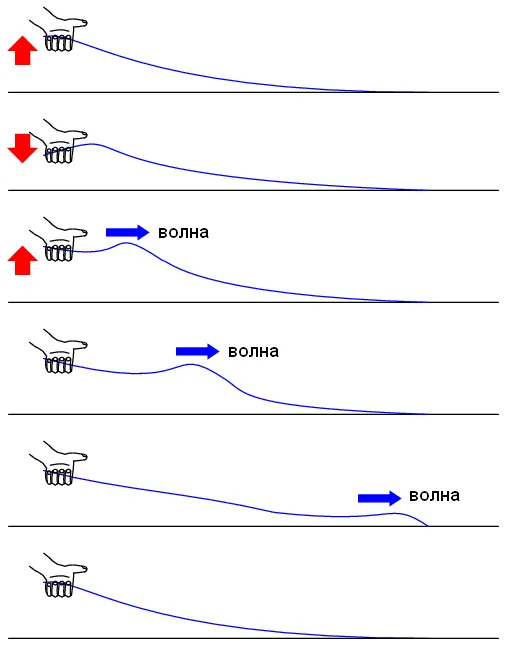
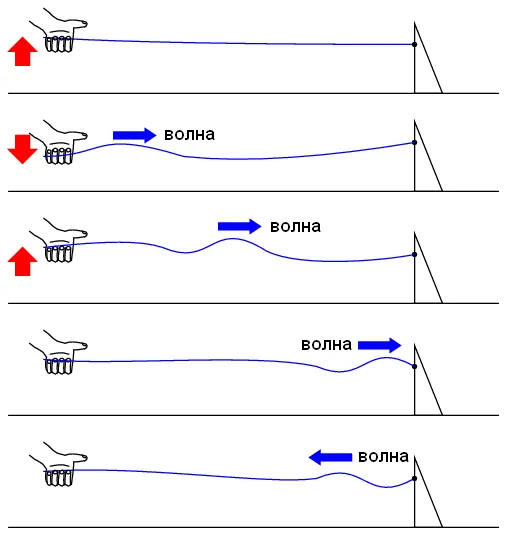
Это похоже на длинную змею с потерями. Уровень сигнала уменьшается тем больше, чем дальше вы продвигаетесь по линии. Однако если другой конец прикреплен к твердой стене, вы получите отраженную волну:
В целом, назначение линии передачи заключается в передаче электрического сигнала из одной точки в другую.
Назначение линии передачи заключается в передаче сигнала в провод для достижения цели линии передачи: Назначение линии передачи заключается в передаче сигнала из одной точки в другую. Отражения могут быть устранены, если оконечное сопротивление в линии точно равно волновому сопротивлению. Например, разомкнутая или закороченная линия отражает весь сигнал обратно к источнику. Однако если в конце линии установлен резистор 50 Ом, вся энергия поглощается резистором.
Коэффициент отражения
Соотношение между комплексными ширинами напряжения (тока) падающей и отраженной волн различно в разных частях линии. Можно вывести эти коэффициенты из системы (23.8), регулируя коэффициенты тока и напряжения по току
Из системы (24.11) по правилу Крамера получаем константы
Подставляя значения, найденные в (24.9), получаем частичное решение:
(24.12)
Система уравнений (24.12) позволяет вычислить отношение комплексных ширин напряжений и токов отраженной и падающей волн на поперечном сечении линии на расстоянии
(24.13)
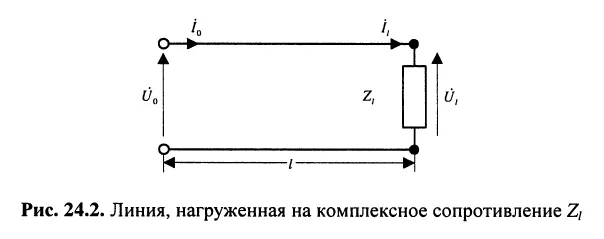
Однако для выбранного направления считывания (рис. 24.2) напряжение имеет следующее уравнение
(24.14)
Определение:
(24.15)
Отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.
Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:
1. коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии.
2. коэффициент отражения тока отличается от коэффициента отражения напряжения только знаком.
3. при p = 0 отраженная волна отсутствует. Линия, импеданс нагрузки которой равен волновому сопротивлению, называется согласованной нагрузкой, а импеданс нагрузки — согласованным импедансом. Любая другая нагрузка приведет к появлению отраженной волны на линии.
(4) Отношение ширин отраженной и падающей волн (см. (24.14) и (24.15))
уменьшается по мере продвижения от конца линии к ее началу. 5.
5. в области короткого замыкания, когда p = -1, а коэффициент отражения тока p = 1. Это означает, что отраженное и падающее напряжения на конце линии находятся в противофазе:
и результирующее напряжение равно нулю
а токи падающей и отраженной волн находятся в фазе
и результирующий ток в два раза больше падающего тока.
6. Таким образом, в области холостого хода, когда p = 1, ситуация противоположна выводу пункта 5: напряжения отраженной и падающей волн на конце линии находятся в фазе:
а результирующее напряжение равно удвоенному напряжению падающей волны
и ток равен нулю
Уравнения передачи согласованно нагруженной длинной линии
Ранее (см. раздел 23.3) были выведены уравнения передачи для длинной линии (23.8), которые являются общим решением телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения большинства практических задач достаточно знать только соотношения между напряжениями и токами на внешних зажимах линии и не интересоваться законом распределения напряжений и токов вдоль линии. Другими словами: На практике достаточно рассматривать линию как согласованный квадруполь, который полностью описывается соответствующими уравнениями передачи.
Мы поставили перед собой задачу найти уравнения передачи согласованной линии, соединяющей комплексные амплитуды напряжений и токов на ее внешних зажимах.
Используем уравнения (24.12) для комплексных амплитуд напряжения и тока падающей и отраженной волн и подставим их в систему (24.9):
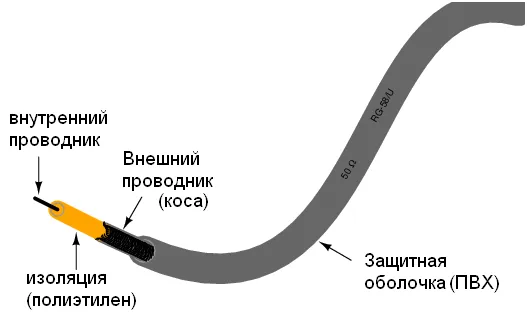
(24.16)
Подставляя выражения (24.14) в систему (24.9), получаем
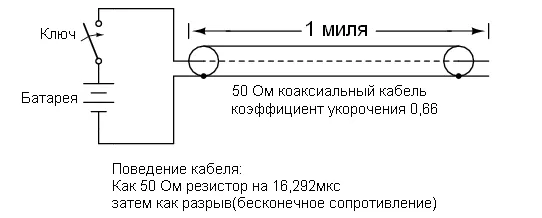
(24.17)
Системы (24.16) и (24.17) являются системами уравнений переноса длинной линии. Обычно комплексные амплитуды напряжения и тока на входных клеммах линии (x = 0) обозначаются следующим образом.
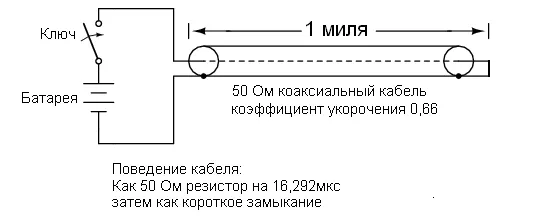
(24.18)
В большинстве случаев уравнения (24.8) записываются в более компактной форме:
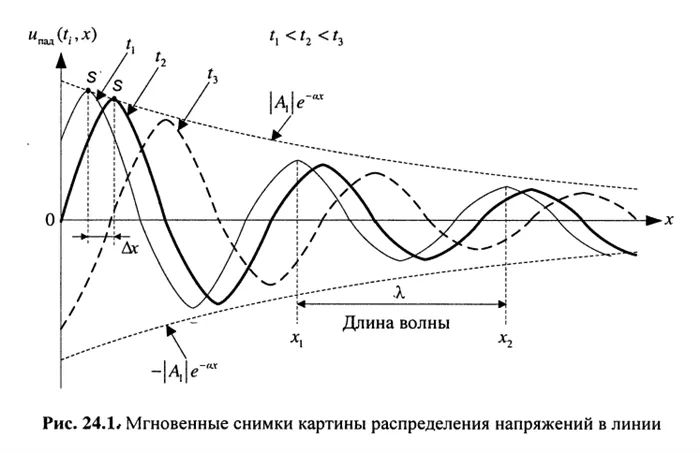
(24.19)
Где
Для работы адаптивной нагрузки, т.е. когда нет отраженной волны, из (24.18) получаем уравнения передачи адаптивной линии нагрузки:
Именно в такое состояние желательно привести линию связи, поскольку отраженные волны вызывают ряд нежелательных эффектов, о чем будет рассказано ниже.
Постоянная передачи и частотные характеристики длинной линии
Константа передачи длинной линии:
Определение
Безразмерная комплексная величина, соответствующая произведению коэффициента распространения
называется постоянной линии передачи.
Действительная часть константы передачи представляет собой естественное, волнообразное или характерное затухание линии, а мнимая часть — естественную, волнообразную или характерную фазу.
Константа передачи и ее параметры характеризуют линию как таковую и не зависят от характеристик генератора и нагрузки, между которыми линия может быть переключена.
Поскольку режим адаптивной нагрузки является типичным для линии, приведенные выше параметры мы найдем только для этого режима.
В этом случае константа переноса может быть найдена из логарифма уравнения (24.20):
(24.22)
Если подставить комплексное отношение амплитуд
под знаком логарифма, получаем:
на основе которых можно записать два одинаковых выражения для коэффициента распространения
Затухание линии
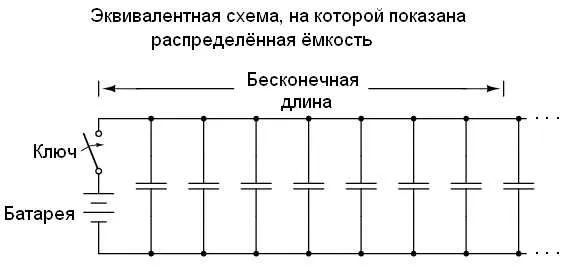
(24.3)
и собственная фаза
Из выражений (24.23) и (24.24) следует, что для когерентно заряженной линии
Собственное затухание линии
Естественная фаза линии равна разности между начальными фазами входного и выходного напряжений и токов.
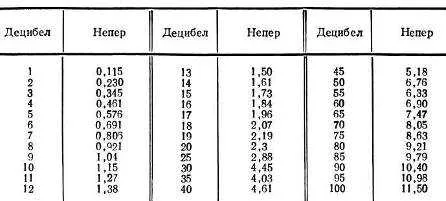
Естественное затухание линии часто выражается в децибелах:
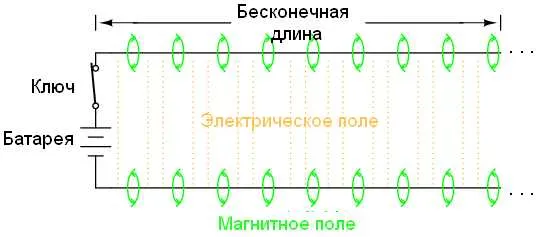
(24.25)
В этом случае нетрудно переформулировать соотношение естественного затухания, выраженное в децибелах, используя десятичные логарифмы соотношений амплитуд напряжения (тока) или суммарных мощностей.
Пример 24.1.
Оцените потери мощности телевизионного сигнала при его распространении в фидерной линии от антенной системы до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на участках магистральной линии между магистральными усилителями (рис. 24.4).
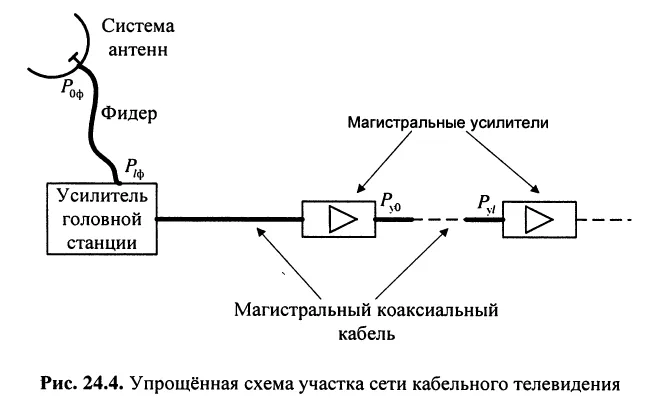
Решение. Затухание источника питания зависит от его конструкции, длина которой измеряется на средней частоте полосы питания. Типичный кабель электропитания имеет длину 50-150 м. Типичным кабелем, используемым при разработке источников питания, является РК-75-24-51, который имеет полосу пропускания 50-600 МГц и коэффициент затухания = 100, а его естественное затухание (24,25) равно
а коэффициент мощности сигнала на выходе питающего устройства равен
т.е. потери мощности в фидере низкие.
Фидер — это линия для передачи высокочастотных электрических колебаний от радиопередатчика к антенне и от антенны к радиоприемнику.
Прежде чем читать статью, подумайте над следующим вопросом: Если вы подключите очень длинный кабель (более 300 000 километров, сверхпроводник) к батарее, а противоположные концы кабеля нигде не соединены, потечет ли ток? Сколько ампер? Прочитав эту статью, вы поймете концепцию характеристического импеданса. На лекциях по теории волн я узнал только то, что характеристический импеданс — это сопротивление волнам. Большинство студентов, похоже, понимали совершенно одинаково. То есть, ничего.
Эта статья является очень вольным переводом Lessons In Electric Circuits.
На Хабре: связь доступна, сигнала нет Мусор на Википедии: длинная очередь.
Что случилось.
На заре своего увлечения электроникой я часто слышал о 50-омном сопротивлении коаксиального кабеля. Коаксиальный кабель состоит из двух проводов. Центральный провод, изолятор, жгут, изолятор. Оплетка полностью закрывает центральный провод. Такой кабель используется для передачи слабых сигналов, а оплетка защищает сигнал от помех.
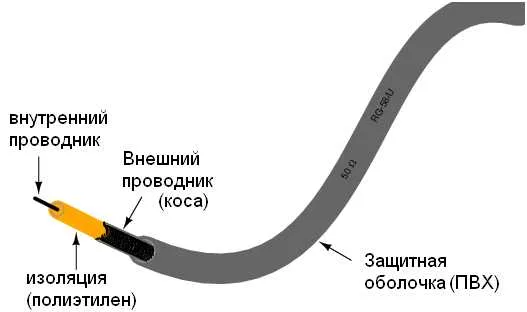
Эта надпись — 50 Ω — озадачила меня. Как между двумя изолированными проводниками может быть сопротивление 50 Ом? Я измерил сопротивление между проводами и, как и ожидалось, увидел обрыв. Сопротивление кабеля с одной стороны на другую равно нулю. Независимо от того, как я подключал омметр, я все равно не мог найти резистор 50 Ом. В то время я не понимал, как проволока реагирует на импульсы. Омметр, конечно же, работает с постоянным током и показывает, что проводники не соединены друг с другом. Но провод действует как резистор из-за влияния емкостей и индуктивностей, распределенных по проводу. И так же, как у обычного резистора, ток пропорционален напряжению. То, что мы видим как пару проводников, является важным элементом цепи для высокочастотных сигналов. В этой статье вы узнаете, что такое соединительная линия. Многие из эффектов линий связи не проявляются при постоянном токе или частоте сети 50 Гц. Однако в высокочастотных цепях эти эффекты очень важны. Практическое применение линий электропередач — это радиосвязь, компьютерные сети и низкочастотные цепи для защиты от перепадов напряжения или ударов молнии.
Кабели и скорость света
Рассмотрим следующую схему. Цепь замкнута — свет горит. Цепь разомкнута — свет гаснет. Лампа загорается не сразу. По крайней мере, он должен загореться. Но я хочу сосредоточиться не на этом. Хотя электроны движутся очень медленно, они взаимодействуют друг с другом гораздо быстрее — со скоростью света.
Что произойдет, если длина проводов составит 300 000 км? Поскольку электричество передается только с определенной скоростью, очень длинные провода вызывают задержку.
Если не учитывать время нагрева лампы и сопротивление проводов, то лампа загорается примерно через 1 секунду после включения выключателя. Хотя на практике строительство сверхпроводящих линий электропередач такой длины вызовет огромные проблемы, теоретически это осуществимо, поэтому наш мысленный эксперимент реалистичен. При выключении выключателя лампа остается включенной в течение 1 секунды. Один из способов представить движение электронов в проводнике — это перемещение их по вагонам поезда. Сами автомобили движутся медленно, как только они начинают движение, а волна сцепления передается гораздо быстрее.
Волновое сопротивление
Характеристическое сопротивление — это сопротивление, с которым сталкивается электромагнитная волна при распространении по однородному проводнику без отражения:
Где U n и I n — напряжение и ток падающей волны,
U от и I от совпадают с отраженной волной.
Поэтому величина характеристического импеданса не зависит от длины кабельной линии и постоянна в каждой точке цепи.
В общем случае характеристический импеданс является комплексной величиной и может быть выражен действительной и мнимой частями:
В таблице 3-1 приведены формулы для расчета Z в a i b.
Характеристический импеданс коаксиального или однополярного кабеля в металлической оболочке
В изоляционных материалах, диэлектрическая проницаемость которых почти не зависит от частоты,
где 3335,8 — постоянный коэффициент уменьшения длины волны МЭК.
При разработке высокочастотных кабелей целью является достижение оптимальной конструкции, обеспечивающей высокие электрические характеристики при минимально возможном использовании материала. Например, если для внутреннего и внешнего проводников высокочастотного кабеля используется медь, то минимальное затухание достигается при, Ом, максимальная электрическая мощность при, Ом, а максимальная передаваемая мощность при, Ом.
Точность и стабильность параметров кабеля зависят от значений допусков на внутренний и внешний диаметр проводника и стабильности e.
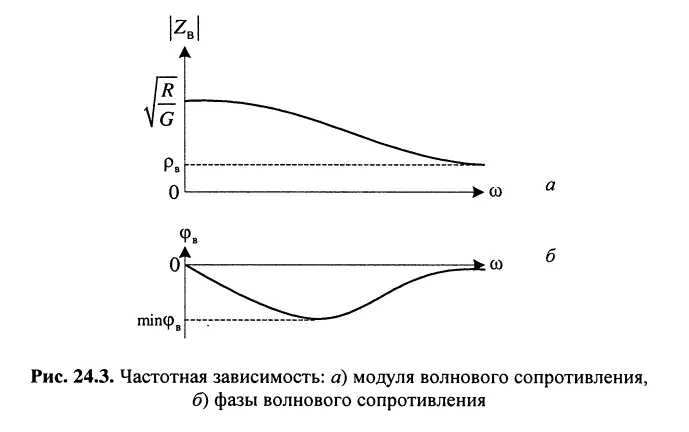
Характеристическое сопротивление симметричного кабеля в зависимости от частоты показано на рисунке 3-7. 3-7. Модуль волнового сопротивления Z B уменьшается с частотой от f = 0 до и остается постоянным в высокочастотном диапазоне. Угол характеристического импеданса равен нулю при f = 0 и на высоких частотах. На тональных частотах (f ≈ 800 Гц) угол волнового сопротивления наибольший. Для кабельных линий преобладает емкостная составляющая характеристического импеданса, поэтому угол характеристического импеданса всегда отрицательный и не превышает 45°.
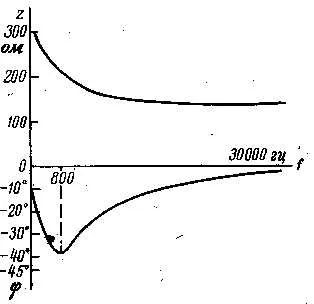
Рисунок 3-7. Частотная зависимость характеристического импеданса симметричного кабеля.
В кабельной линии с однородными электрическими свойствами на всем пути от генератора до приемника, с нагрузкой на концах, сопротивление которой равно характеристическому сопротивлению (Z r = Z n = Z B), вся передаваемая электромагнитная энергия полностью поглощается приемником без отражения.
В неоднородных линиях и с несогласованными нагрузками отраженные волны возникают в точках электрического рассогласования, и часть энергии возвращается в начало линии. Передаваемая энергия значительно ниже при нерезонансной нагрузке, чем при резонансной.
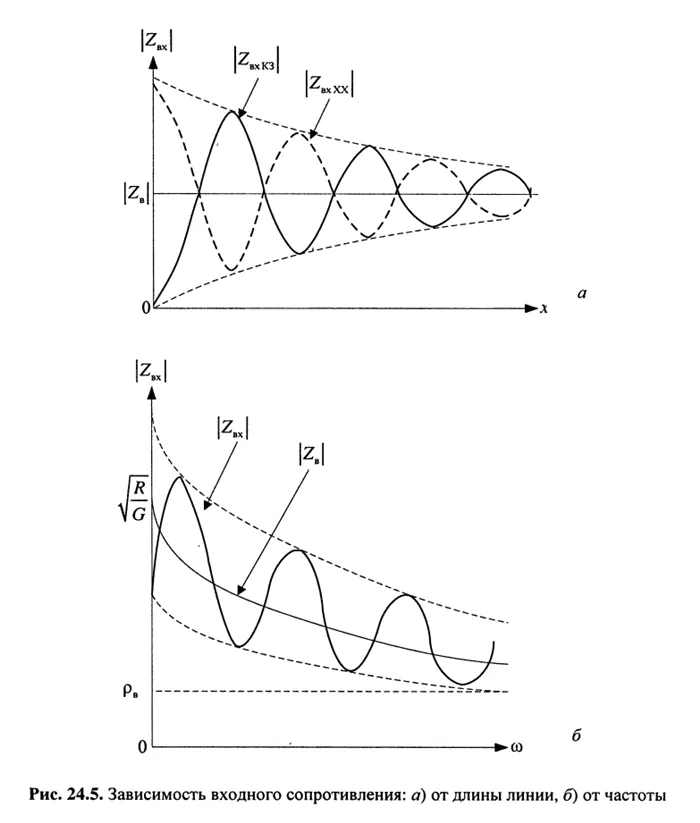
Отраженные волны искажают частотную характеристику волнового сопротивления самого кабеля. В этом случае речь идет не о характеристическом сопротивлении на входе кабеля, а о входном сопротивлении Z в .
Отношение между энергией, поступающей в приемник, и отраженной энергией зависит от импеданса приемника Z B и характеристического импеданса Z B и задается коэффициентом отражения
При согласованной нагрузке (Z n = Z in ) коэффициент отражения равен нулю, и энергия полностью поглощается приемником. В состоянии короткого замыкания (Z n = 0) и в состоянии инерции (Z n = ∞) коэффициент отражения равен — 1 и + 1 соответственно.
Для обеспечения хорошего качества связи и телевизионной передачи по коаксиальному кабелю отклонение импеданса ΔZ не должно превышать 0,45 Ω, что соответствует коэффициенту отражения
