Степени свободы (механика)

Содержание

В физике степени свободы (DOF) механической системы — это количество независимых параметров, которые определяют ее конфигурацию или состояние. Он важен для анализа систем организма в машиностроении, гражданском строительстве, аэрокосмической технике, робототехнике и других областях.

Грузы в этом центробежном губернаторе имеют две степени свободы, поскольку их положение в пространстве определяется двумя координатами: 1) углом поворота вала; 2) углом отклонения рычагов от вертикали (т.е. от оси вала).

Степени свободы в механике — набор независимых координат перемещения и/или вращения, которые полностью определяют положение системы или тела (а вместе с их временными производными — соответствующими скоростями — полностью определяют состояние механической системы или тела, т.е. ее положение и движение).

В отличие от обычных декартовых или других координат, эти координаты принято называть обобщенными координатами (декартовы, полярные или другие специальные координаты являются частным случаем обобщенных координат). По сути, они представляют собой минимальный набор чисел, которые полностью определяют текущее положение (конфигурацию) данной системы.

Требование, чтобы это множество было минимальным или независимым, означает, что оно подразумевает набор координат, необходимых для описания положения системы только среди возможных движений (например, при рассмотрении математического маятника предполагается, что его длина не может изменяться, и поэтому координата, характеризующая расстояние между грузом и точкой подвеса, не является его степенью свободы, поскольку она не может изменяться — т.е. число степеней свободы математического маятника в пространстве равно 2, а тот же маятник, имеющий m

Если рассматривать систему со связями (точнее, с ограничивающими связями), то число степеней свободы механической системы меньше числа декартовых координат всех материальных точек системы, т.е:

n = 3 N − n l i n k, ,>где n — количество степеней свободы, N — количество материальных точек системы, n link>>- Количество биржевых облигаций, без лишних комм. 1 .

Число степеней свободы зависит не только от природы реальной системы, но и от модели (приближения), в рамках которой изучается система. Даже в рамках классической механики (в которой в целом написана эта статья) число степеней свободы макроскопической системы огромно, если не принимать во внимание другие подходы, упрощающие проблему. Поскольку связи не могут быть абсолютно жесткими (то есть их можно рассматривать как связи только в определенном приближении), фактическое число степеней свободы механической системы можно оценить как минимум в три раза больше, чем число атомов (и бесконечное в приближении континуума). На практике, однако, используются подходы, позволяющие радикально упростить задачу и уменьшить число степеней свободы при рассмотрении системы, так что в практических расчетах число степеней свободы является конечным и обычно довольно малым.

Подход абсолютного твердого тела, который является примером жесткой связи, наложенной на каждую пару материальных точек тела, уменьшает число степеней свободы твердого тела до 6. Следовательно, системы, состоящие из большого числа твердых тел, рассматриваемые с помощью этого подхода, имеют небольшое число степеней свободы, которое может быть уменьшено за счет дополнительных связей (соответствующих соединениям и т.д.). 2 .

Этот чебышевский механизм имеет только одну степень свободы, поскольку его положение полностью определяется углом поворота одного (любого) из трех подвижных элементов — L2, L3 или L4.

Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных.
Автомобиль, если его рассматривать как твёрдое тело, перемещается по плоскости, а точнее говоря, по некоторой двумерной поверхности (в двумерном пространстве). Он имеет две степени свободы (одну вращательную и одну поступательную).
Поезд вынужден перемещаться по рельсовому пути, и поэтому он имеет только одну степень свободы.

Степени свободы в пространстве большей размерности

В общем случае твёрдое тело в пространстве d измерений имеет d + d ( d − 1 ) 2>>степеней свободы ( d поступательных и d ( d − 1 ) 2>>вращающийся).

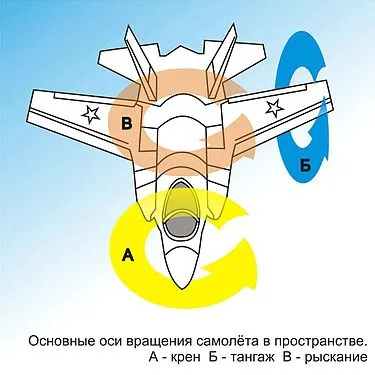
Кинематика самолета: В дополнение к трем поступательным, самолет имеет три вращательные степени свободы (см. рисунок).

Упругие или деформируемые тела можно рассматривать как систему из множества мельчайших частиц (бесконечное число степеней свободы), поэтому систему часто аппроксимируют как имеющую конечное число степеней свободы.

Если основным объектом анализа является движение, которое может вызвать большие смещения, деформированное тело может быть аппроксимировано как полное твердое тело, а иногда даже как материальная точка для упрощения расчетов. Например, если исследуется движение элемента механизма, совершающего большое перемещение, то в первом приближении (и с хорошей точностью) можно рассматривать элемент как абсолютно твердое тело (и, при необходимости, корректировать его малые деформации позже, когда основное движение уже рассчитано). Это особенно актуально при изучении, например, орбиты спутника, и если не учитывать ориентацию спутника, то можно рассматривать его как материальную точку — т.е. ограничиться описанием спутника тремя степенями свободы.

Движение и размерности

В общем случае твердое тело имеет d ( d + 1)/2 степеней свободы в d измерениях (d поступательных и d ( d-1)/2 вращательных).

Упругие или деформируемые тела можно рассматривать как систему многих маленьких частиц (бесконечное число степеней свободы; в этом случае систему часто аппроксимируют как систему с конечным числом степеней свободы.

Если основным объектом анализа является движение, вызывающее большие перемещения (например, движение спутника), то для упрощения расчетов деформированное тело можно аппроксимировать как абсолютно твердое тело.

Системы тел

Система с большим количеством тел может иметь столько степеней свободы в целом, сколько составляет сумма степеней свободы тел, составляющих систему, за вычетом степеней свободы, ограниченных внутренними связями. Механизм с большим количеством связанных тел может иметь большее число степеней свободы, чем одно свободное твердое тело. В данном случае термин «степени свободы» используется для обозначения количества параметров, необходимых для точного определения положения механизма в пространстве.

Особым типом механизма является открытый механизмкинематическая цепьв котором жесткие звенья имеют подвижные шарниры, обеспечивающие одну степень свободы (если это шарнирпетляшарнир или скользящее соединение) или две степени свободы (если это цилиндрическое звено). Цепи этого типа в основном используются вРобототехника,биомеханикаи для космических механизмов.

Человеческая рука имеет 7 степеней свободы.

Робот с механизмом для управления всеми 6физические степени свободыназываетсяв полном одиночестве. Если робот имеет меньше управляемых степеней свободы, его называют неавтономным. Робот или другой объект, имеющий больше управляемых степеней свободы, чем число естественных степеней свободы, называется избыточным.

Определение степеней свободы механизмов

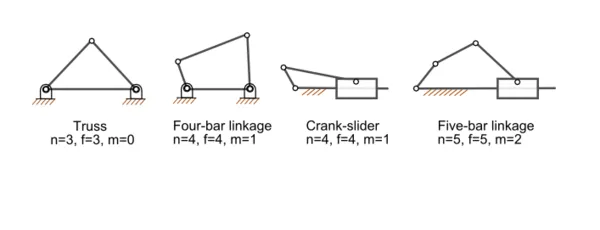
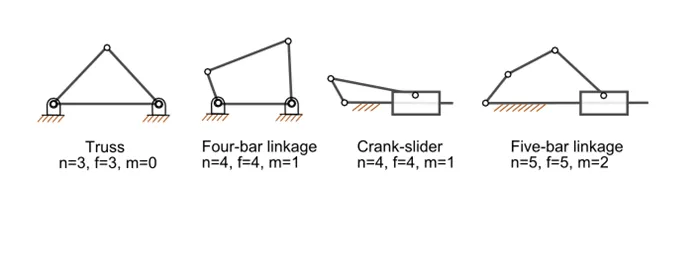
Определение числа степеней свободы плоских механизмов: m — число степеней свободы; n — число звеньев механизма (включая неподвижное звено); f — число подвижных звеньев механизма.

Большинство обычных механизмов имеют одну степень свободы, т.е. есть входное движение, которое определяет выходное движение. Кроме того, большинство механизмов являются плоскостными. Пространственные механизмы более сложны для расчета.

Для расчета степеней свободы механизмаФормула Чебышева — Граблера — Кутцбаха(Для плоских механизмов это проще, чем для плоскостных.).

Для плоских механизмов эта формула может быть сформулирована в простейшем виде:

кинематические парыс одной степенью свободы (петляήнажмитесоединение),

В более общем виде формула Чебышева-Граблера-Кутцбаха для плоских механизмов с более сложными соединениями:

Или для пространственного механизма (механизма с трехмерным движением):

— число степеней свободы,

— количество частей механизма (включая неподвижную часть — основание),

Число степеней свободы — это число независимых величин, которые должны быть заданы, чтобы однозначно определить положение тела в пространстве. Тело имеет шесть степеней свободы, независимо от того, сколько N точек оно содержит.

Rigid bodies edit

Translation and rotation:

Walking (or surging ): Moving forward and backward;
Strafing (or swaying ): Moving left and right;
Elevating (or heaving ): Moving up and down;
Roll rotation : Pivots side to side;
Pitch rotation : Tilts forward and backward;
Yaw rotation : Swivels left and right;

Например, траектория самолета в полете имеет три степени свободы, а его положение вдоль траектории — три степени свободы, итого шесть степеней свободы.

For rolling in flight and ship dynamics, see roll (aviation) and roll (ship motion), respectively.
- An important derivative is the roll rate (or roll velocity), which is the angular speed at which an aircraft can change its roll attitude, and is typically expressed in degrees per second.
- One important derivative is the yaw rate (or yaw velocity), the angular speed of yaw rotation, measured with a yaw rate sensor.
- Another important derivative is the yawing moment, the angular momentum of a yaw rotation, which is important for adverse yaw in aircraft dynamics.
Lower mobility edit

Физические ограничения могут ограничивать количество степеней свободы жесткого тела. Например, блок, скользящий по плоскому столу, имеет 3 DOF 2T1R, состоящие из двух перемещений 2T и одного вращения 1R; робот позиционирования XYZ, такой как SCARA, имеет меньшую подвижность 3 DOF 3T.

Mobility formula edit

Формула подвижности измеряет количество параметров, определяющих конфигурацию набора жестких тел, ограниченных шарнирами, соединяющими эти тела. 3 4 Система из n жестких тел, движущихся в пространстве, имеет 6 n степеней свободы, измеренных относительно неподвижной рамы. Для измерения степеней свободы этой системы неподвижное тело включается в счет тел, чтобы подвижность не зависела от выбора тела, образующего неподвижную раму. Тогда степеней свободы невозмущенной системы N = n + 1 M = 6 n = 6 ( N — 1 ), так как неподвижное тело не имеет степеней свободы относительно самого себя. Суставы, соединяющие тела в этой системе, лишают их степеней свободы и уменьшают подвижность. В частности, шарниры и ползунки накладывают по пять ограничений и, следовательно, отнимают пять степеней свободы. Удобно определить количество ограничений c, накладываемых шарниром, как функцию свободы f шарнира, где c = 6 — f. В случае шарнира или ползуна, которые являются шарнирами с одной степенью свободы, f = 1 и, следовательно, c = 6 — 1 = 5. Отсюда следует, что подвижность системы, состоящей из n подвижных звеньев и j шарниров со свободой f_i, i = 1,. j, is given by M = 6 n − ∑ i = 1 j ( 6 − f i ) = 6 ( N − 1 − j ) + ∑ i = 1 j f i ^\ (6-f_ )=6(N-1-j)+\sum _^\ f_>Следует помнить, что N включает в себя фиксированную связь. Есть два важных особых случая: (i) простая открытая цепь и (ii) простая замкнутая цепь. Простая открытая цепь состоит из n подвижных звеньев, соединенных n шарнирами, один конец которых соединен с заземленным звеном. Поэтому в данном случае N = j + 1 и подвижность цепи равна M = ∑ i = 1 j f i<\displaystyle M=\sum _^\ f_>В простой замкнутой цепи n подвижных звеньев с n + 1 шарнирами нанизаны друг на друга так, что оба конца соединены с базовым звеном и образуют петлю. В этом случае N = j и подвижность цепи равна M = ∑ i = 1 j f i — 6.<\displaystyle M=\sum _^\ f_ -6>Примером простой разомкнутой цепи является серийный робот-манипулятор. Эти роботизированные системы состоят из ряда звеньев, соединенных шестью шарнирными или призматическими соединениями с одной степенью свободы, так что система имеет шесть степеней свободы. Примером простой замкнутой цепи является пространственное соединение четырех стержней RSSR. Сумма степеней свободы этих звеньев равна восьми, так что подвижность звена равна двум, причем одна из степеней свободы — это поворот звена вокруг линии, соединяющей два звена S.

Planar and spherical movement edit

Примером плоской, простой, замкнутой цепи является плоская четырехзвенка, которая представляет собой четырехзвенную петлю с четырьмя шарнирами одной степени свободы и поэтому имеет подвижность M = 1.

Systems of bodies edit

Система из нескольких тел имеет комбинированную DOF, равную сумме DOF тел, за вычетом внутренних ограничений, которые применяются к относительному движению. Механизм или связь, состоящая из нескольких жестких тел, соединенных вместе, может иметь больше степеней свободы, чем степени свободы одного жесткого тела. Здесь термин «степени свободы» используется для описания количества параметров, необходимых для определения пространственного положения связи. Оно также определяется в контексте конфигурационного пространства робота, рабочего пространства и рабочей зоны.

Electrical engineering edit

В электротехнике термин степень свободы часто используется для описания количества направлений, в которых фазированная антенная решетка может формировать либо лучи, либо нули. Оно на единицу меньше числа элементов, содержащихся в решетке, поскольку один элемент используется в качестве опорной точки, относительно которой может быть применена конструктивная или деструктивная интерференция с любым из других элементов антенны. радарной практике и практике линий связи, причем управление лучом больше используется в радарных приложениях, а зануляющее управление — для подавления помех в линиях связи.
- Gimbal lock – Loss of one degree of freedom in a three-dimensional, three-gimbal mechanism
- Kinematics – Branch of physics describing the motion of objects without considering forces
- Kinematic pair – Connection between two physical objects which constrains their relative movement
- XR-2 – Educational robot
Примеры

Дисперсия s 2 определяется как средний квадрат выборочных дисперсий (или остатков) n выборок данных:

s 2 = ( p — p ) / (n-1)

Где p — вектор несоответствий p = (x1 -, x2 -, …., Xn — ), а толстая точка ( — ) — оператор скалярного произведения. Альтернативно, формула дисперсии может быть записана следующим образом:

В любом случае, обратите внимание, что при вычислении среднего квадратического остатка он делится не на n, а на (n-1), поскольку число степеней свободы вектора p равно (n-1), как объяснялось в предыдущем разделе.

Если при вычислении дисперсии делить на n, а не на (n-1), то результат будет иметь смещение, что очень важно для значений n до 50.

В литературе также можно встретить формулу дисперсии с делителем n вместо (n-1), когда речь идет о дисперсии популяции.

Но набор случайной величины остатков, представленный вектором р, Хотя он имеет размерность n, он имеет только (n-1) степеней свободы. Однако, если количество данных достаточно велико (n>500), обе формулы сходятся к одному результату.

Калькуляторы и электронные таблицы предоставляют обе версии дисперсии и стандартного отклонения (которое является квадратным корнем из дисперсии).

Исходя из представленного здесь анализа, мы рекомендуем всегда выбирать версию с (n-1) при расчете дисперсии или стандартного отклонения, чтобы избежать искажения результатов.

В распределении хи-квадрат

Некоторые распределения вероятностей для непрерывной случайной величины зависят от параметра, называемого степенью свободы — так обстоит дело с распределением хи-квадрат (χ 2 ).

Название этого параметра происходит именно от степеней свободы базового случайного вектора, к которому применяется данное распределение.

Предположим, что у нас есть g популяций, из которых мы берем выборки размером n:

Популяция j, среднее и стандартное отклонение которой Sj, соответствует нормальному распределению N (, Sj ).

Стандартизированная или нормализованная переменная zj_яопределяется как:

А вектор zj определяется как:

Zj = (zj₁, zj₂, …, Zj_я, …, Zj_п) и соответствует стандартному нормальному распределению N (0,1).

Следуйте распределению χ 2 (g), называемому распределением хи-квадрат со степенями свободы грамм.

При проверке гипотез (с проработанным примером)

Если вы хотите проверить гипотезу на основе определенного набора случайных данных, вам необходимо знать число степеней свободы g, прежде чем применять тест хи-квадрат.

Например, мы проанализируем собранные данные о предпочтениях мужчин и женщин в отношении шоколадного или клубничного мороженого в конкретном кафе-мороженом. Частота, с которой мужчины и женщины выбирают клубнику или шоколад, показана на рисунке 2.

Сначала рассчитывается таблица ожидаемых частот путем умножения общего количества строк на общее количество столбцов, разделенных на набор данных. Результат показан на следующем рисунке:

Затем вычисляем хи-квадрат (по данным) по следующей формуле:

Где F_ή— являются наблюдаемыми частотами (рисунок 2), а F_и— Суммирование производится по всем строкам и столбцам, что в нашем примере дает четыре члена.

После выполнения операций вы получите:

Теперь мы должны сравнить с теоретическим хи-квадратом, который зависит от числа степеней свободы g.

В нашем случае это число определяется следующим образом:

g = (количество строк — 1) (количество столбцов — 1) = (2 — 1) (2 — 1) = 1 * 1 = 1.

Оказывается, что число степеней свободы g в этом примере равно 1.

Если вы хотите проверить или отвергнуть нулевую гипотезу (H0: нет корреляции между TEST и GOLD) с уровнем значимости 1 %, теоретическое значение хи-квадрат рассчитывается со степенью свободы g = 1.

Мы ищем значение, при котором кумулятивная частота равна (1 — 0,01) = 0,99, т.е. 99 %. Это значение (которое можно взять из таблиц) равно 6 636.

Если теоретический chi превышает расчетный chi, проверяется нулевая гипотеза.

То есть, с помощью собранных данных.Наблюдение не ведетсякорреляция между переменными VKU и GENDER.

Определение степеней свободы механизмов править | править код

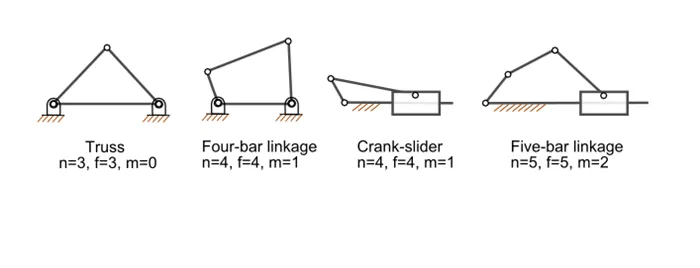
Определение числа степеней свободы плоских механизмов: m — число степеней свободы; n — число звеньев механизма (включая неподвижное звено); f — число подвижных звеньев механизма.

Большинство обычных механизмов имеют одну степень свободы, т.е. есть входное движение, которое определяет выходное движение. Кроме того, большинство механизмов являются плоскими. Пространственные механизмы рассчитать сложнее.

Для расчета степеней свободы механизмов используется формула Чебышева-Граблера-Кутцбаха.

Для плоских механизмов эта формула может быть сформулирована в простейшем виде:

m = 3 ( n — 1 ) — 2 f, где m — число степеней свободы, n — число звеньев механизма (включая одно неподвижное звено — основание) и f — число кинематических пар с одной степенью свободы (петля или скользящее звено).

Формула Чебышева-Граблера-Кутцбаха является более общей для плоских механизмов с более сложными соединениями звеньев:

Простые механизмы способны к сложным движениям

Или для пространственного механизма (механизма с трехмерным движением):

m = 6 ( n − j − 1 ) + ∑ i = 1 j f i, ^\ f_,>где m — количество степеней свободы; n — количество звеньев механизма (включая одно неподвижное звено — основание); j — общее количество подвижных соединений звеньев, не рассматривая количество степеней свободы этих соединений; ∑ i = 1 j f i ^\ f_>- Сумма всех степеней свободы всех подвижных суставов (шарниров).

Гидропривод править | править код

Число степеней свободы гидравлической системы можно определить простым подсчетом независимо управляемых гидромоторов.

В электротехнике понятие степеней свободы часто используется для описания количества направлений, в которых группа фазированных антенных решеток может проецировать свои лучи. Оно на единицу меньше количества элементов, содержащихся в массиве.

Принцип возможных перемещений править | править код

В теоретической механике хорошо известен принцип возможных перемещений, который, как и уравнения равновесия статики, может быть использован для определения эффектов внешних сил, действующих на механическую систему. Число уравнений, вытекающих из принципа возможных перемещений, равно числу степеней свободы данной механической системы.

Эта формула важна, например, для расчета двигателей внутреннего сгорания.

Степени свободы (механика) — Degrees of freedom (mechanics). Степени свободы в механике.