Мы хотим узнать, почему при замедлении ускорение отрицательное. Например, лодка снизилась с 9 м/с до 7 м/с за первую секунду, до 5 м/с за вторую секунду и до 3 м/с за третью секунду. Скорость изменяется на «-2 м/с». 3-5=-2, 5-7=-2, 7-9=-2 м/с. Именно отсюда берется отрицательное значение ускорения.
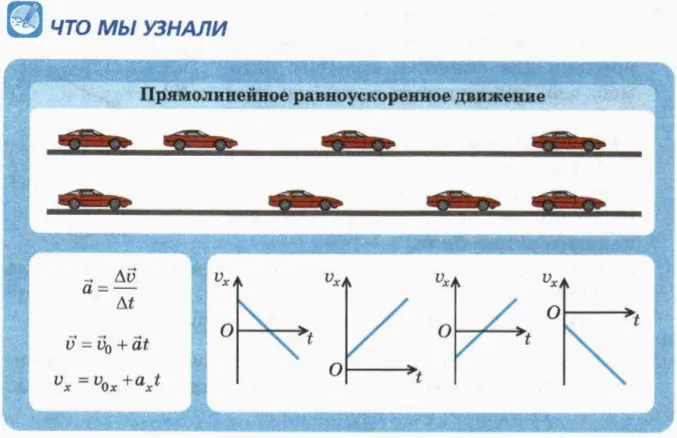
Прямолинейное равноускоренное движение графики на примере
Диаграммы линейного, равномерно ускоренного, линейного движения — это графическое представление хода материальных сред, где физические величины выражаются в виде функций.
Они могут показать зависимость от времени различных путей, скоростей или ускорений. При изоускоренном движении ускорение данного механизма остается неизменным независимо от промежутка времени.
Определение
Если рассматривать путь движения как прямую линию, то линейное движение с одинаковым ускорением вдоль этой линии — это движение материальной точки с постоянным изменением скорости во времени и одинаковым ускорением.
Прежде чем перейти к формулам, необходимо уточнить, что в равномерно ускоренное линейное движение вовлечены физические процессы
-
Постоянство величины ускорения с течением времени,

Это один из способов представления движения на бумаге.
На диаграмме ускорение материала зависит от его движения за определенный промежуток времени и имеет значение: a=const.
Структура диаграммы такова: горизонтальная линия — ось абсцисс, здесь масштабируется время, вертикальная линия — ордината, где отмечается, с каким ускорением движется объект.
Читайте также: Что такое подготовительная сессия для студентов-заочников: характеристика, время и продолжительность.
В этом случае график отражает, как ускорение зависит от периода времени. В этом случае равномерное линейное движение совпадает с временной шкалой, так как ускорение в этом случае равно «0».
Графическое представление движения точки с равным ускорением также выделено прямой линией, но параллельной линии времени. Существуют различия между возрастающим или убывающим ускорением, расположенным на верхнем или нижнем конце оси времени.
Диаграмма скоростей показывает и определяет движение механизмов в определенный момент времени, зависимость движения от него, включая события:
- Нахождение предмета в нужное для определения время.
- Весь пройденный путь за временной промежуток.
- Период, за который тело переместилось на расстояние.
- Самые длинные или короткие точки между предметами, пройденную траекторию в любой требуемый час.
- Встречу двух инструментов передвижения в определенный момент.
Событие может быть описано графически, если от него зависит время:
- скорость;
- ускорение;
- местонахождение тела.
Необходимо знать разницу между координатами, в которых находится объект, и линией траектории, по которой он двигался в каждой точке.
Ученые прибегают к графическим представлениям, чтобы более четко выразить кинематику движений.
Как графически решить задачу
В задаче ставится условие определить зависимость от величины Ax(t), выраженной на графике.
Необходимо определить Vx(t), где тело в начале пути движется со скоростью «0», т.е. t = 0.
Решение состоит из точек:
- Так как равноускоренное движение, в котором материальный предмет меняет свою скорость по формуле vx(t)=v0x+axt, где v0x=0, тогда формула преобразится: vx(t)=v0x+axt.
- Первый участок показывает 0≤ t
- Второе значение представляет 1≤ t<3, с ускорением ax=-1мc2, v=(t)=-t и графиком.
Читайте также: Различные подходы к классификации методов обучения, мотивации и стимулирования.
При построении любой графической системы следует помнить, что направление вектора меняется с размером материала по мере его перемещения.
a=(Vк-Vн)/t
Пока тело движется, ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, а затем начал ускоряться в гору. Какова будет его скорость через 10 секунд, если ускорение равно 0,5 м/с? Решение. Vn=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд. Итак: Vn= 6 + 0,5 — 10 = 11 м/с. Ответ: Кирилл разгонится до 11 м/с.
Формула расстояния при равноускоренном движении
S = t* (Vн+ Vк)/2
Где: S — расстояние, пройденное за время t, Vn — начальная скорость, Vk — конечная скорость, a — ускорение тела, t — время.
Для равномерно ускоренного движения с неизвестным временем пробега, но заданными начальной и конечной скоростями, пройденное расстояние можно определить по следующей формуле:
2аS = Vк2-Vн2
где S — расстояние, пройденное за время t, V0 — начальная скорость, V — скорость в момент времени t и a — ускорение тела.
Задача 2
Водитель такси получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость составляет 15 м/с? Решение. Поскольку таксист начал движение, начальная скорость равна нулю (Vn=0), Vk=15м/с, ускорение a=0,1м/с2. Мы получаем: На расстоянии 1 125 м от начала движения скорость такси равна 15 м/с.
Перемещение при равноускоренном движении
Важно помнить о разнице между движением и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путешественник прошел расстояние S1 в одном направлении и S2 в противоположном, то перемещение тела составляет S1 + S2, а перемещение S1 — S2. В некоторых задачах путь и смещение могут совпадать, но не всегда.
Как найти ускорение тела по графику?
График ускорения — это графическое представление уравнения ускорения тела a = a(t). График a(t) используется для описания движения тела. Этот график представляет движение с одинаковым ускорением. Здесь вы можете увидеть, как будут выглядеть созданные вами графики.
Следующий набор диаграмм относится к случаю, когда тело движется с возрастающей скоростью вдоль оси Ox (рис. 4), т.е. это равномерно ускоренное движение.
Рисунок 4. Тело, движущееся с равномерным ускорением — рис. а) — в направлении оси ox. Изменение координаты от времени x(t) описывается правой частью параболы — см. рис. b), график v(t) скорости представлен наклонной линией — см. рис. c), а график постоянного ускорения a(t) — см. рис. d) представлен горизонтальной линией, лежащей выше оси времени.
Теперь координата x изменяется по квадратичному закону вместо линейного. На графике квадратичное изменение выглядит как ветвь параболы (рис. 4b). Тело движется вдоль оси, и его скорость увеличивается. Это движение описывается правой ветвью параболы, направленной вверх.
Уравнение, описывающее квадратичное изменение координат, имеет следующий вид:
Скорость также увеличивается (Рисунок 4c). Увеличение скорости описывается нисходящей прямой линией — т.е. линейной зависимостью:
\ v = v_ + a \cdot t \.
Ускорение присутствует (Рисунок 4d) и не изменяется:
Скорость и ускорение имеют общее направление с осью волы, поэтому их проекции на ось положительны и их графики лежат выше оси времени.
Примечания:
1). 1:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон является уравнением первого порядка, а график — наклонной прямой линией.
3). Квадратичный закон — это уравнение второй степени, график — парабола.
4) Если скорость увеличивается, то для графика координат x(t) выбираем правую ножку параболы, а если скорость уменьшается, то левую.
Равноускоренное движение против оси
Если тело увеличивает свою скорость, двигаясь в направлении, противоположном оси (рис. 5a), то ветвь параболы, описывающая изменение координат тела, идет вниз (рис. 5b).
Скорость направлена вдоль оси и увеличивается в отрицательном диапазоне. Это изменение скорости представлено прямой линией, направленной вниз (рис. 5c).
Рисунок 5. Тело движется изотропно и колеблется относительно оси Ox — рисунок a). Координата изменяется параболически — рисунок b), бифуркация уходит вправо по мере увеличения скорости. Скорость — рисунок c) — и ускорение — рисунок d) — направлены к оси Ox, их графики лежат ниже оси времени.
Примечание: Чтобы увеличить скорость (по модулю), векторы скорости и ускорения должны быть конгруэнтны (связь).
С увеличением скорости векторы скорости и ускорения сходятся. В то же время, однако, они лежат против оси, так что проекции векторов \(\vec\) и \(\vec\) на ось Ox отрицательны. Поэтому графики скорости и ускорения лежат ниже горизонтальной оси времени.
Ускорение (рис. 5d) остается неизменным и поэтому представлено горизонтальной линией. Однако эта линия лежит ниже горизонтальной оси времени, поскольку ускорение имеет отрицательную проекцию на ось волы.
Как составить уравнение скорости по графику?
График скорости График скорости — это графическое представление уравнения для скорости тела v = v(t). График v(t) используется для описания движения тела. Этот график представляет движение с одинаковым ускорением.
Когда объект удаляется от целевой точки вдоль отрицательной оси, смещение объекта вдоль отрицательной оси Y принимается отрицательным. Если положение объекта отклоняется от направления его движения, то предполагается, что перемещение объекта происходит в отрицательном направлении.
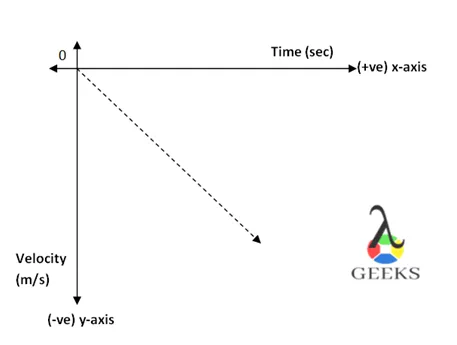
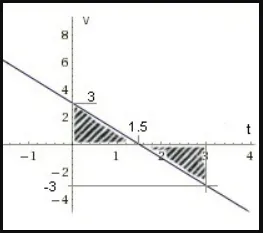
Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость уменьшается со временем, наклон графика отрицательный, поэтому ускорение также отрицательное.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение не меняется со временем, оно имеет постоянное значение, кривая a(t) — прямая линия, параллельная оси времени.
При равномерном движении путь изменяется в соответствии с линейной зависимостью от. В координатах. Диаграмма представляет собой наклонную линию.
Для начальной координаты тела, скорости, действует зависимость
Если тело движется в противоположном направлении, скорость отрицательна, а начальная координата одинакова, то зависимость имеет вид
Правило для определения пути по графу v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило для определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляется, то ускорение отрицательное, угол графика тупой, поэтому находим тангенс прилежащего угла.
Зависимость расстояния от времени. При изобарическом движении путь изменяется в соответствии с квадратичной зависимостью. В координатах зависимость имеет вид. График представляет собой ветвь параболы.
График движения в. График движения в .
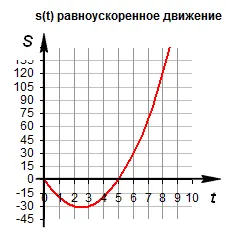
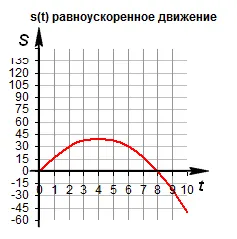
График движения в. График движения в .
Механика
График механического движения. Выражайте взаимосвязь между физическими величинами с помощью функций. Функции называются
Зависимость ускорения от времени: Поскольку для равномерного движения ускорение равно нулю, зависимость a(t) представляет собой прямую линию на оси времени.
Зависимость скорости от времени. Скорость не меняется со временем, график v(t) представляет собой прямую линию, параллельную оси времени.
Правило для определения перемещения по графику v(t): Численное значение смещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость смещения от времени. График s(t) является наклонной прямой.
Правило для определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Зависимость ускорения от времени. Ускорение не меняется со временем, оно имеет постоянное значение, кривая a(t) — прямая линия, параллельная оси времени.
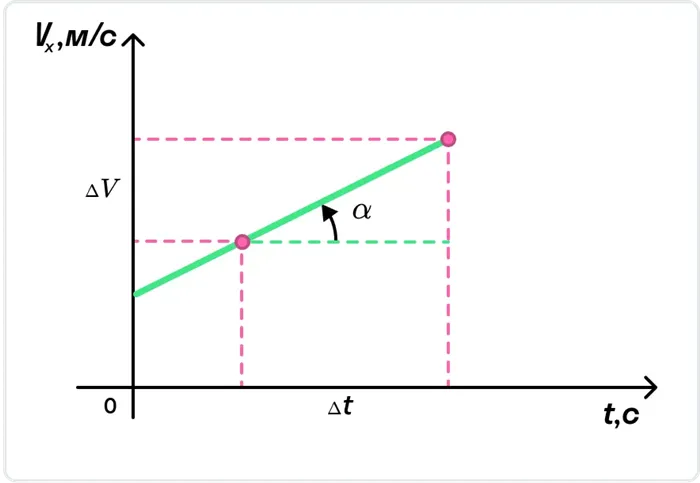
При равномерном движении путь изменяется в соответствии с линейной зависимостью от. В координатах. Диаграмма представляет собой наклонную линию.
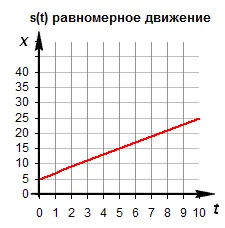
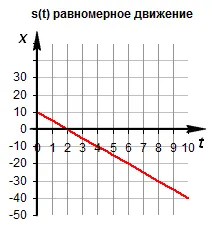
| Для начальной координаты тела, скорости, действует зависимость | Если тело движется в противоположном направлении, скорость отрицательна, а начальная координата одинакова, то зависимость имеет вид |
Правило для определения пути по графу v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило для определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляется, то ускорение отрицательное, угол графика тупой, поэтому находим тангенс прилежащего угла.
Зависимость расстояния от времени. При изобарическом движении путь изменяется в соответствии с квадратичной зависимостью. В координатах зависимость имеет вид. График представляет собой ветвь параболы.
- График движения в. График движения в .
- График движения в. График движения в .
Равноускоренное движение: формулы и примеры
Что такое равноускоренное движение?
В физике равномерно ускоренное движение — это движение, при котором вектор ускорения не изменяется ни по величине, ни по направлению.
Проще говоря, равномерно ускоренное движение — это неравномерное движение (т.е. движение с разными скоростями), ускорение которого постоянно в течение определенного периода времени.
Представьте, что автомобиль начинает движение, в первые 2 секунды его скорость составляет 10 м/с, в следующие 2 секунды он движется со скоростью 20 м/с, а еще через 2 секунды он уже движется со скоростью 30 м/с. Это означает, что каждые 2 секунды он ускоряется на 10 м/с, это движение изо-ускоренное.
Читайте также: Источники света — пособие для студентов
Отсюда можно вывести очень простое определение равномерного ускорения: Это движение любого физического тела, при котором его скорость изменяется равномерно в течение равных промежутков времени.
Примеры равноускоренного движения
Хорошим примером равномерно ускоренного движения в повседневной жизни может служить велосипед, едущий вниз по склону (но не велосипед, на котором едет велосипедист), или камень, брошенный под определенным углом к горизонту.
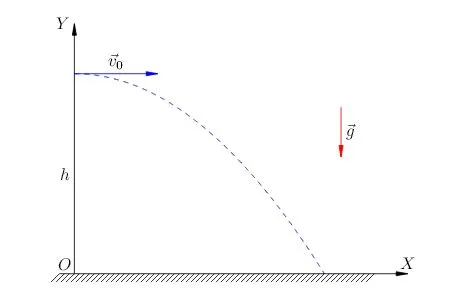
Кстати, пример камня можно рассмотреть более внимательно. В каждой точке траектории на камень действует ускорение свободного падения g. Ускорение g не меняется, т.е. остается постоянным и всегда направлено в одну сторону (это основное условие равномерного движения).
Полезно представить полет брошенного камня как сумму перемещений вдоль вертикальной и горизонтальной осей системы координат.
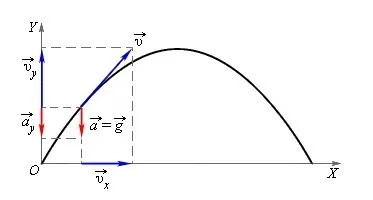
Если движение камня вдоль оси x равномерно и прямолинейно, то вдоль оси y оно равномерно ускорено и прямолинейно.
Формула равноускоренного движения
- Формула скорости при равноускоренном движении будет иметь такой вид:
- V = V0 + at
- Где V0 – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.
- При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.
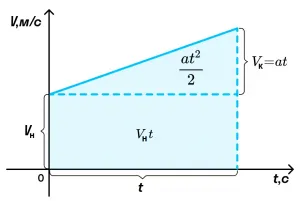
Ускорение можно определить по наклону графика скорости. На этом рисунке он равен отношению сторон треугольника ABC.
Чем больше угол b, тем больше наклон и, следовательно, наклон кривой по отношению к оси времени и тем больше ускорение тела.
Рекомендуемая литература по теме
- Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 37. — 560 с. — ISBN 5-9221-0225-7.
Изучение законов ускорения
Изучение законов ускорения
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ. Поступательное движение тела — это движение, при котором каждая прямая, жестко связанная с движущимся телом, остается параллельной самой себе. Положение тела (материальной точки) в декартовой системе координат характеризуется радиус-вектором или тремя его проекциями (X, Y, Z) на координатную ось (рис. 1). Когда тело движется, его положение меняется со временем. Рисунок 1. Зависимость его радиуса, вектора или проекций от времени называется кинематическим уравнением движения. или X=X(t); Y=Y(t); Z=Z(t) Величина, характеризующая изменение радиус-вектора (также называемого вектором движения) в единицу времени, называется вектором скорости. Вектор мгновенной скорости (или скорость в определенный момент времени) определяется выражением: ; или ; ; ; ; ; ; ;, где Vx, Vy, Vz — проекции вектора скорости на координатные оси. Вектор средней скорости совпадает с вектором перемещения, а вектор мгновенной скорости направлен по касательной к траектории движения. Когда тело движется, его скорость может меняться как по величине, так и по направлению. Величина, описывающая изменение вектора скорости в единицу времени, называется вектором ускорения. Вектор мгновенного ускорения определяется выражением: или ; ; ; ; ; ; ; .
Поскольку при криволинейном движении скорость может меняться как по величине, так и по направлению, вектор полного ускорения имеет две составляющие: нормальное ускорение (также называемое центростремительным) и тангенциальное ускорение (также называемое касательным) (рис. 2):
(1) Нормальное ускорение описывает скорость изменения скорости относительно направления. Она направлена вдоль перпендикуляра к касательной в данной точке траектории. Мера этого ускорения определяется выражением (2), где V — мгновенная скорость, а R — радиус кривизны траектории в рассматриваемой точке. Тангенциальное ускорение характеризует скорость движения по модулю.
В этой точке она является касательной к траектории движения. Мера этого ускорения определяется выражением.
(3) При классификации механических движений тел в соответствии с двумя точками зрения — по типу изменения скорости и по форме траектории — существует четыре типа движения: 1) равномерное прямолинейное движение: (траектория — прямая линия); 2) неравномерное прямолинейное: (траектория — прямая линия); 3) равномерное прямолинейное: (траектория — кривая); 4) неравномерное прямолинейное: (траектория — кривая). Частным случаем неравномерного прямолинейного движения является ускоренное движение — движение тела с постоянным ускорением. Законы этого движения можно вывести из второго закона Ньютона.
Материальная точка массой m должна двигаться вдоль оси S с постоянным ускорением α (равновесное ускорение). Поскольку ускорение постоянно, сила, действующая на точку, также постоянна.
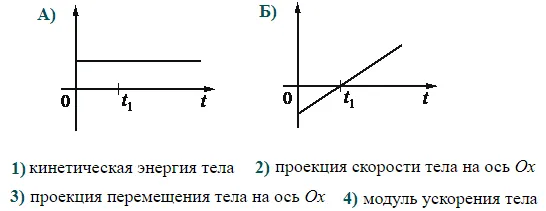
1) Средняя и мгновенная скорость. 2) Среднее и мгновенное ускорение. 3) Нормальное и тангенциальное ускорение. 4) Законы Ньютона. 5) Равномерно ускоренное движение. Вывод законов движения и скорости.
6) Методы регулировки и измерения.
Ускорение
Определение прямолинейного равномерно ускоренного движения относится к изменению скорости. Как определяется изменение скорости?
Если мы определим его как 0скорость тела в начальный момент времени и
Мы также можем переписать эту формулу следующим образом

На рисунке 5.3 показано, как вычислить вектор скорости D
? 1 Какой из рисунков 5.3 (a или b) соответствует увеличению скорости, а какой — уменьшению?
Теперь мы хотим ввести понятие ускорения.
Ускорение в интервале времени Δt, в котором произошло изменение: (Здесь мы должны говорить о мгновенном ускорении, которое определяется в достаточно короткие промежутки времени — аналогично тому, как мы определяли мгновенную скорость выше. В случае прямолинейного равномерно ускоренного движения мгновенное ускорение постоянно).
Как следует из этого определения, ускорение — это векторная величина. Она описывает скорость изменения скорости. Единицей ускорения в СИ является 1 м/с 2 (читается: «метры в секунду за секунду» или «метры, деленные на секунду в квадрате»). Когда тело движется в одном направлении с таким ускорением по модулю, его скорость увеличивается (или уменьшается!) на 1 м/с в секунду.
Когда тело падает, оно движется с ускорением около 10 м/с 2 (если пренебречь сопротивлением воздуха).
Рассмотрим теперь, при каком условии скорость тела увеличивается, а при каком – уменьшается. Из определения (3) следует, что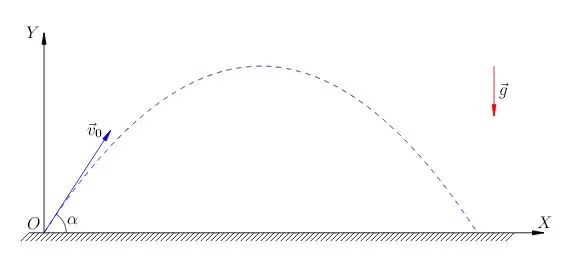 На рисунке 5.4 мы заменили (по сравнению с рисунком 5.3) Δ Δt.
На рисунке 5.4 мы заменили (по сравнению с рисунком 5.3) Δ Δt.
Теперь мы видим, что скорость тела увеличивается, если ускорение направлено в ту же сторону, что и начальная скорость (рис. 5.4, а). Если ускорение противоположно скорости (рис. 5.4, б), то скорость тела уменьшается.
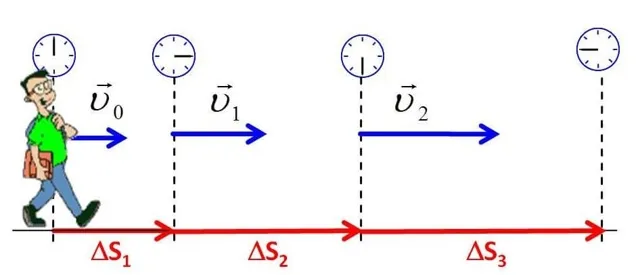
? 2. На каком из рисунков 5.2 (a или b) ускорение автомобиля направлено влево?
Если мы выберем начальное время t0= 0, тогда Δt = t — t0= t — 0 = t. Поскольку Δ — 0из формулы (4) следует, что ось x проходит вдоль траектории движения тела. Затем
Здесь vx— проекция скорости на момент времени t, v0x— проекция начальной скорости, ax— это проекция ускорения.
В формуле (6) проекция начальной скорости v0xи проекция ускорения axможет быть положительным или отрицательным. В зависимости от соотношения между v0xи ax, мера скорости тела, увеличивается или уменьшается со временем.
? 3. четыре автомобиля движутся вдоль оси x. Для некоторого времени зависимость vx(t) для них (в единицах СИ) выражается следующими формулами: 1) vx= 8 + 2t; 2) vx= 20 — 4t; 3) vx= -10 + t- 4) vx= -15 — 3t. (a) Какова проекция начальной скорости и ускорения каждого автомобиля? (b) Какие автомобили ускоряются, а какие замедляются? (c) Какой автомобиль имеет наибольшую скорость по модулю в момент времени t = 2 с; является ли он наименьшим?
При выполнении этого задания вы заметите, что скорость тела увеличивается по модулю, если проекция начальной скорости и проекция ускорения имеют одинаковый знак (обе положительные или обе отрицательные).
График зависимости скорости от времени
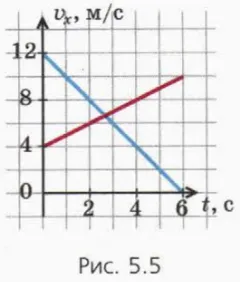
Из формулы (6) следует, что для прямолинейного равномерно ускоренного движения проекция скорости vx линейно зависит от времени t.x(t) является прямой линией.
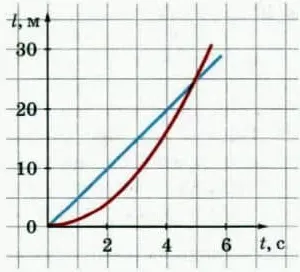
На рисунке 5.5 показана проекция скорости на время для синего и красного автомобилей, движущихся вдоль оси x. a) Какой автомобиль тормозит? Каков его показатель ускорения? б) У какого автомобиля показатель ускорения меньше? Что это значит? c) Напишите зависимость vx(t) для каждого автомобиля. d) Используя эту нотацию, найдите время, через которое скорости автомобилей сравняются. e) Найдите время, через которое скорости автомобилей сравняются. Сверьте свой ответ с приведенными выше диаграммами.
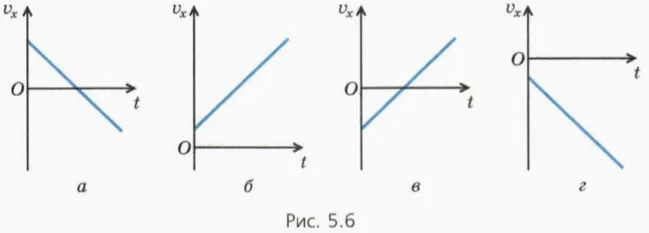
? На рисунке 5.6 показаны графики проекции скорости на время для тел, движущихся вдоль оси x. a) Какие графики описывают движение тела, скорость которого возрастает по модулю во все времена? b) На каких графиках v0x и ax имеют разные знаки? c) Какие графики описывают случаи, когда направление скорости тела меняется на противоположное? d) Постройте графики зависимости коэффициента скорости от времени для всех приведенных случаев.
? 6. проекция скорости во времени для первого тела выражается в единицах СИ по формуле: v12= 6 — t, а для второго тела формула v2x= 2 + t. (a) Нарисуйте vx(t) для каждого тела. (b) В какие моменты времени скорости тел равны (по модулю и направлению)? (c) В какие моменты времени скорости тел равны по модулю?
Дополнительные вопросы и задания
Поезд отходит от платформы в восточном направлении. В это же время на соседней платформе тормозит поезд западного направления. Сделайте схематический рисунок, показывающий направления скорости и ускорения каждого поезда. 8.
8. в каком направлении разгоняется лифт, когда: a) он стартует с первого этажа; b) он тормозит на верхнем этаже? c) он тормозит на третьем этаже и движется вниз? d) он начинает движение на третьем этаже и движется вверх? Воспринимайте движение подъемника как ускорение, а торможение — как то же самое ускорение.
9. автомобиль вылетает из точки в северном направлении и развивает скорость 72 км/ч за 40 с. Представьте движение автомобиля как прямолинейное равномерно ускоренное движение. a) В каком направлении ускоряется автомобиль? b) Каково ускорение автомобиля по модулю? c) Нарисуйте проекцию скорости автомобиля на время. d) Какова была скорость автомобиля через 10 секунд после взлета?








