В заключение темы давайте вспомним некоторые важные физические величины, которые описывают криволинейные движения. В первую очередь, конечно, это время революции. Время оборота — это время, которое требуется телу, чтобы совершить один полный оборот.
Равномерное движение по окружности.
Темы кодировщика USE.
Равномерное круговое движение — это довольно простой пример движения с вектором ускорения, зависящим от времени.
Рассмотрим точку, движущуюся по окружности радиуса. Скорость точки постоянна по модулю и равна. Эта скорость называется линейной скоростью точки.
Период итерации — это время одной полной итерации. Существует очевидная формула для этого периода:
Частота обращения равна обратной величине периода:
Частота показывает, сколько полных оборотов точка совершает в секунду. Частота измеряется в об/с (оборотах в секунду).
Это означает, что точка совершает один полный оборот. Тогда частота равна: об/с; за одну секунду точка совершает 10 полных оборотов.
Угловая скорость.
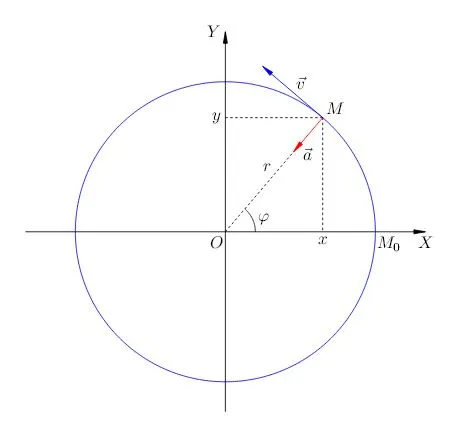
Рассмотрим равномерный поворот точки в декартовой системе координат. Поместим начало координат в центр окружности (рис. 1).
 |
| Рисунок 1. равномерное движение по окружности |
Начальное положение точки, т.е. когда точка имеет координаты. Точка может поворачиваться на угол с течением времени и перемещаться в соответствии с .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
Угол обычно измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол. Поэтому
Если мы объединим формулы (1) и (3), то получим зависимость между линейной скоростью и угловой скоростью:
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно определить путем двойного дифференцирования соотношений (5):
Из формул (5) получаем:
Полученные формулы (6) можно записать в терминах векторного равенства:
Где — радиус-вектор точки поворота.
Мы видим, что вектор ускорения направлен в сторону, противоположную радиус-вектору, то есть к центру окружности (см. рисунок 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным ускорением.
Кроме того, формула (7) дает выражение для меры центростремительного ускорения:
Выразим угловую скорость из (4)
и подставьте его в (8). Получаем еще одну формулу для центростремительного ускорения:
Равномерное движение тела по окружности
1. круговое движение — это движение объекта, траектория которого представляет собой круг. Кончик стрелки часов, кончик лопасти вращающейся турбины, вращающийся вал двигателя и т.д. движутся по кругу.
Когда мы движемся по кругу, направление скорости постоянно меняется. Мера скорости тела может изменяться или оставаться неизменной. Движение, при котором изменяется только направление скорости, а ее мера остается постоянной, называется равномерным круговым движением тела. Под телом в данном случае понимается материальная точка.
Круговое движение объекта характеризуется определенными величинами. К ним относятся, прежде всего, период и частота вращения. Период вращения тела по окружности — это \( T \), время, за которое тело совершает полный оборот. Единица периода равна \( T\,T\, \) = 1 с.
Частота вращения \( (n)\) — это количество полных оборотов тела за одну секунду. Единицей частоты вращения является \( \(,n\, \) = 1 с-1 = 1 Гц (Герц). Один герц — это частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и продолжительностью движения выражается формулой: \( n=1/T \).
Рассмотрим тело, движущееся по круговой траектории и перемещающееся из точки A в точку B за время \( t \). Радиус, соединяющий центр окружности с точкой A, называется радиус-вектором. Когда тело перемещается из точки A в точку B, радиус-вектор поворачивается на угол \( \varphi \) .

Угловая и линейная скорость тела характеризуется его частотой вращения.
Угловая скорость \(\omega \) — это физическая величина, которая соответствует отношению между углом поворота \(\varphi \) радиус-вектора и промежутком времени, за который произошло вращение. Единицей угловой скорости является радиус в секунду, т.е. \( \,\omega\, \) = 1 рад/с. За время, равное продолжительности вращения, угол поворота радиус-вектора равен \( 2\pi \). Поэтому: \( \omega = 2\pi/T\) .
Линейная скорость тела \(v\) — это скорость, с которой тело движется по траектории. Линейная скорость при равномерном круговом движении постоянна по модулю, изменяется по направлению и направлена вдоль касательной к траектории.
Линейная скорость равна отношению между расстоянием, пройденным телом по траектории, и временем, необходимым для прохождения этого расстояния: \( \vec=l/t \). Поэтому: \( \vec=2\pi\!R/T\). Связь между линейной скоростью и угловой скоростью выражается следующей формулой.
Это уравнение утверждает, что чем дальше вращающееся тело находится от центра окружности, тем больше его линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: \( \vec=\frac>\) и направлен в ту же сторону, что и вектор скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по круговой траектории — это физическая величина, которая соответствует отношению квадрата линейной скорости к радиусу круговой траектории. Так как \( v=\omega R\), то \( a=\omega^2R\) .
ПРИМЕРЫ ЗАДАНИЙ
1. в равномерном движении тела по круговой траектории
1) меняется только мера скорости 2) меняется только направление скорости 3) меняется и мера скорости, и направление 4) не меняется ни мера скорости, ни направление.
2 Линейная скорость точки 1 на расстоянии \( R_1 \) от центра вращающегося колеса равна \( v_1 \). Какова скорость \( v_2 \) точки 2, которая находится на расстоянии \( R_2=4R_1 \) от центра?
1) \( v_2=v_1 \) 2) \( v_2=2v_1 \) 3) \( v_2=0,25v_1 \) 4) \( v_2=4v_1 \)
3) Орбитальный период точки на окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv\) 2) \( T=2\pi\!R/v\) 3) \( T=2\pi\pi v\) 4) \( T=2\pi\/v\)
4) Угловая скорость колеса автомобиля рассчитывается по следующей формуле:
1) \(\omega=a^2R\) 2) \(\omega=vR^2\) 3) \(\omega=vR\) 4) (\omega=v/R\)
5) Угловая скорость велосипедного колеса увеличилась в 2 раза. Как изменилась линейная скорость точек на ободе?
1) увеличился наполовину 2) уменьшился наполовину 3) увеличился наполовину 4) не изменился
6. линейная скорость точек на лопасти винта вертолета уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) остался прежним 2) уменьшился в 16 раз 3) уменьшился 4) уменьшился в 2 раза
7) Радиус движения тела по окружности увеличился в три раза без изменения его линейной скорости. Как изменилось центростремительное ускорение тела?
1) 9 раз увеличился 2) 9 раз уменьшился 3) 3 раза уменьшился 4) 3 раза увеличился
8. сколько времени вращается коленчатый вал двигателя, если он совершает 600 000 оборотов за 3 минуты?
1) 200 000 с 2) 3 300 с 3) 3- 1 0-4 с 4) 5-1 0-6 с
9) Какова частота вращения точки на ободе колеса, если период вращения равен 0,05 с?
1) 0,05 Гц 2) 2 Гц 3) 20 Гц 4) 200 Гц
10) Линейная скорость точки на ободе велосипеда радиусом 35 см равна 5 м/с. Как долго вращается колесо?
1) 14 секунд 2) 7 секунд 3) 0,07 секунды 4) 0,44 секунды
Соотнесите физические величины в левом столбце с соответствующими расчетными формулами в правом столбце. В таблице под номером физической величины в левой колонке напишите соответствующий номер выбранной вами формулы в правой колонке.
ФИЗИЧЕСКИЙ ПЕРЕХОД A) Линейная скорость B) Угловая скорость C) Частота вращения
ОПРЕДЕЛЕНИЕ 1) \( 1/T \) 2) \( v^2/R \) 3) \( v/R \) 4) \( \omega R \) 5) \( 1/n \)
12) Время вращения колеса увеличилось. Как изменились угловая и линейная скорости точки на ободе и ее центростремительное ускорение? Установите соответствие между физическими величинами в левой колонке и характером их изменения в правой колонке. В таблице под номером физической величины в левой колонке напишите соответствующий номер выбранного вами предмета в правой колонке.
ЕСТЕСТВЕННЫЕ ИЗМЕНЕНИЯ A) Угловая скорость B) Линейная скорость C) Центростремительное ускорение








