Это уравнение, которое связывает микроскопические детали или микросостояния системы (через W ) с ее макроскопическим состоянием (через энтропию S ), является центральной идеей статистической механики. Его значение настолько велико, что оно выгравировано на надгробной плите Больцмана.
Физический смысл и формула постоянной Больцмана
Талантливый Людвиг Больцман — один из величайших ученых 19 века. В свое время он внес наибольший вклад в развитие молекулярно-кинетической теории.
- Краткое описание
- Основное соотношение температуры и энергии
- Распределение молекул статистическим образом
- Ключевые нюансы
- Способы нахождения постоянной Больцмана
- Физическая константа
Благодаря своей целеустремленности Больцман стал одним из главных основателей статической механики.
Краткое описание
Людвиг был автором гибкой эргодической гипотезы, статистического метода для детальной интерпретации идеального газа на основе уравнения физической кинетики. Больцман много работал над тем, чтобы ввести термодинамику в общественное сознание.
В результате он смог вывести теорему, подробно описывающую статистический принцип для второго закона термодинамики.

Физики ценят взгляды Больцмана, потому что он смог описать теорию излучения во многих экспериментах. В своих работах он неоднократно ссылался на электродинамику и оптику. Имя этого талантливого ученого было увековечено сразу в двух физических константах.
В свое время Больцман был сильным и последовательным сторонником теории многогранной атомной и молекулярной структуры материи. В течение многих лет ему приходилось сталкиваться с непониманием и негативными комментариями о его работе в научном сообществе того времени. Многие физики считали, что молекулы и атомы — это ненужная абстракция.
Коллеги Больцмана были очень консервативны, что повергло одаренного физика в депрессию, от которой он так и не смог оправиться. Он покончил жизнь самоубийством.
На его могильной плите было выгравировано уравнение S = k * logW в знак признательности за его заслуги. В этом уравнении постоянная k является произведением постоянной Больцмана. При решении задач необходимо учитывать размерность физической величины.
Основное соотношение температуры и энергии
Традиционная модель идеального газа активно используется для правильного расчета состояний реального вещества при давлениях и температурах, близких к нормальным.
В этом случае размер молекулы намного меньше объема, занимаемого данным количеством газа. Но расстояние между частицами гораздо больше, чем радиус, возникающий в результате их тесного взаимодействия. В кинетической теории все необходимые понятия уравнения четко описаны.
Для определения средней энергии этих частиц используется следующая формула. Декодирование выполняется следующим образом:
- Т — температура.
- Е — кинетическая энергия.
- 3,2* k — используемый коэффициент пропорциональности.

В данном случае используется число 3, которое обозначает количество степеней свободы транспортного движения частиц в трех пространственных измерениях.
Но через некоторое время значение k было названо постоянной Больцмана в честь австрийского физика. Этот термин указывает, сколько энергии или джоулей содержит один градус.
Значение константы определяет, насколько именно может статистически увеличиться хаотическая энергия отдельного фрагмента идеального газа при повышении температуры на 1°. Полная энергия теплового излучения определяется законом Стефана-Больцмана.
Связь между этой константой и другими фундаментальными константами можно определить, приравняв значение средней энергии молекул, находящихся в разных модах.
Физический смысл постоянной Больцмана
Исторически температура была впервые введена как термодинамическая величина, и была установлена единица измерения — градус (см. §3.2). После того как была установлена связь между температурой и средней кинетической энергией молекул, стало очевидно, что температура может быть определена как средняя кинетическая энергия молекул и выражена в джоулях или эргах, т.е. вместо T вводится значение T*, так что
Определенная таким образом температура связана с температурой, выраженной в градусах, следующим образом:
Поэтому постоянную Больцмана можно рассматривать как величину, связывающую температуру, выраженную в единицах энергии, с температурой, выраженной в градусах.
Зависимость давления газа от концентрации его молекул и температуры
Выражение E из соотношения (4.5.5) и подстановка его в формулу (4.4.10) дает выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
Из формулы (4.5.6) следует, что при одинаковом давлении и температуре молекулярная концентрация всех газов одинакова.
Из этого следует закон Авогадро: равные объемы газов при одинаковой температуре и давлении содержат одинаковое число молекул.
Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Коэффициент пропорциональности, постоянная Больцмана k = 1 0-23 Дж/К, должен быть выучен наизусть.
§ 4.6. Распределение максвелла
Во многих случаях одного знания средних значений физических величин недостаточно. Например, знание среднего роста людей не позволяет планировать производство одежды разных размеров. Необходимо знать примерное количество людей, чей рост находится в определенном диапазоне. Аналогично, важно знать количество молекул, скорость которых отклоняется от среднего значения. Максвелл был первым, кто понял, как определить эти числа.
В разделе 4.1 мы уже упоминали, что Дж. Максвелл ввел понятие вероятности для описания поведения большой совокупности молекул.
Уже несколько раз отмечалось, что в принципе невозможно определить изменение скорости (или импульса) молекулы за длительный период времени. Даже скорости всех молекул в газе в определенный момент времени не могут быть точно определены. Никаких конкретных значений для скоростей молекул не нужно выводить из макроскопических условий, в которых находится газ (конкретный объем и температура). Скорость молекулы может быть определена случайным образом и может принимать случайные значения в макроскопических условиях, подобно тому, как при броске игральной кости может выпасть любое количество очков от 1 до 6 (число граней игральной кости равно шести). Невозможно предсказать количество очков, которое выпадет на игральной кости. Но вероятность получения, скажем, пяти очков можно определить.
Какова вероятность случайного события? Предположим, что у нас есть очень большое количество N испытаний (N — количество бросков игральной кости). Тогда вероятность этого события равна отношению числа благоприятных случаев к общему числу испытаний, при условии, что это число как можно больше:
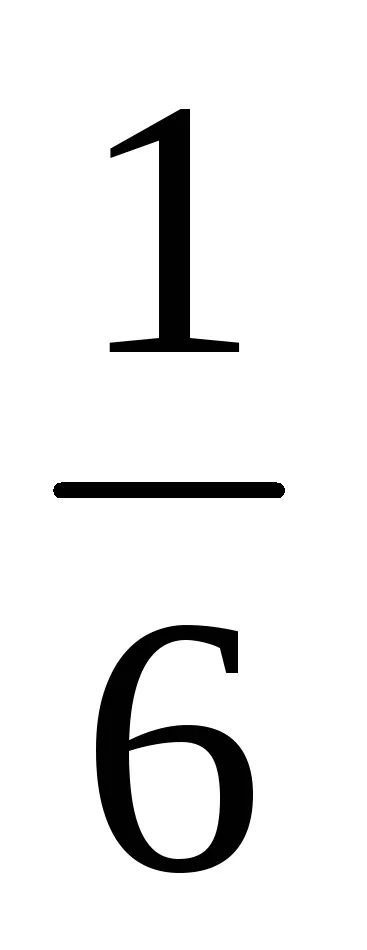
Для симметричного кубика вероятность выпадения любого числа очков от 1 до 6 равна .
Мы видим, что из серии случайных событий вытекает определенная количественная закономерность, появляется число. С помощью этого числа — вероятности — мы можем рассчитать средние значения. Таким образом, если вы бросаете игральную кость 300 раз, среднее количество копеек, как следует из формулы (4.6.1), равно 300 -= 50, и нет никакой разницы, бросаете ли вы одну и ту же кость 300 раз или 300 одинаковых костей одновременно.
Несомненно, поведение молекул газа в контейнере гораздо сложнее, чем движение куба. Но и здесь мы можем надеяться найти некоторые количественные закономерности, которые позволят нам вычислить статистические средние, если только мы ставим проблему как в теории игр, а не как в классической механике. Мы должны отказаться от неразрешимой проблемы определения точного значения скорости молекулы в данный момент и попытаться определить вероятность того, что скорость имеет определенное значение.
Суть проблемы
Представим, что мы находимся в конце XIX века и не знаем, что воздух состоит из молекул. Как мы можем объяснить, что он расширяется при нагревании? А в чем причина потепления в целом? Что такое температура? Какое отношение это имеет к энергии? Атомные формулы статистической механики и термодинамики — вот ответ.
Теперь мы знаем, что температура газа зависит от кинетической энергии его молекул. А давление возникает из-за упругих столкновений атомов со стенками. Но как вычислить порог, который позволит нам перейти от квантовых систем к макрообъектам?
Формула
Такую возможность дает наша константа. Энергия рассчитывается по следующей формуле:
1/2mv²=Tk
Где m — масса молекул газа, v — их скорость, T — результирующая температура и k — постоянная Больцмана. Она равна 1,38 x 1 0-23 Дж/К.
Таким образом, в левой части формулы мы видим характеристики атомного микромира — массу и скорость молекул. С правой стороны находятся характеристики макромира, которые мы можем измерить с помощью доступных инструментов — термометра. Мост готов.
Давайте немного отвлечемся от основной темы. Знаете ли вы, что автор нашей константы известен своей философской концепцией мозга Больцмана? Согласно этому, вероятность возникновения интеллекта в результате флуктуаций (т.е. случайных, мгновенных) выше, чем вероятность его возникновения в результате эволюции. Если предположить, что срок жизни Вселенной не конечен.
Способы вычисления константы
Существует два основных способа определения коэффициента Больцмана:
- Через уравнение идеального газа.
- Через формулу броуновского движения.
Первый способ расчета коэффициента прост. Первый — самый простой способ расчета коэффициента. Изменение температуры мы измеряем термометром, а изменение давления — манометром. Если мы знаем число Авогадро и объем, мы подставляем эти значения в формулу для идеального газа (pV=vRT) и получаем k.
Второй способ более сложный и поэтому описан лишь вкратце для ясности. Думали ли вы когда-нибудь о том, как проще всего перенести броуновское движение молекул в макромир? Вы можете купить зеркало, висящее на веревке в комнате. Молекулы воздуха создают упругое воздействие на зеркало. Если направить на него луч света, то можно зафиксировать даже самые маленькие изгибы.
Рассчитав определенные параметры, такие как модуль кручения, момент инерции зеркала и температура в помещении, мы можем определить k.








