Пример 4: Тело брошено вверх на расстоянии 2 м от земли с начальной скоростью 10 м/с. Найдите высоту тела по отношению к земле, когда оно достигает вершины движения.
9 класс
Гравитация действует на все тела на Земле: неподвижные и движущиеся тела на поверхности Земли и вблизи нее.
Тело, свободно падающее на землю, движется с возрастающим ускорением, поскольку его скорость соосна с силой тяжести и ускорением, обусловленным силой тяжести.
Тело, брошенное вверх без сопротивления воздуха, также движется с постоянным ускорением под действием силы тяжести. Но в этом случае начальная скорость u0на которую было брошено тело, направлена вверх, т.е. против силы тяжести и ускорения, обусловленного гравитацией. Поэтому скорость тела уменьшается (за каждую секунду на величину, численно равную коэффициенту ускорения силы тяжести, т.е. на 9,8 м/с).
Через некоторое время тело достигает наибольшей высоты и в какой-то момент останавливается, т.е. его скорость равна нулю. Понятно, что чем больше начальная скорость тела, тем больше время подъема и тем больше высота, на которую оно поднимается до остановки.
Затем, под действием силы тяжести, тело начинает падать вниз с тем же ускорением.
При решении задач, связанных с движением тела вверх под действием только силы тяжести, используются те же формулы, что и для прямолинейного равномерно ускоренного движения с начальной скоростью axзаменяется на gx:
При этом учитывается, что при движении вверх вектор скорости и вектор гравитационного ускорения направлены в противоположные стороны, поэтому их проекции всегда имеют разные знаки.
Например, если ось x направлена вертикально вверх, т.е. коаксиально вектору скорости, ux>0, тогда ux= u, и gx<0, значит, gx= — g = -9,8 м/с2 (где u — мера мгновенной скорости, а g — мера вектора ускорения).
Если ось x направлена вертикально вниз, то u — этоx<0, т. е. υx= -y, gx>0, т.е. gx= g = 9,8 м/с2 .
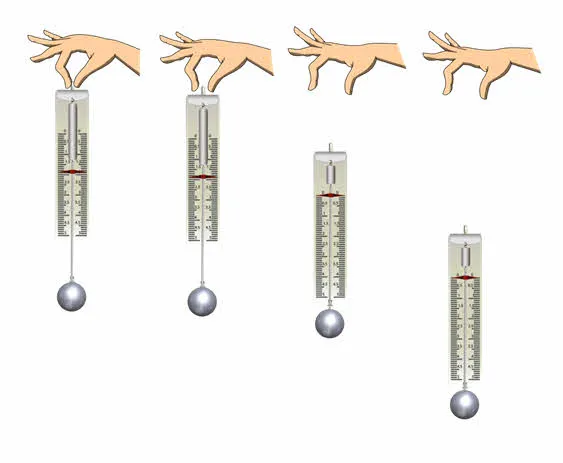
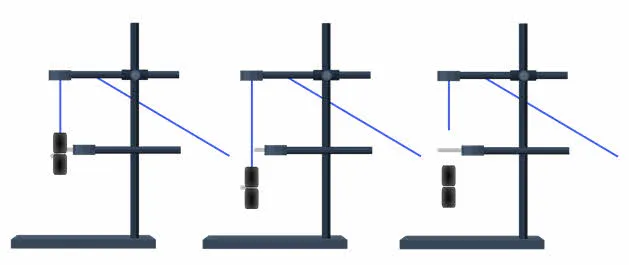
Вес тела, движущегося только под действием силы тяжести, равен нулю. Это видно из экспериментов, показанных на рисунке 31.
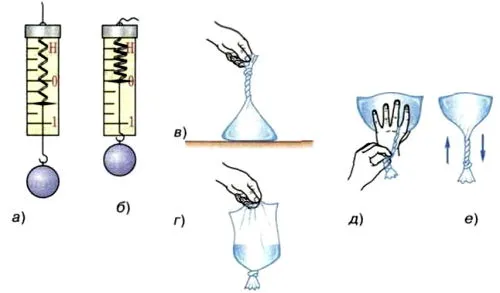
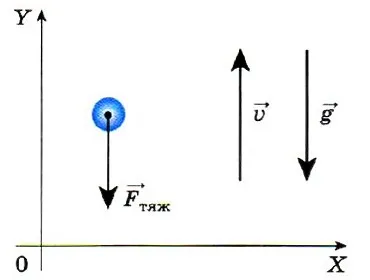
Рисунок 31: Демонстрация невесомости тел в свободном падении.
Металлический шар подвешен к импровизированному динамометру. Масса шарика (рис. 31, a) равна 0,5 Н согласно показаниям динамометра в состоянии покоя. Если нить, на которой закреплен динамометр, перерезана, шарик падает свободно (сопротивлением воздуха в этом случае можно пренебречь). В этом случае указатель перемещается к нулю, указывая на то, что вес шарика равен нулю (рис. 31, б). Вес свободно падающего силоизмерительного прибора также равен нулю. В этом случае и мяч, и динамометр движутся с одинаковым ускорением и не влияют друг на друга. Другими словами, и динамометр, и шар находятся в состоянии невесомости. 1.
Вопросы:
1. действует ли гравитация на тело, брошенное вверх по мере его подъема?
2. с каким ускорением движется поднятое тело без трения? Как изменяется скорость движения?
3 Какова максимальная высота подъема тела, если сопротивлением воздуха можно пренебречь?
4 Что можно сказать о знаках проекций векторов мгновенной скорости тела и ускорения свободного падения в случае свободного движения этого тела вверх?
5. опишите ход экспериментов, показанных на рисунке 31. Какой вывод можно сделать из этого?
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно медленно с начальной скоростью u0 и ускорением a = -g. Перемещение тела за время t — это высота подъема h:
U0 — начальная скорость движения тела U — скорость падения тела в момент времени t g — ускорение свободного падения, 9,81 (м/с;) h — высота, на которую поднимается тело в момент времени t — время.
Скорость тела на данной высоте:
Максимальная высота подъема тела:
Время подъема на максимальную высоту:
Сложение движений, направленных под углом друг к другу.
Тело может одновременно участвовать в нескольких транспортных движениях. Поскольку ускорение, скорость и перемещение являются векторными величинами, их можно складывать по законам векторного (геометрического) сложения. То есть, по правилу параллелограмма.
Величина компонента каждого признака движения может быть рассчитана.
Если: Up — результирующая мгновенная скорость, U1 — мгновенная скорость первого движения, U2 — мгновенная скорость второго движения, ? — угол, образованный векторами скоростей u1 и u2, то по теореме косинусов получаем
Если движения 1 и 2 перпендикулярны друг другу, то формула упрощается, так как
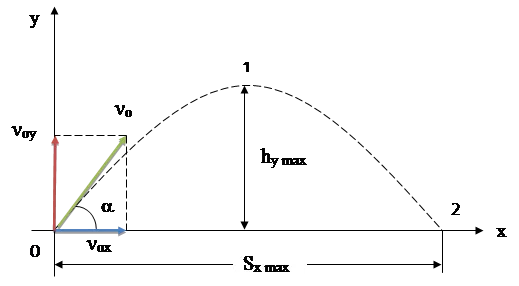
Движение тела, брошенного горизонтально.
Движение горизонтально брошенного тела представляет собой комбинацию двух взаимно перпендикулярных движений: — горизонтального (равномерного) движения, — вертикального (движения свободного падения).
Если построить траекторию движения горизонтально брошенного тела в системе координат xy, приняв точку броска за точку отсчета, а направление оси прямой совпадает с направлением вектора ускорения свободного падения, то координаты каждой точки траектории представляют собой движение тела в горизонтальном направлении (движение с постоянной скоростью U0 ) и в вертикальном направлении (равномерно ускоренное движение с ускорением g).
x, y — координаты тела, u0 — начальная скорость тела (м/с), g — ускорение свободного падения 9,81 (м/с2), t — время движения (c).
Уравнение для траектории горизонтально брошенного тела выглядит следующим образом:
Поскольку ускорение силы тяжести g и начальная скорость u0 постоянны, y пропорционально квадрату x, т.е. траектория представляет собой параболу, вершина которой лежит в начальной точке движения.
УРАВНЕНИЕ ДВИЖЕНИЯ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
Поскольку движение тела, брошенного вертикально вверх, равномерное, то зависимость проекции его движения от времени описывается следующей формулой.
Поскольку ускорение под действием силы тяжести и ось направлены в противоположные стороны, проекция ускорения под действием силы тяжести отрицательна, и мы можем написать
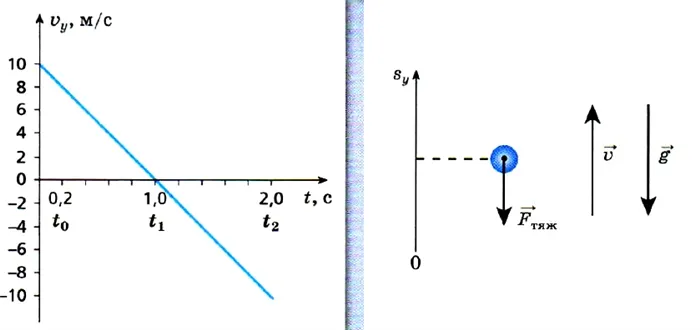
Зависимость координаты тела от времени, т.е. его уравнение движения, в данном случае.
МАКСИМАЛЬНАЯ ВЫСОТА ПОДЪЕМА ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
Жизненный опыт показывает, что чем больше начальная скорость тела, брошенного вертикально вверх, тем выше оно становится. Теперь определим, какова максимальная высота подъема h.
Очевидно, что эта высота соответствует моменту остановки тела, т.е. в момент времени t1. Тогда в соответствии с формулой (2)
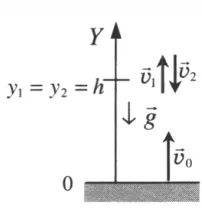
Максимальная высота подъема тела может быть получена из уравнения движения (4) путем подстановки значения t1. Поскольку нас интересует, насколько высоко поднялось тело по отношению к своему начальному положению, значение y0можно считать равным нулю:
Таким образом, максимальная высота подъема тела, брошенного вертикально вверх, пропорциональна квадрату его начальной скорости.
Согласно уравнению (5), максимальная высота подъема тела, брошенного вертикально вверх, зависит только от его начальной скорости, но не от его массы и формы. Важно понимать, что это верно только в том случае, если не учитывать сопротивление воздуха. В реальных условиях максимальная высота, на которую может подняться тело, меньше значения, полученного из формулы (5), из-за сопротивления воздуха.
Вы просмотрели урок физики 9 «Движение тела, брошенного вертикально вверх».
Движения тела, брошенного вертикально вверх. Невесомость
В этом уроке мы выясним, с каким ускорением движется тело, брошенное вертикально вверх. Мы выясним, как меняется скорость тела во время этого движения. Мы научимся рассчитывать максимальную высоту тела и время движения. Мы также узнаем, что такое состояние тела называется гравитационной инерцией.
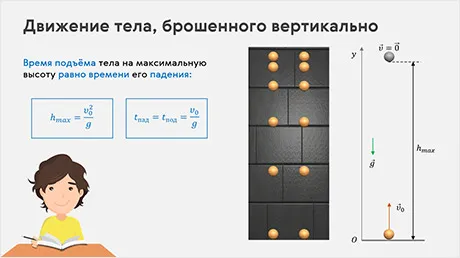
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим учебным видео в этом наборе, вам нужно добавить его в свой личный шкафчик.

2. Распространите видеоуроки среди своих учеников в личных кабинетах.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Движения тела, брошенного вертикально вверх. Невесомость»
Движение тела, движущегося вертикально вверх без сил сопротивления, также является изоускоренным и происходит в ускоренном свободном падении. Дело в том, что толчок тела вверх не может изменить силу тяжести, действующую на тело. Поэтому ни направление, ни численное значение ускорения тела не меняется.
Вы смотрите на стробоскопическое изображение движения тела, выстреливаемого вертикально вверх с определенной начальной скоростью.

Это показывает, что тело постепенно уменьшает свою скорость по мере движения вверх. Каждую секунду она уменьшается на величину, численно равную величине ускорения под действием силы тяжести. Через некоторое время тело достигает высшей точки подъема и останавливается на некоторое время, что означает, что его скорость становится нулевой. Когда достигнута высшая точка подъема, тело начинает свободно падать под действием силы тяжести, проходя через те же позиции, что и во время подъема.
В прошлом уроке мы показали, что в свободном падении тело движется с равновесной скоростью. Поэтому для описания движения тела вверх и вниз можно использовать кинематическое уравнение равноускоренного движения и уравнение скорости в проекциях на оси координат.
Давайте подробно рассмотрим движение тела вверх.

Мы хотели бы обратить ваше внимание на то, что силу тяжести, действующую на свободно падающее тело, не следует путать с весом тела. Вес тела фактически определяется как сила, с которой тело действует на опору или подвес. Это означает, что сила тяжести действует на тело, а вес переносится на опору или подвеску. Природа гравитации и веса также различна. Гравитация имеет гравитационное происхождение, в то время как вес является частным случаем упругой силы, то есть электромагнитной силы.
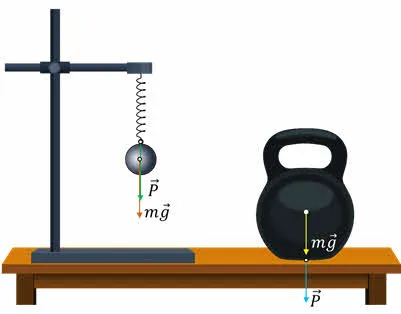
Чтобы проиллюстрировать это различие, рассмотрим тело в подъемной камере, движущееся вниз с некоторым ускорением. Со стороны земли на тело действует сила тяжести, со стороны опоры на тело действует сила реакции опоры, а со стороны опоры на тело действует вес опоры. Согласно третьему закону Ньютона, вес тела равен и противоположен силе нормальной реакции опоры.

Формула также показывает, что в случае свободного падения тела его вес равен нулю. Такое состояние тела называется невесомостью.
Тот факт, что вес тела на самом деле равен нулю, также можно проверить экспериментально.
Возьмем динамометр и подвешенный к нему груз. Когда динамометр находится в состоянии покоя по отношению к Земле, он показывает, что вес тела равен силе тяжести. Теперь отпустите динамометр. Легко заметить, что игла динамометра находится на нуле, что означает, что вес тела равен нулю.