Неотъемлемой частью нашей жизни является движение. Люди, автомобили, самолеты, космические корабли и планеты движутся. Молекулы, атомы, ионы и электроны движутся. В окружающем нас мире все находится в постоянном движении. Как сказал древнегреческий философ Гераклит: «Все течет, все изменяется. И невозможно дважды войти в одну и ту же реку».
Понятие «материальная точка»
Понятие «материальная точка» — это абстракция. Материальные точки не существуют в природе. Однако постановка некоторых задач в механике дает возможность использовать эту абстракцию.
Когда мы говорим о точке в кинематике, ее можно рассматривать как математическую точку. В кинематике под точкой понимается небольшой след на теле или само тело, если его размеры малы по сравнению с расстояниями, которые проходит тело.
В такой части механики, как динамика, мы уже должны говорить о материальной точке как о точке, обладающей массой. Основные законы классической механики относятся к материальной точке, телу, которое не имеет геометрических размеров, но обладает массой.
В динамике во многих случаях размер и форма тела не влияют на характер движения, поэтому тело можно считать материальной точкой. В других случаях, однако, само тело нельзя считать точкой, поскольку его форма и размер имеют решающее значение для описания движения тела.
Поэтому если вас интересует, сколько времени занимает путь автомобиля от Москвы до Тюмени, вам не нужно знать, как движутся отдельные колеса автомобиля. Но если водитель пытается втиснуть свой автомобиль в тесное парковочное пространство, неправильно думать об автомобиле как о физической точке, потому что размеры автомобиля имеют значение. Вы можете рассматривать Землю как физическую точку, когда смотрите на движение нашей планеты вокруг солнца, но вы не можете сделать то же самое при изучении ее движения вокруг своей оси, когда пытаетесь определить причины чередования дня и ночи. Таким образом, одно и то же тело может считаться материальной точкой при одних обстоятельствах, но не при других.
Существуют определенные виды движения, в которых тело можно свободно рассматривать как материальную точку. Например, при поступательном движении твердого тела все его части движутся равномерно, поэтому при таком движении тело обычно рассматривается как точка с массой, равной массе тела. Однако когда то же самое тело вращается вокруг своей оси, его нельзя считать материальной точкой.
Поэтому материальная точка является простейшей моделью тела. Если тело можно сравнить с материальной точкой, это значительно упрощает изучение его движения.
Различные типы движения точки сначала различают по типу траектории. Если траектория движения точки представляет собой прямую линию, то движение называется прямолинейным. При движении макроскопического тела говорить о прямолинейном или криволинейном движении тела имеет смысл только в том случае, если можно описать движение точки тела. В теле различные точки могут выполнять различные типы движений.
Система материальных точек
Если тело нельзя рассматривать как материальную точку, его можно представить как систему материальных точек. В этом случае тело мысленно делится на бесконечно малые элементы, каждый из которых можно рассматривать как материальную точку.
В механике любое тело можно представить как систему материальных точек. Поскольку мы знаем законы движения точки, мы можем предположить, что у нас есть метод описания любого тела.
В механике существенную роль играет понятие абсолютно твердого тела, определяемого как система материальных точек, расстояния между которыми постоянны при всех взаимодействиях этого тела.
Примеры задач с решением
Задача. В этом случае тело можно рассматривать как материальную точку:
Спортсмен бросает ядро во время забега. Можно ли считать ядро существенной точкой?
Шар вращается вокруг своей оси. Является ли мяч материальной точкой?
Гимнастка выполняет упражнение на брусьях.
Бегун проходит дистанцию.
Ответ. 1) Шар можно рассматривать как материальную точку.
2) Вращающийся шар нельзя рассматривать как материальную точку, так как при описании его вращения необходимо учитывать, что различные точки шара во время этого движения движутся по-разному.
3) Гимнастка не может считаться материальной точкой.
4) Бегуна можно считать материальной точкой, если нет необходимости детально исследовать его бег, особенно на финише, например, с помощью фотографической мишени.
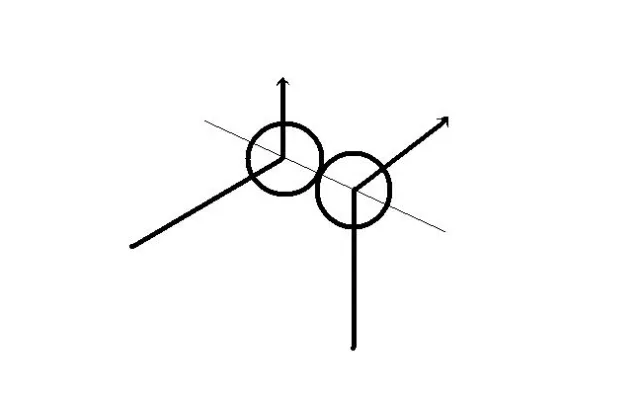
Задача. При каких обстоятельствах камень, движущийся вверх, может считаться материальной точкой? См. рис. 1 и рис. 2.

Решение: На рис.1 размер камня нельзя считать маленьким по отношению к расстоянию до него. В этом случае камень не может считаться материальной точкой.
На рис. 2 камень вращается, поэтому его нельзя считать материальной точкой.
Реакция. Камень, брошенный вверх, можно считать материальной точкой, если его размеры малы по отношению к расстоянию и он движется поступательно (не вращается).

Проверенные писатели готовы помочь вам написать документ любой сложности
Мы уже помогли 4 396 студентам сдать работы от решения задач до получения диплома с отличием! Определите стоимость вашей работы за 15 минут!
Важные характеристики объектов
Все законы физики предназначены для описания явлений в нашем обычном мире в трехмерном пространстве. И все законы относятся к физическим объектам, которые имеют определенный размер, форму, массу и ряд других свойств.

Но каждый закон описывает только один аспект явления. И для его описания большинство свойств объекта излишни. Независимо от этого, явление будет происходить точно так же. Например, для описания работы весов не имеет значения, какую форму имеют взвешиваемые предметы. Форма объектов также не имеет значения для описания равномерного линейного движения.
Так, в физике часто возникает ситуация, когда законы и описания относятся только к важным характеристикам описываемых объектов и явлений, а все остальные характеристики не влияют на поведение объектов и просто игнорируются.
Понятие материальной точки
При описании движения объектов необходимо определить их положение в пространстве. В этом случае часто (но не всегда) оказывается, что информация о форме объекта не нужна. Достаточно описать движение только одной точки объекта, остальные точки движутся точно так же. Поэтому большинство законов движения тел описывают движение одной точки объекта.
Эта точка называется «материальной точкой».
Примерами материальных точек в природе являются планеты при описании их движения вокруг солнца, отдельные пешеходы или автомобили в движении, отдельные молекулы газа и многие другие.

Один и тот же объект может быть или не быть материальной точкой, в зависимости от обстоятельств описываемого явления. Если два шара сталкиваются лоб в лоб вдоль прямой линии, а затем оба отскакивают вдоль той же прямой линии, то шары можно считать материальными точками. Если одинаковые шарики с одинаковыми скоростями сталкиваются не «лоб в лоб», а «по касательной» и отскакивают по разным прямым — тогда шарики нельзя считать материальными точками, а нужно учитывать их размеры.
Характеристики материальной точки
Материальная точка, как и геометрическая точка, — это наименьшая часть объекта в пространстве, для которой можно определить положение относительно принципа координат.
Материальной точкой может быть любой объект, размерами и формой которого можно пренебречь в условиях задачи. Например, если путь объекта намного больше его размера. Путь объекта также может быть коротким, но если объект не меняет своей формы и ориентации в пространстве, а все его точки движутся равномерно, то его также можно считать материальной точкой.
Фактически, материальная точка — это модель объекта, аналогичная геометрической точке, с одной важной поправкой: материальная точка имеет массу. Если описывается только движение объектов — то масса в этом случае также не нужна. Но если взаимодействие описано, то массой уже нельзя пренебречь.
Таким образом, материальная точка — это объект, размер и форма которого не важны для условий задачи. Характеристики материальной точки включают координаты в пространстве и постоянную массу.
Материальная точка
Материальная точка — это идеализированная концепция. Введение этого понятия абстрагирует от всех свойств тела, которые не имеют отношения к конкретному движению, например, его размер, форма, структура и т.д.
Каждая материальная точка, движущаяся в пространстве, описывается воображаемой линией, так называемой траекторией, которая может иметь множество форм.
Если траектория точки — прямая линия, то движение называется прямолинейным; если кривая линия, то движение называется криволинейным.
Как определить материальную току
Положение тела или материальной точки определяется только по отношению к другому материальному телу, которое обычно считается неподвижным и называется телом отсчета.
Произвольная система координат, связанная с этой системой отсчета, называется системой отсчета для положения материальной точки. Без выбора системы отсчета невозможно описать движение.
В случае прямолинейных движений, например, можно использовать систему координат, состоящую из прямой линии OS, вдоль которой происходит движение и которая начинается в точке O.
Кинетика Декарта
В более сложных случаях используется декартова прямоугольная система координат, в которой оси O и O перпендикулярны друг другу и пересекаются в точке O, которая является началом координат.
Длина части траектории, которую точка проходит от временного начала, называется длиной пути. Путь — это скалярная величина, характеризуемая только числовым значением s.
Если соединить начальное положение точки с ее конечным положением, то получится перемещение ∆ r точки за определенное время t .
Смещение точки является вектором, т.е. величиной, характеризующейся числовым значением и направлением. При линейном движении абсолютная величина вектора перемещения |∆ r | равна пути s.
Различают два основных и более простых вида движения твердого тела: поступательное и вращательное.
Движение тела, при котором линия, соединяющая две точки тела, перемещается параллельно самой себе по мере движения тела, называется поступательным движением.
Вращательное движение
Вращательное движение — это движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой (оси вращения).
В зависимости от характера связи пути со временем движение делится на равномерное и неравномерное.
Что мы узнали о материальной точке?
Что из нижеперечисленного является примером материальной точки?
Материальная точка, движение которой в пространстве не ограничено механическими ограничениями, называется свободной точкой.
Примерами свободных материальных точек являются искусственный спутник Земли, вращающийся вокруг Земли, и летящий аэроплан (если пренебречь их вращением).
Что такое материальная точка Малое тело?
Материальная точка — это стандартное понятие (абстракция) в классической механике, обозначающее тело с минимальными размерами, но с некоторой массой.
С одной стороны, материальная точка является самым простым объектом в механике, поскольку ее положение в пространстве определяется всего тремя числами.
Равномерное прямолинейное движение
Равномерное прямолинейное движение — это движение, при котором материальная точка, движущаяся по прямой, проходит пути одинаковой длины за любые равные промежутки времени.
Примером равномерного линейного движения является движение сборочной линии на заводе, поезда по прямому пути с постоянной тягой и т.д.
Однако следует помнить, что в природе не существует идеально равномерного движения, но если отклонения от равномерности незначительны, ими можно пренебречь.
Физическая величина
Физическая величина, численно соответствующая расстоянию, пройденному телом за единицу времени, называется скоростью u.
Для описания движения тела вводится векторная физическая величина — скорость. Положение тела, движущегося по прямой линии в данный момент времени t0определяется s0и в момент времени t — s. Тогда в момент времени t — t0тело движется вдоль линии s — s0.
Мы можем записать математическое выражение для скорости u следующим образом
u = ( s — s0):( t — t0)
В особом случае, когда t0= 0 и s0= О,
u = s : t
Где s означает расстояние, пройденное телом за время t.
Скорость равномерного движения является константой. При прямолинейном движении вектор скорости направлен вдоль траектории.
Единицы измерения
В СИ единицей скорости является скорость равномерно движущегося тела, проходящего расстояние в один метр за одну секунду,
В СГС единицей измерения скорости является 1(см:с) Из формулы (1) получаем
s = s0+ u ( t — t0)
Если t0= 0 и s0= 0, тогда формула (3) дает
s = u t,
где s — расстояние, пройденное телом за время t.
Формула (4) показывает, что путь тела при его прямолинейном движении является линейной функцией времени, так как u — постоянная величина.
Что мы узнали о равномерное прямолинейное движение?
Как найти линейное перемещение?
Линейное движение аналитически описывается функцией: s = vt, где v = const.
Чем больше мера скорости, тем больший угол s(t) она образует с осью времени.
Какие параметры не изменяются при линейном равномерном движении?
Линейное равномерное движение — это движение по прямой линии, при котором тело совершает равные перемещения через равные промежутки времени.
В этом движении скорость тела не меняется.
Графики скорости пути равномерного движения
Формула s = u t дает полное описание равномерного движения. Связь между s и t для отдельных моментов времени может быть представлена в виде таблицы, содержащей соответствующие значения для интервала времени и пройденного расстояния.
Например, скорость равномерного движения составляет 0,5 -. Формула (4) в этом случае имеет вид s = 0,5 — t. Таблица расстояния и времени этого движения выглядит следующим образом:
| т, с | 0 | 1 | 2 | 3 | 4 |
| s, М | 0 | 0,5 | 1 | 1,5 | 2 |
Зависимость от времени в пути удобнее показать на диаграмме. Они более наглядно показывают, как изменяется перемещение в зависимости от времени.
Пример расчета по графику движения
Отложим на оси вершин значение времени t (рис. 1), а на оси ординат — значение пути s. Тогда перемещение s как функция времени t выражается линией OA.
Если тело движется с большей скоростью (u = 1,25(м:с), то эта зависимость выражается линией OB. Линии OA и OB называются графами путей.

По графику пути равномерного движения можно определить скорость, с которой совершалось движение.
Тангенс угла a наклона графика пути к оси времени численно равен отношению ординаты любой точки графика к его абсциссе, т.е. равен отношению s : t, что является скоростью равномерного движения.
Поэтому u равно tg a. Чем больше скорость, тем больше угол между кривой и осью времени.
Рис. 1-2 Диаграммы пути-скорости для равномерного движения
На рисунке 2 показан график равномерной скорости, полученный следующим образом: На оси абсцисс представлено значение времени, а на оси ординат — значение скорости, которая не меняется со временем (u = 3 (м:с) = постоянная).
Здесь график скорости равномерного движения представляет собой прямую AB, параллельную оси времени. Используя график скорости, мы можем определить расстояние, которое проходит тело за данный промежуток времени.
Для равномерного прямолинейного движения расстояние s, пройденное телом, численно равно площади прямоугольника, ограниченного осью времени, графиком скорости и двумя вертикальными отрезками, исходящими из точек, соответствующих началу и концу рассматриваемого интервала времени.
Характеристики материальной точки
Материальная точка, как и геометрическая точка, — это наименьшая часть объекта в пространстве, для которой можно определить положение относительно принципа координат.
Материальной точкой может быть любой объект, размерами и формой которого можно пренебречь в условиях задачи. Например, если путь объекта намного больше его размера. Путь объекта также может быть коротким, но если объект не меняет своей формы и ориентации в пространстве, а все его точки движутся равномерно, то его также можно считать материальной точкой.
Фактически, материальная точка — это модель объекта, аналогичная геометрической точке, с одной важной поправкой: материальная точка имеет массу. Если описывается только движение объектов — то масса в этом случае также не нужна. Но если взаимодействие описано, то массой уже нельзя пренебречь.
Таким образом, материальная точка — это объект, размер и форма которого не важны для условий задачи. Характеристики материальной точки включают координаты в пространстве и постоянную массу.
Актуальные вопросы теории и практики современного образования
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курс «Инфоурок»).
В настоящее время накопительная скидка (от 2% до 25%) доступна для 54 337 учреждений. Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет InforoLesson.


«Инновация. Инновационные технологии»


2 слайд Что такое инженерия движения? Что такое траектория? Что такое равномерное движение? Что такое поступательное движение? Что такое скорость тела? Как можно определить скорость тела, если известны расстояние и время? Отзыв.

3 слайд Механическое движение Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

4 Слайд Траектория Траектория — это линия, описываемая движущимся телом.
5 Слайд Равномерное движение Движение с постоянной скоростью.

6 Слайд Поступательное движение Тело движется равномерно, если все его точки движутся равномерно.

7 слайд Скорость тела Скорость — это физическая величина, которая описывает, как быстро изменяется скорость тела.

8 Слайд Что такое материальная точка? Всегда ли можно применять термин «материальная точка»? Что такое система отсчета? Из чего состоит система отсчета?
Материальная точка Система отсчета

Слайд 9 При решении различных научных и практических задач, связанных с механическим движением тел, необходимо уметь описывать движение

10 Слайд 10 Опишите движение тела Определите путь движения Определите скорость движения Определите расстояние, пройденное телом Определите положение тела в пространстве и т.д.








