Магнитная цепь — Magnetic circuit. Что называют магнитной цепью.

В дополнение к закону Ома, правила Кирхгофа также применимы к магнитным цепям. Первое правило Кирхгофа для магнитных цепей выглядит следующим образом: Алгебраическая сумма магнитных потоков ∑Φ в узле магнитной цепи равна нулю. Чтобы объяснить это правило, представим себе разветвленную магнитную цепь

Магнитные цепи. Законы и параметры магнитных цепей Понятие магнитной цепи

Доброе утро всем. В прошлой статье я рассказал о магнитном поле в веществе, упомянув напряженность магнитного поля, магнитную проницаемость и восприимчивость, а также намагниченность и гистерезис в ферромагнетиках. Однако магнитное поле зависит не только от свойств материи, но и от ее формы. Именно об этом я и хотел бы поговорить в этой статье.

Чтобы собрать радиоэлектронное устройство, вы можете купить набор «Сделай сам» по ссылке.

Что такое магнитная цепь?

Магнитная цепь — это соединение магнитных элементов, к которым приложен магнитный поток. То есть, сердечник, вокруг которого намотана любая катушка, трансформатор, индуктор и т.д., представляет собой магнитную цепь. Если веществом такого сердечника является воздух (т.е. для индукторов без рамки), то это тоже магнитная цепь. Очень часто магнитную цепь называют магнитным кругом, что по сути является тем, чем она является: сердечником, излучающим магнитное поле, подобно тому, как проводник излучает электрический ток. Кроме того, магнитные цепи подчиняются законам электричества: закону Ома, правилам Кирхгофа и т.д., но об этом подробнее ниже.

Магнитные цепи могут быть как однородными, так и неоднородными. Однородные цепи — это магнитные цепи, которые изготовлены из одного и того же материала (т.е. имеют одинаковую магнитную проницаемость) и имеют одинаковое поперечное сечение по всей длине. Если хотя бы одно из этих условий не выполняется, то такая магнитная цепь называется неоднородной.

Различают также разветвленные и неразветвленные магнитные цепи. Разветвленные контуры состоят из одного контура, а разветвленные контуры состоят из нескольких контуров, в которых магнитный поток направляется по контуру. Разветвленные цепи могут быть симметричными или асимметричными. В симметричных контурах магнитный поток одинаков в каждом контуре.

Читайте также: Устройство и принцип работы путевого дроссель-трансформатора, методика расчета

Закон Ома для электрической или магнитной цепи — в чём сходство и различие

Как вы знаете, в законе Ома для электрических цепей упоминаются такие термины, как электродвижущая сила, сопротивление и ток. С другой стороны, известно, что движущиеся электроны генерируют магнитное поле, которое может быть описано векторными величинами, определяемыми по относительно сложным и неочевидным правилам. В качестве примера последнего можно вспомнить правило Буравника, которое определяет направление вектора напряженности магнитного поля как функцию тока, протекающего через проводник.

Несмотря на различия, в некоторых случаях магнитное поле описывается формулой, которая почти точно соответствует закону Ома для электрического тока. Только в этом случае вместо тока используется магнитный поток, вместо электрического тока — магнитное сопротивление, а в качестве электродвижущей силы — электродвижущая сила. Эти два закона имеют сходную форму, но должно быть ясно, что они являются сходной формой выражения двух различных физических явлений.

Подобно тому, как электродвижущая сила (ЭДС) управляет током электрического заряда в электрических цепях, магнитодвижущая сила (ММП) «управляет» магнитным потоком в магнитных цепях. Однако термин «магнитодвижущая сила» является ошибочным, поскольку это не сила и не то, что движется. Возможно, лучше просто назвать это MMF. По аналогии с определением ЭДС, магнитодвижущая сила F>вокруг замкнутого контура определяется как:

F = ∮ CHAS ⋅ d l .= oint mathbf cdot mathrm mathbf .>

ММФ представляет собой потенциал, который гипотетический магнитный заряд получит, совершив цикл. Управляемый магнитный поток — это не то же самое, что ток магнитного заряда; он просто имеет такое же отношение к ММП, как электрический ток к ЭДС (см. ниже подробное описание микроскопических источников сопротивления).

Единицей магнитомеханической силы является ампер-катушка (At), представленная постоянным постоянным электрическим током в один ампер, протекающим в одной петле из электропроводящего материала в вакууме. Гилберта (Gb), введенный МЭК в 1930 году. 1 — это единица магнитодвижущей силы, принятая в ПГС и являющаяся несколько меньшей единицей, чем ампер катушки. Аппарат назван в честь английского врача и натурфилософа Уильяма Гилберта (1544-1603).

Магнитную силу часто можно быстро рассчитать, используя закон Ампера. Например, магнитодвижущая сила F>большой катушки составляет

Где N — число витков, а I — ток в катушке. На практике это уравнение используется для реальных катушек ММФ, где N — число витков индукционной катушки.

Магнитный поток

Используется магнитный поток «диска» ММФ через магнитные элементы системы. Магнитный поток через магнитный элемент пропорционален количеству линий магнитного поля, проходящих через площадь поперечного сечения этого элемента. Это чистое число, т.е. число, идущее в одном направлении, минус число, идущее в другом направлении. По определению, направление вектора магнитного поля B — от южного к северному полюсу магнита внутри магнита; вне магнита линии поля движутся с севера на юг.

Поток через элементарную область, перпендикулярную направлению магнитного поля, определяется произведением магнитного поля и элементарной области. В более общем смысле магнитный поток Ф определяется как скалярное произведение магнитного поля и вектора площади элемента. Количественно, магнитный поток на поверхности S определяется как интеграл магнитного поля по поверхности

Φ m = ∬ S B ⋅ d S .

Для магнитного элемента площадь S, используемая для расчета магнитного потока Φ, обычно выбирается равной площади поперечного сечения элемента.

В СИ единицей магнитного потока является Вебер (в производных единицах: вольт-секунда), а единицей плотности магнитного потока (или «магнитной индукции», B ) является Вебер на квадратный метр или Тесла.

Схемотехнические модели

Наиболее распространенным способом представления магнитной цепи является модель сопротивления, которая проводит аналогию между электрическими и магнитными цепями. Эта модель хороша для систем, содержащих только магнитные компоненты, но для моделирования системы, содержащей как электрические, так и магнитные части, она имеет серьезные недостатки. Он неадекватно моделирует поток тока и энергии между электрической и магнитной областями. Это происходит потому, что электрический резистор высвобождает энергию, а магнитный резистор накапливает ее и высвобождает позже. Альтернативной моделью, которая правильно представляет поток энергии, является модель гироконденсатора.

Модель «сопротивление-сопротивление» для магнитных цепей представляет собой кластерную элементную модель, которая сравнивает электрическое сопротивление с магнитным сопротивлением.

Закон Ома для магнитных цепей

В электронных цепях закон Ома — это эмпирическая зависимость между E>приложенный к элементу, и ток, протекающий через этот элемент. Оно написано следующим образом:

где p — электрическое сопротивление рассматриваемого материала. Существует аналог закона Ома, используемый в магнитных цепях. Этот закон часто называют законом Хопкинсона, в честь Джона Хопкинсона, но на самом деле он был сформулирован ранее Генри Огастусом Роуландом в 1873 году. 3 В нем говорится, что 4 5

где F>магнитодвижущая сила (ММ) в магнитном элементе, Fмагнитный поток через магнитный элемент, а p>магнитное сопротивление этого элемента. (Позже будет показано, что эта связь обусловлена эмпирической зависимостью между полем CHAS и магнитным полем B, B = μ CHAS, где μ — проницаемость материала). Как и закон Ома, закон Хопкинсона можно интерпретировать либо как эмпирическое уравнение, применимое к определенным материалам, либо как определение сопротивления.

Закон Хопкинсона не является корректной аналогией закона Ома с точки зрения моделирования потока мощности и энергии. В частности, нет потерь мощности, связанных с магнитным сопротивлением, так же как нет потерь мощности, связанных с электрическим сопротивлением. Магнитное сопротивление, которое в этом отношении является настоящим аналогом электрического сопротивления, определяется как отношение между магнитодвижущей силой и скоростью изменения магнитного потока. Здесь скорость изменения магнитного потока заменяет электрический ток, и аналогия закона Ома становится следующей:

Где p m>- магнитное сопротивление. Эта зависимость является частью электромагнитной аналогии, называемой моделью конденсаторной петли, и предназначена для преодоления недостатков модели сопротивления. Модель конденсаторного контура, в свою очередь, является частью большей группы совместимых аналогий, используемых для моделирования систем в различных энергетических диапазонах.

Нежелание

Магнитное сопротивление, также называемое магнитосопротивлением, аналогично сопротивлению в электрических цепях (хотя при этом не выделяется магнитная энергия). Подобно тому, как электрическое поле заставляет электрический ток идти по пути наименьшего сопротивления, магнитное поле заставляет магнитный поток идти по пути наименьшего магнитного сопротивления. Это скалярная, большая величина, подобная электрическому сопротивлению.

Параметры магнитных цепей

Как я уже говорил ранее, многие законы для электрических цепей применимы и к магнитным цепям. Чтобы обобщить эти законы, необходимо ввести некоторые параметры, характеризующие магнитные цепи. Представим себе неоднородный и неразветвленный магнитный контур

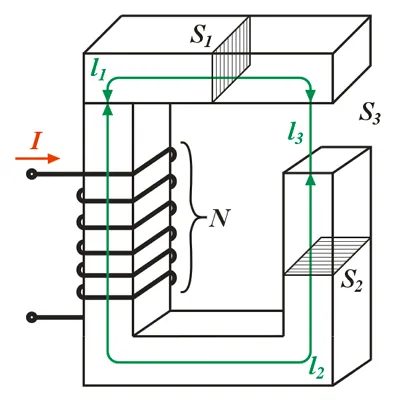
Неоднородный магнитный контур без вентилятора.

Эта цепь состоит из трех сегментов длиной l₁, l₂, l₃с площадью поперечного сечения S_1,S_2,S₃а магнитное поле создается током I, протекающим через электромагнит с N катушками. Поскольку линии магнитного поля в магнитной цепи по существу замкнуты, магнитный поток Φ можно считать одинаковым во всей магнитной цепи, и он определяется следующим выражением.

где B — магнитная индукция,

S — площадь поперечного сечения, через которое проходит магнитный поток.

Таким образом, магнитный поток пропорционален току в электрических цепях.

Согласно закону полного тока и циркуляции вектора магнитной индукции, можно рассчитать следующее уравнение

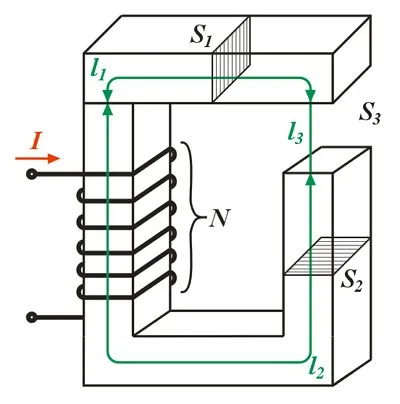
где B₁, В₂, В₃— магнитная индукция в точке l₁, l₂, l₃магнитной цепи,

μ₀— магнитная постоянная, м₀= 4π*1 0-7 Гн/м

μ₁, μ₂, μ₃— или относительная магнитная проницаемость l₁, l₂, l₃ядро

N — количество витков провода,

I — ток, протекающий через провод.

В ферромагнетике определение относительной магнитной проницаемости вызывает некоторые трудности, поэтому в этом законе вместо магнитной индукции мы используем напряженность магнитного поля. Поэтому для данной магнитной цепи закон полного тока можно представить следующим образом.

Если выразить магнитную индукцию через магнитный поток, то получится следующее выражение

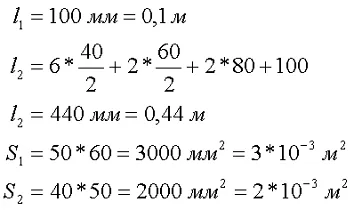
где S_1,S_2,S₃— в каждом случае является площадью поперечного сечения l₁, l₂, l₃магнитной цепи.

По аналогии с электрической цепью, для магнитной цепи получаются следующие параметры

где E_m— магнитодвижущая сила,

R_m— магнитное сопротивление цепи.

Следовательно, вышеприведенное выражение можно выразить следующим образом

где R_m1, R_m1, R_m1— соответственно магнитные сопротивления l₁, l₂, l₃магнитной цепи.

Законы магнитной цепи

Как я уже писал выше, многие законы для электрических цепей применимы и к магнитным цепям. Например, закон Ома для магнитной цепи звучит так: магнитный поток Φ прямо пропорционален магнитной движущей силе E_mи обратно пропорционально полному сопротивлению магнитной цепи R_m. Она выражается следующей формулой, также называемой формулой Хопкинсона.

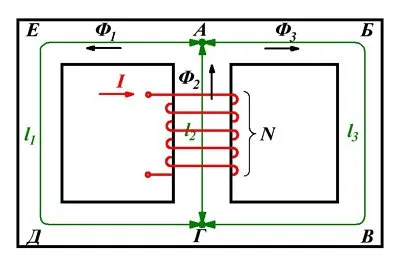
В дополнение к закону Ома, правила Кирхгофа также применимы к магнитным цепям. Таким образом, первый закон Кирхгофа для магнитных цепей гласит, что алгебраическая сумма магнитных потоков ∑Φ в узле магнитной цепи равна нулю. Для иллюстрации этого правила необходимо описать разветвленную магнитную цепь

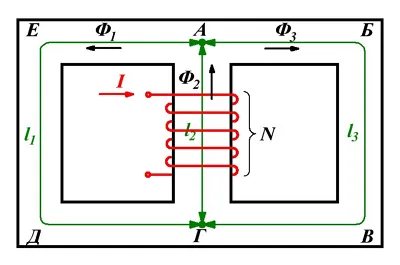
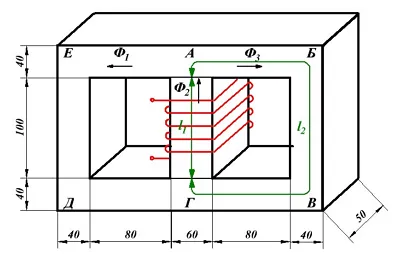
Разветвленная магнитная цепь.

Этот магнитный контур состоит из двух контуров ABVG и AGDE. Ветвь AG генерирует магнитный поток Φ₂который распадается в точке A на два тока Φ₁и Φ₃. Таким образом, в точке A алгебраическая сумма магнитных потоков равна нулю.

Аналогично, второй закон Кирхгофа для магнитной цепи выглядит следующим образом: В магнитной цепи алгебраическая сумма магнитодвижущих сил ∑E_mравна алгебраической сумме магнитных напряжений в отдельных положениях.

Магнитное напряжение в сегменте цепи определяется произведением магнитного потока Φ на магнитное сопротивление сегмента R._mПоэтому второй закон Кирхгофа имеет вид

тогда второй закон Кирхгофа для магнитной цепи, показанной выше, имеет вид

Используя эти соотношения, довольно легко рассчитать необходимые геометрические размеры магнитных контуров для различных магнитных систем, таких как трансформаторы, индукторы, индуктивности и т.д., что мы и сделаем ниже.

Расчёт магнитных цепей

Теория без практического применения не представляет интереса для радиолюбителей. Итак, давайте перейдем к практическому применению теории магнитных цепей. Практический расчет магнитных цепей приводит к определению магнитодвижущей силы E_m(или, иначе, число витков провода N при определенном токе I), который создает определенную магнитную индукцию B (или определенный магнитный поток F). Для этих расчетов необходимо знать геометрические размеры магнитной цепи и магнитную проницаемость материала.

Сначала рассчитаем неразветвленную магнитную цепь, пример которой показан на следующем рисунке.

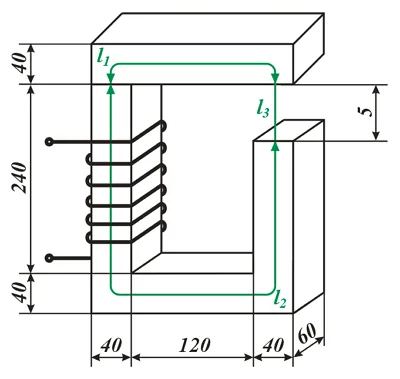
Расчет неразветвленной магнитной цепи (магнитопровода).

Эта магнитная цепь состоит из трех L₁, l₂, l₃из различных материалов. Где l₁— литая сталь, л₂— электросталь, л₃— воздушный вакуум.

Нужно рассчитать число витков N обмотки для создания магнитного потока Φ = 3,6 * 1 0-3 Вб, когда ток, протекающий через обмотку, равен I = 2 А.

Поскольку наша магнитная цепь неоднородна, сначала вычислим среднюю длину магнитных силовых линий l₁, l₂, l₃которая проходит через центр магнитной цепи, и поперечное сечение магнитной цепи S.

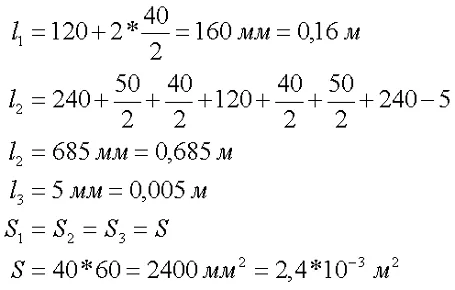
Затем вычисляем магнитную индукцию отдельных секций l₁, l₂, l₃

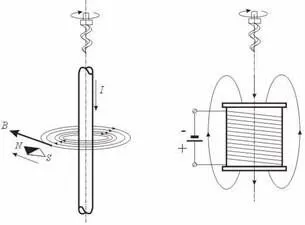
Определим значение напряженности магнитного поля. Поскольку часть магнитного круга представлена ферромагнитными элементами, магнитная индукция для этих элементов может быть определена с помощью графической зависимости магнитной индукции от напряженности магнитного поля

Зависимость индукции от напряженности магнитного поля для электрических и стальных листов.

Поскольку l₁— литой стали, затем в V₁= 1,5 Тесла, напряженность магнитного поля H₁≈ 7 А/см = 700 А/м,

l₂— электросталь, про₂= 1,5 Тесла, напряженность магнитного поля H₂≈ 30 А/см = 3000 А/м,

l₃— воздушного зазора, напряженность магнитного поля определяется следующим образом

где m₀= 4π*1 0-7 — магнитная постоянная,

μ_rB— относительная магнитная проницаемость воздуха, μ_rB≈ 1.

Используя закон полного тока, в котором магнитная индукция выражается напряженностью магнитного поля, мы можем рассчитать число витков провода N

Это дает число витков N = 4083,5.

В дополнение к неразветвленным магнитным цепям часто встречаются разветвленные магнитные цепи, которые показаны на следующей схеме

Схемные модели править

Наиболее распространенным способом представления магнитной цепи является модель сопротивления, которая создает аналогию между электрическими и магнитными цепями. Эта модель хорошо работает для систем, содержащих только магнитные компоненты, но она имеет серьезные недостатки для моделирования системы, содержащей как электрические, так и магнитные части. Он неадекватно моделирует поток тока и энергии между электрической и магнитной областями. Это происходит потому, что электрический резистор высвобождает энергию, в то время как магнитный резистор накапливает ее и высвобождает позже. Альтернативной моделью, которая правильно представляет поток энергии, является модель гиратора-конденсатора.

Модель «сопротивление-сопротивление» для магнитных цепей — это агрегированная модель, в которой электрическое сопротивление пропорционально магнитному сопротивлению.

Закон Ома для магнитных цепей

В электронных схемах, закон Ома представляет собой эмпирическое соотношение между ЭДС прикладывается элемента и тока I он генерирует через этот элемент. Он записывается как: E>>

где R — электрическое сопротивление рассматриваемого материала. Существует аналог закона Ома, используемый в магнитных цепях. Этот закон часто называют законом Джона Хопкинсона, но на самом деле он был сформулирован ранее Генри Огастусом Роуландом в 1873 году. 3 В нем говорится, что 4 5.

где — магнитодвижущая сила (МДС) на магнитном элементе, — магнитный поток, проходящий через магнитный элемент, и — магнитное сопротивление этого элемента. (Позже будет показано, что эта связь обусловлена ​​эмпирической зависимостью между H- полем и магнитным полем B, B = μ H, где μ — проницаемость материала). Подобно закону Ома, закон Гопкинсона можно интерпретировать либо как эмпирическое уравнение, которое работает для некоторых материалов, либо он может служить определением сопротивления. F>>Φ р>>

Закон Хопкинсона не является корректной аналогией закона Ома с точки зрения моделирования потока мощности и энергии. В частности, нет потерь мощности, связанных с магнитным сопротивлением, так же как нет потерь мощности, связанных с электрическим сопротивлением. Магнитное сопротивление, которое в этом отношении является настоящим аналогом электрического сопротивления, определяется как отношение между магнитодвижущей силой и скоростью изменения магнитного потока. Здесь скорость изменения магнитного потока заменяет электрический ток, и аналогия закона Ома становится следующей:

где — магнитное сопротивление. Эта взаимосвязь является частью электромагнетической аналогии, называемой моделью гиратор-конденсатор, и предназначена для преодоления недостатков модели сопротивления. Модель гиратор-конденсатор, в свою очередь, является частью более широкой группы совместимых аналогий, используемых для моделирования систем во многих областях энергии. R m>>

Нежелание

Магнитное сопротивление или импеданс эквивалентно сопротивлению в электрической цепи (хотя магнитная энергия не рассеивается). Подобно тому, как электрическое поле заставляет электрический ток идти по пути наименьшего сопротивления, магнитное поле заставляет магнитный поток идти по пути наименьшего магнитного сопротивления. Это масштабируемая, огромная величина, подобная электрическому сопротивлению.

Полное сопротивление равно отношению между ММФ в пассивной магнитной цепи и магнитным потоком в этой цепи. В поле переменного тока сопротивление равно отношению значений амплитуды синусоидального ММФ и магнитного потока. (см. фазы).

Приложения править

• В сердечниках некоторых трансформаторов могут быть созданы воздушные зазоры, чтобы уменьшить эффекты насыщения. Это увеличивает сопротивление магнитной цепи и позволяет ей накапливать больше энергии до насыщения сердечника. Этот эффект используется в обратноходовых трансформаторах видеодисплеев с электронно-лучевой трубкой и в некоторых типах импульсных источников питания .
• Изменение сопротивления — это принцип, лежащий в основе реактивного двигателя (или генератора переменного сопротивления) и генератора переменного тока Alexanderson .
• Мультимедийныегромкоговорители обычно имеют магнитную защиту, чтобы уменьшить магнитные помехи, вызываемые телевизорами и другими ЭЛТ. Магнит динамика покрыт таким материалом, как мягкое железо, чтобы минимизировать паразитное магнитное поле.

Сопротивление также может быть применено к датчикам с переменным сопротивлением (магнитные датчики).

См. Также править

1. ^ Международная электротехническая комиссия
2. ^ Мэтью М. Радманеш, Врата к пониманию: электроны к волнам и за его пределами, стр. 539, AuthorHouse, 2005 ISBN1418487406 .
3. ^ Роуленд Х., Фил. Mag. (4), т. 46, 1873, стр. 140.
4. ^ Магнетизм (вспышка)
5. ^ Тещ, Фредрик; Мишель Яноз; Торбьорн Карлссон (1997). Методы анализа ЭМС и расчетные модели. Wiley-IEEE. п. 513. ISBN0-471-15573-X .

• Магнитно-электрические аналоги Денниса Л. Фойхта, Innovatia Laboratories (PDF). Архивировано 17 июля 2012 г., в Wayback Machine.
• Интерактивное руководство Java по магнитным шунтам Национальная лаборатория сильных магнитных полей

Приложения

• В сердечниках некоторых трансформаторов могут быть созданы воздушные зазоры, чтобы уменьшить воздействие насыщенность. Это увеличивает сопротивление магнитной цепи и позволяет ей хранить больше энергия до насыщения сердечника. Этот эффект используется в обратноходовые трансформаторы видеодисплеев с электронно-лучевой трубкой и в некоторых типах импульсный источник питания.
• Изменение сопротивления — это принцип, лежащий в основе реактивный двигатель (или генератор переменного сопротивления) и Генератор Alexanderson.
• Мультимедиамузыкальные колонки обычно имеют магнитную защиту, чтобы уменьшить магнитные помехи, вызываемые телевизоры и другие ЭЛТ. Магнит динамика покрыт таким материалом, как мягкое железо для минимизации паразитного магнитного поля.

Резистор также можно использовать для магнитных динамиков с переменным импедансом.

См. Также

1. ^Международная электротехническая комиссия
2. ^Мэтью М. Радманеш, Путь к пониманию: электроны к волнам и за его пределами, стр. 539, AuthorHouse, 2005 ISBN1418487406.
3. ^Роуленд Х., Фил. Mag. (4), т. 46, 1873, стр. 140.
4. ^Магнетизм (вспышка)
5. ^Теш, Фредерик; Мишель Яноз; Торбьорн Карлссон (1997). Методы анализа ЭМС и расчетные модели. Wiley-IEEE. п. 513. ISBN0-471-15573-X.

• Магнитно-электрические аналоги Деннис Л. Фейхт, Innovatia Laboratories (PDF) Архивировано 17 июля 2012 г., на Wayback Machine
• Интерактивное учебное пособие по Java по магнитным шунтам Национальная лаборатория сильных магнитных полей

Различные электромагнитные механизмы широко используются в технике. Некоторые из них преобразуют электрическую энергию в механическую (электродвигатели, реле, электроизмерительные механизмы), другие генерируют магнитные поля с нужными свойствами. Магнитная цепь — это сочетание магнитной катушки, которая образует замкнутый контур для магнитного потока, и элементов, создающих магнитное поле (токоведущие обмотки, постоянные магниты). Задача магнитной цепи — генерировать магнитное поле нужной силы, конфигурации и направления в рабочей зоне электрического устройства.

При анализе магнитных цепей необходимо различать путь магнитного потока Ф и путь потока утечки Ф_dкоторые образуются магнитными линиями вне ферромагнитного материала. Важно понимать конфигурацию магнитного поля в рабочем контуре (пороговое поле). Классификация магнитных цепей Магнитные цепи могут быть как однородными (все магнитопроводы состоят из одного и того же ферромагнитного материала), так и неоднородными (например, с воздушным зазором). Магнитные цепи могут быть разветвленными или неразветвленными, симметричными или асимметричными. Закон Ома для магнитной цепи Рассмотрим магнитную цепь, состоящую из катушки, намотанной кольцом вокруг магнитопровода (тороида). Когда в катушке течет ток I, в магнитной цепи индуцируется магнитное поле, которое сосредоточено в объеме кольца (без паразитного поля). Выбирается контур интегрирования в виде круга радиусом R и применяется закон полного тока: — линейный интеграл вектора интенсивности по замкнутому контуру равен алгебраической сумме токов, определяемых этим контуром; — полный ток (I_{общий ток}Для практических целей наиболее интересен случай, когда контур интегрирования проходит через обмотку с числом витков w и током I._{мы пишем}

Сумма токов wI через область, ограниченную контуром интегрирования, называется магнитодвижущей силой F, F = wI. Если предположить, что угол между векторами H и dl равен нулю, а значение H одинаково в каждой точке контура интегрирования, то определяется среднее значение напряженности магнитного поля, поскольку H не зависит от магнитных свойств магнитной цепи, а прямо пропорционально току в обмотке. Точнее, он равен МП обмотки на единицу длины средней токопроводности магнитной цепи. Из соотношений F = B S и B = m_aH получаем F = μ_aH S = μ_aS(I w / l) = I w / ( l / μ_aS) = F/R_м. Это выражение называется законом Ома для магнитной цепи. Поэтому значение R_м= l / μ_aS называется магнитным сопротивлением магнитной цепи (аналогично электрическому сопротивлению). При анализе магнитных цепей разность магнитных потенциалов между двумя магнитными точками называется разностью магнитных потенциалов, которая равна магнитному напряжению U_мabU_мab= H l_ab.

Расчет неразветвленной магнитной цепи постоянного тока

Формула, выражающая закон полного тока магнитной цепи, была выведена для кольцеобразной магнитной цепи с фиксированным поперечным сечением и равномерно распределенными обмотками. Формула была распространена на магнитные цепи, в которых намагничивающая катушка расположена в ограниченной области магнитной цепи, а отдельные контуры состоят из различных ферромагнитных и неферромагнитных материалов с различными сечениями. В приближенных расчетах магнитных цепей предполагается, что магнитный поток остается одинаковым во всех областях цепи, хотя в действительности магнитная цепь также содержит поток утечки Ф_ркоторые заключены в воздухе и не следуют по пути магнитной цепи. При вычислении магнитных кругов различают прямые и обратные задачи.

1. Прямая задача

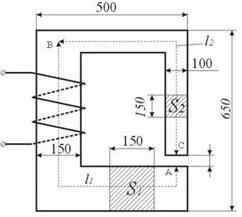
Требуется: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H) (кривая намагничивания) ферромагнитных материалов, из которых состоит магнитная цепь; 3) магнитный поток Ф, который должен быть создан в магнитной цепи. Требуется найти магнитную силу F = IW. Решение задачи рассматривается применительно к магнитной цепи, показанной на рисунке 10. Рисунок 10. Магнитная цепь 1 Магнитная цепь разделена на ряд сегментов одинакового сечения S из однородного материала. 2 Зарисован ход средней магнитной линии (пунктирная линия на рисунке). 3. поскольку магнитный поток постоянен на всех участках контура, магнитная индукция B = F/S на каждом участке и напряженность магнитного поля H постоянны. Это позволяет относительно легко определить величину. Напишем интеграл от. где.₁и L₂— длины ферромагнитных участков цепи в м. d — ширина воздушного зазора в м. 4.₁и H₂определяются по известным значениям магнитной индукции B с использованием кривых намагничивания для ферромагнитных материалов. А для воздушного зазора F получаем: — магнитное сопротивление расстояния 1, — магнитное сопротивление воздушного зазора. Перепишем выражение (*) в терминах определителей: (**) Последнее выражение, т.е. зависимость магнитного потока от магнитодвижущей силы ( wI ) и магнитных сопротивлений участков магнитной цепи, называется основным законом магнитной цепи. Аналогия между (**) и законом Ома для полной цепи хорошо видна:

Магнитные величины	Магнитные величины
Имя	Имя	Единица измерения	Имя	Имя	Единица измерения
Магнитный поток	Ф	Вб	Текущий поток	I	A
Магнитная сила	wI	A	Электродвижущая сила	Е	В
Магнитное сопротивление	RM		Электрическое сопротивление	R	Ом
Магнитное напряжение	UM=RMF = H l	А	Электрическое напряжение	U=RI	B

Используя соотношения, мы можем нарисовать схему магнитной цепи, представленной ранее. Полученная схема содержит последовательно соединенные нелинейные элементы R_M1и Р_M2. Их нелинейность зависит от напряженности магнитного поля H или силы тока в катушке I, т.е. от действующего в цепи МФД.

Магнитные цепи электротехнических устройств переменного тока

Рассмотрим электромагнитное состояние устройства, состоящего из магнитопровода и намагничивающей катушки, подключенных к источнику синусоидального напряжения.

Под воздействием приложенного напряжения u возникает ток i, который индуцирует изменяющийся магнитный поток F_t. В упрощенном анализе мы пренебрегаем паразитными полями F_d.

Поток F_tвызывает ЭДС самоиндукции i в обмотках катушки. Поскольку обмотка имеет электрическое сопротивление R_Кможно написать электрическое уравнение состояния для диаграммы удушения на рисунке:

Без учета сопротивления обмотки (R_К=0), можно записать:

Предположим, что входное напряжение колеблется по закону

Решив последнее уравнение, мы можем определить закон магнитного потока:

амплитудное значение магнитного потока.

Отсюда следует, что амплитуда магнитного потока определяется частотой U_mПри увеличении частоты переменного тока амплитуда магнитного потока соответственно уменьшается, и чем меньше магнитный поток, тем меньше магнитная цепь трансформатора переменного тока. По этой причине источники питания современной компактной электроники и многих других устройств, например, так называемые сварочные инверторные трансформаторы, используют преобразование из частоты 50 Гц в переменный ток на несколько порядков выше.

Амплитуда магнитного потока не зависит от вида и свойств B ( H ) магнитной цепи и намагничивающего тока i .

Нарисуем значения F_t, u 1 и e_Ркак векторы на векторной диаграмме:

Обратите внимание, что вектор потока F_mлежит на 90° позади вектора напряжения U 1 .

Если к обмотке идеальной индукционной катушки с магнитопроводом приложить синусоидальное напряжение, то в магнитопроводе возникает магнитный поток, который также колеблется синусоидально, но отстает от напряжения на 90°.