Из анализа формул для тангенциального и нормального ускорения можно сделать вывод, что тангенциальное ускорение характеризует изменение скорости только по величине, а нормальное — только по n-направлению.
Мгновенная скорость
При рассмотрении неравномерного движения нас часто интересует не средняя скорость тела, а скорость в определенный момент времени или мгновенная скорость. Например, когда тело ударяется о препятствие, сила, которую тело оказывает на препятствие в момент удара, определяется скоростью в момент удара, а не средней скоростью тела. Форма траектории снаряда и радиус его движения зависят от скорости в момент запуска, а не от средней скорости.
Средняя скорость ($\левый угол v\правый угол $) материальной точки на оси x равна
\left\angle v
ight\angle =\left\angle(1
ight),\
$\Delta t$ — временной интервал движения тела.
Мгновенная скорость определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени:
Мгновенная скорость равномерного движения материальной точки
Этот предел в математике называется производной:
Выражение (3) гласит, что мгновенная скорость (скорость в данный момент времени) является производной от координаты. Для прямолинейного движения материальной точки мгновенная скорость может быть определена как производная расстояния ($s$) по времени:
Средняя скорость равномерно движущейся точки постоянна, поэтому мгновенная скорость равномерно движущейся точки — величина постоянная.
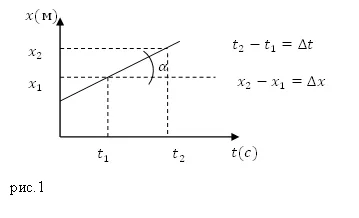
Скорость равномерного движения численно равна тангенсу наклона линии на оси времени (рис. 1):
\v=k\ tg\ \alpha\ \ \ \links(4
Мгновенная скорость при криволинейном движении
ight),\
где $k$ — безразмерный коэффициент, определяющий соотношение между единицами перемещения (ось линии) и единицами времени (ось ножки).
Описание криволинейного движения
В графическом представлении переменного движения материальной точки мгновенная скорость численно равна углу наклона касательной линии к графику и оси пропасти.

Положение материальной точки на графике задается радиус-вектором $\overline(t)$, проведенным из фиксированной точки, которая является началом координат, в точку наблюдения. Тогда мгновенная скорость материальной точки — это векторная величина, равная:
скорость — это вектор, направленный по касательной к траектории материальной точки в положении частицы.
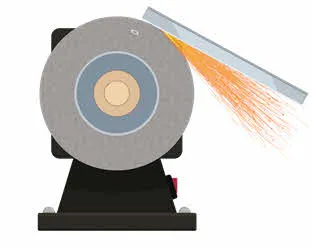
Движение, траектория которого не является прямолинейной, называется криволинейным движением. Примерами криволинейного движения являются вращение частей машины, колеса, движение листьев на ветру, полет камня, брошенного под углом к горизонту, и многие другие.
Скорость при криволинейном движении
Криволинейное движение — это гораздо более сложное движение по сравнению с прямолинейным. При прямолинейном движении коэффициенты векторов перемещения, скорости и ускорения изменяются. Их направления всегда параллельны вектору перемещения. Если движение криволинейное, то меняются не только модули, но и направления. На самом деле, изменения в направлении векторов перемещения и скорости являются наиболее важными признаками криволинейного движения.
Первый метод изучения криволинейного движения — это проецирование его на координатные оси. Спроектированное движение является прямолинейным, и к нему можно применить законы прямолинейного движения.
Второй метод — разделить весь путь на небольшие отрезки, каждый из которых аппроксимирует прямолинейное движение неограниченно, так что становится возможным использовать формулы для прямолинейного движения как формулы для криволинейного движения.
Перемещение — это вектор от начала траектории до ее конца. При линейном движении этот вектор также является траекторией движения, а направление вектора скорости совпадает с направлением вектора перемещения.

Ускорение при криволинейном движении
При криволинейном движении траектория больше, чем вектор перемещения. Однако чем меньше вектор смещения, тем меньше разница.
Поэтому если разделить траекторию на множество маленьких сегментов, то движение на каждом из них будет очень близко к прямой линии. Направление скорости в каждом сегменте совпадает с направлением сегмента. По мере увеличения числа этих отрезков каждый из них неограниченно сходится к точке, направление которой параллельно касательной к этой точке.
Таким образом, мгновенная скорость криволинейного движения направлена по касательной к траектории движения.
Прямолинейное и криволинейное движение. РД тела по окружности

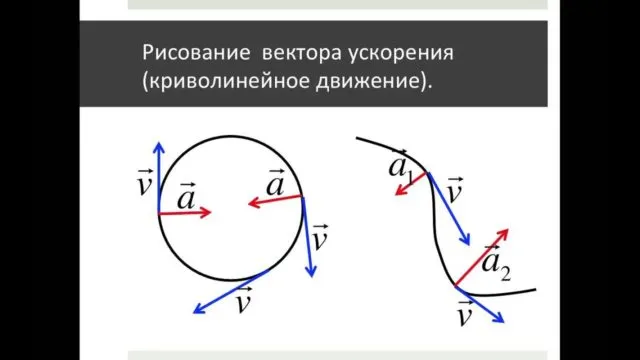
Ускорение — это мера изменения скорости. И если скорость линейного движения постоянна, то ускорение также равно нулю. При криволинейном движении скорость постоянно меняется. Мера вектора скорости может оставаться постоянной, но поскольку вектор всегда направлен по касательной к траектории, которая не является прямой линией, направление этого вектора постоянно меняется. И если вектор скорости постоянно меняется (даже если он меняется не по модулю, а только по направлению), это означает, что ускорение всегда присутствует в таком движении.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Если бы направление вектора скорости и вектора ускорения было одинаковым в один момент, то скорость изменила бы свой модуль только в следующий момент, ее направление осталось бы прежним, путь стал бы прямой линией, движение стало бы прямолинейным.

Криволинейное движение — это всегда движение с ускорением. И направление вектора ускорения никогда не совпадает с направлением вектора скорости.
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Прямолинейное и криволинейное движение. РД тела по окружности»
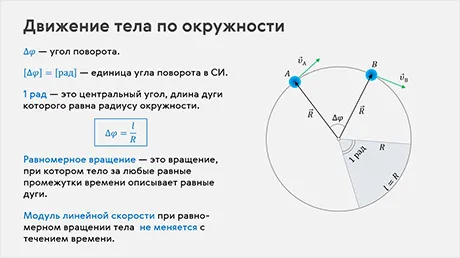
В этом видеоуроке мы поговорим о криволинейном движении тел и узнаем, что его вызывает. Рассмотрим простейшую форму криволинейного движения — круговое движение тела. Мы также рассмотрим основные характеристики этого типа движения и научимся его определять.
Чтобы получить доступ к этим и другим видеоурокам, вам необходимо добавить их в свой личный шкафчик.
2. Распространите видеоуроки в своих личных кабинетах среди учеников.
В предыдущем уроке мы говорили о том, что любое тело находится в состоянии покоя или равномерного прямолинейного движения, пока к нему не приложена сила. Другими словами, действие силы необходимо не для поддержания постоянной скорости тела, а для ее изменения. Сила может изменить как меру скорости, так и ее направление.
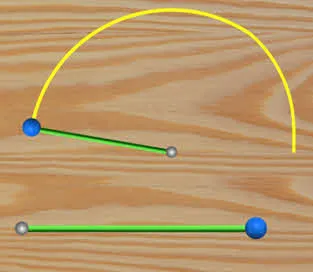
На экране вы видите мяч, прикрепленный к столу резиновой струной. Когда мы перемещаем шарик на определенное расстояние, струна растягивается, и на нее действует сила упругости. Дайте мячу двигаться. Под действием сил упругости он приходит в ускоренное движение и перемещается в исходное положение. Скорость шарика в любой точке траектории совпадает с направлением действующей на него силы и, следовательно, с направлением вектора ускорения. Следовательно, в этом движении изменяется только численное значение скорости, а направление ее вектора остается неизменным, и мяч движется по прямой.
Давайте повторим эксперимент. Однако теперь шарик не двигают, а толкают, в результате чего он приобретает начальную скорость, перпендикулярную проволоке.

Если бы на шарик не действовали никакие силы, он бы сохранил меру и направление результирующей скорости в соответствии с законом инерции. Но при движении наш шарик отходит от точки крепления шнура и немного растягивает сам шнур. Это создает упругую силу в шнуре, которая пытается вернуть его к первоначальной длине и одновременно приближает шарик к точке крепления шнура. В результате действия силы направление скорости шарика меняется в каждый момент времени, и шарик движется по искривленной траектории. В любой точке траектории скорость направлена по касательной, а сила направлена к точке крепления струны.
Ускорение при криволинейном движении
При криволинейном движении траектория больше, чем вектор перемещения. Однако чем меньше вектор смещения, тем меньше разница.
Поэтому если разделить траекторию на множество маленьких сегментов, то движение на каждом из них будет очень близко к прямой линии. Направление скорости в каждом сегменте совпадает с направлением сегмента. По мере увеличения числа этих отрезков каждый из них неограниченно сходится к точке, направление которой параллельно касательной к этой точке.
Таким образом, мгновенная скорость криволинейного движения направлена по касательной к траектории движения.
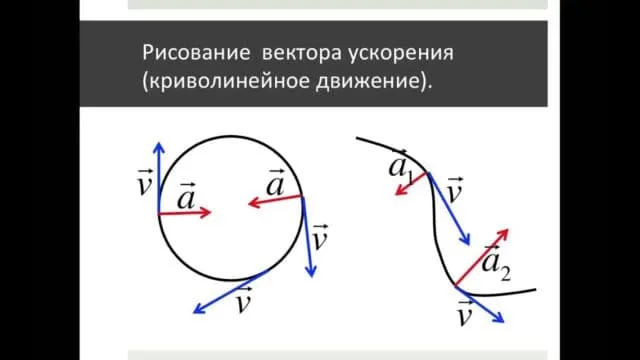
Ускорение — это мера изменения скорости. А если скорость линейного движения постоянна, то ускорение равно нулю. При криволинейном движении скорость постоянно меняется. Мера вектора скорости может оставаться постоянной, но поскольку вектор всегда направлен по касательной к траектории, которая не является прямой линией, направление этого вектора постоянно меняется. И если вектор скорости постоянно меняется (даже если он меняется не по модулю, а только по направлению), это означает, что ускорение всегда присутствует в таком движении.








