Катушка индуктивности. Описание, характеристики, формула расчета. Максимальная сила тока протекающего через катушку формула.

Содержание

Пример 3. Свободные электромагнитные колебания возникают в двух идеальных колебательных контурах с одинаковой индуктивностью, с периодом колебаний 9⋅10-8 с в первом контуре и 3⋅10-8 с во втором. Во сколько раз значение амплитуды тока во второй цепи больше, чем в первой, если максимальный заряд конденсатора в обоих случаях одинаков?

Максимальная энергия магнитного поля катушки индуктивности формула

Когда в эксперименте цепь размыкалась (см. рис. 150, в), лампа ярко вспыхивала. Откуда взялась энергия, которая заставила лампу гореть в данном случае? Поскольку это происходило при отключении цепи от источника питания, т.е. при уменьшении индукции магнитного поля катушки, энергия, потребляемая лампой, сохранялась в виде энергии магнитного поля. При размыкании цепи он начинает исчезать, а накопленная в нем энергия преобразуется в электрическую энергию путем самоиндукции, которая включает лампу. Результат: магнитное поле обладает энергией.

Запас энергии магнитного поля катушки соответствует энергии, потребляемой источником тока при превышении напряжения самоиндукции с течением времени, в то время как сила тока возрастает от нуля до определенного значения I при замыкании цепи (см. рисунок 150, б). Часть работы эффекта источника в катушке используется для нагрева проводников, другая часть, которая соответствует среднеквадратичному значению самоиндукции E_это= Е_сэто работа, совершаемая катушкой против автопилота, напр.

Работа, совершаемая током для преодоления напряжения самоиндукции, равна энергии магнитного поля катушки:

Ток изменился от 0 до I, поэтому изменение тока равно ΔI = I. Следовательно,

Давайте заменим E_си я_срв формуле (3):

Получаем формулу для энергии магнитного поля катушки.

Зависимость энергии магнитного поля катушки от ее индуктивности и от силы тока можно увидеть в следующем эксперименте. Увеличьте ток катушки с помощью реостата и разомкните цепь. В этом случае лампа мигает ярче, чем при низком токе катушки. Поэтому чем больше ток в катушке, тем больше энергия магнитного поля катушки. Удалите половину сердечника из катушки и тем самым уменьшите индуктивность. Установите ток в цепи на то же значение, а затем включите ее. В этом случае лампа мигает менее ярко. Чем больше индуктивность катушки, тем больше магнитная энергия катушки. Энергия магнитного поля используется, например, в электромагнитном кране для притягивания железных деталей к электромагнитному сердечнику крана и, таким образом, генерирования тока во вторичной обмотке трансформатора.

Задача 36. В катушке без сердечника ток увеличился с 1 до 2 А за 0,01 секунды, а энергия индукции в катушке составила 20 В. Определите индуктивность катушки и изменение энергии ее магнитного поля.

Изменение энергии магнитного поля катушки составляет

Если в цепи с индуктивностью L течет ток I, то возникает индукционный ток и совершается работа при размыкании цепи. Эта работа совершается за счет энергии магнитного поля, которая исчезла при размыкании цепи. Вследствие закона сохранения и закона преобразования энергия магнитного поля в основном преобразуется в энергию электрического поля, которая нагревает проводники. Произведение можно определить из следующей зависимости

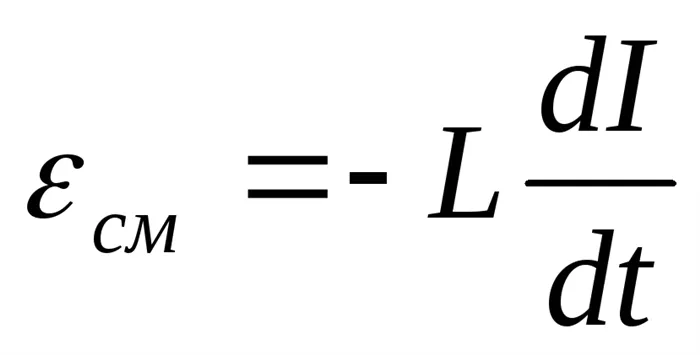
Поскольку, то

Уменьшение энергии магнитного поля равно работе тока, поэтому

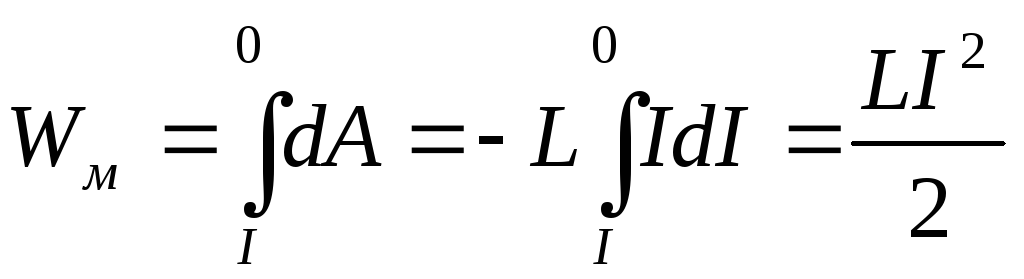
(16.18)

Формула применима к любой цепи и показывает, что энергия магнитного поля зависит от индуктивности цепи и протекающего через нее тока.

Примеры решения задач

Пример. В магнитном поле, которое, согласно закону B=B cosωt (B =5мТл,

ω=5с-1 ), прикреплена круглая проволочная катушка радиуса r=30см, причем перпендикуляр к катушке образует угол α=30º с направлением поля. Определите индуктивную ЭДС, развиваемую в катушке в момент времени t=10с.

Дано.

Решение: в соответствии с законом Фарадея,

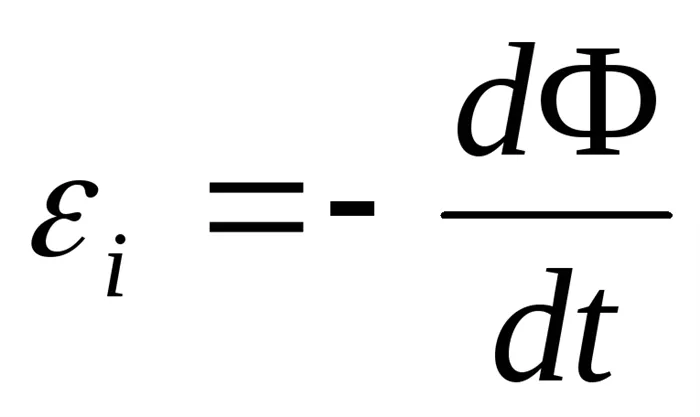
, (1)

где — магнитный поток, связанный с катушкой в любом положении относительно магнитного поля.

По условию задачи B=B cosωt и площадь кольца S=πr 2, следовательно, имеет место.

Подставив выражение (2) в формулу (1) и изменив ее, мы получим требуемую индуктивную ЭЭД в данный момент времени:

Пример В катушке соленоида длиной ℓ=50см и диаметром d=6см ток равномерно увеличивается на 0,3А за одну секунду. Определите число витков катушки соленоида, если индукционный ток в кольце из медной проволоки радиусом 3,1 см (ρ=17 нОм∙м), лежащем на катушке, равен I_к=0,3 А.

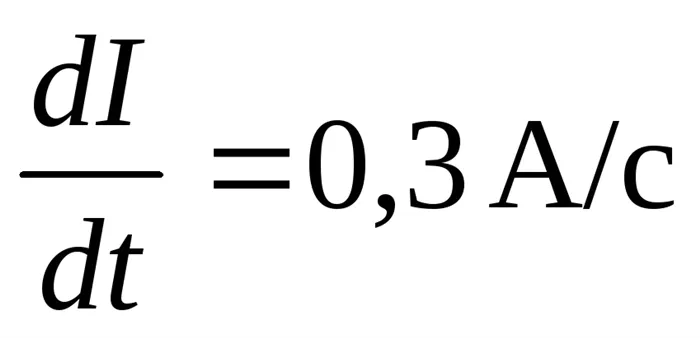
Дано: ℓ=50см=0,5м; d=6см=0,06м; ;r_к=3,1см=3,1∙1 0-2 м; ρ=17нОм∙м=17∙1 0-9 Ом∙м; I_к=0,3 А.

Решение. ЭДС самоиндукции возникает в катушке соленоида при изменении тока.

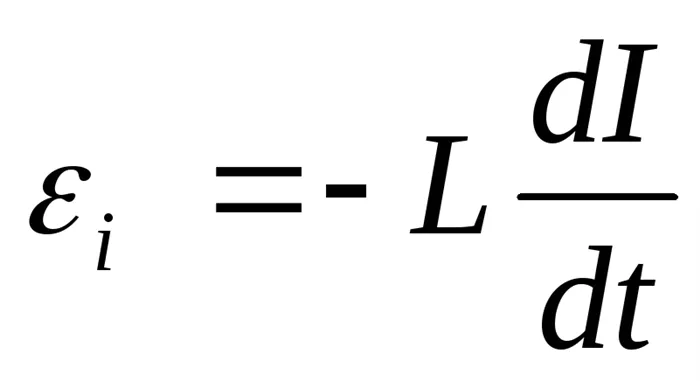
(1)

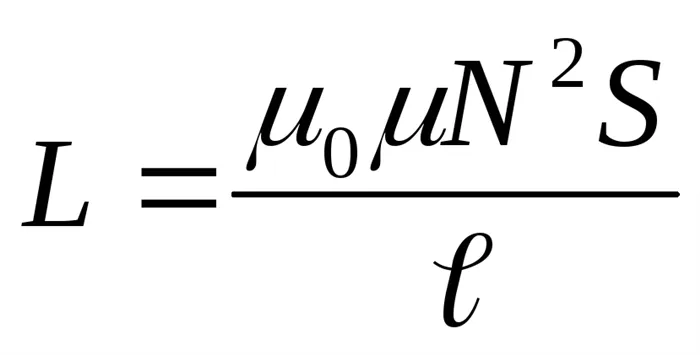
где — индуктивность катушки соленоида. Если подставить это выражение в (1)

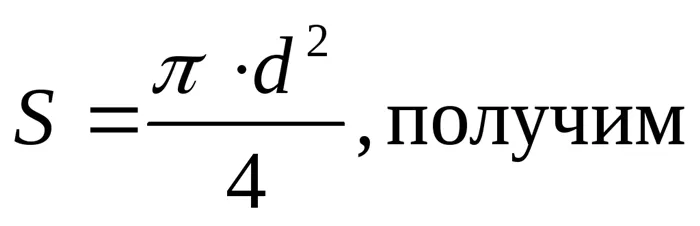
принимая во внимание

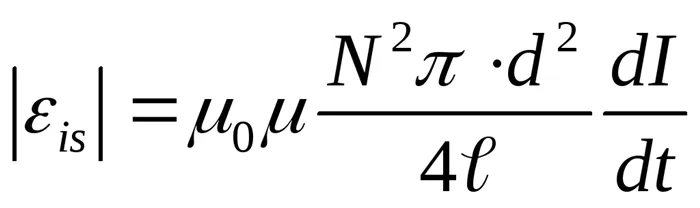
ЭЭД индуктивности, возникающей в кольце, в N раз меньше определенного значения ЭЭД индуктивности в катушке с N витками, т.е.

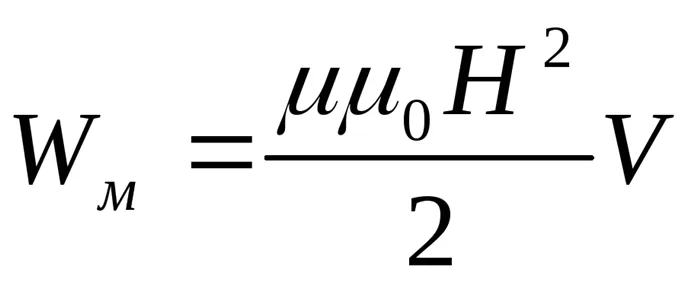
. (2)

Согласно закону Ома, индукционный ток в кольце равен

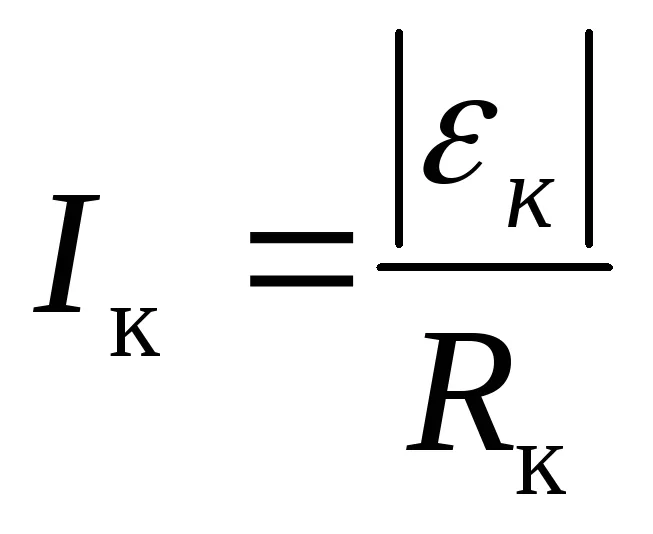
, (3)

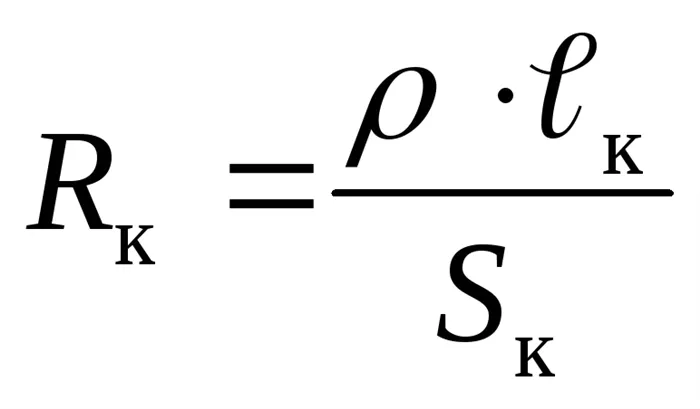
где — сопротивление кольца. Поскольку ℓ_к=πd и S_к=πr_к2, выражение (3) имеет вид

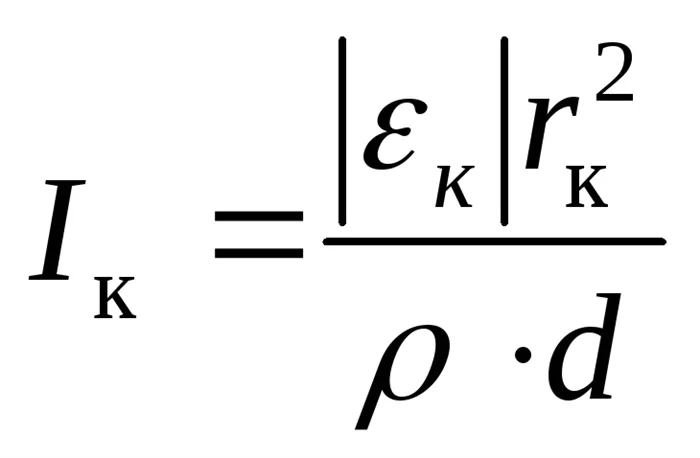
Подставив выражение (2) в эту формулу, получим желаемое количество витков трубки

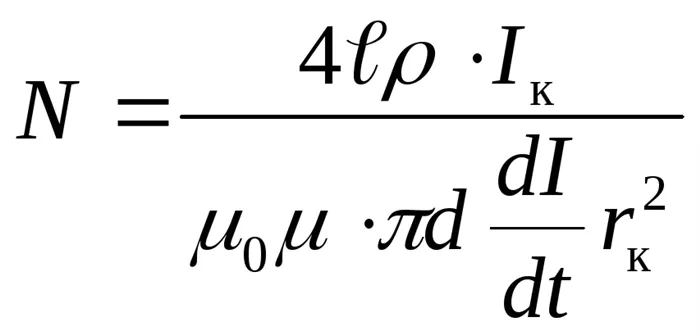
Пример В однородном магнитном поле подвижная сторона (длина ℓ = 20 см) прямоугольной рамки (см. рисунок) движется перпендикулярно линиям магнитной индукции со скоростью u = 5 м/с. Определите индукцию B магнитного поля, когда индуктивная ЭДС e_i=0,2 В.

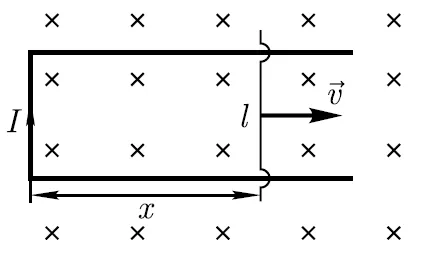
Решение. По мере того как движущаяся сторона рамки перемещается через магнитное поле, поток Ф вектора магнитной индукции через рамку увеличивается, что соответствует закону Фарадея,

Почему возникает магнитное поле

Магнитные свойства некоторых веществ, которые притягивают металлические предметы, известны давно. Но понять природу этого явления удалось лишь в начале девятнадцатого века. По аналогии с электрическими зарядами были предприняты попытки объяснить магнитные явления в терминах определенных магнитных зарядов (диполей). В 1820 году датский физик Ганс Эрстед обнаружил, что магнитная стрелка отклоняется, когда через расположенный рядом проводник проходит электрический ток.

В то же время французский исследователь Андре Ампер обнаружил, что два проводника, расположенные параллельно друг другу, притягиваются друг к другу, когда электрический ток течет через них в одном направлении, и отталкиваются друг от друга, когда токи текут в разных направлениях.

Рисунок 1: Эксперимент Бернштейна с проводами и током. Игла компаса возле токоведущего провода.

На основании этих наблюдений Эмбер сделал вывод, что взаимодействие тока со стрелкой, притяжение (и отталкивание) проводов и постоянных магнитов можно объяснить, исходя из предположения, что магнитное поле создается движущимися электрическими зарядами. Кроме того, Бернштейн выдвинул смелую гипотезу, что внутри вещества существуют незатухающие молекулярные токи, которые и являются причиной постоянного магнитного поля. Тогда все магнитные явления можно объяснить взаимодействием движущихся электрических зарядов, а особых магнитных зарядов не существует.

Математическая модель (теория), позволившая рассчитать величину магнитного поля и силы взаимодействия, была разработана английским физиком Джеймсом Максвеллом. Из уравнений Максвелла, связывающих электрические и магнитные явления, следует, что:

Магнитное поле возникает только в результате движения электрических зарядов;
Постоянное магнитное поле существует у природных магнитных тел, но и в этом случае причиной возникновения поля является непрерывное движение молекулярных токов (вихрей) в массе вещества;
Магнитное поле можно создать еще с помощью переменного электрического поля, но это тема будет рассмотрена в следующих наших статьях.

Накопленная энергия в индуктивности

Как мы знаем, магнитное поле обладает энергией. Подобно тому, как электрическая энергия хранится в полностью заряженном конденсаторе, она хранится и в индукционной катушке, по обмоткам которой течет ток — только на этот раз это магнитная энергия.

Энергия, запасенная в катушке индуктивности, соответствует энергии, необходимой для обеспечения протекания тока I, чтобы справиться с HED. Количество энергии, запасенной в катушке, можно рассчитать по следующей формуле:

Где L — индуктивность, а I — ток, протекающий через катушку индуктора.

Гидравлическая модель

Работу индукционной катушки можно сравнить с работой водяной турбины в потоке воды. Поток воды через турбину, которая еще не раскручена, будет испытывать сопротивление до тех пор, пока турбина не раскрутится полностью.

Турбина, обладающая определенной степенью инерции, будет вращаться в устойчивом потоке, практически не влияя на поток воды. Однако если этот поток резко прерывается, турбина продолжает вращаться благодаря своей инерции и создает движение воды. И чем больше инерция этой турбины, тем больше она будет сопротивляться изменению потока.

Аналогично, индукционная катушка сопротивляется изменениям тока, протекающего через нее.

Индуктивность в электрических цепях

В то время как конденсатор сопротивляется изменению переменного напряжения, индуктор сопротивляется переменному току. Идеальный индуктор не оказывает сопротивления постоянному току, но в действительности все индукторы оказывают некоторое сопротивление.

Многофункциональный прибор для тестирования транзисторов, диодов и тиристоров.

В общем случае, связь между изменяющимся во времени напряжением V(t), протекающим через индуктор индуктивностью L, и изменяющимся во времени током I(t), протекающим через него, может быть представлена в виде дифференциального уравнения следующей формы:

Когда синусоидальный переменный ток (AC) проходит через индуктор, генерируется синусоидальное переменное напряжение (SAV). Амплитуда SAV зависит от амплитуды тока и частоты синусоиды, что может быть выражено следующим уравнением:

Где ω — угловая частота резонансной частоты F:

Кроме того, фаза тока на 90 градусов ниже фазы напряжения. Для конденсатора верно обратное: ток опережает напряжение на 90 градусов. При подключении индуктора к конденсатору (последовательно или параллельно) образуется LC-контур, работающий на определенной резонансной частоте.

Индуктивное сопротивление XL определяется по формуле:

Где XL — индуктивность, ω — угловая частота, F — частота в герцах, L — индуктивность в генах.

Индуктивное сопротивление — это положительная составляющая импеданса. Она измеряется в Ω. Сопротивление катушки индуктивности (индуктивность) рассчитывается по следующей формуле:

Конденсатор, катушка и резонанс в цепи переменного тока

Опишем колебания, возникающие в цепи переменного тока при включении в цепь конденсатора и индуктора. Давайте также рассмотрим условия, при которых возникает резонанс в цепи переменного тока. Мы выведем формулы для расчета ширины напряжения, введем понятия емкости и индуктивности и узнаем, какую роль играют эти величины.

Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).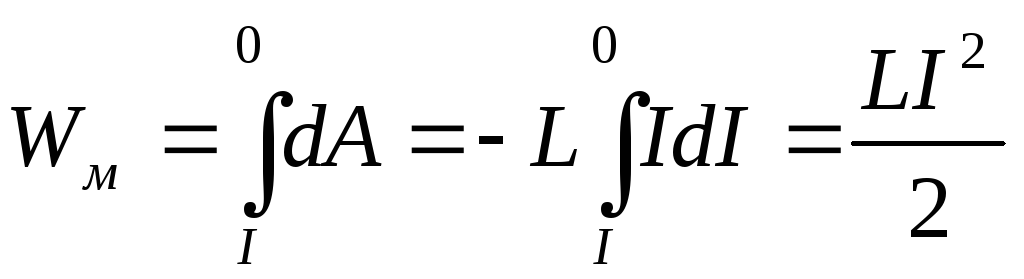Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться. колебания силы тока опережают колебания напряжения на конденсаторе на π 2. . (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.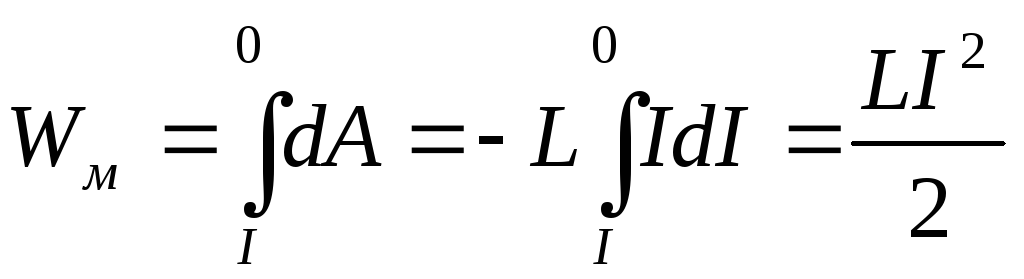Амплитуда силы тока равна: I m a x = U m a x C ω Примем, что: 1 C ω. . = X C Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что: Определение I = U X C. . Величина X C, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть. Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура q m a x = 10 − 6 Кл. Амплитудное значение силы тока в контуре I m a x = 10 − 3 А. Определите период колебания (потерями на нагревание проводника пренебречь). Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки: q 2 m a x 2 C. . = L I 2 m a x 2. . Отсюда: L C = q 2 m a x I 2 m a x. . √ L C = q m a x I m a x. . T = 2 π √ L C = 2 π q m a x I m a x. . = 2 · 3, 14 10 − 6 10 − 3. . ≈ 6, 3 · 10 − 3 ( с )

Катушка индуктивности в цепи переменного тока

Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).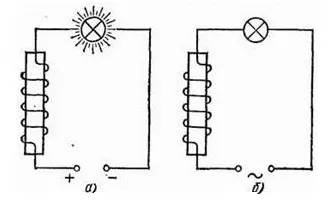Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока. Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока. Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.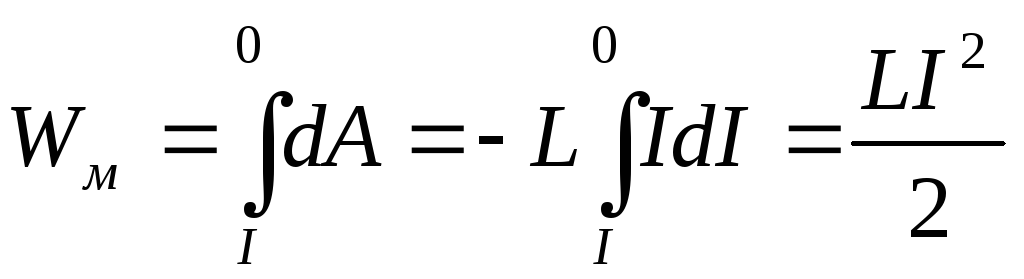Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля → E i, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля → E к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи. Из равенства → E i = − → E к следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции e i ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать: e i = − u Напомним, что сила переменного тока изменяется по гармоническому закону: i = I m a x sin. ω t Тогда ЭДС самоиндукции равна: e i = − L i ´ = − L ω I m a x cos. ω t Так как u = − e i, то напряжение на концах катушки оказывается равным: u = L ω I m a x cos. ω t = L ω I m a x sin. ( ω t + π 2. . ) = U m a x ( ω t + π 2. . ) Амплитуда напряжения равна: U m a x = L ω I m a x Следовательно, колебания напряжения на катушке опережают колебания силы тока на π 2. ., или колебания силы тока отстают от колебаний напряжения на π 2. ., что одно и то же. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).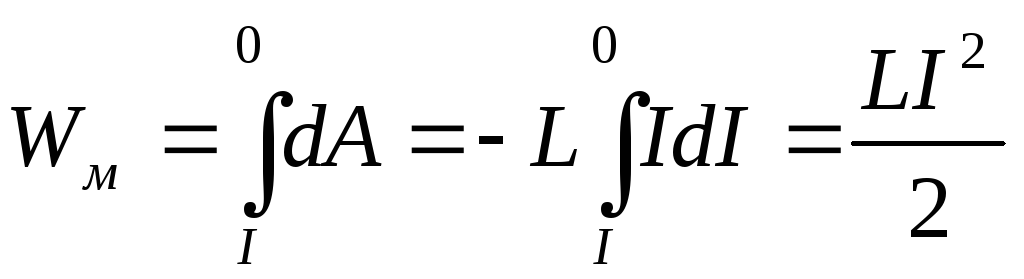Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна: I m a x = U m a x L ω. . Введем обозначение: L ω = X L Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим: Определение I = U X L. . Величина X L

Резонанс в электрической цепи

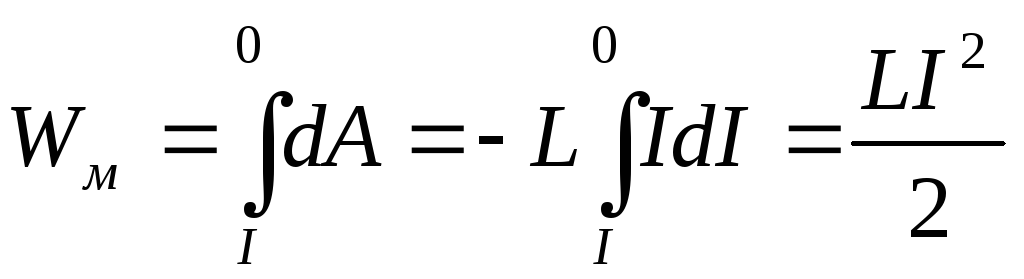
Механические и электромагнитные колебания по своей сути различны, но процессы, в них участвующие, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как и резонанс в колебательной системе, подверженной действию периодической силы. Напомним, что в механической системе, чем меньше трение между элементами колебательной системы, тем сильнее выражен резонанс. Роль трения в электрической цепи играет активное сопротивление R. Наличие этого резистора в цепи приводит к преобразованию энергии тока во внутреннюю энергию проводника, который при этом нагревается. Поэтому резонанс в цепи отчетливо проявляется, когда активное сопротивление R мало. Когда активное сопротивление мало, собственная частота в резонансном контуре определяется следующей формулой: ω 0 = 1 √ L C. Сила тока вынужденного колебательного тока должна достигать максимальных значений, когда частота переменного напряжения, приложенного к цепи, равна собственной частоте колебательного контура: ω = ω 0 = 1 √ L C. Определение Резонанс в электрическом колебательном контуре — это явление резкого увеличения амплитуды вынужденных колебаний тока, когда частота внешнего переменного напряжения равна собственной частоте колебательного контура. При подаче внешнего переменного напряжения резонансное значение тока в цепи достигается не сразу, а постепенно. Амплитуда колебательного тока увеличивается до тех пор, пока энергия, выделяемая резистором за период, не сравняется с энергией, выделяемой в цепи за тот же период: I 2 m a x R 2. = U m a x I m a x I m a x 2 …. Упрощая это уравнение, получаем I m a x R = U m a x Следовательно, амплитуда установившихся колебаний тока при резонансе определяется следующим уравнением: I m a x = U m a x R. Если сопротивление стремится к нулю, ток возрастает до бесконечно большого значения. Если сопротивление велико, ток увеличивается незначительно. Это наглядно показано на диаграмме ниже. Пример 3: Цепь переменного тока с частотой n = 500 Гц содержит катушку с индуктивностью L = 10 мГн. Какова емкость конденсатора, который должен находиться в этой цепи, чтобы возник резонанс? Схема, описанная в условии, является резонансной схемой. Резонанс в контуре достигается, когда частота переменного тока равна собственной частоте колебательного контура (n = n₀). Но: ν 0 = 1 2 π √ L C. Тогда: ν = 1 2 π √ L C. Следовательно:

Задача EF22579 Источник тока подключен к колебательному контуру, к клеммам которого приложено напряжение, гармонически изменяющееся с частотой n. Индуктивность L дроссельной катушки колебательного контура может постепенно увеличиваться от максимального значения L_maxдо минимального значения L_minа емкость его конденсатора постоянна. Студент постепенно уменьшал индуктивность индуктора от максимального до минимального значения и обнаружил, что амплитуда тока в цепи постоянно увеличивается. Основываясь на своих знаниях электродинамики, объясните наблюдения студента. Алгоритм решения

1 Определите, что вызывает увеличение амплитуды тока.

2 Объясните изменения, вызванные уменьшением индуктивности.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой индуктор питается переменным током:

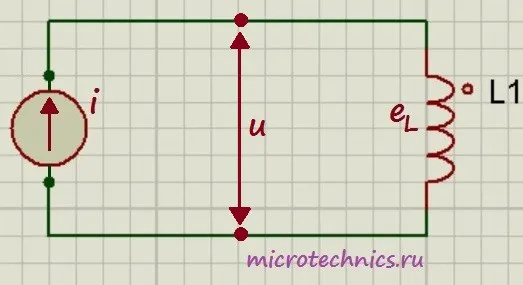
Давайте теперь рассмотрим временную зависимость тока и ЭДС индуктора, чтобы понять, почему они выглядят именно так:

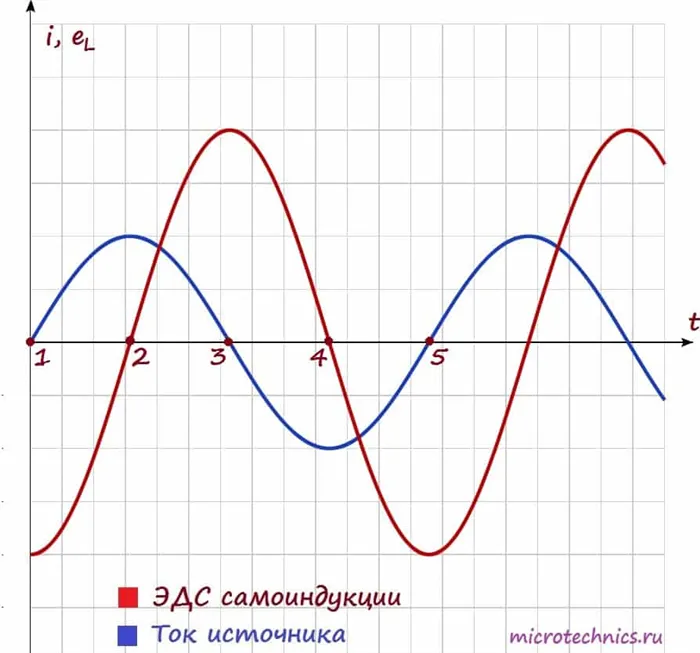
Как мы уже видели, HED нашего автопилота прямо пропорциональна и имеет противоположный знак скорости изменения тока:

\varepsilon_L = -L\medspace\frac

Диаграмма действительно иллюстрирует эту зависимость. Смотрите сами — между точками 1 и 2 ток изменяется, и чем ближе к точке 2, тем меньше изменение, а в точке 2 ток не меняет своего значения в течение короткого времени. Аналогично, скорость изменения тока максимальна в точке 1 и равномерно уменьшается по мере приближения к точке 2, а в точке 2 она равна 0, как видно на HED-диаграмме автоиндукции. Более того, в точке 1-2 ток увеличивается, и скорость его изменения положительна, поэтому ЭЭД в этой точке отрицательна.

Аналогично, ток уменьшается между точками 2 и 3 — скорость изменения тока отрицательна и увеличивается — ЭЭД индукции автопилота увеличивается и является положительной. Я не буду описывать другие части диаграммы — все процессы следуют одному и тому же принципу.

Кроме того, мы видим очень важный момент на графике — когда ток увеличивается (участки 1-2 и 3-4), ЭЭД самоиндукции и ток имеют разные знаки (участок 1-2: \варепсилон<0, i>0, участок 3-4: \varepsilon>0, i<0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены "навстречу" току источника).

Однако в случаях 2-3 и 4-5 происходит обратное — ток уменьшается, а ЭЭД препятствует уменьшению тока (поскольку индуктивный ток течет в том же направлении, что и ток источника, и частично компенсирует уменьшение тока).

Это подводит нас к очень интересному факту — индуктор имеет сопротивление переменному току, протекающему через цепь. Поэтому он имеет сопротивление, называемое индуктивным или реактивным, которое рассчитывается следующим образом:

X_L = w\medspace L

Где w — частота цепи: w = 2 \pi f. /latexf/latex — частота переменного тока. Поэтому чем выше частота тока, тем выше сопротивление катушки индуктора. А если ток постоянен (f = 0), то реактивность катушки равна 0, поэтому она не оказывает никакого влияния на протекающий ток.

Вернемся к диаграммам, которые мы рисовали для случая использования индуктора в цепи переменного тока. Мы определили самоиндукцию HED катушки, но каково напряжение u ? Здесь все просто, согласно 2-му закону Кирхгофа:

u + \varepsilon_L = 0

u = - \varepsilon_L

Нарисуем ток и напряжение в цепи как функцию времени на той же диаграмме:

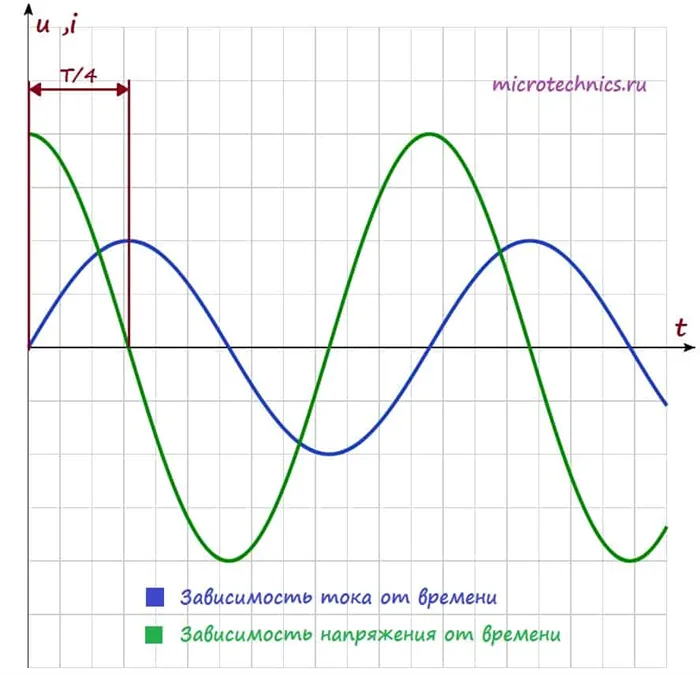
Как видите, ток и напряжение находятся вне фазы (соединены) друг с другом, и это одно из самых важных свойств цепей переменного тока с индукционной катушкой:

Энергия магнитного поля

Энергия магнитного поля показывает, какую работу совершил электрический ток в проводнике (индукционной катушке), чтобы создать это магнитное поле. Эта энергия, конечно, напрямую связана с индукцией проводника, вокруг которого создается магнитное поле.

Оказывается, что энергия магнитного поля равна половине произведения индуктивности контура и квадрата тока, т.е.

Если мы сравним эту формулу с формулой для кинетической энергии, то легко увидим, что они очень похожи

Эта формула гласит, что кинетическая энергия прямо пропорциональна массе движущегося объекта и квадрату его скорости.

Все это, конечно, не имеет прямого отношения к электротехнике. Однако мы уже несколько раз использовали механические аналогии при рассмотрении электромагнитных явлений, сравнивая энергию магнитного поля с кинетической энергией, эффект индукции с инерцией и, наконец, индукцию с механической массой. Сравнение этих формул также показывает, что ток в механике соответствует скорости движения.

ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждом из параллельно соединенных индукторов одинаково. Эквивалентная (общая) индуктивность параллельно соединенных индукторов может быть определена по следующей формуле:

Читайте также: Управление и защита приводов скольжения PCP1 без концевых выключателей.

Последовательное соединение индуктивностей

Ток, протекающий через последовательно соединенные катушки, одинаков, но напряжение на отдельных катушках разное. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек может быть рассчитана по следующей формуле:

Эти уравнения справедливы при условии, что магнитное поле отдельных катушек не влияет на соседние катушки.

Магнитные линии и магнитный поток

Магнитные силовые линии были экспериментально продемонстрированы вокруг магнита. Эти магнитные линии создают так называемое магнитное поле.

Как вы могли заметить на рисунке, концентрация магнитных силовых линий гораздо больше по краям магнита, чем в центре. Это означает, что магнитное поле сильнее всего на краях магнита, в то время как в центре магнита оно практически равно нулю. Направление магнитных силовых линий — с севера на юг.

Ошибочно думать, что магнитные силовые линии начинаются на северном полюсе и заканчиваются на южном. Это неправда. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть следующим образом.

Если сблизить два противоположных полюса, возникает магнитное притяжение.

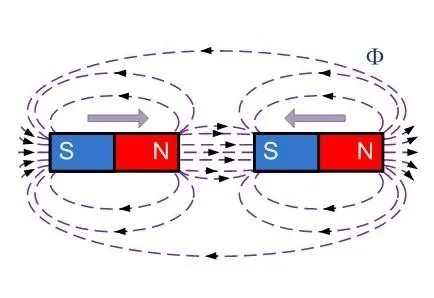
Если сблизить два полюса с одинаковым названием, они отталкиваются друг от друга.

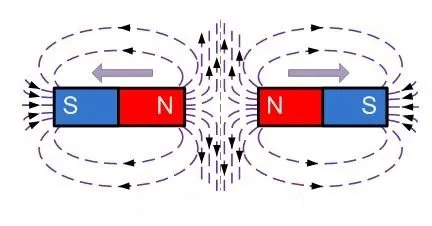
Ниже описаны наиболее важные свойства магнитных силовых линий.

Магнитные линии не поддаются гравитации.
Никогда не пересекаются между собой.
Всегда образуют замкнутые петли.
Имеют определенное направление с севера на юг.
Чем больше концентрация силовых линий, тем сильнее магнитное поле.
Слабая концентрация силовых линий указывает на слабое магнитное поле.

Магнитные силовые линии, образующие магнитное поле, также называются магнитным потоком.

Итак, давайте рассмотрим два рисунка и ответим на вопрос, где плотность магнитного потока будет больше. На рисунке «а» или на рисунке «б»?

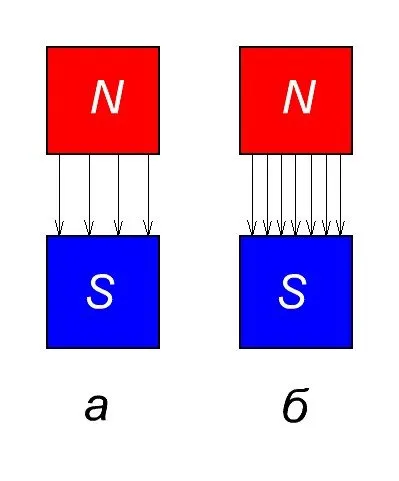
Мы видим, что на рисунке «a» есть только несколько магнитных линий, в то время как на рисунке «b» концентрация магнитных линий намного выше. Из этого можно сделать вывод, что плотность магнитного потока на рисунке b выше, чем на рисунке a.

В физике формула для магнитного потока записывается следующим образом

Ф — магнитный поток, Вебер

B — плотность магнитного потока, Тесла

a — угол между перпендикуляром n (обычно называемым нормалью) и плоскостью S, в градусах.

S — поверхность, через которую проходит магнитный поток, m 2

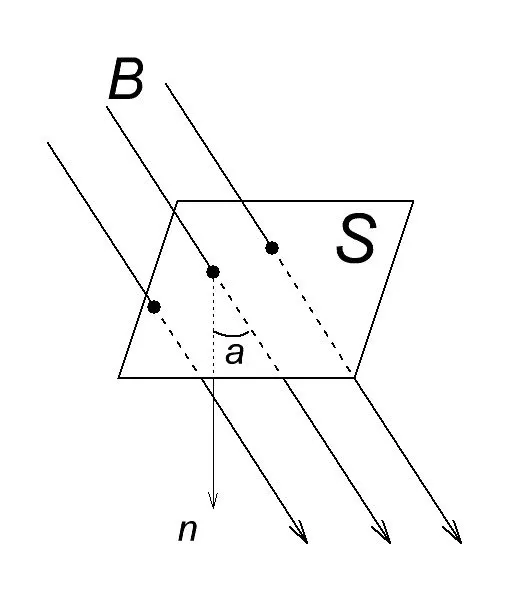
Что такое 1 Вебер? 1 Вебер — это магнитный поток, создаваемый полем индукции в 1 Тесла через площадь в 1 м 2, перпендикулярную направлению магнитного поля.

Характеристика колебаний

Фаза определяет состояние системы, т.е. координаты, скорость, ускорение, энергию и т.д.

Циклическая частота описывает скорость, с которой меняется фаза колебания.

Начальное состояние колебательной системы характеризуется начальной фазой

Амплитуда A — это наибольшее отклонение от положения равновесия.

Период T — это интервал времени, за который точка совершает полное колебание.

Частота колебаний — это количество полных колебаний за единицу времени t.

Частота, цикловая частота и период связаны друг с другом следующим образом

Читайте также: Основные параметры центробежного насоса

Векторная диаграмма электрической цепи

Чтобы вывести закон Ома для цепи переменного тока, показанной на рисунке 2.20, нам нужно уметь складывать мгновенные напряжения напряжений, находящихся вне фазы друг с другом. Самый простой способ выполнить сложение нескольких гармоник — использовать векторные диаграммы, рассмотренные в разделе 1.11. С помощью векторной диаграммы электрических колебаний в цепи можно определить амплитуду тока как функцию амплитуды напряжения и сдвига фаз между током и напряжением.

Поскольку ток одинаков во всех частях цепи, удобно начать построение векторной диаграммы с вектора тока m. Этот вектор представлен в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с током. Поэтому вектор mR должен иметь то же направление, что и вектор m. Его величина UmR = ImR.

Колебания напряжения в индукционной катушке опережают колебания тока на π/2, и соответствующий вектор mL должен быть повернут на π/2 относительно вектора m. Его величина UmL = ImωL. Если предположить, что положительный сдвиг фазы соответствует вращению вектора против часовой стрелки, то вектор mL должен повернуться на π/2 влево (можно, конечно, сделать и наоборот).

Вектор напряжения на конденсаторе mC лежит на π/2 позади вектора m и поэтому поворачивается на этот угол вправо по отношению к вектору m. Его мера равна

Чтобы найти вектор полного напряжения m, сложите три вектора: mR, mL и mC. Удобнее сначала сложить два вектора mL и mC (рисунок 2.22). Мера этой суммы равна, если Именно такой случай показан на рисунке. Если сложить вектор mL + mC с вектором mR, то получится вектор m, который характеризует колебания напряжения в сети.

По теореме Пифагора (из треугольника AOB):

Из уравнения (2.9.2) можно определить амплитуду тока в цепи:

Это закон Ома для цепи переменного тока, показанной на рисунке 2.20.

Из-за сдвига фаз между напряжениями в разных частях цепи полное сопротивление Z цепи (см. рис. 2.20) выражается следующим образом:

По амплитудам тока и напряжения можно судить о реальных значениях этих величин. Они имеют такое же отношение друг к другу, как и амплитуды в (2.9.3):

Мгновенное значение тока изменяется гармонически со временем:

i = Im sin (ωt + φc), (2.9.6)

где φc — разность фаз между силой тока и напряжением сети. Она зависит от частоты c и параметров цепи R, L, C.

Колебания и их амплитуда

Повторяющиеся движения или процессы называются осцилляциями.

В зависимости от типа колебаний, они могут быть механическими, электромагнитными, акустическими и т.д. колебания. Различные типы колебаний описываются одними и теми же уравнениями и одинаковыми свойствами.

Вибрация называется свободной вибрацией

(Колебания, обусловленные энергией, которую вибрирующая система однажды получила, после чего на эту систему больше не оказывается внешнего воздействия.

Читайте также: Заточка кухонного ножа с помощью точильного камня

Самый простой тип колебаний — гармоническое колебание.

Гармонические колебания — это самый простой тип колебаний.

Это колебания, при которых колеблющаяся величина изменяется во времени в соответствии с законами синуса и косинуса.

Если предположить, что существуют гармонические колебания параметра $s$, то эти колебания могут быть описаны следующим уравнением:

Где $A=s_$ — амплитуда колебаний,
[H1toH2]

Характеристика колебаний

Фаза определяет состояние системы, т.е. координаты, скорость, ускорение, энергию и т.д.

Циклическая частота описывает скорость, с которой меняется фаза колебания.

Начальное состояние колебательной системы характеризуется начальной фазой

Амплитуда A — это наибольшее отклонение от положения равновесия.

Период T — это интервал времени, за который точка совершает полное колебание.

Частота колебаний — это количество полных колебаний за единицу времени t.

Частота, цикловая частота и период связаны друг с другом следующим образом

Читайте также: Основные параметры центробежного насоса

Векторная диаграмма электрической цепи

По теореме Пифагора (из треугольника AOB):

Из уравнения (2.9.2) можно определить амплитуду тока в цепи:

Это закон Ома для цепи переменного тока, показанной на рисунке 2.20.

Мгновенное значение тока изменяется гармонически со временем:

i = Im sin (ωt + φc), (2.9.6)

где φc — разность фаз между силой тока и напряжением сети. Она зависит от частоты c и параметров цепи R, L, C.

0$ — циклическая (циклическая) частота колебания; $varphi$ — начальная фаза колебания (фаза при $t=0$); $(_0t+varphi )$ — фаза колебания.

Амплитуда — это максимальное значение величины, для которой рассматривается колебание. Поскольку косинус (как и синус) изменяется в пределах от единицы до минус единицы, значение $s$ находится в диапазоне $-Ale sle 3500A.

[/H1toH2]

Катушка индуктивности в цепи переменного тока – принцип действия и значение

Сегодня мы рассмотрим индукционную катушку в цепи переменного тока и узнаем, какая разница была бы, если бы цепь работала на постоянном токе, а также много интересных особенностей этого простого, но очень важного радиокомпонента.

Теоретика
- Что такое катушка индуктивности
- Конструкционные особенности
- Применение
- Основные характеристики катушек индуктивности
- Цепь, питаемая постоянным током
- Включение в цепь с переменным током
Теоретика

Давайте сначала определим цель этой части и основные понятия и термины в данном контексте.

Что такое катушка индуктивности

Индукционная катушка — это радиоэлемент, используемый в различных схемах для следующих целей:
- Сглаживание биений;
- Подавление помех;
- Ограничение переменного тока;
- Накопление энергии и прочее.
Это спиральная, винтовая или намотанная катушка изолированного проводника. Деталь имеет относительно низкую емкость и сопротивление, но также высокую индуктивность, что означает, что в проводнике может возникать электромагнитная сила при протекании тока в цепи.
- Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
- Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.
- Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.
Интересно знать! Магнитное поле внутри соленоида однородно. Это магнитное поле может совершать механическую работу, притягивая ферритовый сердечник.
- Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
- Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.
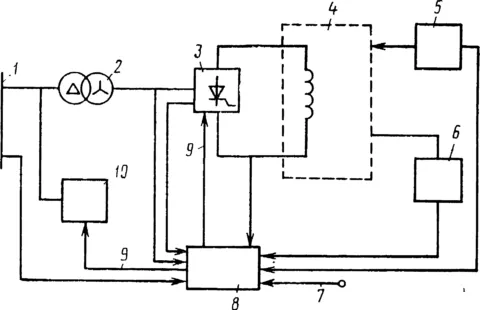
- Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.
Конструкционные особенности

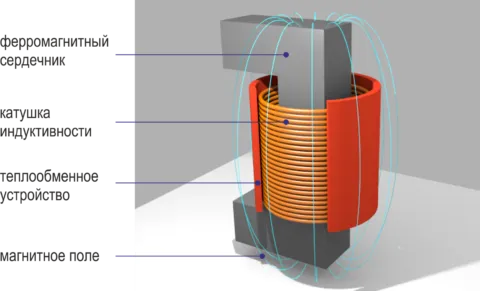
Конструктивно индукционная катушка состоит из намотанного или накрученного изолированного одножильного или многожильного проводника (обычно это окрашенный медный провод) вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной или квадратной. Материалы, используемые для сердечника, имеют более высокую магнитную проницаемость, чем воздух, что позволяет удерживать магнитное поле вблизи катушки и увеличивает индуктивность.

Включение катушки индуктивности в цепи с постоянным и переменным током

В общем, мы определили, что такое индукционная катушка, для чего она используется и какие свойства важны для расчета ее параметров, но неопытному читателю пока не ясно, как изменяются параметры тока, протекающего через этот участок.

Цепь, питаемая постоянным током

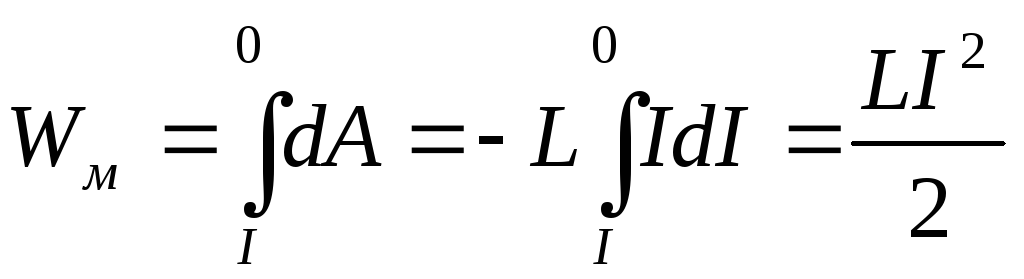
Чтобы упростить описание, мы проведем очень простой эксперимент:
- Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.
- Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.
- Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
- Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.
- При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.
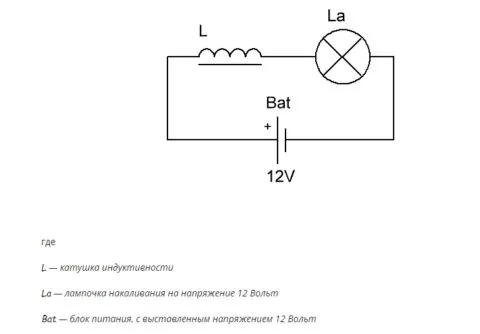
- Теперь берем все наши детали и соединяем их по приведенной выше схеме.
- Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.
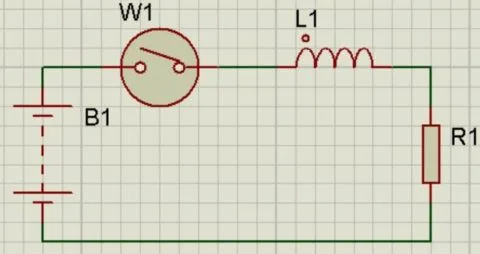
В этой схеме лампа заменена резистором, но это не важно.
- Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
- Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
- Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
- Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.