W = n Δ ν = 1 АТМ × 2 м3 × 101325 Па = 202, 650 Дж
времена 2 времена 101325 = 202 650 >что, конечно, идентично разнице между Δ CHAS и Δ U .
Уравнение состояния газа
При изучении термодинамических процессов воздух рассматривается как идеальный газ, т.е. газ, в котором молекулы имеют бесконечный объем, но конечную массу, и между молекулами нет сил взаимодействия.
Состояние воздуха (и любого другого идеального газа) может быть описано уравнением Менделеева-Клапейрона:
Это уравнение связывает основные физические величины, характеризующие состояние газа:
- р — давление
- V — объем
- Т — температура
- m — масса
Газовая постоянная R равна работе расширения, совершаемой 1 кг газа при нагревании на 1 К при постоянном давлении.
При сжатии и расширении газа его свойства меняются. На основе определяющего уравнения зависимость состояния газа можно экстраполировать на различные процессы, характеризующиеся различными условиями течения. Давайте теперь рассмотрим каждый из возможных характерных процессов в отдельности.
Изотермический процесс
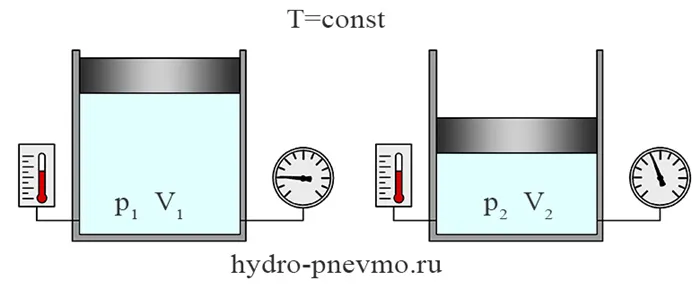
Изотермический процесс — это термодинамический процесс, протекающий при постоянной температуре. При T1= Т2Согласно закону Бойля-Мариотта, pV=const, т.е. в изотермическом процессе давление газа обратно пропорционально его объему.
Адиабатический процесс
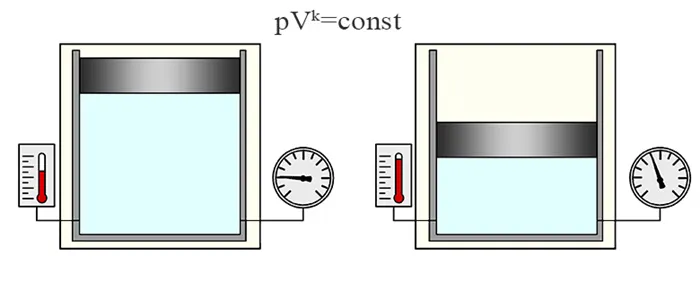
Адиабатический или адиабатический процесс — это процесс, в котором отсутствует теплообмен с окружающей средой. К этому процессу применима формула Пуассона:
Где k — адиабатический коэффициент k = cp/cv(для воздуха k = 1,4). Зависимости между физическими величинами, характеризующими состояние газа в адиабатическом процессе, следующие:
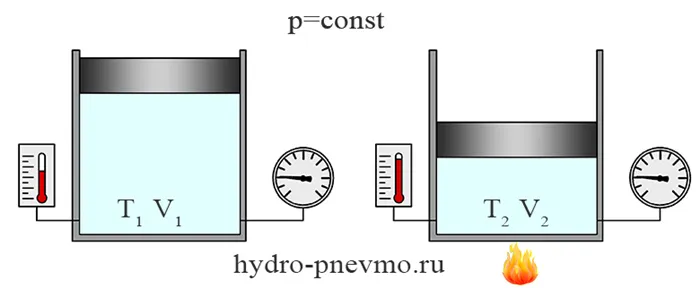
Изотермический процесс
Считается, что идеальный газ претерпевает изотермический процесс при температуре. В ходе процесса изменяются только давление газа и его объем.
Рассмотрим любые два состояния газа: В одном из двух состояний значения макроскопических параметров равны, а во втором -. Эти величины связаны уравнением Менделеева-Клапейрона:
Как уже упоминалось в начале, масса и молекулярная масса предполагаются постоянными.
Поэтому правые части данных уравнений равны. Следовательно, левые стороны также равны:
Поскольку два состояния газа были выбраны произвольно, можно сделать вывод, что в изотермическом процессе произведение давления газа на его объем остается постоянным:
Это утверждение известно как закон Бойля-Мариотта.
Закон Бойля-Мариотта называется законом Бойля-Мариотта.
В изотермическом процессе давление газа обратно пропорционально его объему. Например, при изотермическом расширении газа, если его объем увеличивается в три раза, давление газа также уменьшается в три раза.
Как можно физически объяснить обратную зависимость давления от объема? При постоянной температуре средняя кинетическая энергия молекул газа остается неизменной, то есть сила, с которой молекулы ударяются о стенки сосуда, не меняется — проще говоря. По мере увеличения объема концентрация молекул уменьшается, а следовательно, уменьшается число столкновений молекул в единицу времени на единицу площади стенки — давление газа падает. И наоборот, при уменьшении объема концентрация молекул увеличивается, их столкновения становятся более частыми, и давление газа возрастает.
Графики изотермического процесса
Как правило, диаграммы термодинамических процессов изображаются в следующих системах координат:
-Диаграмма: ось абсцисс, ось ординат; -Диаграмма: ось абсцисс, ось ординат; -Диаграмма: ось абсцисс, ось ординат.
График изотермического процесса называется изотермическим.
Изотерма н а-диаграмме — это график обратной зависимости.
Такой график — это гипербола (в алгебре — график функции). Изотермическая гипербола показана на рисунке 1.
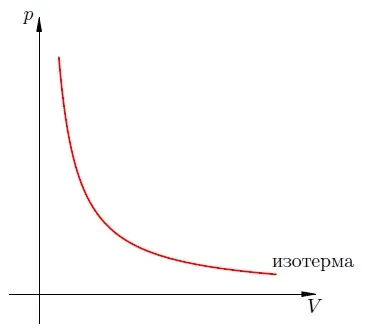
Рисунок 1: Изотерма н а-графике.
Каждая изотерма соответствует определенному значению постоянной температуры. Видно, что чем выше температура, тем выше соответствующая изотерма н а-графике.
Рассмотрим два изотермических процесса, происходящих с одним и тем же газом (рис. 2). Первый процесс происходит при температуре, второй — при температуре.
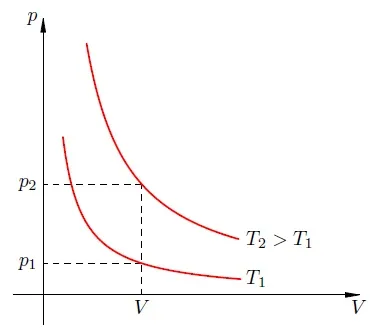
Рисунок 2: Чем выше температура, тем выше изотерма.
Фиксируем некоторое значение объёма. На первой изотерме ему отвечает давление, на второй — p_1′ alt=’p_2>p_1′ />. Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, T_1′ alt=’T_2>T_1′ />.
В двух других системах координат изотерма выглядит очень просто: Это прямая линия, перпендикулярная оси (рис. 3):
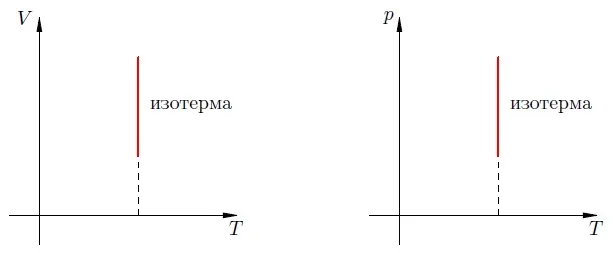
Рисунок 3. Изотермы в и-диаграммы.
Изобарный процесс
Опять же, изобарический процесс — это процесс, который происходит при постоянном давлении. Изобарический процесс изменяет только объем газа и его температуру.
Типичным примером изобарического процесса является газ под огромным поршнем, который свободно движется. Если масса поршня и площадь поперечного сечения поршня, то давление газа постоянно и равно
где имеется в виду атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении. Рассмотрим снова любые два состояния газа; на этот раз значения макроскопических параметров равны и .
Запишем определяющие уравнения:
Разделив их друг на друга, получим :
В принципе, этого должно быть достаточно, но давайте пойдем немного дальше. Мы переписываем это уравнение так, чтобы одна часть содержала только параметры первого состояния, а другая — только параметры второго состояния (другими словами, мы разделяем индексы на разные части):
И с этого момента — учитывая произвольность выбора государств! — получаем закон Гей-Люссака:
Другими словами: Если давление газа постоянно, то его объем прямо пропорционален температуре:
Почему объем увеличивается с ростом температуры? При повышении температуры молекулы ударяются сильнее и поднимают поршень. В то же время концентрация молекул уменьшается, а удар становится меньше, так что давление в итоге сохраняет прежнее значение.
Математические формулы
Состояние газовых масс характеризуется температурой, объемом и давлением. Уравнение используется для установления взаимосвязи между показателями. Формула используется в физических задачах для изучения внутреннего теплового процесса. Наиболее важные параметры уравнения молекулярно-кинетической теории газов:
- р — давление, измеряется в паскалях, обозначается Па;
- m — масса (кг);
- n — концентрация молекул на определённом участке.
На уроках физики и на практике для анализа состояния газа используются различные выражения. Уравнение Клайперона-Менделеева используется в курсах физики и в полевых условиях для описания состояния газа. Экспоненты, составляющие это уравнение, равны.
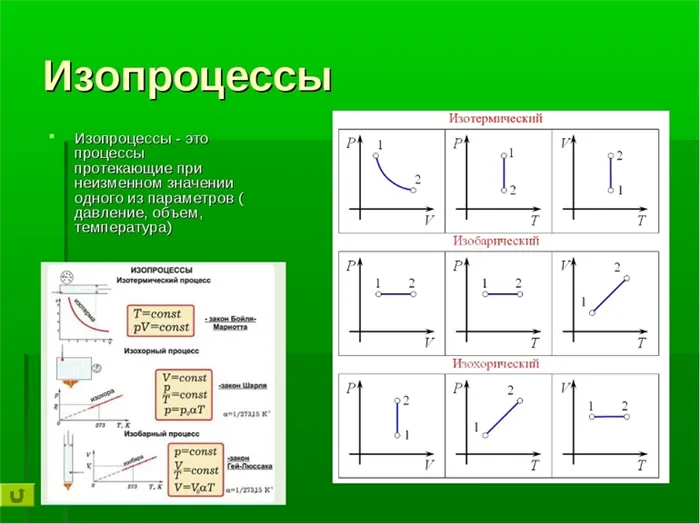
- р — давление;
- V — объём;
- Т — температура;
- m — масса;
- М — молярная масса, которая измеряется в кг/моль;
- R — считается универсальной постоянной, где k — постоянная Больцмана, а Na — постоянная Авогадро.
Значения последних двух индексов приведены в специальных таблицах молекулярной физики. Когда в задаче описывается переход газов из одного состояния в другое, используется уравнение Клайперона. Для данной массы газа произведение VP, деленное на абсолютную температуру, является константой. Параметры в моменты времени 1 и 2 рассчитываются отдельно.
Дополнительные выражения используются для расчета энергии, энтропии (беспорядка) и порядка, концентрации и других параметров в молекулярно-кинетической теории (MKT):
- Сокращенная формула состояния газа в идеальном виде. Для записи применяется постоянная Больцмана (k), концентрация молекул (n), температура газа (t).
- Формула плотности веществ. Её можно получить из главного уравнения.
- Закон Дальтона: давление газов из смеси равно сумме парциальных давлений всех газовых компонентов.
- Парциальное P. Используется для расписания состояния всех компонентов смеси и определения давления одного вещества, если бы оно занимало сосуд на 100%.
Дополнительные процессы

Эксперименты с адиабатическими или адиабатическими (изоэнтропическими) процессами, связанные с термодинамикой, проводятся в практических курсах физики. При этом явлении теплообмен с внешней средой отсутствует. Для наблюдения общего случая всех описанных выше процессов используется газ с постоянной теплоемкостью. Это явление называется мультимодальным.
При одинаковом давлении и температуре компонентов и одинаковом объеме используемые идеальные газы содержат одинаковое число молекул. На одну молекулу различных веществ приходится N A = 6,02-10 23 молекул. Это число называется числом Авогадро.
Согласно закону Дальтона, давление смеси равно сумме парциальных давлений составляющих ее компонентов. Выражение записывается следующим образом: P см=P1+P2+…Pn. Последнее число Pn — это давление газа, который занимал бы весь объем контейнера.
В школьной физике изохорные процессы чаще всего описываются как переход идеального газа из одного состояния в другое без изменения его объема. Впервые это явление было изучено французом Жаком Шарлем. Закон заключается в следующем. Поскольку v=const и V=const, следующее уравнение справедливо для всех различных состояний веществ. Математически закон Шарля описывается следующим образом: P/T/T=const.
Это выражение показывает, что между температурой и давлением существует прямо пропорциональная зависимость. Если P увеличивается, то T также увеличивается, и наоборот. Графическое изображение зависимости между этими величинами называется изохорой. В интервале абсолютного нуля для кривых предусмотрена условная зависимость. Прямая линия приведена к началу координат пунктирными линиями.
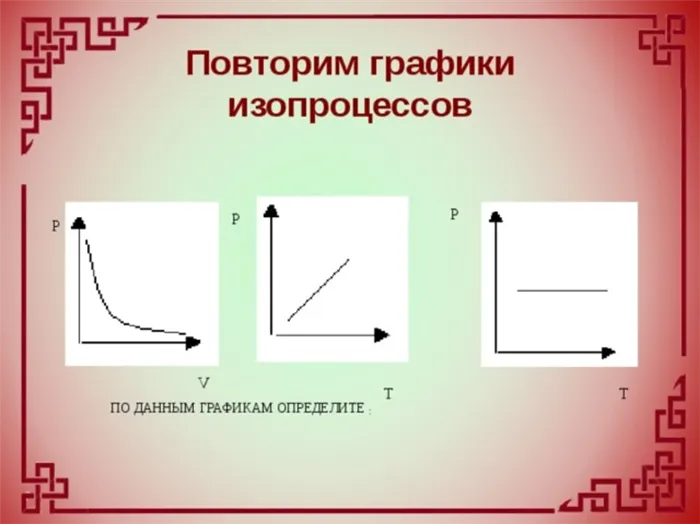
Эта зависимость T от P и V в изобарных и изохорных процессах определяет точность и эффективность измерения температуры с помощью газовых термометров. Ученые первыми обнаружили эти явления, которые являются частными случаями конститутивного уравнения. Позже физики подтвердили закон Клапейрона и Менделеева.
В хронологическом порядке сначала изучались процессы, развивающиеся при постоянной температуре и в одном объеме. Изобарические процессы рассматривались в последнюю очередь. Редким и интересным явлением является изоэнтропия, когда термодинамическая система изменяется при условии постоянной энтропии. Последнее записывается как S=const.
В качестве примера рассматривается адиабатический обратимый процесс. Для расчета идеального газа используется следующее уравнение: pV γ = const, где γ — показатель адиабаты (определяется типом газа). Адиабатический эффект характеризуется отсутствием теплопоступлений и потерь. Физики считают такие процессы быстротекущими.








