После вопросов читателей моей публикации 1 об условиях возбуждения автоаталлации в механической системе, я решил подробно описать явление возникновения и поддержания автоаталлации и выделить основные области ее возникновения и применения.
Механизм возникновения автоколебаний
| Раздел представляет собой | Физическая и механическая энергия. |
| См. | Статья |
| Язык | Русский |
| Дата добавления | 25.12.2013 |
| Размер | 90,7 K |
Студенты, аспиранты и молодые ученые, которые используют базу знаний для своей учебы и работы, будут очень благодарны.
Доступно на сайте http://www.allbest.ru
Автоколебания — это незатухающие колебания в диффузионной динамической системе с нелинейной обратной связью, поддерживаемой энергией постоянного, т.е. непериодического, внешнего воздействия. Самоколебания отличаются от вынужденных колебаний тем, что последние вызываются периодическим внешним воздействием и возникают с частотой этого воздействия, тогда как возникновение самоколебаний и их частота определяются внутренними свойствами самоколеблющейся системы.
Термин автоколебания был введен в русскую терминологию А.А. Андроновым в 1928 году.
Удар молотком с использованием энергии цепи переменного тока, частота которого во много раз ниже частоты тока в цепи.
Катушка L колебательного контура размещается над столом (или другим объектом, по которому нужно нанести удар). Железная труба, нижний конец которой образует ударную часть молота, вставляется снизу. Трубка снабжена вертикальной щелью для уменьшения токов Фуко. Параметры колебательного контура выбираются таким образом, чтобы его собственная частота совпадала с частотой тока в цепи (например, городской переменный ток, 50 Гц).
После включения тока и возникновения колебаний наблюдается резонанс токов в цепи и во внешней цепи, и железная трубка втягивается в катушку. Индуктивность катушки увеличивается, колебательный контур выходит из резонанса, и амплитуда колебательного тока в катушке уменьшается. Поэтому трубка возвращается в исходное положение — вне катушки — под действием силы тяжести. Затем колебания тока в контуре усиливаются, и снова возникает резонанс: трубка втягивается обратно в катушку.
Затем трубка периодически вибрирует вверх-вниз, ударяя по столу, как молотком. Период этих механических автоколебаний в десять раз больше, чем поддерживающий их переменный ток.
Молоток назван в честь М.И. Маклакова, ассистента Московского физико-технического института, который предложил и провел этот эксперимент для доказательства автоколебаний.
Рисунок 1: Механизм автоколебаний.
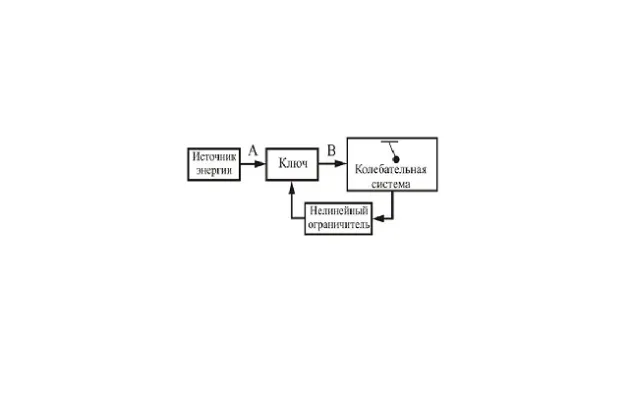
Автоматические колебания могут быть различной природы: механические, тепловые, электромагнитные, химические. Механизм генерации и поддержания автоколебаний в различных системах может быть основан на различных физических или химических законах. Для точной количественной оценки автоколебаний различных систем могут потребоваться различные математические методы. Однако можно представить общую для всех автоколебательных систем схему, которая качественно описывает этот механизм (рис. 2).
Рисунок 2: S — источник постоянного (непериодического) воздействия; R — нелинейный контроллер, преобразующий постоянное воздействие в изменяющееся (например, временно прерывистое) воздействие, которое заставляет осциллятор «колебаться» V — колеблющийся элемент (или элементы) системы. А колебания осциллятора управляют работой контроллера R через обратную связь B, регулируя фазу и частоту его действия.
Автоматический качающийся маятник Маклакова
Подобные документы
Понятие автоколебаний как незатухающих колебаний, возникающих в замкнутой системе с обратной связью и внешним постоянным источником энергии. Примеры автоколебаний в физических процессах. Механические примеры автоколебаний.
Свободное колебание осциллятора при отсутствии сопротивления. Природа вынужденных колебаний, их возникновение. Схема для исследования свободных колебаний в линейной системе. Фазовая диаграмма колебательной системы с усилением источника.
Определение понятия осцилляторных процессов. Математическое представление и графическая иллюстрация незатухающих и затухающих колебаний в электрической цепи. Исследование вынужденных колебаний в электрической цепи под действием периодической электродвижущей силы.
Разработка электронных устройств. Общая информация о микропроцессорной системе. Принцип работы тактового генератора на микроконтроллере Atmega 8. Его архитектура и программирование. Понятие и расчет надежности системы. Улучшение количества периферийных устройств.
Изучение динамики затухающего колебательного движения на примере крутильного маятника, определение основных свойств диффузионной системы. Крутильный маятник как диффузионная система. Расчет периода колебаний маятника без кольца и с кольцом.
Первая теорема Гельмгольца. Уравнение равновесия для внутренней энергии и силы ее распада. Обобщенное уравнение Гельмгольца для дисперсии вихря в вязкой несжимаемой среде. Квазитвердое движение внутри вихря Ранкина и индуцированное поле вне вихря.
Назначение и технические характеристики устройства. Краткое описание работы устройства. Требования к системе управления электроприводом. Выбор модулей и устройств системы управления. Краткий принцип работы.

- главная
- рубрики
- по алфавиту
- вернуться в начало страницы
- вернуться к началу текста
- вернуться к подобным работам
Примерами автоколебаний являются:
- незатухающие колебания маятника часов за счёт постоянного действия тяжести заводной гири;
- колебания скрипичной струны под воздействием равномерно движущегося смычка
- возникновение переменного тока в цепях мультивибратора и в других электронных генераторах при постоянном напряжении питания;
- колебание воздушного столба в трубе орга́на, при равномерной подаче воздуха в неё. (см. также Стоячая волна)
- вращательные колебания латунной часовой шестерёнки со стальной осью, подвешенной к магниту и закрученной (опыт Гамазкова) (кинетическая энергия колеса, как в униполярном генераторе преобразуется в потенциальную энергию электрического поля, потенциальная энергия электрического поля, как в униполярном двигателе, преобразуется в кинетическую энергию колеса и т.д. )
Молоток Маклакова
Удар молотком с энергией цепи переменного тока, частота которого во много раз ниже частоты цепи 2.

Катушка L колебательного контура размещается над столом (или другим объектом, по которому нужно нанести удар). Железная труба, нижний конец которой образует ударную часть молота, вставляется снизу. Трубка снабжена вертикальной щелью для уменьшения токов Фуко. Параметры колебательного контура выбираются таким образом, чтобы его собственная частота совпадала с частотой тока в цепи (например, городской переменный ток, 50 Гц).
После включения тока и возникновения колебаний наблюдается резонанс токов в цепи и во внешней цепи, и железная трубка втягивается в катушку. Индуктивность катушки увеличивается, колебательный контур выходит из резонанса, и амплитуда колебательного тока в катушке уменьшается. Поэтому трубка возвращается в исходное положение — вне катушки — под действием силы тяжести. Затем колебания тока в контуре усиливаются, и снова возникает резонанс: трубка втягивается обратно в катушку.
Трубка вибрирует вверх-вниз и ударяется о стол с громким, похожим на молоток, звоном. Период этих механических автоколебаний в десять раз длиннее, чем переменный ток, который приводит их в движение.
Молоток назван в честь М.И. Маклакова, ассистента Московского физико-технического института, который предложил и осуществил этот эксперимент по обнаружению автоколебаний.
Механизм автоколебаний

Существуют различные типы автоколебаний: механические, тепловые, электромагнитные и химические. Механизм возникновения и поддержания автоколебаний в различных системах может быть основан на различных физических или химических законах. Для точной количественной оценки автоколебаний различных систем могут потребоваться различные математические методы. Однако можно представить общую для всех автоколебательных систем схему, которая качественно описывает этот механизм (рис. 1). На схеме: S — источник постоянного (непериодического) воздействия; R — нелинейный регулятор, преобразующий постоянное воздействие в изменяющееся (например, прерывистое во времени) воздействие, которое «колеблет» колеблющийся элемент (элементы) системы V, а колебания управляют работой регулятора R через обратную связь B, определяя фазу и частоту его действия. Дисперсия (диссипация энергии) в автоколебательной системе восстанавливается за счет поступления энергии от непрерывного источника удара, поэтому автоколебания не затухают.
Если колеблющийся элемент системы способен к собственным затухающим колебаниям (так называемый гармонический диссипативный осциллятор), то автоколебания (при равенстве диссипации и вводимой в систему энергии за период) устанавливаются на частоте, близкой к резонансной для этого осциллятора, их форма становится близкой к гармонической, а амплитуда в определенном диапазоне значений становится тем больше, чем больше величина постоянного внешнего воздействия. Примером такой системы является храповой механизм маятниковых часов, форма которого показана на рисунке 2. На ось храпового колеса A (которое в данной системе принимает на себя функцию нелинейного регулятора) действует сила постоянного крутящего момента M, которая передается через зубчатое колесо с помощью навитой пружины или груза. Когда колесо A вращается, его зубцы подают мгновенные импульсы на маятник P (осциллятор), которые заставляют его колебаться. Кинематика механизма играет роль обратной связи в системе, синхронизируя вращение колеса с колебаниями маятника таким образом, что колесо поворачивается на угол, соответствующий одному зубу за полный период колебаний.
Самоколеблющиеся системы, не содержащие осцилляторов, называются релаксационными. Колебания могут сильно отличаться от гармоник и могут быть прямоугольными, треугольными или трапециевидными. Амплитуда и период релаксационных собственных колебаний определяются соотношением между величиной установившегося действия и инерционными и диффузионными свойствами системы.
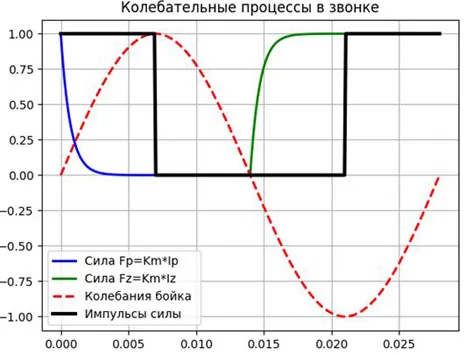
Простейшим примером релаксационных колебаний является работа электрического звонка, показанного на рис. 3… Источником постоянного (непериодического) воздействия является электрическая батарея U; роль нелинейного регулятора играет выключатель T, который замыкает и размыкает цепь, вызывая появление в ней прерывистого тока; колебательными элементами являются магнитное поле, периодически индуцируемое в сердечнике электромагнита E, и якорь A, который движется под действием переменного магнитного поля. Колебания якоря активируют переключатель, который образует цепь обратной связи. Инерция этой системы определяется двумя различными физическими величинами — инерцией якоря A и индуктивностью обмотки магнита E. Увеличение одной из этих двух величин приводит к увеличению периода колебаний.
В природе и технике
Автоколебания лежат в основе многих физических явлений:
- колебания листьев растений под действием равномерного потока воздуха;
- образование турбулентных потоков на перекатах и порогах рек;
- голоса людей, животных и птиц образуются благодаря автоколебаниям, возникающим при прохождении воздуха через голосовые связки;
- действие регулярных гейзеров
- Система «атмосфера — лёд — океан»
Большое количество технических устройств и аппаратов основано на автоколебаниях, в том числе следующие:
- работа всевозможных часов, как механических, так и электрических;
- звучание всех духовых и струнно-смычковых музыкальных инструментов;
- действие всевозможных генераторов электрических и электромагнитных колебаний, применяемых в электротехнике, радиотехнике и электронике;
- работа поршневых паровых машин и двигателей внутреннего сгорания;
- некоторые системы автоматического регулирования работают в режиме автоколебаний, когда регулируемая величина колеблется в окрестности требуемого значения, то превышая его, то опускаясь ниже него, в допустимом для целей регулирования диапазоне (например, система терморегулирования бытового холодильника).


Обрушение моста Теком (США, Вашингтон, округ Колумбия) 7 ноября 1940 года, вызванное самоколебаниями, вызванными ветром.
В то же время, автоколебания могут возникать в некоторых технических системах, не предусмотренных разработчиками этих систем, в результате недосмотра при выборе технических параметров. Такие естественные колебания могут быть нежелательными (например, «скрежет» крана при определенных скоростях потока воды) и часто являются катастрофическими, вызывая аварии с серьезными последствиями при работе с системами, в которых циркулирует большое количество энергии. Например:
- в турбинах электростанций;
- в реактивных авиационных (помпаж) и ракетных двигателях;
- в магистралях газов и жидкостей высокого давления;
- флаттер различных элементов летательных аппаратов;
- автоколебания сооружений неустойчивой аэродинамической формы при обтекании их потоком воздуха с определённой скоростью (явление ветрового резонанса) и др.
Автоколебательные системы
В любой реальной системе существуют потери энергии. Реальные колебания в реальных условиях не могут происходить без затрат энергии. Поэтому в реальности немодулированные колебания всегда являются вынужденными. Они постоянно получают энергию, чтобы компенсировать потери.

Однако процесс восполнения энергии может происходить по-разному. Поршень насоса, например, колеблется под действием сил, оказываемых на него механизмом на приводном валу. Здесь поршень колеблется с частотой, определяемой извне, и вся подводимая энергия немедленно используется для приведения в движение перекачиваемой жидкости.
Другой вариант восполнения энергии — маятник часов. При каждом колебании маятник пополняет запас энергии анкерного механизма. Существенное отличие заключается в том, что частота пополнения энергии маятника регулируется самим маятником.
Если в насосе параметры не имеют значения — колебания будут продолжаться с частотой, задаваемой валом, то в маятнике ситуация иная. Увеличение жесткости пружины или массы баланса изменит частоту колебаний, так как качающийся маятник изменяет частоту поступления энергии от анкерного механизма.
Системы, в которых затухающие колебания происходят из-за подвода энергии к управляемой системе, называются самоколеблющимися. Колебания, возникающие в таких системах, называются автоколебаниями. В отличие от вынужденных колебаний, автоколебания существуют в системе без внешних воздействий.
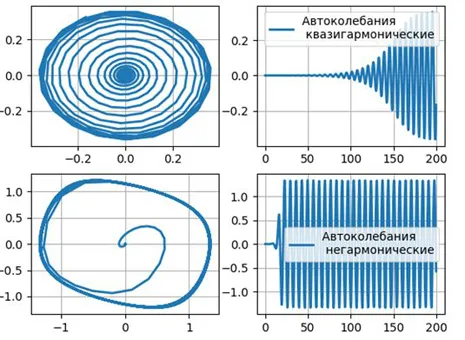
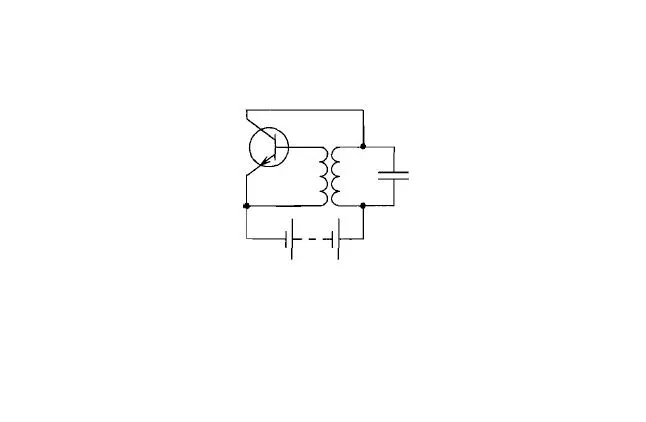
Другим примером колебательной системы является электрический генератор с контуром, состоящим из конденсатора и катушки. Свободные колебания могут присутствовать в цепи в затухающей форме. Чтобы сделать колебания в цепи самоосциллирующими, необходимо добавить в систему специальный элемент, компенсирующий потери энергии в цепи, с периодом собственных колебаний цепи (найденным по формуле Томсона $T=2\pi \sqrt$).
Таким элементом обычно является транзистор. Часть напряжения в индукторе прикладывается к управляющему электроду (базе) транзистора, и энергия поступает в цепь через секцию коллектор-эмиттер транзистора.
Элементы автоколебательной системы
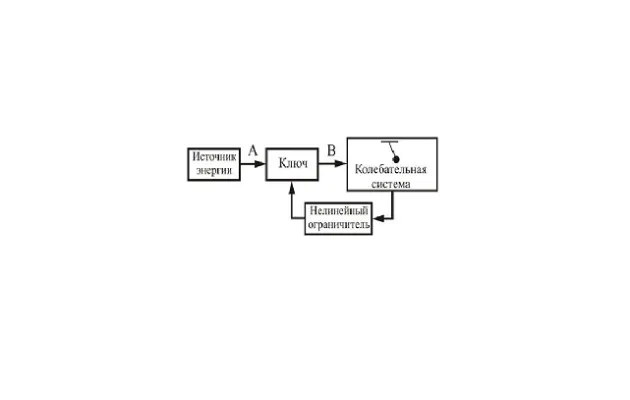
Выделим элементы автоматической осциллирующей системы:
- источник, за счет которого восполняются потери энергии колебаний;
- элемент, в котором возможно существование свободных затухающих колебаний;
- устройство, регулирующее поступление энергии от источника;
- обратная связь, управляющая регулирующим устройством, в зависимости от фазы колебаний.
Каждая автоколебательная система имеет эти элементы. Отсутствие любого из этих элементов приводит к тому, что колебания затухают или вообще невозможны.
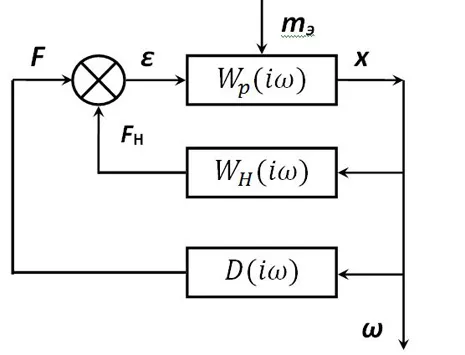
Мы начинаем серию статей, посвященных автоколебаниям с точки зрения теории управления. Статьи рассчитаны на образованного читателя и очень насыщены теорией, хотя и не обосновывают все утверждения в деталях.
Автоколебания — это периодические процессы в нелинейных системах, которые часто возникают в системах. В практике автоматического управления важное значение имеет авторегрессионное поведение систем. В нелинейных системах, в отличие от линеаризованных моделей, не происходит неограниченного увеличения переменной состояния при потере устойчивости и отклонения колебательного характера неустойчивости на амплитуду, определяемую параметрами системы. Кроме того, автоколебательные режимы часто используются для контроля различных физических параметров технологических процессов, например, температуры. При этом учитываются ограничения на допустимые частоты и амплитуды колебаний.
Точная форма и параметры периодических режимов могут быть определены только для определенных типов систем, например, релейных систем. Наиболее удобным методом изучения предельных циклов в системах второго (а иногда и третьего) порядка является метод фазовой плоскости. Однако такой подход практически невозможен для большинства систем, описываемых моделями высокого порядка со сложной нелинейностью.
Одним из способов получения информации о существовании и параметрах автоколебательных режимов является метод гармонического равновесия.
Параметризация решения
Для упрощения задачи форма решения фиксируется, т.е. желаемое решение параметризуется.
Предположим, что поведение переменной на входе \(x(t)\) нелинейного элемента периодично, а форма волны приблизительно гармоническая:
\ x(t)= A sin(\omega t)\
Анализ состояния сигнала
Предположим, что фильтр принимает гармоническую форму желаемого периодического движения. Предположим, что амплитуды высших гармоник на входе и выходе нелинейной составляющей линейной части малы из-за фильтрующих свойств линейной части.
Другим необходимым условием метода является то, что влияние высших гармоник на состояние равновесия амплитуд и фаз невелико.
Подход 1. Передаточные функции
Следующим шагом является анализ потока гармонического сигнала через контур, состоящий из нелинейной части, линейной части и части сравнения. Предположим, что периодический сигнал на выходе нелинейного элемента
имеет тот же период, но может содержать высшие гармоники, которые также проходят через линейный компонент с передаточной функцией \(W(s)\), которая ослабляет их больше, чем компонент первой гармоники, в соответствии с предположением фильтра. Исходя из этого, его вклад в переменную \(z(t)\) мал:
\z(t) = A_z sin(\omega t + \phi_z)\.
В случае отрицательной обратной связи, изменяющей фазу сигнала на \(-\pi\) радиан, условием наличия автоколебаний в контуре является баланс амплитуд и фаз:
\ A_z = A\\\\\\\\\phi_z = -\pi \\\\.
Тогда комплексный гармонический коэффициент усиления линейного компонента выражается следующим образом:
Аналогично, если преобразование гармонического сигнала из безынерционного нелинейного компонента описывается комплексным коэффициентом передачи (функцией описания):
где \(R_n(A)\) — отношение амплитуды первой гармонической составляющей сигнала \(y(t)\) к амплитуде \(A\) входного сигнала; \(\phi_n(A)\) — сдвиг фазы первой гармоники относительно входного сигнала.
Когда гармонический сигнал проходит через последовательно соединенные нелинейный элемент и линейный компонент, его амплитуда изменяется в \(R(\omega)R_n(A)\) раз, а сдвиг фазы равен \(\phi(\omega)+\phi(A)\).
В этой нелинейной системе периодическое колебание может возникнуть, если амплитуда гармонического сигнала при прохождении через контур сохраняется, а сдвиг фаз с элементом сравнения составляет \(- \pi \), т.е. выполняются следующие условия:
\ phi_n(A) + \phi(\omega) = -\pi\.
Подход 2. Критерий Найквиста
Мы можем определить условия возникновения автоколебаний другим способом.
Далее мы представляем структурную схему гармонической линеаризованной системы, соответствующей исходной системе для набора гармонических сигналов на входе нелинейного элемента при выполнении предположения о фильтре.
Особенностью такой модели является неполнота ее параметров, которые зависят от требуемой амплитуды \(A\) и частоты \(\omega \). Автоколебания возможны в исходной системе, если в эквивалентной системе обнаружены гармонические колебания, т.е. параметры линеаризованной системы соответствуют границе устойчивости колебаний. Согласно критерию Найквиста, условие нахождения значений параметров линеаризованной системы, задаваемых частотными характеристиками звеньев, в пределе устойчивости выражается следующим образом:
Источник
- Теория автоматического управления: Учеб. для вузов/С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б. Яковлева. — М.: Высшая школа, 2003. — 567 с.
- Автоколебания. Введение
- Автоколебания. Гармоническая линеаризация
- Автоколебания. Определение параметров периодических режимов
- Автоколебания. Устойчивость
This entry was posted on 06/02/2018 by Александр Синица in Теория автоматического управления and tagged Автоколебания.
Автоколебания в технике
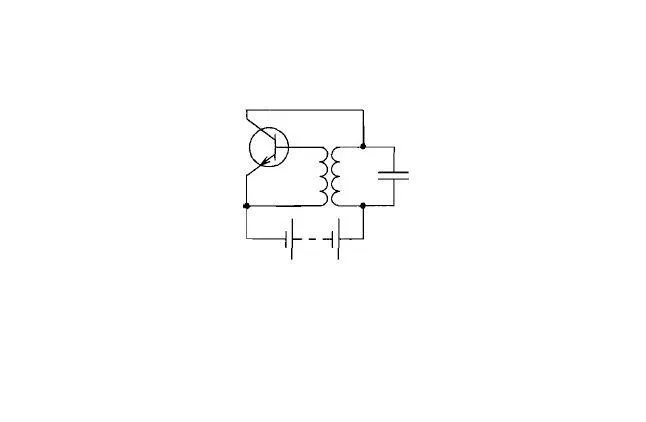
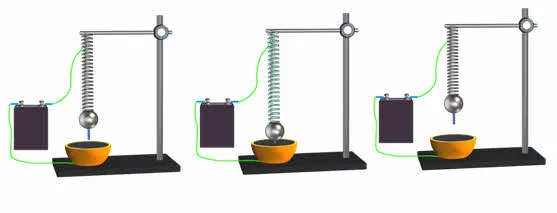
Автоматическая система колебаний с задержкой (на примере электромеханического звонка) Рассмотрим пример электромеханического звонка:
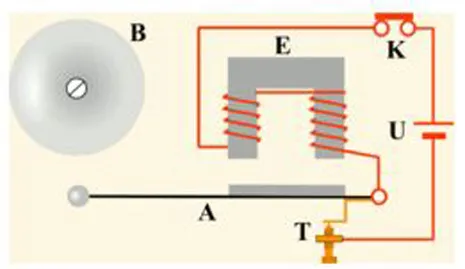
Когда кнопка (K) замыкает цепь, электромагнит (E) притягивает стреляющий штифт, стреляющий штифт ударяет в колокол и размыкает цепь электромагнита, механически соединенный контакт (T) оттягивает стреляющий штифт (A), и процесс повторяется.
Рассматривая процесс возникновения автоколебаний, мы предполагаем, что сила, действующая на ударный колокол (A), изменяется с изменением тока в цепи RL.
Это предположение служит для упрощения исследования, так как зависимость силы от тока в обмотке и от расстояния между бойком и полюсами гораздо сложнее, чем 3.
Ниже приведены чертежи электромеханических колоколов и их упрощенная схема:
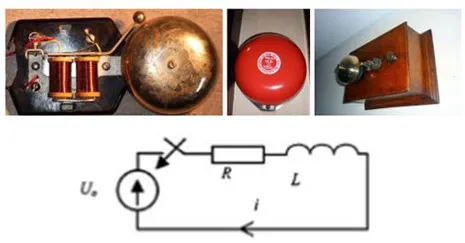
Плунжер колеблется относительно заданного зазора в соответствии с соотношением A*sin (w*t). Численно решая дифференциальное уравнение цепи RL с начальными условиями для замыкания и размыкания контакта и накладывая колебания толкателя на эти решения, мы получаем:
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=100;L=0.07;E=100;tm=L/R;T=0.0280;w=2*np. pi/T # параметры цепи RL и частота скачков w def dydt(y, t):# функция дифференциального уравнения для численного решения retur n-y/tm def dydt1(y1, t): retur n-y1/tm+E/L plt. title('Колебательные процессы в колоколе', size=12) y = odeint(dydt, E/R, np.linspace(0,T/4,300))# ток (сила) при открытии РЛ, y(0)=E/R plt. plot(np.linspace(0,T/4,300), y,'b',linewidth=2,label='Сила Fp=Km*Ip')# график y1 = odeint(dydt1, 0, np. linspace(T/2,3*T/4,300))# ток (сила) при закрытии РЛ, y(0)=0 plt.plot( np.linspace(T/2,3*T/4,300), y1,'g',linewidth=2,label='сила Fz=Km*Iz') t2=np. linspace(0,T,300) y2=(E/R)*np.sin(w*t2)# уравнение ударных колебаний plt.plot(t2, y2,"--r",linewidth=2,label='ударные колебания ') t3=np. linspace(0,T/4,300) t4=np.linspace(T/2,3*T/4,300) y3=0 for i in t3 y4=0 for i in t4 plt.plot(t3, y3,"--k",linewidth=3,label='Fp lag from striker ') plt. plot(t4, y4, "--k",linewidth=3,label='отставание Fz от ударника') plt.legend(loc='best') plt.grid(True) plt.show()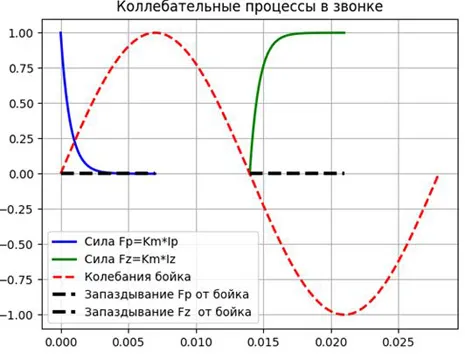
Для приближенной теории мы предполагаем, что сила Fτ выражается в виде последовательности квадратных импульсов, которые появляются и исчезают мгновенно, но не в момент активации контакта, а с задержкой t=L/R. Если мы добавим Fτ к графику, то получим:
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=100;L=0.07;E=100;tm=L/R;T=0.0280;w=2*np.pi/T # параметры цепи RL и частотного бойка w def dydt(y, t):# diff. Функция уравнения для численного решения retur n-y/tm def dydt1(y1, t): retur n-y1/tm+E/L plt.title('Вибрационные процессы в ударнике', size=12) y = odeint(dydt, E/R, np. linspace(0,T/4,300))# ток (сила) при открытии РЛ, y(0)=E/R plt. plot(np.linspace(0,T/4,300), y,'b',linewidth=2,label='Сила Fp=Km*Ip')# график y1 = odeint(dydt1, 0, np. linspace(T/2,3*T/4,300))# ток (сила) при закрытии РЛ, y(0)=0 plt.plot( np. linspace(T/2,3*T/4,300), y1,'g',linewidth=2,label='Сила Fz=Km*Iz') t2=np. linspace(0,T,300) y2=(E/R)*np.sin(w*t2)# уравнение ударной вибрации plt.plot(t2, y2,'--r',linewidth=2,label='ударная вибрация') def con_n(f): z=0 if np.sin(0)<=np.sin(f)
Химические колебания. Брюсселятор
Важным и нетривиальным примером самопульсирующих процессов являются некоторые химические реакции. Химические колебания - это колебания концентраций реагирующих веществ.
На сегодняшний день известно несколько осциллирующих реакций. Самый известный из них был открыт Б.П. Белоусовым в 1950 году и впоследствии подробно изучен А.М. Жаботинским. Реакция Белоусова-Жаботинского (БЖ) - это процесс окисления малоновой кислоты путем взаимодействия в присутствии ионов в качестве катализатора.
В ходе реакции раствор периодически меняет цвет: синий - красный - синий - красный и т.д. Помимо простых периодических колебаний, реакция BG демонстрирует множество различных типов пространственно-временной динамики (в зависимости от экспериментальных условий), которые еще окончательно не изучены.
Было предложено несколько математических моделей для реакции BL (например, модель "Oregonator" Филда, Кереса и Нойеса), но ни одна из них не описывает полностью все детали, наблюдаемые в эксперименте.
Рассмотрим более простой пример модели: гипотетическую химическую реакцию под названием "Брюсселятор 8". Уравнения для этой реакции имеют вид:

Предполагается, что реагенты A и B находятся в избытке, поэтому их концентрации можно считать постоянными, а D и E не участвуют ни в какой реакции. Составим кинетические уравнения, соответствующие реакции и описывающие динамику концентраций реагирующих веществ.
Поскольку количество энергии химической реакции в единицу времени определяется вероятностью столкновения реагирующих молекул, скорость изменения концентрации продуктов реакции пропорциональна произведению концентраций соответствующих реактантов и коэффициентов пропорциональности, так называемых констант скорости реакции. Тогда кинетические уравнения можно записать в виде:
Символы Y, X теперь обозначают соответствующие концентрации. Из третьего уравнения системы следует, что скорость образования вещества Х зависит от его концентрации, т.е. эта часть реакции является автокаталитической. Сведем уравнения (1) к безразмерной форме, содержащей минимальное количество управляющих параметров. Для этого мы вводим новые переменные, чтобы уравнения (1) приняли вид:

Построим фазовые портреты для: a=1.0; b=2.1; b=3.0; b=5.0
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt b=2.1 def f(y, x): y1, y2 = y return 1-(b+1)*y1+(y1**2)*y2, b*y1-(y1**2)*y2 x= np. linspace(0,100,1001) y0 = 0.5,1.5 y1,y2=odeint(f, y0, x).T plt .plot(y1,y2,linewidth=2,label='a=1.0, b=%s'%b) plt.legend(loc='best') plt .grid(True) plt.show()
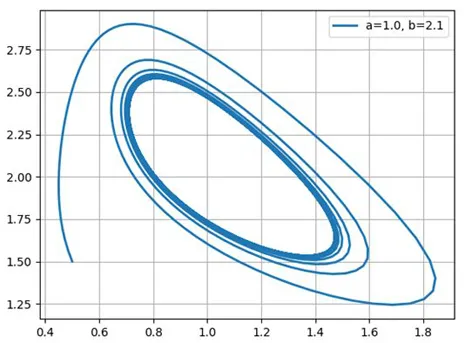
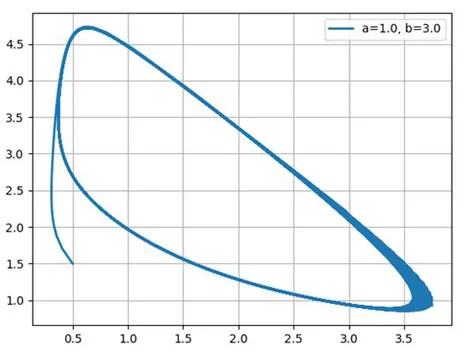
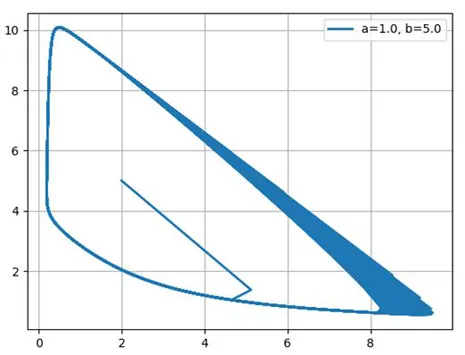
Таким образом, химический осциллятор демонстрирует поведение, типичное для автоколебательных систем и очень похожее, например, на осциллятор Ван дер Поля.
Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)
В динамике популяций есть много примеров, когда изменение популяции во времени имеет колебательный характер. Одним из наиболее известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтера-Лотки.
Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x и y— число жертв и хищников соответственно. Предположим, что относительный прирост жертв y'/x равен a-by, a>0, b>0, где α - коэффициент воспроизводства жертв в отсутствие хищников - с потерями из-за хищников.
Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x=0 ) относительная скорость изменения популяции хищников равна y'/y =-c, c>0, наличие пищи компенсирует убывание, и при x>0 имеем y'/y =(-c +d*x), d>0.
Таким образом, система Вольтерра-Лотки имеет вид:
Рассмотрим фазовый портрет системы Вольтерра-Лотки для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x(0)=3, y(0)=1, построенные с помощью программы Python для численного решения системы обыкновенных дифференциальных уравнений:
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt a=4;b=2.5; c=2; d=1 def f(y, t): y1, y2 = y return y1*(a-b*y2),y2*( -c+d*y1) t = np. linspace(0,10,201) y0 = 3, 1 y1,y2=odeint(f, y0, t).T plt.figure() plt .plot(y1,y2,linewidth=2) plt .grid(True) plt.figure() plt .plot(t,y1,linewidth=2) plt .plot(t,y2,linewidth=2) plt .grid(True) plt.show()
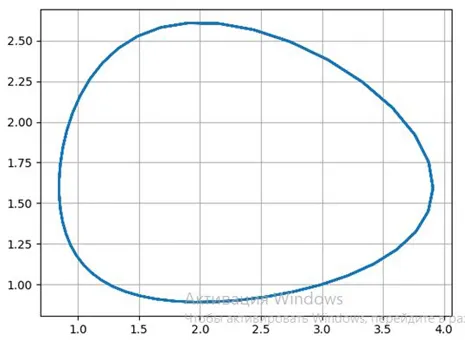
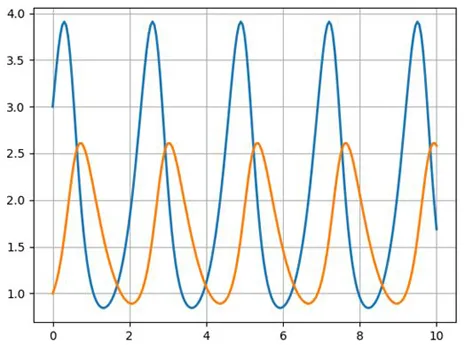
Мы видим, что процесс колеблется. При заданном начальном соотношении популяций 3:1 обе популяции изначально увеличиваются. Когда число хищников достигает b=2,5, популяция жертв не успевает восстановиться, и число жертв начинает снижаться.
Через некоторое время снижение количества пищи начинает сказываться на популяции хищников, и когда популяция добычи достигает x=c/d=2 (в этот момент y'=0), количество хищников также начинает снижаться по мере уменьшения популяции добычи. Популяция уменьшается, пока число хищников не достигнет y=a/b =1,6 (в этот момент x'=0).
Через некоторое время появляется достаточно пищи, чтобы поддержать рост численности хищников, обе популяции увеличиваются и ... процесс повторяется снова и снова.
Рассматриваемая модель может описывать поведение конкурирующих компаний, рост населения, численность военных армий, изменения окружающей среды, развитие науки и т.д.








