Начальная фаза на диаграмме колебаний соответствует точке на кривой колебаний в момент времени t=0. На рисунке также есть маленькая красная точка, соответствующая начальной фазе колебаний.
Частная школа. 9 класс
Эскиз урока физики в 9 классе по теме «Период и частота». Какова продолжительность периода вращения? Какова частота вращения? Как вычислить скорость и ускорение тела, движущегося по окружности, если известны период и частота вращения?
Измерить скорость тела, движущегося по кругу, не всегда просто. Однако его можно рассчитать, используя такие понятия, как период и частота.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, движение повторяется снова и снова через равные промежутки времени. Примером может служить движение на обычной детской карусели.
Время, за которое тело совершает полный оборот, называется периодом вращения. Продолжительность вращения обычно обозначается буквой T. Единицей измерения этой физической величины в СИ является секунда.
Вы узнали о понятии «период революции» во время изучения географии. Земля, например, имеет период вращения 23 часа, 56 минут и 4 секунды и обращается вокруг Солнца за 1,00004 земных года. Планета Меркурий имеет самый короткий орбитальный период вокруг Солнца в нашей Солнечной системе. Его орбитальный период составляет 0,24085 земных лет. Интересно, что самая большая планета в нашей Солнечной системе, Юпитер, имеет самый короткий орбитальный период — всего 9 часов 50 минут. Орбитальный период Солнечной системы вокруг галактического ядра оценивается в 226 000 000 лет.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по своей окружности, называется орбитальной частотой. Частота вращения обозначается греческой буквой n.
Если при катании на карусели в парке мы делаем один оборот за 20 секунд, то продолжительность оборота в этом случае составляет T = 20 секунд. Как мы можем определить частоту этого движения? Сколько оборотов совершает карусель за 1 секунду?
Очевидно, что n = 1/T = 1/20 1 /с, т.е. за 1 с карусель совершает одну двадцатую часть полного оборота.
Таким образом, частота обращения является обратной величиной длительности обращения:
Поэтому единицей измерения этой физической величины является обратная величина секунды, т.е. 1 /с или с-1 .
Что такое амплитуда
Амплитуда — это наибольшее отклонение величины от равновесия, т.е. максимальное значение колеблющейся величины.
Она измеряется в тех же единицах, в которых измеряется колеблющаяся величина. В случае механических колебаний, когда изменяется координата, амплитуда измеряется, например, в метрах.
Для электрических колебаний, при которых изменяется заряд, он измеряется в кулонах. В случае колебаний тока он измеряется в амперах, в случае напряжения — в вольтах.
Часто его указывают, добавляя «0» под буквой, обозначающей амплитуду.
Например, пусть величина \( \large x \) колеблется. Тогда символ \( \large x_ \) обозначает амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используется латинская заглавная буква A, поскольку она является первой буквой английского слова «amplitude».
Для определения амплитуды можно использовать диаграмму, как показано на рисунке 2:
Рисунок 2. Амплитуда — это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через нулевую плоскость оси, на которой находится амплитуда
Что такое период
При точном повторении колебаний изменяющаяся величина принимает те же значения через тот же промежуток времени. Такой промежуток времени называется периодом.
Обычно он обозначается латинской заглавной буквой «T» и измеряется в секундах.
\( \big T \left( c
ight) \) — период колебаний.
Секунда — это относительно длительный период времени. Поэтому, хотя период измеряется в секундах, для большинства колебаний он измеряется долями секунды.
Чтобы определить период по диаграмме колебаний (рис. 3), найдите два одинаковых значения колеблющейся величины. Затем нарисуйте штрихи от этих значений на оси времени. Расстояние между штрихами — это период колебаний.
Рисунок 3. Период колебаний — это горизонтальное расстояние между двумя одинаковыми точками на графике.
Период — это время одного полного колебания.
На графике проще всего найти период одним из следующих способов (рис. 4):
Что такое частота
Рисунок 4. Удобно определить период как расстояние между двумя соседними пиками или между двумя долинами.
Удобно использовать греческую букву «ню» для обозначения периода, когда период находится между двумя точками или между двумя точками в линии. \( \great
u \).
Частота отвечает на вопрос: «Сколько полных колебаний происходит за одну секунду?». Или: «Сколько периодов помещается в интервал времени, равный одной секунде?».
Поэтому размерность частоты — это единица колебаний в секунду:
\( \big
u \left( \frac
ight) \).
В учебниках его иногда называют \( \large \displaystyle
u \links( c^
Колебания в природе
ight) \), потому что по свойствам степени \( \large \displaystyle \frac = c^ \).

С 1933 года частота записывается в герцах в честь Генриха Рудольфа Герца. Он сделал важные открытия в физике, изучил колебания и доказал существование электромагнитных волн.
Маятник
Одно колебание в секунду соответствует частоте в 1 герц.
Чтобы определить частоту на диаграмме, необходимо определить период на оси времени. Затем рассчитайте частоту по этой формуле:
Частота колебаний
Существует и другой способ определения частоты с помощью диаграммы колеблющейся величины. Отмерьте на диаграмме временной интервал в одну секунду и подсчитайте количество периодов колебаний, укладывающихся в этот интервал (см. рис. 5).
Рисунок 5. Частота на диаграмме — это количество периодов, укладывающихся в одну секунду.
Вариации разной величины очень часто встречаются в природе. Явление осцилляции заключается в том, что измеряемая величина изменяет свое значение вокруг среднего значения.
Колебания могут быть периодическими (маятник) или непериодическими (флаг на ветру). Поскольку каждое непериодическое колебание может быть представлено в виде бесконечной суммы периодических колебаний, сначала рассматриваются периодические колебания. График этих колебаний представляет собой кривую синуса, которая хорошо изучена в математике.
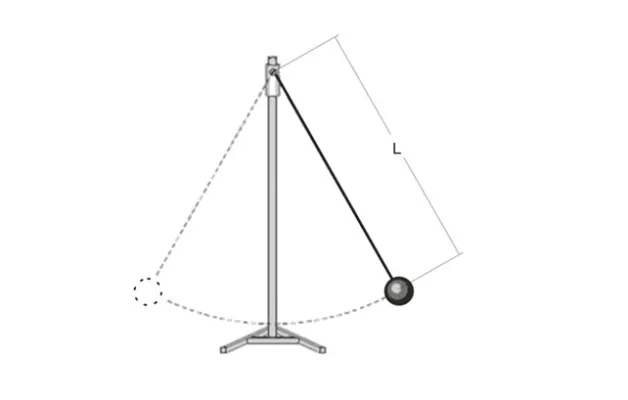
Для изучения основных понятий колебательных процессов подходящим примером является маятник — небольшая масса, подвешенная на тонкой, легкой нити. Когда вы встряхиваете его, он начинает совершать регулярные движения.
- N – число колебаний;
- t – время, за которое эти колебания были совершены (сек).
Любое движение маятника, которое начинается из одной конечной точки и заканчивается в той же точке, называется колебанием.
Если вы возьмете несколько маятников разной длины, то обнаружите, что они качаются с «разными скоростями» (хотя линейная скорость гири может быть одинаковой). То есть, «скорость колебаний» и скорость движения груза маятника — не одно и то же.
Математический маятник
Для описания «скорости колебаний» используется специальный термин — частота колебаний.
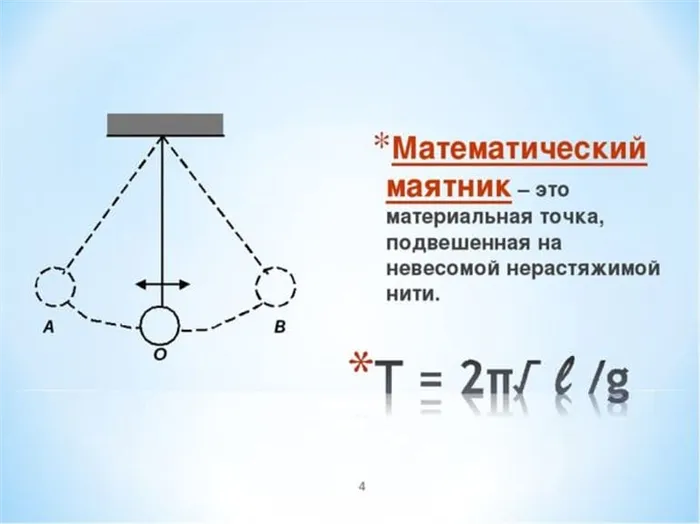
Количество колебаний, происходящих в единицу времени, называется частотой колебаний. Для этого используется греческая буква $
u$ («ню»).
Единицей частоты колебаний в системе СИ является герц (Гц). Один герц — это количество колебаний, происходящих за одну секунду.
Для измерения частоты колебаний подсчитывают количество колебаний за определенный период времени и делят его на длину периода:

В этой формуле размер колебаний не имеет значения, только их количество.
Диапазон частот, воспринимаемых непосредственно человеком, составляет от примерно 10^$ Гц (частота движения планет вокруг Солнца) до 20 кГц (самый высокий тон). Частоты до $10^$ Гц (жесткое гамма-излучение) используются в сельском хозяйстве и технике.
Таким образом: -gx/l=-(ω)^2x ->Эта модель рассматривает движение груза, подвешенного на струне. Она описывает систему, в которой масса струны намного меньше массы груза, а ее длина намного больше ее размеров.
Кроме того, шнур должен быть невесомым и нерастяжимым.
В этом случае нагрузка считается материальной точкой.
При соблюдении этих условий частота колебаний маятника и период не зависят от массы груза. Рассматривается движение математического маятника при малом угле отклонения (a). Последняя измеряется в радианах и поэтому приблизительно соответствует значению углов синуса и тангенса. Этот же угол пропорционален отношению между прогибом и длиной струны:
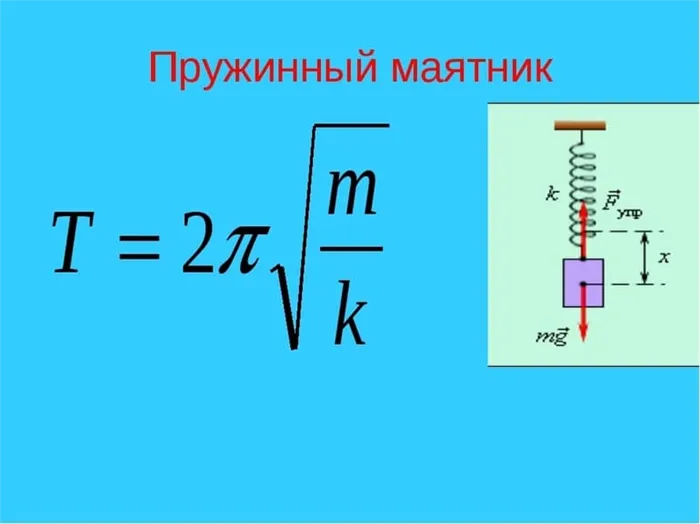
Пружинный маятник
α=x/l .

На маятник воздействует синусоидальная составляющая силы тяжести и тангенциальная сила натяжения струны. Согласно второму закону Ньютона: ma=-mgsin (a). Это дает a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
ω ^2=г/л.
Период.
Это формула Галилея, описывающая движение математического маятника.
Формула для частоты колебаний математического маятника: v=sqrt (l/g)/2π .
Аналогичный термин относится к системе, в которой груз, подвешенный на легкой пружине, совершает движение.
Явление резонанса
Тело находится в положении равновесия, когда пружина не деформирована. Если его растянуть или сжать, система начинает раскачиваться под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна перемещению тела (x), но направлена в противоположную сторону. Коэффициент пропорциональности между этими двумя величинами называется жесткостью пружины (k):
F=-kx .
Пружинный маятник
α=x/l .

На маятник воздействует синусоидальная составляющая силы тяжести и тангенциальная сила натяжения струны. Согласно второму закону Ньютона: ma=-mgsin (a). Это дает a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
ω ^2=г/л.
Период.
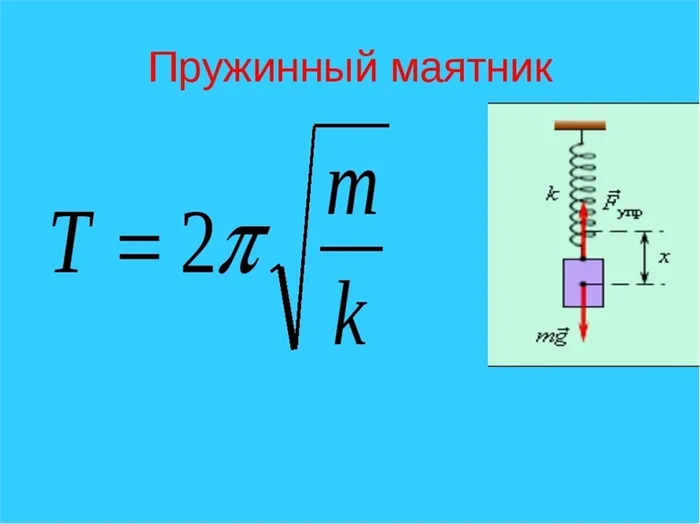
Это формула Галилея, описывающая движение математического маятника.
Формула для частоты колебаний математического маятника: v=sqrt (l/g)/2π .
Аналогичный термин относится к системе, в которой груз, подвешенный на легкой пружине, совершает движение.
Явление резонанса
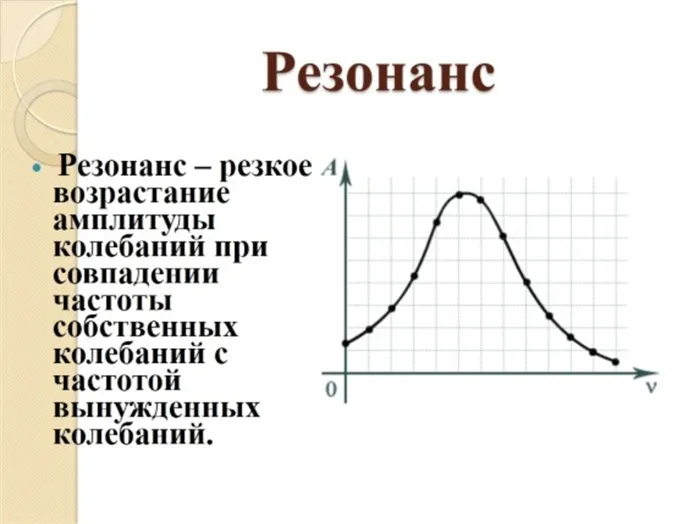
Тело находится в положении равновесия, когда пружина не деформирована. Если его растянуть или сжать, система начинает раскачиваться под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна перемещению тела (x), но направлена в противоположную сторону. Коэффициент пропорциональности между этими двумя величинами называется жесткостью пружины (k):
F=-kx .
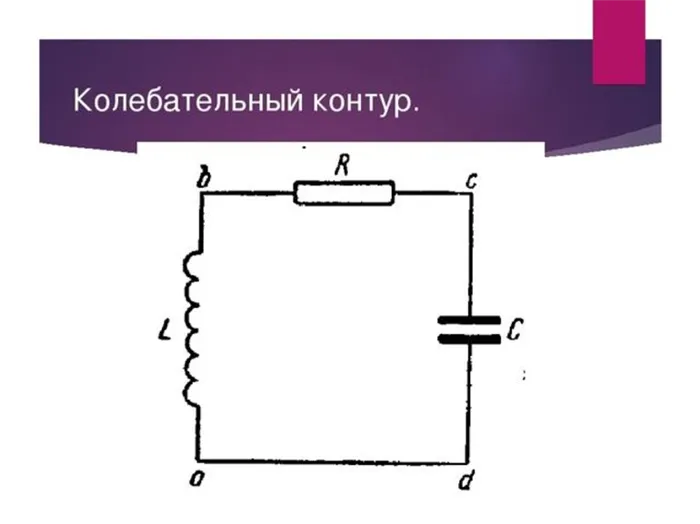
Колебательный контур
Сила упругости достигает своего максимального значения в точке наибольшего отклонения тела (амплитуда, смещение) от равновесия. В этот момент ускорение также больше.
Когда тело приближается к положению равновесия, сила упругости и ускорение уменьшаются. В середине обе величины равны нулю, но скорость тела имеет ненулевое значение. Поэтому вес не останавливается, а продолжает двигаться.
После прохождения положения равновесия он движется в обратном направлении по инерции и под действием силы упругости тянется назад. Трение воздуха уменьшает скорость, и маятник останавливается.
Все эти модели могут быть связаны с классическим гармоническим осциллятором — системой с одной степенью свободы, описываемой одним уравнением.
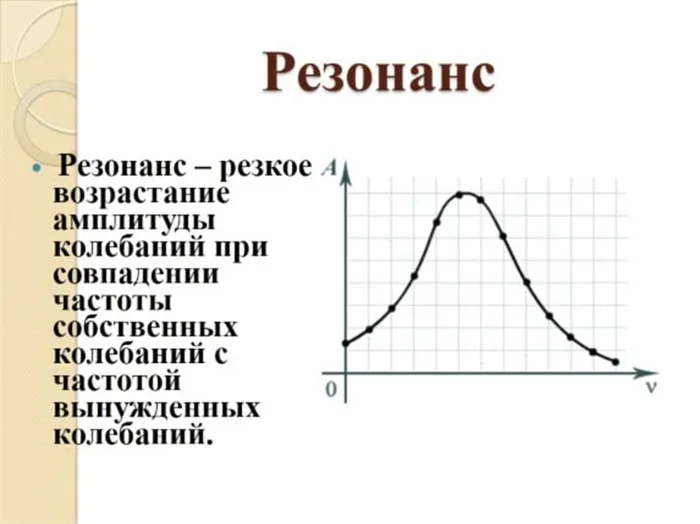
Эта концепция имеет особое значение для описания колебаний. Если возникает возмущение, частота которого приближается к собственной частоте системы, система реагирует резким увеличением амплитуды.
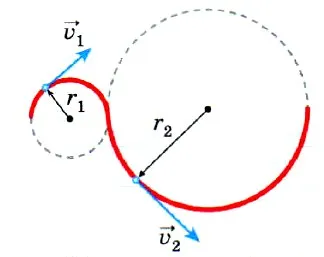
Эффект резонанса можно представить на примере того же математического маятника. Для этого привяжите маятник к нити, к которой прикреплен другой такой же маятник, но с более длинной нитью. Длину нити второго маятника можно регулировать. Если привести в движение оба маятника и постепенно изменять длину второй струны, то можно заметить, что амплитуда увеличивается по мере приближения размеров обеих струн.
Явление резонанса
Тело находится в положении равновесия, когда пружина не деформирована. Если его растянуть или сжать, система начинает раскачиваться под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна перемещению тела (x), но направлена в противоположную сторону. Коэффициент пропорциональности между этими двумя величинами называется жесткостью пружины (k):
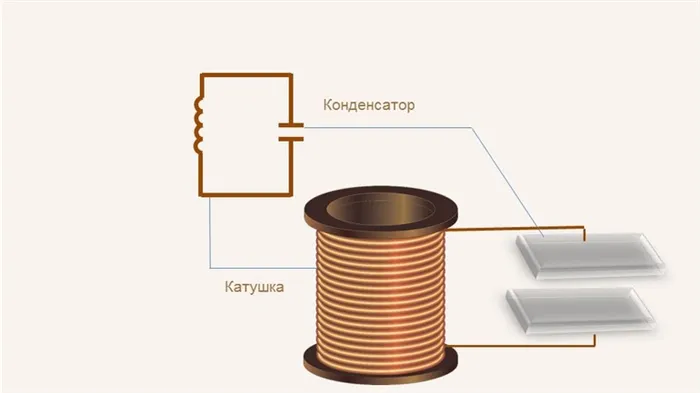
В простейшем примере это замкнутый контур, состоящий из индукционной катушки и конденсатора. При определенных условиях в такой цепи могут генерироваться и поддерживаться электрические колебания.
F=-kx .
Свет
Конденсатор разряжается индукционной катушкой, и в цепи возникает ток, сила которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.
Длина волны и цвет
Электрический заряд конденсатора преобразуется в магнитное поле. Затем магнитное поле катушки уменьшается, и конденсатор снова заряжается. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: Частота, амплитуда и период.
Они свободны и амортизированы. Для их поддержания необходимо регулярно заряжать конденсатор.
Эта концепция имеет особое значение для описания колебаний. Если возникает возмущение, частота которого приближается к собственной частоте системы, система реагирует сильным увеличением амплитуды.
Явление резонанса также можно представить на примере математического маятника. Для этого нужно привязать маятник к нити, к которой прикреплен другой такой же маятник, но с более длинной нитью. Длину нити второго маятника можно регулировать. Если привести в движение оба маятника и постепенно изменять длину второй струны, то можно заметить, что амплитуда увеличивается по мере приближения размеров обеих струн.
Отражение света
Читайте также: Резонансный контур LC: принцип работы, расчет, определение
В этом случае первый маятник является приемником колебаний, а второй маятник — передатчиком. Причиной увеличения амплитуды является колебание маятника с той же частотой.
Видимый свет — это электромагнитные волны с частотой и длиной, которые определяют его цвет.
Спектроскопия
Самая короткая длина волны видимого света составляет 380 нанометров. Это фиолетовый цвет, за ним следует синий и голубой, затем зеленый, желтый, оранжевый и, наконец, красный. Белый свет состоит из всех цветов одновременно, что означает, что белые объекты отражают все цвета. Это можно увидеть с помощью призмы. Падающий свет преломляется и выстраивается в полосу цветов в том же порядке, что и радуга. Порядок — от цветов с наименьшей длиной волны к цветам с наибольшей длиной волны. Зависимость скорости распространения света через вещество от длины волны называется рассеянием.
Звук
Радуга над рекой Ниагара
Радуга формируется аналогичным образом. Капельки воды, рассеянные в атмосфере после дождя, действуют как призма и преломляют каждую волну. Цвета радуги настолько важны, что во многих языках существуют мнемоники — методы запоминания цветов радуги, которые настолько просты, что их могут запомнить даже дети. Многие дети, говорящие по-русски, знают, что «каждый охотник хочет знать, где сидит фазан». Некоторые люди придумывают свои собственные мнемоники, и это особенно полезное упражнение для детей, потому что если они придумают свой собственный способ запомнить цвета радуги, они смогут запомнить их быстрее.
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Свет, к которому человеческий глаз наиболее чувствителен, — зеленый, с длиной волны 555 нм при ярком свете и 505 нм в сумерках и на рассвете. Не все животные чувствительны к цвету. У кошек, например, не развито цветовое зрение. С другой стороны, некоторые животные видят цвета гораздо лучше, чем люди. Например, некоторые виды могут видеть ультрафиолетовый и инфракрасный свет.
Цвет объекта определяется длиной волны света, отраженного от его поверхности. Белые объекты отражают все волны видимого спектра, а черные объекты поглощают все волны и ничего не отражают.
На первом рисунке: бриллиант обычной огранки. Свет отражается вверх к глазу, и бриллиант сияет. На втором и третьем рисунке: неровный срез. Свет отражается на оправе и на гранях, и бриллианты выглядят тусклыми.
Природным материалом с высоким коэффициентом дисперсии является алмаз. Правильно обработанные бриллианты отражают свет как снаружи, так и изнутри, преломляя его подобно призме. Важно, чтобы большая часть этого света отражалась вверх, к глазу, а не вниз, вглубь помещения, где он не виден. Благодаря высокой дисперсии бриллианты прекрасно блестят на солнце и при искусственном освещении. Стекло, ограненное таким же образом, как и алмаз, тоже блестит, но не так сильно. Это связано с тем, что бриллианты отражают свет гораздо лучше, чем стекло, благодаря своему химическому составу. Углы, используемые при огранке алмазов, имеют большое значение, поскольку слишком острые или слишком тупые углы либо препятствуют отражению света от внутренних стенок, либо отражают свет в оправу, как показано на рисунке.
Спектральный анализ или спектроскопия иногда используется для определения химического состава вещества. Этот метод особенно полезен, когда химический анализ вещества не может быть выполнен путем прямой обработки, например, при определении химического состава звезд. Если вы знаете, какое электромагнитное излучение поглощает тело, вы можете определить, из чего оно состоит. Абсорбционная спектроскопия, отрасль спектроскопии, определяет, какое излучение поглощается телом. Этот вид анализа можно проводить дистанционно, поэтому он часто используется в астрономии и при работе с токсичными и опасными веществами.
Звук — это вибрация резиновой среды, воспринимаемая органом слуха.
Условия, необходимые для возникновения и восприятия звука:
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
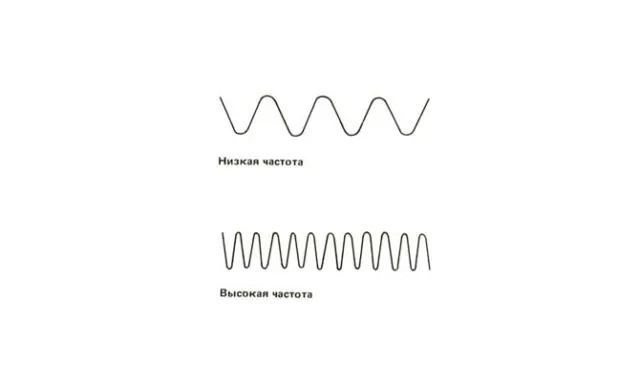
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Звуковые волны — это упругие волны, которые вызывают у человека ощущение звука, будучи полосами сжатия и разрежения, передаваемыми на определенное расстояние в течение определенного времени.








