Горизонт в астрономии это. Горизонт в астрономии это.

Содержание

Номограмма Струйского (Рисунок 3) используется для приблизительной оценки видимости объектов: Точки, соответствующие высоте точки наблюдения и высоте объекта, отмечаются на двух крайних шкалах номограммы, затем через них проводится линия, и видимость объекта получается при пересечении этой линии со средней шкалой 14.

Заглянуть за горизонт

В словаре 1910 года горизонт определяется как «окружность круга, за которой ничего не видно». Однако в прошлом веке наука расширила эту концепцию до масштабов Вселенной.

Обычный оптический горизонт, который зависит от сферической формы нашей планеты, статичен и не зависит от времени наблюдения (более того, он не учитывает конечную скорость света на расстояниях в километры). Однако в применении к Вселенной понятие горизонта теряет свою былую простоту. Космическое пространство не двухмерное, как рельеф Земли, а трехмерное; более того, Вселенная расширяется, причем с разной скоростью. Кроме того, для космических масштабов необходимо учитывать конечную скорость света.

Два горизонта

Концепция космологического горизонта была введена в научный оборот в начале 1950-х годов с развитием теории горячей Вселенной. Великий специалист по ГТР Вольфганг Риндлер из Корнельского университета объяснил и расширил эту концепцию в своей работе 1956 года «Визуальные горизонты в моделях мира». Риндлер предложил различать долгоживущие космические объекты, такие как звезды и галактики, с их протяженными глобальными линиями (кривые в пространстве-времени, описывающие движение тела) и недолговечные явления, такие как взрывы сверхновых, которым соответствуют небольшие фрагменты таких линий, а на границе — простые точки. Наблюдаемость обоих типов объектов может быть правильно описана только различными горизонтами.

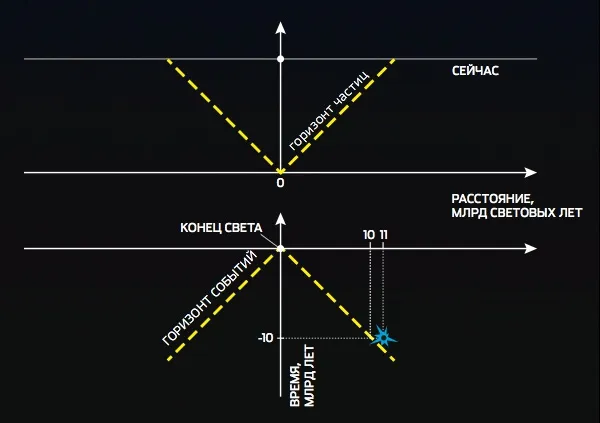
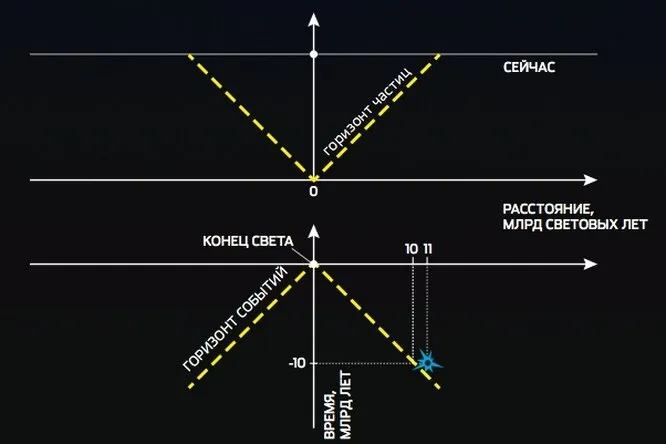
Простые горизонты Наблюдаемая часть (горизонт частиц) твердой Вселенной, имеющей начало, непрерывно расширяется со скоростью света. Во вселенной без начала, но с «концом света», где все линии мира прерываются, горизонт событий разделяет события, которые наблюдатель никогда не сможет увидеть.

Границу между наблюдаемой и ненаблюдаемой мировыми линиями Ридлер назвал горизонтом частиц, а аналогичную границу между точками на этих линиях — горизонтом событий.

Согласно стандартной космологической модели, мы живем в однородной, изотропной Вселенной. Из этого следует, что горизонт частиц представляет собой сферическую поверхность с наблюдателем в центре. Внутренняя часть сферы заполнена долгоживущими космическими объектами (например, галактиками), свет которых, испущенный в прошлом, достигает наблюдателя. На внешней стороне этой сферы находятся галактики, которые наблюдатель не может увидеть ни в один из периодов их истории до момента наблюдения. Таким образом, горизонт частиц отделяет наблюдаемую область Вселенной от ненаблюдаемой, т.е. по сути мало чем отличается от географического горизонта.

Горизонт событий, с другой стороны, менее ясен: он отделяет события, которые наблюдатель может увидеть в определенное время в своем будущем, от событий, которые он никогда не сможет увидеть. В некоторых космологических моделях существуют оба горизонта, в других — только один, а в третьих вообще нет горизонта.

Разные горизонты

Замкнутая, нестатичная фридмановская вселенная с положительной кривизной пространства возникает из точечной сингулярности с бесконечной плотностью энергии, достигает предельного размера в процессе расширения, затем сжимается и коллапсирует обратно в сингулярность. Такая вселенная имеет как горизонт частиц, так и горизонт событий.

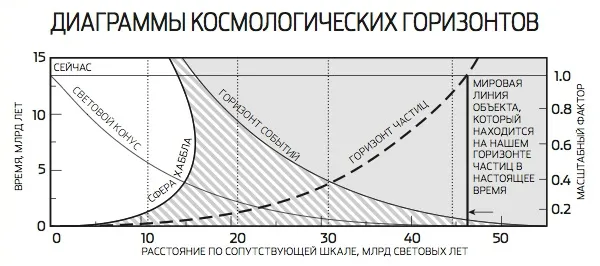
Вселенная Эйнштейна-Де Ситтера имеет горизонт частиц, но не имеет горизонта событий, поскольку скорость ее расширения со временем стремится к нулю, т.е. в бесконечно далеком будущем она становится статичной. Это также верно для любой открытой фридманновской вселенной, скорость расширения которой стремится к конечному ненулевому пределу в бесконечном будущем. Однако для «антигравитационной» вселенной де Ситтера, которая не имеет ни начала, ни конца, верно обратное: нет горизонта частиц, но есть горизонт событий.

Статичный мир

Для простоты рассмотрим горизонты бесконечной статической вселенной. В ньютоновском мире с бесконечной скоростью света (а значит, абсолютным временем), который не имеет ни начала, ни конца во времени, то есть существует вечно, наблюдатель, где бы он ни находился, всегда и без исключения может видеть все светящиеся тела. Поэтому в таком мире нет ни горизонта частиц, ни горизонта событий (ведь событий-то нет!) — он дважды без горизонта.

Теперь предположим, что сверхновые иногда взрываются в галактиках. Если скорость света бесконечна, то эти взрывы достигают наблюдателя мгновенно, поэтому двойной горизонт по-прежнему применим. Но это также применимо и для конечной скорости света!

Предположим, что яркость галактики кратковременно увеличивается в результате взрыва сверхновой. В вечной и статичной Вселенной свет от этой вспышки рано или поздно достиг бы каждого наблюдателя. Из этого следует, что в этом мире нет сигналов, которые наблюдатель никогда не сможет увидеть, и поэтому нет горизонта событий (конечно, нет и горизонта частиц).

Далее рассмотрим гипотетическую статическую вселенную с временным началом. В таком мире горизонт частиц представляет собой сферу, которая расширяется со скоростью света. Когда наблюдатель появится в одной из галактик через 5 миллиардов лет после сотворения этого мира, горизонт частиц будет представлять собой сферу с радиусом 5 миллиардов световых лет. Еще через миллиард лет радиус составит 6 миллиардов световых лет, а через 2 миллиарда лет — 7 миллиардов. Этот мир остается неизменным, но ощутимая его часть постоянно расширяется.

Наконец, предположим, что наша воображаемая статическая вселенная не имеет начала, но имеет конец, где все линии мира, включая линию наблюдателя, прерываются. Он по-прежнему видит все галактики, поэтому в этом мире нет горизонта частиц. Однако наблюдатель может наблюдать лишь часть изменений в яркости этих галактик. Он увидел бы взрыв сверхновой звезды в галактике, находящейся на расстоянии 10 миллионов световых лет от нас, если бы это произошло за 11 миллионов лет до конца света. Но если сверхновая взорвется за 9 миллионов лет до конца света, наблюдатель не узнает о ней до последнего момента ее существования — у него просто не останется времени. Поэтому в таком мире существует горизонт событий.

Какой бы примитивной ни была модель статической Вселенной, она позволяет нам понять основные особенности обоих горизонтов. За горизонтом частиц лежат универсальные линии, которые в любой момент времени нельзя наблюдать ни в одном из их предыдущих фрагментов. А за горизонтом событий происходят события, которые наблюдатель не может увидеть за все время их существования.

Видимый горизонт — это и линия, по которой небо, как кажется, демаркирует земную поверхность, и небесное пространство над этой демаркацией, видимая наблюдателю земная поверхность и все видимое вокруг наблюдателя пространство до его конечных пределов 2. Аналогичным образом понятие горизонта можно определить и для других небесных тел 3 .

Синонимы: Горизонт, горизонт, горизонт, небо, закатное небо, закатное небо, стекло, зреймо, вуаль, затвор, озор, овид, оглад, черта 4 .

Расстояние до видимого горизонта

Схематический чертеж для расчета расстояния до горизонта:

В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:

Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли 6. В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли. Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h 2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу 7 : где d и h в км. Ниже приведено расстояние до горизонта при наблюдении с различных высот 8 :

Высота над поверхностью земли h	расстояние от горизонта d	Пример точки наблюдения
1,75 м	4.7 км	стоя на земле
25 м	17.9 км	Здание 9 этажей
50 м	25,3 км	Колесо обозрения в парке аттракционов
150 м	43,8 км	Воздушный шар
2 км	159,8 км	Горный
10 км	357,3 км	Аэроплан
350 км	2114.0 км	Космический аппарат

Истинный горизонт

Истинный горизонт — это воображаемый большой круг небесной сферы, плоскость которого перпендикулярна перпендикуляру в точке наблюдения.

Синонимы: математический горизонт, астрономический горизонт 17 .

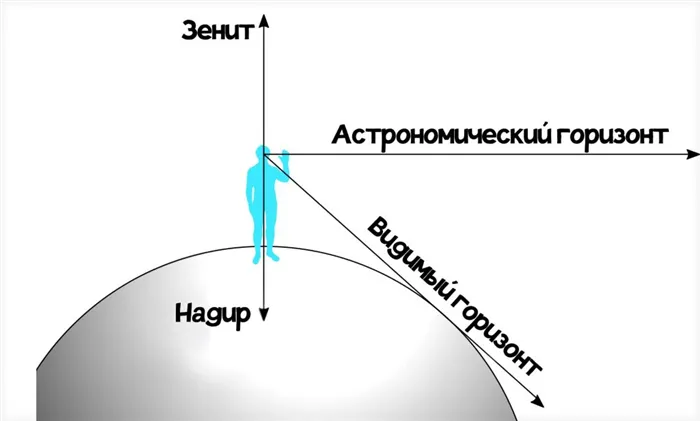
Искусственный горизонт — это инструмент, используемый для определения истинного горизонта.

Истинный горизонт можно легко определить, например, держа перед глазами стакан с водой так, чтобы уровень воды был виден как прямая линия 18 .

Примечания

↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М .: Транспорт, 1970. — 568 с.
↑ Словари и энциклопедии на Академике. Толкования выражения «видимый горизонт» .Архивировано из первоисточника 3 февраля 2012.
↑ Изучение Солнечной системы. Горизонт. Космос и астрономия .Архивировано из первоисточника 3 февраля 2012.
↑ Даль В. И. Толковый словарь живого великорусского языка. — М .: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8
↑ Цитата из песни на слова Михаила Анчарова «Стою на полустаночке». 1972.
↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М .: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7
↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М .: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3
↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости он-лайн .Архивировано из первоисточника 3 февраля 2012.
↑ Всё о космосе. Какой горизонт дальше? .Архивировано из первоисточника 3 февраля 2012.
↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М .: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614
↑ Климушкин Д. Ю.; Граблевский С. В. Космология. Космический горизонт (2001).Архивировано из первоисточника 3 февраля 2012.
↑ starpomlom Учебник судоводителя любителя. Глава VII. Навигация .
↑ Яхтенная энциклопедия. Видимый горизонт и дальность видимости .Архивировано из первоисточника 3 февраля 2012.
↑ Skeptic.net. Были ли американцы на Луне? .Архивировано из первоисточника 3 февраля 2012.
↑ Словари и энциклопедии на Академике. Толкования выражения «истинный горизонт» .Архивировано из первоисточника 3 февраля 2012.
↑ Запаренко Виктор Большая энциклопедия рисования Виктора Запаренко. — М .: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3

	Фото и видео Wikimedia Commons ?

Горизонт // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.

Географические термины
Системы небесных координат

Фонд Викимедиа. 2010 .

Полезное

Смотреть что такое «Горизонт» в других словарях:

горизонт — а, м. horizon m., нем. Horisont, гр. horizon. 1. Линия кажущегося соприкосновения неба с земной или водной поверхностью. СИС 1985. Оризонт. Черта, что с поверхности нашей земли умом нашим протягаяем во все стороны неба, сколь далеко глаз наш… … Исторический словарь галлицизмов русского языка
ГОРИЗОНТ — (греч. horizon, от horizo ограничиваю). 1) окружность круга, на котором небо кажется сливающихся с землей или с водой, и дальше которого уже ничего не видно, если смотреть на небо с моря или с обширной равнины, где ничто не препятствует видеть… … Словарь иностранных слов русского языка
Горизонт (КА) — Горизонт Характеристики Стартовая масса 2300±25 кг Изготовитель НПО ПМ Срок службы 3 лет Воспроизведение Количество транспондеров 6(C) 1(Ku) Мощность транспондера … Википедия
ГОРИЗОНТ — ГОРИЗОНТ, горизонта, муж. (греч. horizon). 1. только ед. Круговая линия, отделяющая в глазах наблюдателя видимое им небо от земной поверхности. Видимый горизонт. Истинный горизонт (см. истинный). Пароход скрылся за горизонтом. || Небосклон,… … Толковый словарь Ушакова
Горизонт — Морфон горизонтальной ориентации, выявляемый на всей ширине вскрытого земляной выработкой вертикального разреза почвы. Источник: ОСТ 56 81 84: Полевые исследования почвы. Порядок и способы проведения работ, основные требования к результатам … Словарь-справочник терминов нормативно-технической документации
горизонт — умственный горизонт. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. горизонт ширь, кругозор, окоем, интересы, пропласток, круг интересов, глей, глазом не окинуть, даль, простор,… … Словарь синонимов
Горизонт — 1. Г. с географическим назв. стратиграфическая единица регионального значения, объединяющая по горизонтали (на площади) разнофациальные синхроничные отл., примерно соответствующие по рангу зоне единой шкалы. Г. выделяется по палеонтологическим… … Геологическая энциклопедия
Горизонт — 1) Горизонт видимый линия, по которой небо кажется граничащим с поверхностью земли. 2) Горизонт истинный (математический) большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии и проходит через глаз наблюдателя. 3)… … Морской словарь
горизонт B — Почвенный горизонт, в котором накапливаются вещества, вынесенные из вышележащих (элювиальных) горизонтов почвы. Syn.: иллювиальный горизонт; горизонт вмывания … Словарь по географии
горизонт А — Горизонт в верхней части почвенного профиля, из которого вынесены в более глубокие горизонты или за пределы профиля растворимые вещества и илистые частицы. Syn.: элювиальный горизонт; горизонт вымывания … Словарь по географии
ГОРИЗОНТ — (от греч. horizon род. п. horizontos, букв. ограничивающий), кривая, ограничивающая часть земной поверхности, доступную взору (видимый горизонт). Видимый горизонт увеличивается с высотой места наблюдения и обычно расположен ниже истинного (в… … Большой Энциклопедический словарь

Сколько километров до горизонта?

Предположим, что наблюдатель находится на плоской поверхности Земли, и перед ним нет никаких препятствий. Что ограничивает обзор? Ответ прост: геоидная форма планеты. В определенной точке изогнутая поверхность Земли обычно пересекает линию горизонта. Поэтому наблюдатель не может видеть ничего дальше.

Даже специальное оптическое устройство не может исправить эту ситуацию. С помощью бинокля, например, можно гораздо четче рассмотреть предметы, находящиеся на большом расстоянии. Однако невозможно пересечь линию горизонта и «заглянуть за горизонт».

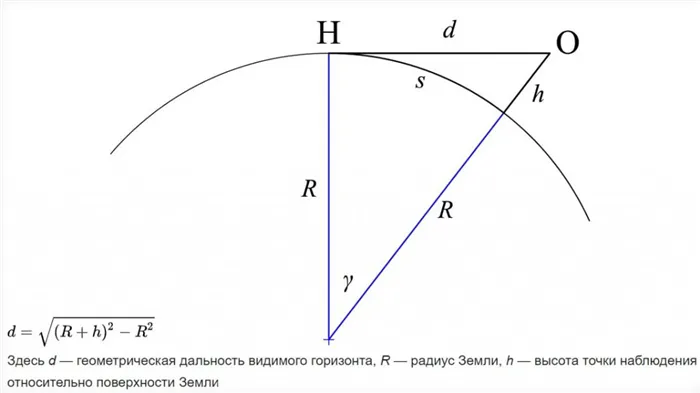
Можно ли рассчитать, сколько километров до горизонта? Если представить ее как линию между небом и землей, то можно использовать теорему Пифагора для расчета геометрического расстояния.

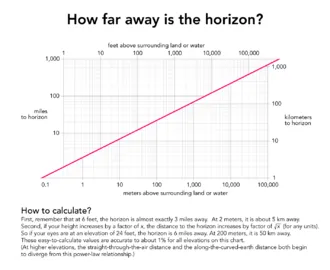
Из этого следует, что расстояние до видимого горизонта напрямую зависит от того, на какой высоте вы находитесь. И чем выше вы находитесь, тем дальше от вас линия. Некоторые примеры того, как высота точки наблюдения влияет на расстояние до горизонта:

человек на земле (при росте 1,75 м) – 4,7 км до горизонта;
с крыши восьмиэтажного здания на высоте 25 м – 17,9 км;
с горы высотой 2000 м – 159,8 км;
из самолета на высоте 10000 м – 357,3 км.

Интересный факт: В астрономии также существует понятие горизонта. Существует также понятие астрономии, но космический горизонт простирается на гораздо большие расстояния. А видимость ограничена самыми далекими звездами, которые люди могут увидеть с помощью приборов. И они находятся на расстоянии 13-14 миллиардов световых лет.

Если мы считаем горизонт всем пространством, которое атом может видеть вокруг себя, то видимость ограничена ближайшим объектом.

Какой длины горизонт?

При наблюдении за горизонтом атом обычно помещают в центр сферы. Различные лучи проходят через его глаза и касаются поверхности земли в определенных точках. Поэтому для наблюдателя видимый горизонт — это круг, образованный этими точками.

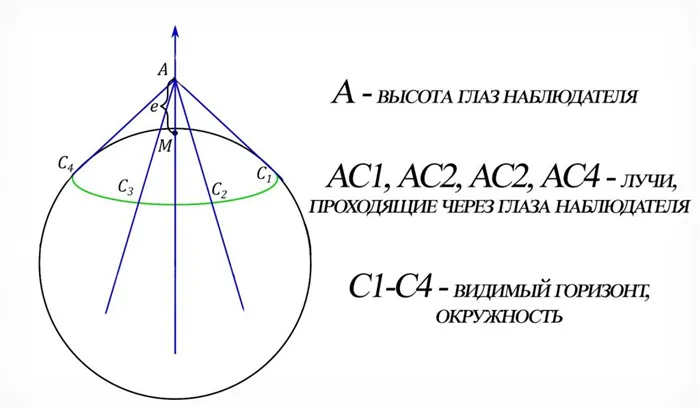
Если вы знаете расстояние до горизонта, вы также можете рассчитать его длину. Для этого используйте формулу длины окружности:

I = 2πr, где I — длина окружности, π — постоянная (3.14), а r — радиус окружности.

В нашем случае радиус соответствует расстоянию от горизонта. Поэтому для атома среднего размера, стоящего на земле, длина горизонта равна:

I = 2×3,14×4,7 = 29,5 км.

Аналогичным образом длина горизонта может быть определена и для других данных: наблюдателя, стоящего на крыше здания или на вершине горы и т.д.

Расстояние до горизонта

Если пренебречь эффектом атмосферной рефракции, расстояние до истинного горизонта от наблюдателя, находящегося у поверхности Земли, составляет около 2

где — часовая высота над уровнем моря, а p — радиус Земли.

Если d измеряется в километрах, а час — в метрах, то расстояние составляет

где константа 3,57 — единица км/м ½.

Если d измеряется в милях (statute miles, т.е. «сухопутные мили» 5 280 футов (1609 344 м)2 ), а час — в футах, то расстояние составляет

где константа 1,22 имеет единицу измерения мили / ½ фута.

В этом уравнении предполагается, что поверхность Земли идеально сферическая, где p составляет около 6371 км (3959 миль).

Примеры

Предположим, что атмосферная рефракция отсутствует, а Земля имеет сферическую форму с радиусом R = 6371 километр (3959 миль):

Для наблюдателя, стоящего на земле с час = 1,70 метра (5 футов 7 дюймов), горизонт находится на расстоянии 4,7 км (2,9 мили).
Для наблюдателя, стоящего на земле с час = 2 метра (6 футов 7 дюймов), горизонт находится на расстоянии 5 километров (3,1 мили).
Для наблюдателя, стоящего на холме или башне на высоте 30 метров (98 футов) над уровнем моря, горизонт находится на расстоянии 19,6 км (12,2 мили).
Для наблюдателя, стоящего на холме или башне на высоте 100 метров (330 футов) над уровнем моря, горизонт находится на расстоянии 36 километров (22 миль).
Для наблюдателя, стоящего на крыше Бурдж-Халифа, 828 метров (2717 футов) от земли и около 834 метра (2736 футов) над уровнем моря, горизонт находится на расстоянии 103 км (64 мили).
Для наблюдателя наверху гора Эверест (8 848 метров (29 029 футов) в высоту), горизонт находится на расстоянии 336 километров (209 миль).
Для U-2 пилот, летя на высоте 21 000 метров (69 000 футов), горизонт находится на расстоянии 521 километра (324 мили).

Другие планеты

Для планет земной группы и других твердых небесных тел с пренебрежимо малым влиянием атмосферы расстояние до горизонта для «типичного наблюдателя» меняется с квадратным корнем из радиуса планеты. Так, на Меркурии горизонт находится на 62% дальше от наблюдателя, чем на Земле, на Марсе — на 73%, на Луне — на 52%, на Мимасе — на 18% и так далее.

Вывод

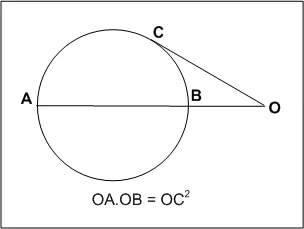
Геометрическая основа для вычисления расстояния до горизонта, теорема о вторичной касательной

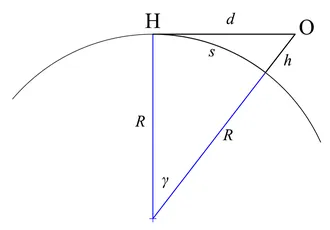
Геометрическое расстояние от горизонта, теорема Пифагора

Если предположить, что Земля представляет собой безликий шар (а не сплюснутый сфероид) без атмосферной рефракции, то легко рассчитать расстояние до горизонта. 6

O C 2 = O A × O B .

Сделайте следующие замены:

d = OC = расстояние до горизонта
D = AB = диаметр Земли
час = OB = высота наблюдателя над уровнем моря
Д + ч = OA = диаметр Земли плюс высота наблюдателя над уровнем моря,

с е, е и время измеряются в одних и тех же единицах. Сейчас формула выглядит следующим образом

d 2 = час ( D + час )

Прочие меры

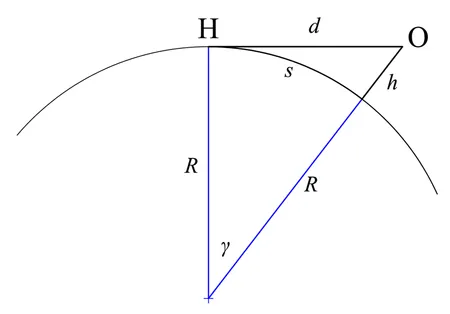
Расстояние дуги

Другое отношение — это расстояние по дуге s через изогнутую поверхность Земли до горизонта, которое содержит c в радианах,

Решение для s дает

Расстояние s также можно выразить через видимость d, как показано на втором рисунке справа,

Замена γ и перестановка дают

Расстояния d и s почти равны, когда высота объекта пренебрежимо мала по отношению к радиусу (т.е. время ≪ p ).

Зенитный угол

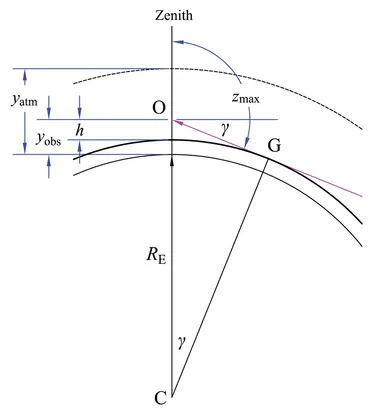
Максимальный зенитный угол для наблюдателя в однородной сферической атмосфере.

Когда наблюдатель находится на возвышенности, зенитный угол горизонта может быть больше 90°. Максимальный видимый зенитный угол возникает, когда луч касается поверхности Земли, как показано в треугольнике OCG на рисунке справа,

где времяэто высота наблюдателя над поверхностью, а c— угловой наклон горизонта. Это связано с зенитным углом горизонта. zиз:

Для неотрицательной высоты h, zвсегда ≥ 90°.

Объекты над горизонтом

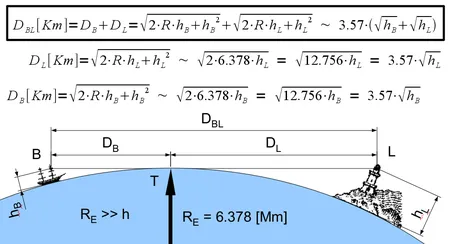
Чтобы рассчитать наибольшее расстояние, на котором наблюдатель может видеть вершину объекта над горизонтом, рассчитайте расстояние от горизонта для гипотетического наблюдателя на вершине объекта и прибавьте его к расстоянию реального наблюдателя от горизонта. Например, для наблюдателя ростом 1,70 м, стоящего на земле, горизонт находится на расстоянии 4,65 км. Для башни высотой 100 м расстояние до горизонта составляет 35,7 км. Таким образом, наблюдатель на пляже может увидеть вершину башни, если она находится на расстоянии не более 40,35 км. С другой стороны, если наблюдатель на лодке (время = 1,7 м) может видеть только верхушки деревьев на ближайшем побережье (время = 10 м), то деревья, вероятно, находятся на расстоянии около 16 км.

На рисунке справа верхушка маяка была бы видна наблюдателям в «вороньем гнезде» мачты судна, если бы

где D_BLв километрах и времени_Bи время_Lв метрах.

Вид на залив шириной 20 км на побережье Испании. Обратите внимание на изгиб земли, который скрывает фундаменты зданий на противоположном берегу.

Другой пример: наблюдатель, чьи глаза находятся на высоте двух метров над землей, смотрит в бинокль на далекое здание, которое, как он знает, имеет тридцать этажей по 3,5 метра каждый. Он считает, сколько этажей он может видеть, и обнаруживает, что их всего десять. Поэтому двадцать этажей или семьдесят метров здания скрыты от него из-за кривизны земли. Отсюда он может рассчитать расстояние до здания:

что составляет около 35 км.

Аналогичным образом он может рассчитать, какая часть удаленного объекта видна над горизонтом. Предположим, что глаз наблюдателя находится на высоте 10 метров над уровнем моря, и он наблюдает за кораблем на расстоянии 20 километров. Его горизонт:

Эффект атмосферной рефракции

Из-за атмосферной рефракции расстояние до видимого горизонта больше, чем расстояние, получаемое в результате простого геометрического расчета. Если поверхность земли (или воды) холоднее, чем воздух над ней, то вблизи поверхности образуется холодный плотный слой воздуха, в результате чего свет преломляется на пути вниз и, следовательно, в некоторой степени рассеивается у поверхности. И наоборот, когда земля теплее воздуха над ней, как это часто бывает в пустынях, возникают миражи. В качестве грубой компенсации рефракции геодезисты, измеряющие расстояния более 100 метров, вычитают 14% из рассчитанной ошибки кривизны и следят за тем, чтобы линия визирования находилась на расстоянии не менее 1,5 метров от земли, чтобы уменьшить случайные ошибки, вызванные рефракцией.

Если бы Земля была безвоздушным миром, как Луна, то приведенные выше расчеты были бы верны. Однако Земля имеет воздушную атмосферу, плотность и коэффициент преломления которой сильно варьируются в зависимости от температуры и давления. Это заставляет воздух в разной степени преломлять свет, что влияет на внешний вид горизонта. Обычно плотность воздуха непосредственно над поверхностью Земли больше, чем на больших высотах. В результате показатель преломления выше у поверхности, чем на больших высотах, так что свет, идущий горизонтально, преломляется примерно вниз. 7 Таким образом, фактическое расстояние до горизонта больше, чем расстояние, рассчитанное по геометрическим формулам. При нормальных атмосферных условиях разница составляет около 8 %. Это изменяет коэффициент с 3,57 в метрических формулах, использованных выше, до примерно 3,86. 2 Например, если наблюдатель стоит на берегу моря с глазами на высоте 1,70 м над уровнем моря, то приведенные простые геометрические формулы должны дать 4,7 км над горизонтом. В действительности, из-за атмосферной рефракции наблюдатель видит на 300 м дальше, что отодвигает реальный горизонт на 5 км от наблюдателя.

Эта поправка может быть, и часто применяется, как достаточно хорошее приближение, когда атмосферные условия близки к стандартным. В необычных условиях этот подход не работает. На преломление сильно влияют температурные градиенты, которые могут значительно меняться изо дня в день, особенно над водой. В экстремальных случаях, обычно весной, когда теплый воздух превышает холодную воду, преломление может привести к тому, что свет будет следовать за поверхностью Земли на протяжении сотен километров. Противоположные условия преобладают, например, в пустынях, где поверхность очень теплая, так что теплый воздух с низкой плотностью находится ниже более холодного воздуха. Из-за этого свет преломляется вверх, что приводит к появлению миражей, которые в некотором смысле делают понятие горизонта бессмысленным. Поэтому рассчитанные значения для эффектов преломления в необычных условиях являются приближенными. 2 Тем не менее, были предприняты попытки рассчитать их более точно, чем с помощью простой аппроксимации, описанной выше.

За пределами видимого диапазона длин волн преломление происходит по-другому. Для радаров (например, для длин волн от 300 до 3 мм, т.е. частот от 1 до 100 ГГц) радиус Земли можно умножить на 4/3 для получения фактического радиуса, что дает коэффициент 4,12 в метрической формуле, т.е. горизонт радара на 15% выше геометрического горизонта или на 7% выше оптического горизонта. Коэффициент 4/3 не является точным, поскольку в оптическом случае преломление зависит от атмосферных условий.

С глаз долой

Из-за конечной скорости света наблюдатель видит небесные объекты такими, какими они были в более или менее отдаленном прошлом. За горизонтом частиц находятся галактики, которые не наблюдаются ни на одном из этапов их прошлой эволюции. Это означает, что их глобальные линии в пространстве-времени нигде не пересекают поверхность, по которой распространяется свет и достигает наблюдателя с момента рождения Вселенной (так называемый ретроградный световой конус). В пределах горизонта частиц находятся галактики, космические линии которых пересекали эту поверхность в прошлом. Эти галактики являются той частью Вселенной, которая в принципе наблюдаема в настоящее время.

Конус ретроградного света любого наблюдателя в расширяющейся Вселенной после Большого взрыва сходится к этой начальной сингулярности и охватывает конечный объем. Из этого, в свою очередь, следует, что наблюдатель может видеть только конечную часть своего мира. Поэтому мы не знаем, как выглядит Вселенная за пределами нынешнего горизонта частиц. Некоторые теории о ранней Вселенной говорят, что далеко за этим горизонтом все выглядит не так, как мы видим. Эта позиция вполне научна, поскольку вытекает из вполне разумных расчетов, но она не может быть опровергнута или подтверждена имеющимися на сегодняшний день астрономическими наблюдениями. Если пространство продолжит расширяться ускоренными темпами, это невозможно будет проверить даже в отдаленном будущем.

В статичной Вселенной с фиксированным началом координат радиус горизонта частицы равен произведению ее возраста на скорость света. В нашей Вселенной он гораздо больше, потому что расширяющееся пространство притягивает световые кванты. Определение этого радиуса требует знания всей динамики Вселенной, включая инфляционную фазу, которой наука пока не располагает. Современные данные свидетельствуют о том, что масштабный фактор Вселенной во время инфляции увеличился по меньшей мере в 1027 раз, но эта оценка может быть сильно занижена (стандартная космологическая модель вообще не описывает инфляционную фазу и измеряет возраст Вселенной от ее конца). В мире Эйнштейна-де Ситтера радиус горизонта частиц равен удвоенному радиусу сферы Хаббла, который, в свою очередь, в полтора раза больше произведения возраста этого мира и скорости света. Легко подсчитать, что, согласно этой модели, нынешний радиус горизонта частиц (и, следовательно, радиус области пространства, наблюдаемой с Земли) составляет около 41 миллиарда световых лет или 13 гигапарсек. Поскольку Вселенная начала ускорять свое расширение в период доминирования темной энергии, радиус горизонта частиц должен быть несколько больше. Однако если мы учтем темную энергию, то получим довольно точное значение в 14 гигапарсек.

Эффект атмосферной рефракции править

Из-за атмосферной рефракции расстояние до видимого горизонта больше, чем расстояние, которое получается в результате простого геометрического расчета. Когда поверхность Земли (или вода) холоднее, чем воздух над ней, у поверхности образуется холодный плотный слой воздуха, в результате чего свет преломляется на пути вниз и, следовательно, в некоторой степени рассеивается у поверхности. И наоборот, когда земля теплее воздуха над ней, как это часто бывает в пустынях, возникают миражи. В качестве грубой компенсации рефракции геодезисты, измеряющие расстояния более 100 метров, вычитают 14% из рассчитанной ошибки кривизны и следят за тем, чтобы линия визирования находилась на расстоянии не менее 1,5 метров от земли, чтобы уменьшить случайные ошибки, вызванные рефракцией.

Если бы Земля была безвоздушным миром, как Луна, то приведенные выше расчеты были бы верны. Однако Земля имеет воздушную атмосферу, плотность и коэффициент преломления которой сильно варьируются в зависимости от температуры и давления. Это заставляет воздух в разной степени преломлять свет, что влияет на внешний вид горизонта. Как правило, плотность воздуха непосредственно над земной поверхностью больше, чем на больших высотах. В результате, его коэффициент преломления выше у поверхности, чем на больших высотах, поэтому свет, движущийся горизонтально, преломляется вниз. 7 Таким образом, фактическое расстояние до горизонта больше, чем расстояние, рассчитанное по геометрическим формулам. При нормальных атмосферных условиях разница составляет около 8 %. Это меняет коэффициент 3,57 в метрических формулах, использованных выше, примерно на 3,86. 2 Например, если наблюдатель стоит на берегу моря с глазами на высоте 1,70 м над уровнем моря, горизонт должен находиться на расстоянии 4,7 км в соответствии с простыми геометрическими формулами, приведенными выше. В действительности, из-за атмосферной рефракции наблюдатель видит на 300 м дальше, что отодвигает реальный горизонт на 5 км от наблюдателя.

Эта поправка может быть, и часто применяется, как достаточно хорошее приближение, когда атмосферные условия приблизительно нормальные. В необычных условиях этот подход не работает. На преломление сильно влияют температурные градиенты, которые могут значительно меняться изо дня в день, особенно над водой. В экстремальных случаях, обычно весной, когда теплый воздух заливает холодную воду, преломление может привести к тому, что свет будет следовать за поверхностью Земли на протяжении сотен километров. Противоположные условия преобладают, например, в пустынях, где поверхность очень горячая, так что теплый воздух с низкой плотностью находится ниже более холодного воздуха. В результате свет преломляется вверх, что приводит к появлению миражей, которые в некотором смысле делают понятие горизонта бессмысленным. Поэтому рассчитанные значения для эффектов преломления в необычных условиях являются приближенными. 2 Тем не менее, были предприняты попытки рассчитать их более точно, чем с помощью простой аппроксимации, описанной выше.

Кривизна горизонта редактировать

Кривизна горизонта хорошо видна на этой фотографии 2008 года, сделанной космическим кораблем Space Shuttle с высоты 226 км.

С точки, расположенной над поверхностью Земли, горизонт кажется слегка изогнутым; это дуга окружности. Следующая формула выражает основную геометрическую связь между этой оптической кривизной, высотой и радиусом Земли: k h R

Кривизна является обратной величиной радиуса кривизны в радианах: кривизна 1,0 соответствует окружности с угловым радиусом 57,3°, что соответствует высоте около 2640 км над поверхностью Земли. На высоте 10 км (33 000 футов), на которой находится типичный самолет, математическая кривизна горизонта составляет около 0,056, что соответствует кривизне радиуса круга радиусом 10 м (16,5 футов), если смотреть на него с высоты 56 см (16,5 дюйма) непосредственно над центром круга. Однако видимая кривизна меньше, чем кривизна, вызванная преломлением света через атмосферу и закрытием горизонта высокими слоями облаков, которые уменьшают высоту над видимой поверхностью.

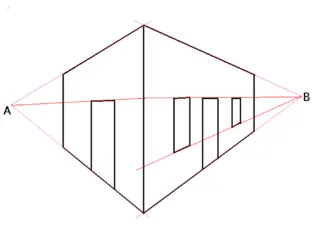
Точки схода править

Две точки на горизонте находятся на пересечении линий, которые продолжают отрезки, представляющие края здания на переднем плане. Линия горизонта здесь совпадает с линией в верхней части дверей и окон.

Горизонт является неотъемлемой характеристикой картинной плоскости в науке о графической перспективе. Если предположить, что плоскость изображения перпендикулярна земле, а P — перпендикулярная проекция точки глаза O на плоскость изображения, то горизонт определяется как горизонтальная линия, проходящая через P. Точка P — это точка схождения линий, перпендикулярных плоскости изображения. Если S — другая точка на горизонте, то точка схода всех прямых параллельна О. Но Брук Тейлор (1719) указал, что плоскость горизонта, определяемая О и горизонтом, подобна любой другой плоскости:

Термин «горизонтальная линия», например, имеет тенденцию ограничивать представления ученика плоскостью горизонта и заставлять его думать, что эта плоскость пользуется особыми привилегиями, которые делают описание фигур на ней более простым и удобным, чем описание фигур на любой другой плоскости. Но в этой книге я не делаю различий между горизонтальной и любой другой плоскостью. 9 10

Особая геометрия перспективы, где параллельные линии сходятся на определенном расстоянии, привела к развитию проективной геометрии, где существует точка на бесконечности, в которой сходятся параллельные линии. В своей книге «Геометрия искусства» (2007) Кирсти Андерсен описывает развитие перспективного рисунка и науки примерно до 1800 года и утверждает, что точки схода не обязательно должны находиться на горизонте. В главе под названием «Горизонт» Джон Стиллвелл объясняет, как проективная геометрия привела к геометрии случайностей — современному абстрактному исследованию пересечения линий. Стилвелл также попытался разобраться с основами математики; в статье «Каковы законы алгебры?» Алгебра точек», первоначально данная Карлом фон Штаудтом при выводе аксиом поля, была деконструирована в двадцатом веке и открыла широкий спектр математических возможностей. Стиллвелл объясняет

Это открытие, сделанное более 100 лет назад, кажется, способно перевернуть математику с ног на голову, даже если математическое сообщество еще не полностью приняло его. Она не только бросает вызов тенденции превращать геометрию в алгебру, но и предполагает, что и геометрия, и алгебра имеют более простую основу, чем считалось ранее 11