Звук — это вибрация среды, воспринимаемая органами слуха. Отрасль физики, изучающая звуковые явления, называется акустикой.
Термины
- Скорость волны – абсолютный показатель скорости, при которой проходит фаза любого частотного компонента волны.
- Частота – соотношение числа периодического явления к временному промежутку: f = n/t.
Если вы посмотрите на видимый свет, то сможете представить его как электромагнитную волну. Она представлена электрическими и магнитными полями, которые смещаются в среде. Частота определяется как цвет: 4 × 10 14 Гц (красный), 8 × 10 14 Гц (фиолетовый) и все, что между ними. Длина волны обратно пропорциональна частоте: чем выше частота, тем короче длина.
Свойства волн
Волны характеризуются своими свойствами. Амплитуда равна половине расстояния между пиком и впадиной. Вы также можете увидеть длину волны — пространственный период (от пика до пика), обозначенный буквой λ.
Частота — количество циклов, пройденных за определенный промежуток времени. С точки зрения формул:
Красная волна — это низкочастотная синусоидальная волна, поэтому циклы почти не повторяются. Фиолетовая волна, с другой стороны, имеет высокую частоту. Обратите внимание, что время увеличивается в горизонтальном направлении.
f = 1/T (T — период колебаний).
Частота и длина волны также могут быть связаны со «скоростью» волны. Мы получаем:
v = fλ (v — скорость волны или фазовая скорость, с которой фаза волны распространяется в пространстве).
Существует также групповая скорость волны, т.е. скорость, с которой вся амплитудная форма волны (волновая модуляция или огибающая волны) распространяется в пространстве.
За ней следует волна с групповой скоростью (положительной) и фазовой скоростью (отрицательной), движущаяся в разных направлениях
Основная формула для определения фазовой скорости (монохроматической) волны в одномерном пространстве или фазовой скорости вдоль волнового вектора для волны в более высокоразмерном пространстве:
что является прямым следствием того, что фаза плоской волны в однородной среде равна
ή
Конкретная зависимость между ω и k, известная как закон дисперсии для конкретного типа волны, обычно выводится из дифференциального уравнения, описывающего данный тип волны, путем рассмотрения монохроматической (обычно плоской) волны 1
Если фазовая скорость для определенного типа волны не зависит от частоты или волнового числа (и направления волнового вектора), то групповая скорость совпадает с ней.
Фазовая скорость электромагнитной волны
В вакууме для электромагнитной волны любой частоты (по крайней мере, в изученных диапазонах частот и интенсивности) фазовая скорость, измеренная в направлении волнового вектора, всегда равна одной и той же величине — скорости света в вакууме, универсальной постоянной.
В среде закон рассеяния электромагнитных волн довольно сложен (см. рассеяние света), и фазовая скорость может значительно меняться.
Для волнового уравнения
= C^2 \frac<\partial^2 f><\partial x^2>» width=»» height=»» />
имеет фазовую скорость C (причем C здесь — постоянный коэффициент; скорость света равна этому коэффициенту в волновом уравнении для электромагнитных волн).
Этот результат получается путем прямой подстановки монохроматической волны в форму этого уравнения.
Этот результат справедлив не только для волнового уравнения в одномерном пространстве (мы использовали его выше только для краткости; для любого числа координатных производных в правой части все остается полностью аналогичным).
Для уравнения Клейна — Гордона
= C^2 \frac<\partial^2 f><\partial x^2>+ C^4 m^2 f,» width=»» height=»» />
который отличается только последним членом, дает путем аналогичной замены
(Это выражение для ненулевого вещественного m всегда больше C и может быть произвольно большим, если k → 0.
Фазовая скорость как вектор
В некотором смысле, фазовая скорость не является вектором. Под этим подразумевают тот факт, что фазовые скорости в различных направлениях (например, в направлениях координатных осей), определенные, как описано выше, не являются ни координатами, ни проекциями 2 какого-либо вектора 3, включая, конечно, непроекции или координаты вектора, совпадающего с волновым вектором, абсолютное значение которого равно фазовой скорости в этом направлении.
Однако это не мешает ввести, чисто формально, вектор фазовой скорости, который, по определению, совпадает с волновым вектором и абсолютное значение которого равно фазовой скорости в этом направлении, по желанию. Вопрос о том, правильно ли называть такой вектор вектором фазовой скорости, является чисто терминологическим (условным); дело лишь в том, что его проекции на координатные оси или его компоненты вдоль этих осей не соответствуют фазовой скорости вдоль этих направлений согласно определению фазовой скорости по направлению, данному в начале этого очерка (и вообще любому разумному определению, кроме чисто формального, описанного в этом параграфе).
В частности, для случая плоской гармонической волны фазовая скорость вдоль волнового вектора может быть выражена следующим образом:
Где k — волновое число, а ω — угловая частота.
Таким образом, фазовая скорость вдоль направления, отклоненного от волнового вектора на один угол, составляет.
>» width=»» height=»» />
Непонимание этого факта часто служит причиной недоразумений и ошибок. Например, из приведенного выше ясно, что фазовая скорость может быть больше скорости света (это вытекает прямо из только что приведенной формулы, учитывая что
Может ли фазовая скорость превосходить скорость света
Фазовая скорость может и часто превышает скорость света в вакууме. Это никоим образом не противоречит известному принципу максимальной скорости света, необходимость которого вытекает из того, что соблюдается как принцип причинности (чтобы не было причинных парадоксов), так и принцип относительности (инвариантность Лоренца).
Дело в том, что эти принципы ограничивают лишь скорость, с которой эти физические объекты могут передавать информацию. А фазовая скорость 5 не относится к скорости этих объектов. Чисто монохроматическая (синусоидальная) волна пространственно и временно бесконечна и не может быть изменена каким-либо образом для передачи информации (если мы модулируем волну, она уже не монохроматическая, а скорость распространения модуляции не соответствует фазовой скорости, которая обычно соответствует групповой скорости для почти монохроматических волн).
Фазовая скорость по направлению, не совпадающему с волновым вектором
Поскольку фазовая скорость, измеренная вдоль любого направления, не совпадающего с волновым вектором и направлением распространения волны, не является скоростью «физического объекта», т.е. объекта, состояние которого в последующие моменты времени причинно обусловлено его состоянием в предыдущие моменты времени, а лишь характеризует состояние колебательного поля в искусственно выбранных точках, то часто (т.е. при достаточно большом угле с волновым вектором) скорость
В частности, фазовая скорость света (или электромагнитной волны в целом) в вакууме, измеренная вдоль любого направления, не совпадающего с его волновым вектором, всегда больше скорости света.
Однако она не ограничивается фазовой скоростью вдоль любого направления. Скорость света может быть даже превышена фазовой скоростью, измеренной вдоль волнового вектора.
Фазовая скорость для квантовой частицы
Фазовая скорость квантовой волны, соответствующей любой частице с массой (т.е. частице с массой больше нуля), всегда больше скорости света. Это легко читается из формул и, в то время как E всегда больше p для массивных частиц из-за массы (энергии покоя).
Однако в квантовой физике — по крайней мере, в ее современной формулировке — эта фазовая скорость в принципе не может наблюдаться непосредственно (поскольку фаза в общем случае не наблюдаема). Наблюдаемой является только групповая скорость, которая является квантовым аналогом обычной скорости классической частицы.
Фазовая скорость для уравнения Клейна — Гордона
Но дифференциальные уравнения, описывающие квантовые частицы, в принципе могут быть применены и к другим физическим системам (например, к довольно простым механическим моделям). В этом случае фазовая скорость легко наблюдаема.
Но и здесь фазовую скорость можно сделать произвольно большой (при условии, что мы выбираем достаточно малый k), и в принципе нетрудно сделать ее больше скорости света.
Этот кажущийся парадоксальным результат объясняется тем, что «распространение» такой волны является иллюзией в том смысле, что между различными частями волны не существует причинно-следственной связи (состояние волны, которая пошла вправо, не определяется тем, что было слева). В этом смысле состояние сравнимо с состоянием кролика, движущегося быстрее света, и т.д.
7. Интерференция упругих волн
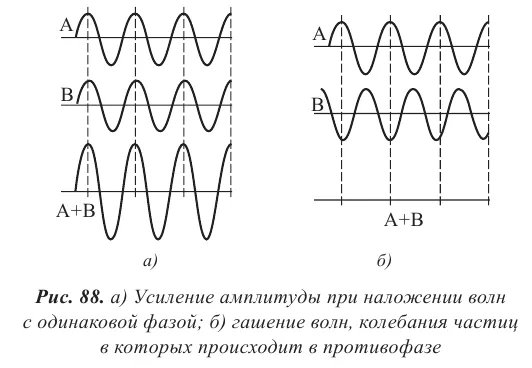
Чтобы рассмотреть интерференцию волн, мы должны ввести понятие когерентности. Согласованный ход различных колебательных или волновых процессов в пространстве и времени связан с понятием когерентности. Волны считаются когерентными, если их разность фаз остается постоянной во времени. Когда две или более когерентные волны накладываются в разных точках пространства, происходит усиление или ослабление результирующей волны, в зависимости от соотношения фаз этих волн. Это явление называется интерференцией волн и заключается в том, что колебания усиливаются друг относительно друга в одних точках и ослабевают в других.
Рассмотрим суперпозицию двух когерентных сферических волн, возбуждаемых точечными источниками $S_1$ и $S_2$ и колеблющихся с одинаковой амплитудой, частотой, нулевой начальной фазой и постоянной разностью фаз. Запишем уравнения колебаний:
Где $r_1$ и $r_2$ — расстояния источников волн от рассматриваемой точки.
Амплитуда результирующей волны равна (сложение уравновешенных колебаний).
Поскольку разность начальных фаз равна $(ϕ_1-ϕ_2)=(r_2-r_1)=Δ=const$, результат суперпозиции двух волн в разных точках зависит от величины $Δ=r_2-r_1$, которая называется разностью пути волны.
В тех точках, где состояние.
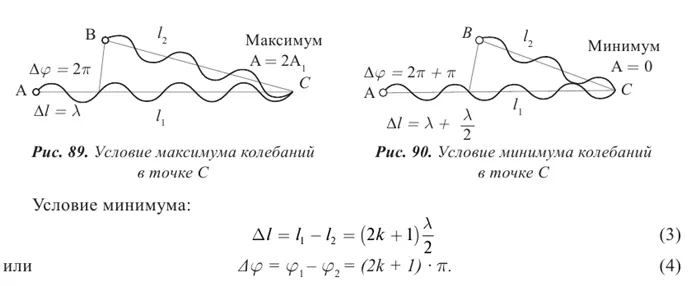
Поскольку квадрат амплитуды колебаний пропорционален интенсивности волны, результат
То есть происходит амплификация (увеличение амплитуды) результирующей волны или интерференционного максимума.
2) В точках, где условие
То есть наблюдается снижение интенсивности (уменьшение амплитуды) результирующей волны или интерференционный минимум.
Таким образом, суперпозиция двух когерентных волн в среде вызывает колебания с разными амплитудами в разных точках среды, и в каждой точке среды существует либо максимальная амплитуда, либо минимальная амплитуда, либо промежуточное значение — в зависимости от расстояния точки от когерентных источников. Интерференция света приводит к перераспределению энергии волны между соседними областями, хотя в среднем энергия остается одинаковой для больших областей.
8. Стоячие волны
Рассмотрим интерференцию стоячих волн. Стоячие волны — это волны, возникающие в результате суперпозиции двух волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Напишем уравнение для двух плоских волн, распространяющихся вдоль оси x в противоположных направлениях
Если сложить оба уравнения и преобразовать результат с помощью уравнения косинусной суммы, то получим уравнение стоячей волны

Из этого уравнения видно, что в каждой точке стоячей волны колебания происходят с той же частотой, что и противоточные волны, а амплитуда зависит от координаты x
Точки, в которых амплитуда колебаний достигает максимального значения и координаты которых удовлетворяют следующему условию

где m = 0, 1, 1, 2, … называются муфтами стоячей волны.
Точки, в которых амплитуда колебаний достигает нуля и координаты которых удовлетворяют условию
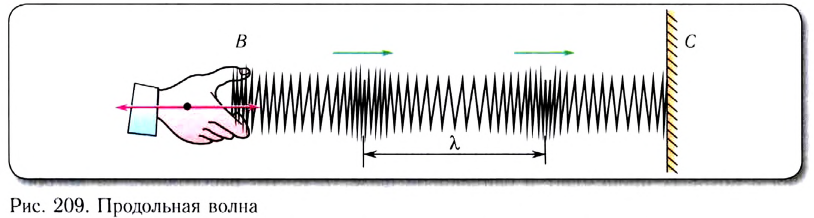
где m = 0, 1, 2, … являются узлами стоячей волны.
Стоячие волны
Уравнение стоячей волны При отражении от более плотной среды волна меняет свое направление на противоположное, а затем свою фазу на

Мы получим уравнение стоячей волны, сложив уравнения распространяющихся волн:
Заменив количество волн на значение
Координаты штриховых и узловых точек определяются условиями большего и меньшего значений амплитуды. На сайте
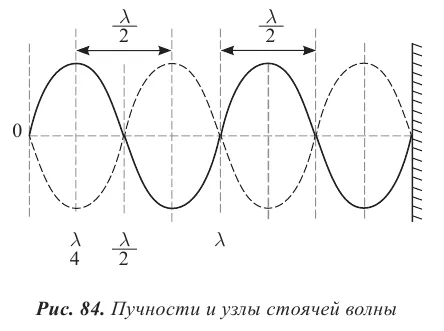
На сайте
Расстояния между двумя соседними точками пересечения или двумя соседними узлами равны:
В стоячей волне нет потока энергии. Колебательная энергия, содержащаяся в одной части струны между двумя соседними узлами, не передается другим частям струны. В каждом из этих участков кинетическая энергия дважды за один период преобразуется в динамическую и обратно, как в обычной колебательной системе. Отсутствие передачи энергии является характерной особенностью стоячей волны.
Пример:
Уравнение бегущей волны показано на рисунке (рис. 85):
А. Найдите уравнение стоячей волны как суммы падающей и отраженной волн.
В. Запишите выражение, полученное при замене числа волн и циклической частоты на длину волны и период.
С. Определите положение узлов и стержней.
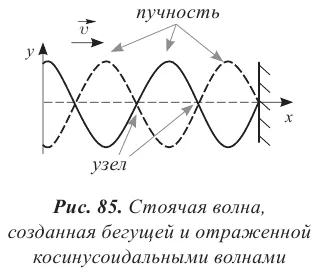
Дано:
Решение: A. Уравнение стоячей волны определяется путем сложения уравнений бегущих волн:
В.
С. На сайте
С. Расстояние до узловых точек определяем по условию.

Реакция:
Интерференция волн
Когда несколько источников возбуждают механические волны в среде, они распространяются независимо друг от друга. Все точки среды участвуют в колебаниях, вызванных каждой волной в отдельности. Наложение волн, приводящее к устойчивой картине чередующихся максимальных и минимальных колебаний частиц среды, называется интерференцией.
Интерферировать могут только те волны, которые имеют одинаковую частоту и постоянный сдвиг фаз. Такие волны называются когерентными и генерируются источниками, колеблющимися с одинаковой частотой и с постоянным сдвигом фаз.
Интерференция — это взаимное увеличение или уменьшение результирующей амплитуды двух или более когерентных волн при их наложении друг на друга.
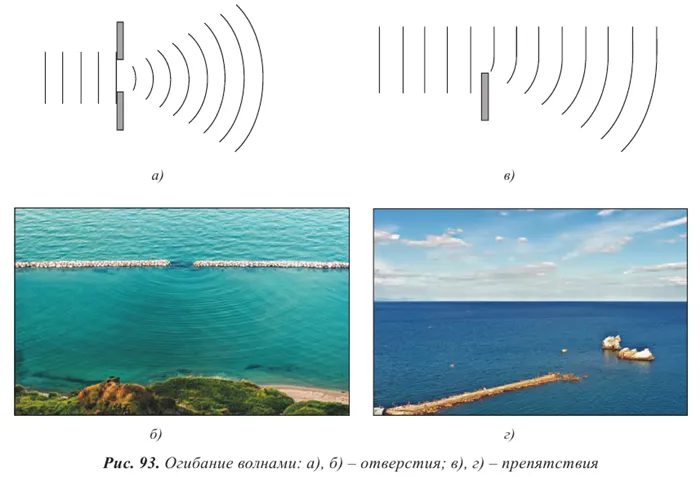
Помехи могут быть или не быть постоянными. Только когерентные волны могут создавать устойчивую интерференционную картину, например, две сферические волны на поверхности воды, исходящие от двух когерентных точечных источников (рис. 87).
Помните. Волны называются когерентными, если их источники колеблются на одной и той же частоте с постоянным сдвигом фаз.

Условие максимума и минимума при интерференции двух волн
Амплитуда наложенных колебаний определяется в соответствии с принципом суперпозиции (рис. 88). Если пики когерентных волн перекрываются в какой-то точке среды, колебания усиливаются, и амплитуда принимает значение, соответствующее сумме амплитуд. Если пик одной волны пересекается со впадиной другой волны, а амплитуды отдельных волн равны, то эта точка в пространстве не колеблется. Если амплитуды различны, то колебания в этой точке происходят с амплитудой, соответствующей разности между амплитудами распространяющихся волн.
Распространение колебаний в упругих средах. Продольные и поперечные волны
Опыт показывает, что вибрации, возникающие в одной точке упругой среды, с течением времени передаются другим точкам среды. В качестве примера достаточно вспомнить, что пульс измеряется на запястье, хотя сердце находится в груди. Эти явления связаны с распространением механических волн.
Механическая волна — это процесс распространения колебаний в упругой среде с передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме. Источником механических волн является вибрирующее тело. Если источник колеблется в виде синусоиды, то волна в упругой среде также будет синусоидой. Вибрации, инициированные в точке упругой среды, распространяются через среду с определенной скоростью, которая зависит от плотности и упругих свойств среды.
Следует подчеркнуть, что при распространении волны не происходит переноса вещества, т.е. частицы колеблются вблизи положения равновесия. Среднее смещение частиц за длительный период времени равно нулю. Давайте теперь рассмотрим наиболее важные характеристики волны.
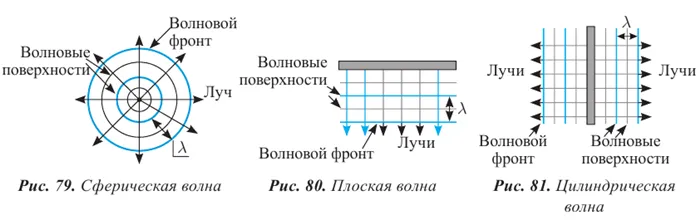
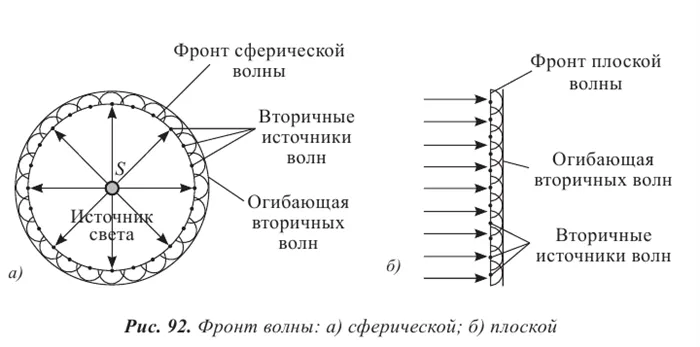
Волновой фронт — это воображаемая поверхность, которой волновое возмущение достигает в определенный момент времени.
Линия, проведенная перпендикулярно фронту волны в направлении распространения волны, называется радиусом. Радиус указывает направление распространения волны.
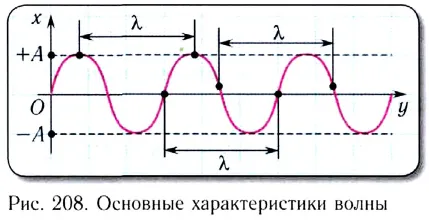
Основные характеристики волны следующие (Рисунок 208):
- амплитуда (A) — модуль максимального смещения точек среды из положений равновесия при колебаниях;
- период (T) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны);
- частота
- скорость
- длина волны
Рассмотрим колебания источника волны, происходящие с циклической частотой и амплитудой А:
и амплитудой А: где x(t) — смещение источника от положения равновесия.
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией где k — волновое число
где k — волновое число фаза волны.
фаза волны.
Выражение x(t, r) — это уравнение плоской волны, распространяющейся в направлении радиус-вектора.
Бегущую волну можно наблюдать с помощью следующего эксперимента: Если один конец упругой струны, лежащей на гладком горизонтальном столе, неподвижен, а другой конец заставить колебаться в направлении, перпендикулярном струне, осторожно потянув за него рукой, то вдоль него пойдет волна, описываемая уравнением плоской волны.
Для того чтобы сгенерировать F
Здесь ⋅
Эту концепцию можно понять, если представить часы как стрелку, которая вращается с постоянной скоростью и сбрасывается каждые T
Концепция фазы наиболее полезна, когда начало отсчета t 0
Из приведенной выше формулы следует, что фаза — это угол в радианах между 0 и 2 π
Фаза, выраженная в градусах (от 0° до 360° или о т-180° до + 180°), определяется таким же образом, с той разницей, что вместо «2π» используется «360°».
Последствия
Согласно одному из приведенных выше определений, фаза ϕ ( t )
Фаза равна нулю в начале каждого периода, т.е.
ϕ ( t 0 + k T ) = 0
Кроме того, для любого выбора начала координат t 0
Фактически, любой периодический сигнал F
F ( t ) = A sh ( ϕ ( t ) )
где w
Добавление и сравнение фаз
Поскольку фазы являются углами, полные вращения обычно игнорируются при выполнении арифметических операций. То есть, сумма и разность двух фаз (в градусах) рассчитываются по следующим формулам
соответственно. Например, сумма фазовых углов 190° + 200° равна 30° (190 + 200 = 390, минус один полный оборот), а вычитание 50° из 30° дает фазу 340° (30 — 50 = -20, плюс один полный оборот).
Аналогичные формулы применимы к радиусам, где 2 p
Сдвиг фазы
Иллюстрация фазового сдвига. На горизонтальной оси угол (фаза) увеличивается со временем.
Общее определение
Разница φ ( t ) = ϕ грамм ( t ) — ϕ F ( t )
По аналогии с часами, каждый сигнал представлен стрелкой тех же часов, вращающейся с постоянной, но, возможно, разной скоростью. Разность фаз — это угол между двумя стрелками, измеряемый по часовой стрелке.
Разность фаз особенно важна, когда два сигнала складываются в результате физического процесса, например, две периодические звуковые волны, излучаемые двумя источниками и улавливаемые микрофоном. Обычно это происходит в линейной системе, когда действует принцип суперпозиции.
Для аргументов t
Для синусоид
Для синусоидальных сигналов, если разность фаз φ ( t )
Если разность фаз φ ( t )
Если частоты разные, то разность фаз φ ( t )
Для смещенных сигналов
Разность фаз особенно важна при сравнении периодического сигнала. F
В этом случае сдвиг фазы — это просто сдвиг аргумента t
Если F
Таким образом, если два периодических сигнала имеют одинаковую частоту, они всегда находятся в фазе или всегда вне фазы. Конечно, существует много причин для такой ситуации. Например, два сигнала могут представлять собой периодическую звуковую волну, записанную двумя микрофонами в разных местах. Но это могут быть и периодические звуковые волны, генерируемые двумя отдельными громкоговорителями из одного и того же электрического сигнала и улавливаемые одним микрофоном. Это может быть радиосигнал, поступающий по прямой линии на приемную антенну, и его копия, отраженная от большого здания поблизости.








