Здесь ⋅
обозначает дробную часть действительного числа, опуская целую часть; то есть, X = X — ⌊ X ⌋. ; и t 0 — это любое «начальное» значение аргумента, которое считается началом цикла.
Фаза колебаний – кратко что это и в чем измеряется, определение, формула, единица измерения в физике
Определение Начальная фаза колебания — это параметр, который вместе с амплитудой колебания определяет начальное состояние колебательной системы. Значение начальной фазы задается при начальных условиях, т.е. $t=0$ c. Рассмотрим гармоническое колебание с заданным параметром $\xi$. Гармонические колебания описываются уравнением:
Где $A=<\xi>_$ — амплитуда колебаний; $.<\omega>_0$ — циклическая (круговая) частота колебаний. Параметр $\xi $ находится в диапазоне $-A\le \xi \le 3500A.
Параметры гармонического колебания
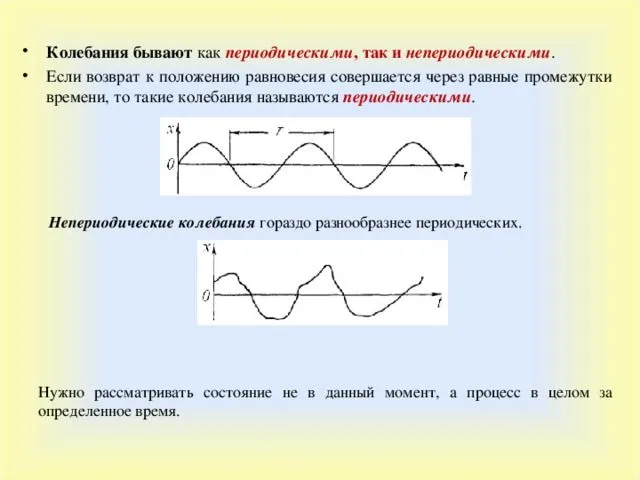
Каждый колебательный процесс — это колебание параметра вокруг среднего значения. Колебания могут быть периодическими (маятник) или непериодическими (флаг на ветру). График колебательного процесса представляет среднее значение в виде горизонтальной линии, а значение колебательного параметра — в виде кривой, которая постоянно возвращается к среднему значению. При непериодическом колебании доходность будет хаотичной, тогда как при периодическом колебании она будет находиться строго в одном и том же временном интервале. Этот интервал называется периодом колебаний $T$.
Читайте также: Выбор и подключение фотоэлектрического реле для уличного освещения.
Рисунок 1. Как выбрать лампу для уличного освещения?
Простейшее периодическое колебание — это колебание, которое следует закону циклических функций (синус или косинус). Она называется гармоничной. Поскольку в высшей математике доказано, что каждое колебание (включая непериодические) может быть представлено в виде бесконечной суммы гармонических колебаний, они рассматриваются в первую очередь. И по определению, каждое гармоническое колебание может быть представлено в виде функции:
A=A_0sin \Bigg (<2\pi\over T>t +\varphi_0 \Bigg ),$
- $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
- $T$ — период колебаний;
- $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
- $\varphi_0$ — начальная фаза колебаний.
Коэффициент $<2\pi\over T>=\омега$ в свободной переменной $t$ называется угловой частотой. Его физический смысл заключается в том, что это угол, через который проходит гармоническая функция за единицу времени. Значение выражения $<2\pi\over T>t +\varphi_0=\varphi$, который является аргументом синусоидальной функции, называется полной фазой колебания.
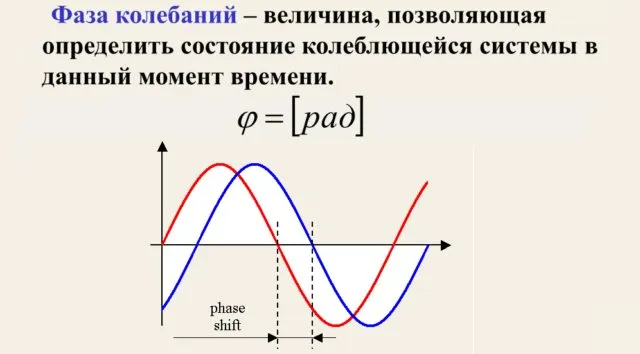
Рисунок 2. Фаза колебания.

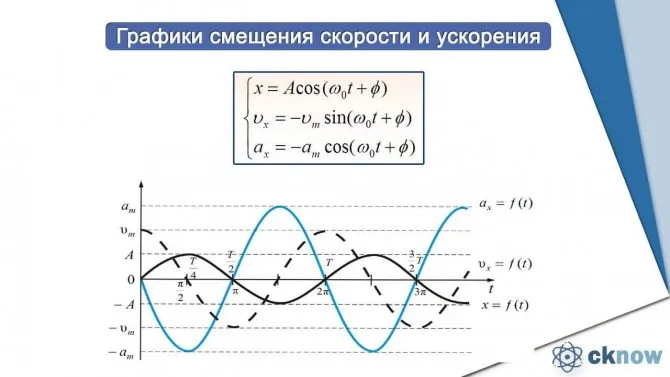


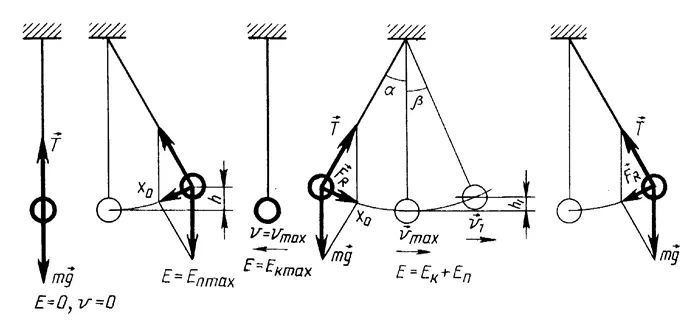

Вынужденные колебания. Резонанс
Вынужденное колебание не затухает. Поэтому необходимо компенсировать потерю энергии в каждом периоде колебаний. Это достигается путем приложения периодически изменяющейся силы к вибрирующему телу. Вынужденная вибрация происходит с частотой, которая соответствует частоте изменения внешней силы.
Амплитуда вынужденной механической вибрации будет больше, если частота вынуждающей силы равна частоте колебательной системы. Это явление называется резонансом.
Например, если проволоку периодически тянуть со скоростью ее собственных колебаний, можно наблюдать увеличение амплитуды ее колебаний.
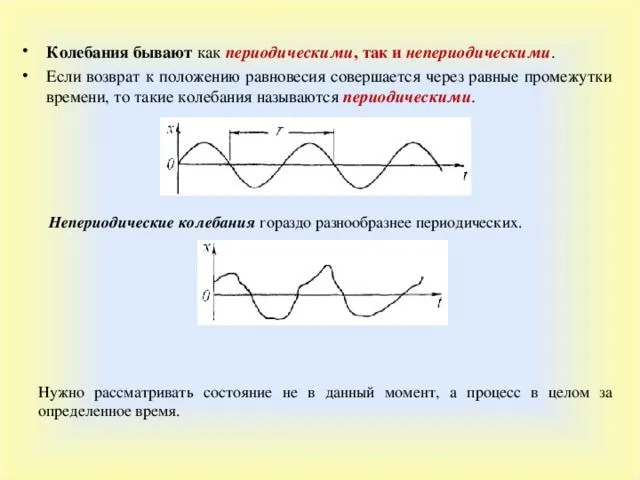
Параметры гармонического колебания
Каждый колебательный процесс — это колебание параметра вокруг среднего значения. Колебания могут быть периодическими (маятник) или непериодическими (флаг на ветру). График колебательного процесса представляет среднее значение в виде горизонтальной линии, а значение колебательного параметра — в виде кривой, которая постоянно возвращается к среднему значению. При непериодическом колебании доходность будет хаотичной, тогда как при периодическом колебании она будет находиться строго в одном и том же временном интервале. Этот интервал называется периодом колебаний $T$.
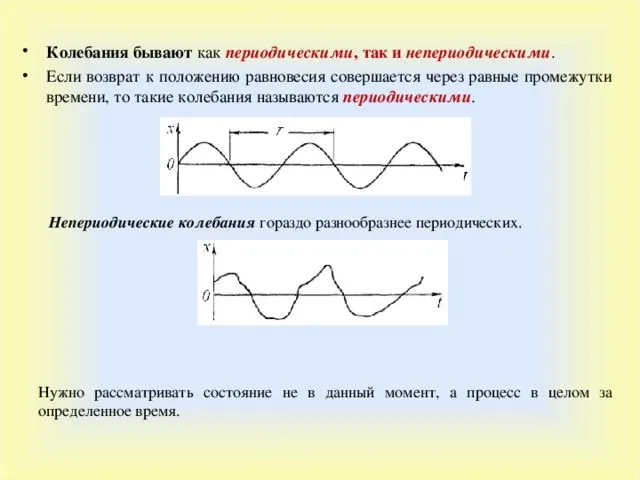
Простейшее периодическое колебание — это колебание, которое следует закону циклических функций (синус или косинус). Она называется гармоничной. Поскольку в высшей математике доказано, что каждое колебание (включая непериодические) может быть представлено в виде бесконечной суммы гармонических колебаний, они рассматриваются в первую очередь. И по определению, каждое гармоническое колебание может быть представлено в виде функции:
A=A_0sin \Bigg (<2\pi\over T>t +\varphi_0 \Bigg ),$
- $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
- $T$ — период колебаний;
- $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
- $\varphi_0$ — начальная фаза колебаний.
Коэффициент $<2\pi\over T>=\омега$ в свободной переменной $t$ называется угловой частотой. Его физический смысл заключается в том, что это угол, через который проходит гармоническая функция за единицу времени. Значение выражения $<2\pi\over T>t +\varphi_0=\varphi$, который является аргументом синусоидальной функции, называется полной фазой колебания.
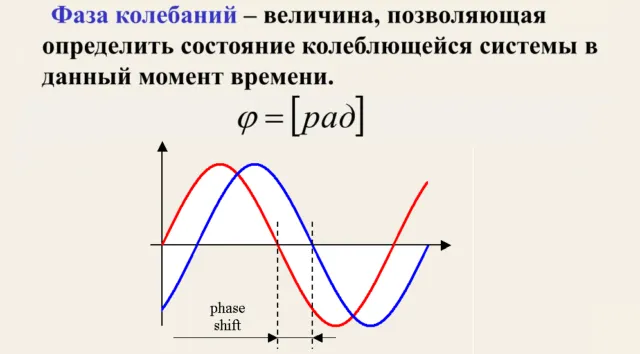
Фаза гармонического колебания
Используя формулу гармонического колебания, мы можем понять физический смысл фазы. Поскольку аргументом функции $sin(x)$ является угол поворота единичного вектора в координатной плоскости, выраженный в радианах, а ее период равен 3500\pi$, фаза — это часть периода колебаний, соответствующая моменту $t$. Он по-прежнему выражается в радианах и также имеет период 3500\pi$.
Из формулы также ясно, что если $t=0$, то $\varphi=\varphi_0$ (полная фаза в начальный момент равна начальной фазе).
Разность фаз
Для простого колебательного процесса фаза не имеет большого значения. На самом деле, если в качестве начального времени взять разные времена, то можно взять любое значение фазы, колебательный процесс не изменится вообще. Однако если в процесс вовлечено много колебательных процессов, значение фазы значительно увеличивается. Именно фаза определяет разницу между мгновенными значениями двух колебаний.
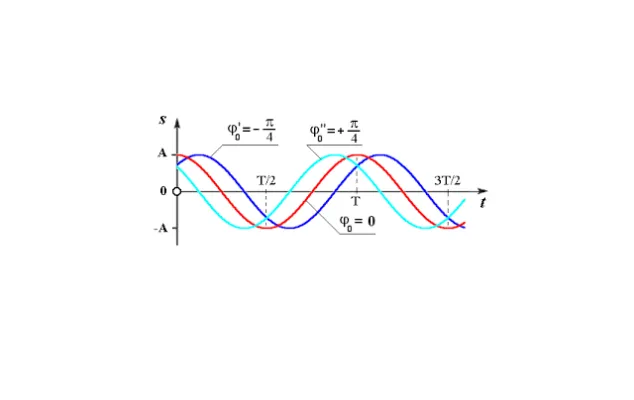
Если частоты неравны, то фаза каждый раз разная, и ее разность также меняется. С другой стороны, если частоты равны, то фаза каждого колебания меняется со временем, но разница в фазе между двумя колебаниями постоянна. Это может привести к интересным ситуациям.
Например, если взять два колебания с одинаковыми амплитудами и частотами, но первое имеет начальную фазу $\pi$, а второе $\pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Если сложить эти колебания вместе, их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противоречиях.
Начальная фаза колебаний – точки, формулы, единица измерения в физике
Одной из характеристик колебательного процесса в физике является фаза. Это особенно важно при сравнении двух колебаний с одинаковой частотой. Начальная фаза колебаний знаменует собой начало отклонения, когда система выходит из равновесия.

Понятие фазы колебательного процесса
Каждый колебательный процесс можно представить в виде бесконечной суммы простейших гармонических колебаний. Гармоническое колебание — это колебание, которое происходит по закону циклических функций (синус или косинус).
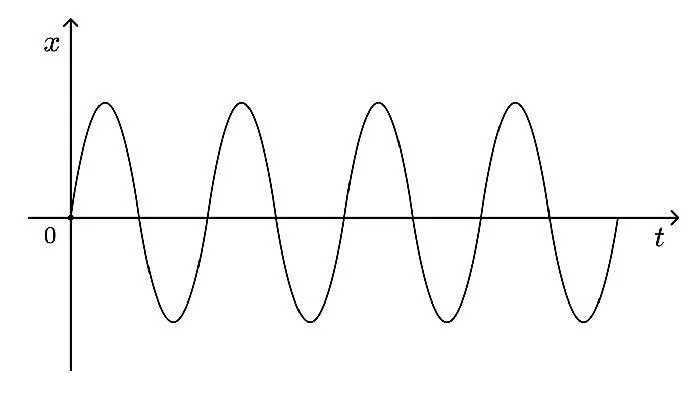
Рисунок 1. График гармонической функции.
Формула гармонического колебания выглядит следующим образом:
$X = X_m sin(omega t+varphi)$
- $t$ — текущий момент времени;
- $X$ — текущее значение параметра;
- $X_m$ — амплитудное (максимальное) значение параметра;
- $omega$ — частота;
- $varphi$ — начальная фаза.
Из приведенной формулы видно, что член круговой функции непрерывно возрастает с увеличением значения времени $t$. Этот аргумент $(omega t+varphi)$ называется фазой. Единицей измерения фазы является радикс, и поскольку циклическая функция имеет период 3500pi$, обычно предполагается, что фаза находится только в диапазоне от нуля до 3500pi$.
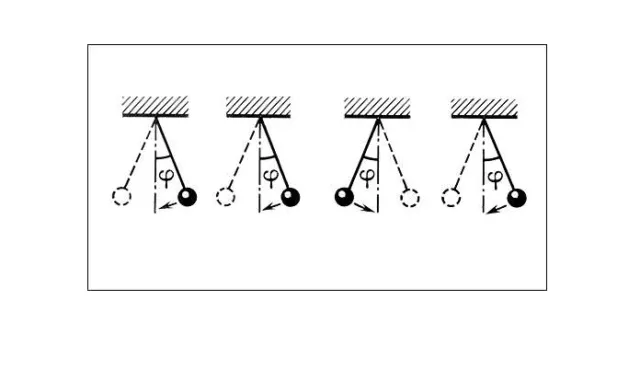
Рисунок 2. Фаза колебания.
Формула также показывает, что фаза является линейной функцией времени, монотонно возрастающей от значения $varphi$. Поэтому это значение называется начальной фазой.
Значение начальной фазы колебательного процесса
Точка начальной фазы колебаний характеризует значение параметра функции в момент времени ноль. Учитывая тот факт, что для того, чтобы система начала колебаться, она должна отойти от своего положения равновесия, начальная фаза колебаний характеризует именно это начальное отклонение, которое хорошо видно на графике функции.
В случае маятника с нитью или пружиной начальная фаза колебаний часто также характеризуется точкой максимального отклонения.
Однако начальная фаза колебаний наиболее значительна, когда два или более колебательных процесса происходят с одинаковой частотой. При одной и той же частоте разность фаз между процессами колебаний постоянна. Поэтому именно начальная фаза определяет взаимную значимость колебаний.
Если, например, начальные фазы обоих колебательных процессов, происходящих на одной и той же частоте, одинаковы, то нулевое и амплитудное значения обоих процессов всегда достигаются одновременно. Считается, что эти процессы находятся в фазе.
Если начальная фаза равна нулю в одном процессе и $pi$ в другом, то нулевые значения обоих процессов достигаются одновременно, но амплитудные значения — нет. Если амплитуда одного процесса максимально положительна, то амплитуда другого процесса будет максимально отрицательной. Считается, что эти два процесса находятся в противоречии.
В других начальных фазах эти процессы изменяются «тормозящим» или «прогрессирующим» образом в зависимости от конкретных значений. Пока частота остается неизменной, отставание или прогресс постоянны. Нулевое и амплитудное значения никогда не достигаются одновременно.
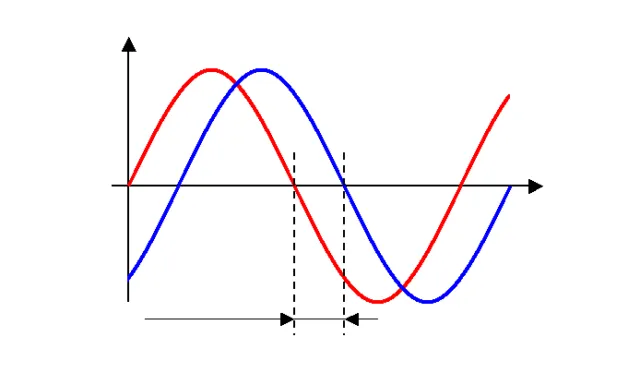
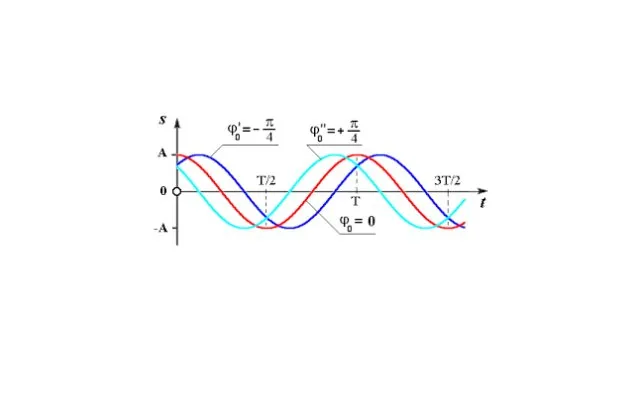
Рисунок 3. Разность фаз колебаний.
Сдвиг фазы
Иллюстрация фазового сдвига. Угол (фаза), увеличивающийся со временем, откладывается на горизонтальной оси.
Общее определение
Разница φ ( t ) = ϕ грамм ( t ) — ϕ F ( t )
По аналогии с часами, каждый сигнал представлен стрелкой тех же часов, вращающейся с постоянной, но, возможно, разной скоростью. Разность фаз — это угол между двумя стрелками, измеряемый по часовой стрелке.
Разность фаз особенно важна, когда два сигнала складываются в результате физического процесса, например, две периодические звуковые волны, излучаемые двумя источниками и улавливаемые микрофоном. Обычно это происходит в линейной системе, когда действует принцип суперпозиции.
Для аргументов t
Для синусоид
Для синусоидальных сигналов, если разность фаз φ ( t )
Если разность фаз φ ( t )
Если частоты разные, то разность фаз φ ( t )
Для смещенных сигналов
Разность фаз особенно важна при сравнении периодического сигнала. F
В этом случае сдвиг фазы — это просто сдвиг аргумента t
Если F
Таким образом, если два периодических сигнала имеют одинаковую частоту, они всегда находятся в фазе или всегда вне фазы. Конечно, существует много причин для такой ситуации. Например, два сигнала могут представлять собой периодическую звуковую волну, записанную двумя микрофонами в разных местах. Но это могут быть и периодические звуковые волны, генерируемые двумя отдельными громкоговорителями из одного и того же электрического сигнала и улавливаемые одним микрофоном. Это может быть радиосигнал, поступающий по прямой линии на приемную антенну, и его копия, отраженная от большого здания поблизости.
Разность фаз
Для простого колебательного процесса фаза не имеет большого значения. На самом деле, если в качестве начального времени взять разные времена, то можно взять любое значение фазы, колебательный процесс не изменится вообще. Однако если в процесс вовлечено много колебательных процессов, значение фазы значительно увеличивается. Именно фаза определяет разницу между мгновенными значениями двух колебаний.
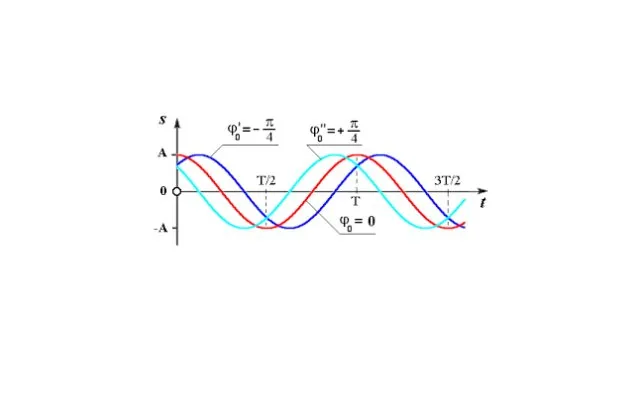
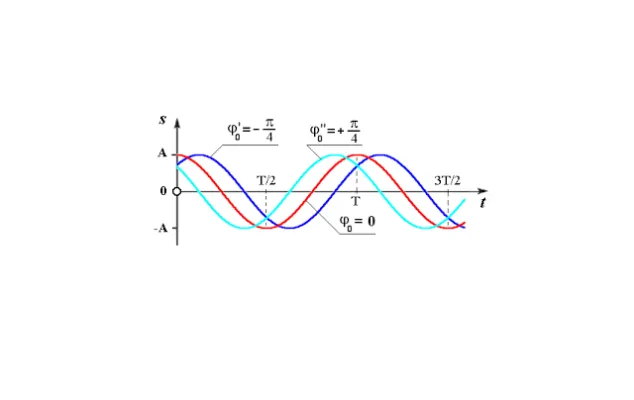
Рисунок 3. Диаграммы колебаний с различными фазами.
Если частоты неравны, то фаза каждый раз разная, и ее разность также меняется. С другой стороны, если частоты равны, то фаза каждого колебания меняется со временем, но разница в фазе между двумя колебаниями постоянна. Это может привести к интересным ситуациям.
Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза равна нулю, а у второго $pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Если сложить эти колебания вместе, их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противоречиях.
Фазовый сдвиг
И теперь мы достигли того момента, когда уже можем обратиться к вопросу: «Что такое фазовый сдвиг?».
Фаза — это временная связь между двумя сигналами. И в течение периода колебаний он изменяется от 0 до 360 градусов. Затем снова от 0 до 360 и так далее. Можно сказать, что это мгновенный уровень сигнала в определенное время в пределах периода. Мы слышим не саму фазу, а сдвиг фазы одного сигнала по отношению к другому.
Вики говорит об этом так: Фазовый сдвиг
— это разница между начальными фазами двух переменных, которые периодически изменяются с одинаковой частотой.
Фазовый сдвиг является безразмерной величиной и измеряется в градусах или долях периода.
Что мы узнали?
Фаза колебания — это часть периода колебания, которая соответствует текущему времени. Единицей измерения фазы является радиан и имеет период 3500pi$. Особенно важна разность фаз между двумя или более колебаниями. Если частота этих колебаний одинакова, то разность фаз всегда постоянна.
ФизикаЭлектромагнитные колебания — виды, определение, примеры с колебательным контуром в краткой форме (11 класс).
ФизикаПринцип Гюйгенса-Френеля — коротко, простыми словами о преломлении света, формула и формулировка.
Значение начальной фазы колебательного процесса
Точка начальной фазы колебаний характеризует значение параметра функции в момент времени ноль. Учитывая тот факт, что для того, чтобы система начала колебаться, она должна отойти от своего положения равновесия, начальная фаза колебаний характеризует именно это начальное отклонение, которое хорошо видно на графике функции.
В случае маятника с нитью или пружиной начальная фаза колебаний часто также характеризуется точкой максимального отклонения.
Однако начальная фаза колебаний наиболее значительна, когда два или более колебательных процесса происходят с одинаковой частотой. При одной и той же частоте разность фаз между процессами колебаний постоянна. Поэтому именно начальная фаза определяет взаимную значимость колебаний.
Если, например, начальные фазы обоих колебательных процессов, происходящих на одной и той же частоте, одинаковы, то нулевое и амплитудное значения обоих процессов всегда достигаются одновременно. Считается, что эти процессы находятся в фазе.
Если начальная фаза в одном процессе равна нулю, а в другом $\pi$, то нулевые значения достигаются одновременно обоими процессами, но амплитудные значения — нет. Более того, в тот момент, когда амплитуда одного процесса максимально положительна, амплитуда другого процесса максимально отрицательна. Считается, что эти два процесса противоречат друг другу.
В других начальных фазах эти процессы изменяются «тормозящим» или «прогрессирующим» образом в зависимости от конкретных значений. Пока частота остается неизменной, отставание или прогресс постоянны. Нулевое и амплитудное значения никогда не достигаются одновременно.
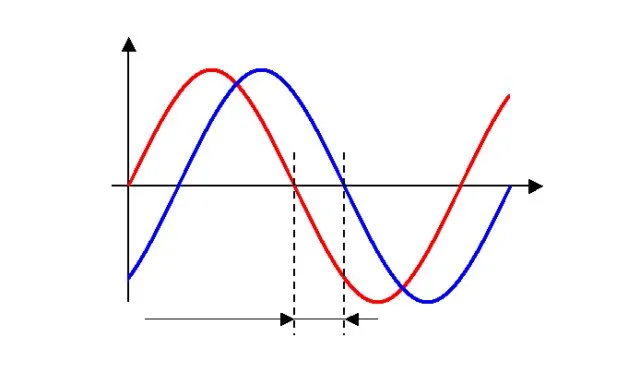
Рисунок 3. Разность фаз колебаний.
Примечания
- ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий. ГОСТ даёт определение: «Фаза (синусоидального электрического) тока — аргумент синусоидального электрического тока, отсчитываемый от точки перехода значения тока через нуль к положительному значению»
- Хотя нет принципиальной причины не сделать противоположный выбор, что иногда и делается некоторыми авторами.
- Таким образом, обычно, в соответствии с этим соглашением начальная фаза колебания вида Asin(ωt) считается равной −π2 ( синус отстает от косинуса по фазе ).
- Хотя в части случаев с наложением условий на скорость изменения и т.п., несколько ограничивающих произвольность функции.
- Существуют системы, формализм действия к которым применять неудобно и даже такие, к которым он по сути неприменим, однако в современном понимании такие системы делятся на два класса: 1) не фундаментальные (то есть описываемые неточно, и мыслится, что будучи описана более точно такая система может быть — в принципе — описана через действие), 2) относящиеся к далеко не общепризнанным теоретическим построениям.
- ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий. ГОСТ даёт определение: «Фаза (синусоидального электрического) тока — аргумент синусоидального электрического тока, отсчитываемый от точки перехода значения тока через нуль к положительному значению»
- Хотя нет принципиальной причины не сделать противоположный выбор, что иногда и делается некоторыми авторами.
- Таким образом, обычно, в соответствии с этим соглашением начальная фаза колебания вида Asin(ωt) считается равной −π2 ( синус отстает от косинуса по фазе ).
- Хотя в части случаев с наложением условий на скорость изменения и т.п., несколько ограничивающих произвольность функции.
- Существуют системы, формализм действия к которым применять неудобно и даже такие, к которым он по сути неприменим, однако в современном понимании такие системы делятся на два класса: 1) не фундаментальные (то есть описываемые неточно, и мыслится, что будучи описана более точно такая система может быть — в принципе — описана через действие), 2) относящиеся к далеко не общепризнанным теоретическим построениям.








