Эпициклоида в астрономии как попытка объяснить движение планет. Эпицикл это в астрономии.

С более точными наблюдениями использовались дополнительные эпициклы и куспиды для представления новых наблюдаемых явлений, пока в конце Средневековья Вселенная не стала «сферой / с очерченными центрами и куспидами, / кругом и эпициклом, сферой внутри сферы».

Эпицикл это в астрономии

Гениальный ученый Галилео Галилей посвятил свою жизнь различным областям науки. Сначала он проводил астрономические наблюдения, благодаря которым сделал удивительные открытия о фазах Венеры, спутниках Юпитера, неровной поверхности Луны и солнечных пятнах. Во-вторых, он исследовал движение тел, тем самым бросив вызов всей аристотелевской физике, которая доминировала в западной науке на протяжении 2000 лет. Но главной заслугой ученого, оставившей величайший след в истории, была его готовность, даже под угрозой смерти на костре, отстаивать новый способ изучения мира — научный метод, основанный на эмпирических фактах и математической точности.

ЭПИЦИКЛ И ДЕФЕРЕНТ

Епископы и девианты — один из ярчайших примеров изобретательности, с которой греки решали, казалось бы, непреодолимые проблемы. Птолемей и другие древние астрономы были абсолютно уверены, что планеты движутся по кругу. Однако наблюдение за небом в определенное время года привело к невероятным результатам. Планеты, которые двигались вперед в течение нескольких ночей наблюдений, в конце концов останавливались или начинали двигаться назад и только потом продолжали двигаться вперед. Математические и геометрические уловки помогли решить проблему.

В III веке до н.э. Гиппарху пришла в голову гениальная идея объединить различные круговые движения, чтобы объяснить эту странную кривизну. По его мнению, планеты вращаются вокруг Земли по двум окружностям: первая называется эпициклом, а их центр вращается вокруг Земли по второй окружности, вторичной (рис. 1). Эта комбинация показывает, что орбита планеты описывает несколько петель, прежде чем совершить полный оборот вокруг Земли (рис. 2). Птолемей также использовал эту умную идею и добавил эпициклы, называемые малыми эпициклами, чтобы достичь максимальной точности для определенных орбит, например, Солнца.

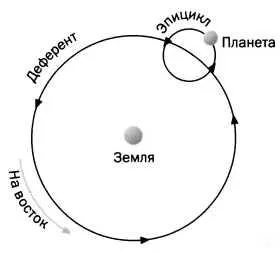
РИС. 1

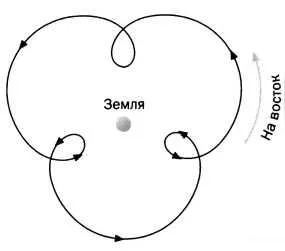
РИС. 2

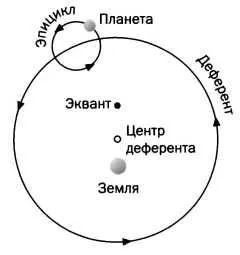
РИС. 3

Чтобы объяснить ретроградное движение планет, Птолемей предположил, что они движутся вокруг Земли, совмещая две круговые орбиты — вторичную и перициклическую (рис. 1). Поэтому планета должна была описать несколько кругов, прежде чем совершить полный оборот вокруг Земли (рис. 2). Наблюдаемые орбитальные аномалии были объяснены эксцентриситетом Земли относительно центра (рис. 3). Более того, постоянную угловую скорость, с которой, как утверждалось, движутся планеты, можно было наблюдать только из некоторых воображаемых точек — экваторов, но не с Земли.

Что такое эпициклои­да и как она забралась на небо?

Но нам это легко, потому что в наших знаниях нас поддерживает наука, математические расчеты и, наконец, возможность практически «потрогать» Солнечную систему руками с помощью космических кораблей и межпланетных станций. А вы пытаетесь объяснить движение небесных тел по небу, имея лишь «плоскую» картинку неба над головой и не имея простейшего телескопа!

В таком незавидном положении астрономы находились на протяжении большей части истории.

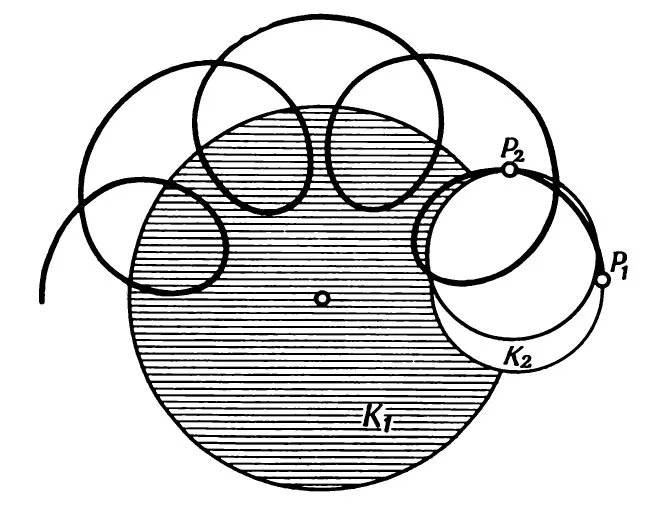
Как представляли себе систему движения планет вокруг Земли в Средние века. Не просто орбита, а целая эпициклика!

Подумайте об этом: Если описать движение небесных тел так, как оно представляется наблюдателю с Земли, то получится совершенно непонятная картина. А если рассматривать Землю как неподвижное тело (которая является центром Вселенной!), то трудно установить единый принцип для движения звезд и планет.

Хотя со звездами все понятно. Для наблюдателя Земли — центра Вселенной — они постоянно вращаются вокруг нее. Но Луна и планеты ведут себя непостижимым образом!

Иногда они бегут впереди или позади солнца, а иногда выглядят так, будто «катятся» по небу в противоположном направлении. Чтобы объяснить, почему планеты и Луна то опережают, то отстают от Солнца в своем видимом движении по небу, древние астрономы приняли за факт сценарий, согласно которому Луна и планеты движутся по особым орбитам, называемым эпициклическими.

Насколько точной была модель с эпициклоидами объясняющими движение планет

Эпицикл — это плоская кривая, образованная фиксированной точкой на окружности, «катящейся» наружу к другой окружности, своего рода «петля» на окружности.

Такая петля образуется, когда центр окружности K₂(называемый эпициклом) движется с постоянной скоростью по окружности другой окружности K₁(называемый деферентом) и диск K₂вращается равномерно. Таким образом, когда меньшая окружность проходит определенное расстояние по окружности большей окружности, точка P₁окружности эпицикла перемещается в новое положение P_2.

И самое интересное, что эта модель, хотя и не совсем верная, может достаточно хорошо объяснить видимый ход планет. По крайней мере, хаос был устранен.

Конечно, для достижения лучшего соответствия между теорией и практическими наблюдениями была необходима целая система проверок и дополнительных допущений. Например, нужно было предположить, что Земля не находится точно в центре вторичного круга и что планеты движутся по вторичным эпициклам, которые, в свою очередь, движутся по первичным эпициклам.

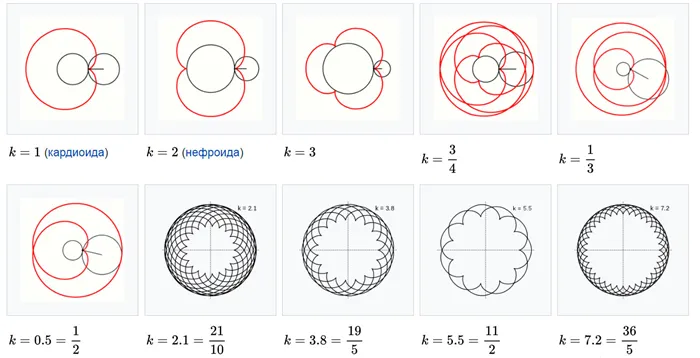
В Википедии приведено несколько классических типов эпициклов, отличающихся взаимными размерами образующих их тел.

Так возникли эпициклы, картина стала невероятно запутанной, но все же вполне понятной для опытных людей и достаточно хорошо отражает то, как все устроено. Проще говоря, это была довольно хорошая модель, которая была доведена до пригодного для использования состояния с помощью ряда допущений и корректировок.

В результате созданная Птолемеем (90-160 гг. н.э.) система с Землей в центре Вселенной успешно сохранялась на протяжении 1,5 тысяч лет, и не только при последнем повороте событий, потому что такая система устраивала церковь, обладавшую огромной властью в Средние века.

Почему Коперник проиграл Птолемею

Поэтому попытка Николая Коперника (1473-1543) свергнуть Птолемееву систему и заменить ее радикально иной теорией была в то время высшей смелостью, настоящим вызовом небесам! Коперник поместил Солнце в центр системы планет, вращающихся вокруг Солнца по круговой траектории, значительно упростив таким образом систему. Сложные циклы движения (настоящая алхимия!) были заменены аккуратными кругами.

Все было настолько просто, что идея Коперника многим казалась бессмыслицей. Сегодня все согласны с тем, что «ученые старой школы» и церковники были в ярости от того, что он вырвал у них ковер из-под ног. Но на самом деле все было гораздо проще: как ни парадоксально, но довольно «грубая» теория Коперника изначально просто подчинялась теории движения планет по эпициклам, которая совершенствовалась веками.

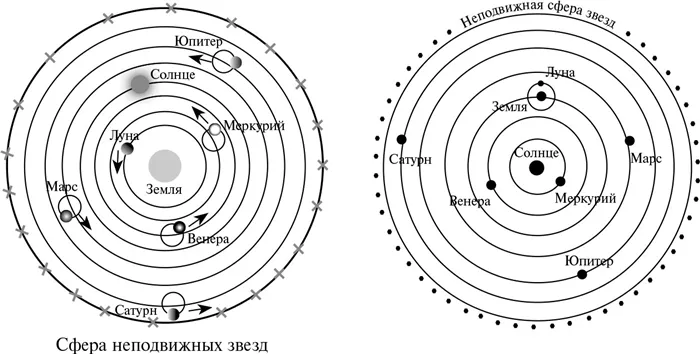
Модель Солнечной системы Птолемея (слева) и Коперника (справа). Хотя Коперник был прав «в целом», его теория не могла объяснить всего.

Положения планет, рассчитанные на основе теории Коперника, не совсем соответствовали реальным наблюдениям. А закон движения, который не дает точных результатов, не может удовлетворить ученого, и даже такой великий астроном того времени, как Тихо Браге, не был убежден в правильности системы Коперника.

Поэтому тот факт, что старая и ошибочная система не рухнула сразу, объясняется не «средневековым невеждой», а слабой доказательной базой «новой и передовой» системы. Только через двенадцать лет ученик Тихо Браге, Иоганн Кеплер, завершил систему Коперника, установив свои знаменитые законы, и только тогда ошибка использования эпициклов в астрономии для объяснения движения планет стала очевидной для всех.

Источник: Для starcatalog.ru, по материалам книги «Физика в космосе» Гельмута Линдера, 1964 год.

Теория относительности

С изобретением масс-спектрографа стало возможным измерять массу отдельных атомных ядер с такой точностью, что закон сохранения массы перестал действовать. Устройство было разработано английским физиком

ТЕОРИЯ МЕХАНИЗМА В рассматриваемый период в России была основана теория одной из важнейших подотраслей техники — теория механизма. Это было сделано П.Л. Чебышевым в середине XIX века. В области математики он добился фундаментальных результатов в

ТЕОРИЯ КОРАБЛЯ

Помимо баллистики, теория корабля была еще одной важной областью техники, в развитии которой русские ученые принимали значительное участие. В рассматриваемый период теория кораблей развивалась в основном в военно-морском флоте

СТРОГО ТЕОРИЯ В отличие от авторов моделей, физики-теоретики, больше увлекающиеся математикой, стараются начать с чистой теории. Можно надеяться начать с единой элегантной теории; только отделив следствия теории, можно доработать ее.

1. Теория струн

Квантовая механика и теория гравитации в рамках общей теории относительности, как правило, работают очень плохо. С практической точки зрения, квантовая теория гравитационного взаимодействия, как правило, не является

М — теория Принстонский физик Эдвард Виттен говорит: «М означает «магия» или «мембрана», в зависимости от того, что вы хотите. Некоторые более ранние теории оказываются частными случаями этой общей теории — так называемые теории струн, суперструн и мембран. Вместо

Эпициклы

Одна из школ астрономической истории предполагает, что незначительные ошибки в первоначальной системе Птолемея были обнаружены в результате наблюдений, собранных с течением времени. Ошибочно считалось, что в модели были добавлены дополнительные уровни эпициклов (круги внутри кругов) для лучшего учета наблюдаемых движений планет. Считается, что умножение эпициклов привело к тому, что к XVI веку система стала практически неработоспособной, и именно Коперник создал свою гелиоцентрическую систему, чтобы упростить астрономию времен Птолемея, резко сократив количество циклов.

С более точными наблюдениями использовались дополнительные эпициклы и куспиды для представления новых наблюдаемых явлений, пока в конце Средневековья Вселенная не стала «сферой / с очерченными центрами и куспидами, / кругом и эпициклом, сферой внутри сферы».

— Дороти Стимсон, Постепенное принятие коперниканской теории Вселенной, 1917 18

Как мера сложности, у Птолемея число кругов равно 80, а у Коперника — только 34.19 Самое большое число появилось в 1960-х годах в Британской энциклопедии астрономии при обсуждении интереса кастильского короля Альфонса X к астрономии в XIII веке (Альфонсу приписывают заказ Альфонсинской скрижали).

До этого времени у каждой планеты было от 40 до 60 эпициклов, которые так или иначе отражали ее сложное движение между звездами. Впечатленный сложностью работы, Альфонсо отметил, что если бы он присутствовал при ее создании, то мог бы дать отличный совет.

Основная проблема этой теории эпициклов заключается в том, что историки, изучавшие книги по средневековой и ренессансной птолемеевской астрономии, не нашли никаких свидетельств использования нескольких эпициклов для каждой планеты. Например, таблицы Альфонсина, очевидно, были рассчитаны с использованием оригинальных, нерасчетных методов Птолемея. 21 Еще одна проблема заключается в том, что сами модели не поощрялись. В дифференциальной и эпициклической моделях части множества соединены. Изменение одного параметра для улучшения подгонки в одной точке разрушает подгонку в другой точке. Модель Птолемея, вероятно, оптимальна в этом отношении. Он дал в целом хорошие результаты, но в некоторых моментах промахнулся. Опытные астрономы признали бы эти недостатки и приняли их во внимание.

Математический формализм

Ни в одной области астрофизики или наблюдательной астрономии нет двусторонней симметричной или эксцентричной периодической кривой, которую нельзя было бы нарисовать как результирующее движение точки, вращающейся в созвездии из конечного числа эпициклов, вращающихся вокруг фиксированного дефлектора.

— Норвуд Рассел Хансон, Математическая сила эпициклической астрономии, 1960. 22

Любой путь, периодический или нет, замкнутый или открытый, может быть представлен бесконечным числом эпициклов. Это связано с тем, что эпициклы могут быть представлены в виде комплексных рядов Фурье; таким образом, при большом количестве эпициклов, очень сложные траектории могут быть представлены в комплексной плоскости. 23 Дано комплексное число

где а₀и к₀константы, i = √ -1 — мнимая единица, а t — время, соответствующее разности, центрированной в начале комплексной плоскости и вращающейся с радиусом α.₀и угловая скорость

Где T — период. Если z₁— является орбитой эпицикла, тогда дифференциал плюс эпицикл задается в виде суммы
z 2 = z 0 + z 1 = a 0 e y k 0 t + a 1 e y k 1 t .= z_ + z_ = a_ e ^+ a_ e ^,.>

Это квазипериодическая функция и только периодическая функция, если отношение постоянных k_jявляется рациональным. Обобщение на N эпициклов дает квазипериодическую функцию.

Логика может быть использована двумя способами для обоснования точки зрения: во-первых, для обеспечения достаточного доказательства принципа. Логика используется и по-другому, не как достаточное доказательство принципа, а как доказательство уже установленного принципа, показывающее согласованность его результатов, подобно тому, как в астрономии теория эксцентриситетов и эпициклов считается установленной, потому что она может объяснить логические явления небесных движений; но не так, как если бы это доказательство было достаточным, потому что другая теория могла бы объяснить это.

Плохая наука

В то время как под «гипотезой» мы понимаем экспериментальную теорию, которая еще не проверена, Птолемей обычно подразумевает под гипотезой нечто иное, чем «модель», «объяснительную систему», часто ссылаясь на «гипотезы, которые мы доказали».

Коперник добавил дополнительный эпицикл к своим планетам, но только для того, чтобы устранить эквивалент Птолемея, который он считал философским отклонением от аристотелевского совершенства небес. Математически второй эпицикл и равенство приводят к одинаковым результатам, и многие астрономы-коперниканцы до Кеплера продолжали использовать равенство, потому что математика была проще.

Математический формализм

Ни одна бисимметричная или эксцентрично-периодическая кривая не используется в астрофизике или наблюдательной астрономии, которая не может быть гладко представлена как результирующее движение точки, вращающейся в созвездии конечного числа эпициклов, вращающихся вокруг постоянной дивергенции.

— Норвуд Рассел Хэнсон, «Математическая сила» эпициклической астрономии», 1960 г.

Любой путь, периодический или нет, замкнутый или открытый, может быть представлен бесконечным числом эпициклов.

Это связано с тем, что эпициклы могут быть представлены в виде комплексных рядов Фурье; таким образом, при большом количестве эпициклов, очень сложные траектории могут быть представлены в комплексной плоскости.

Пусть комплексное число будет

, где a 0 и k 0 — константы, i = √ − 1 — мнимая единица, а t — время, соответствует отклонению с центром в начале комплексной плоскости и вращающемуся с радиусом a 0 и угловой скоростью k 0 = 2 π T, =>\,,>

Если z 1 является траекторией эпицикла, то дифференциал плюс эпицикл представляется в виде суммы

z 2 = z 0 + z 1 = a 0 eik 0 t + a 1 eik 1 t. = z_ + z_ = a_ e ^+ a_ e ^\,.>

Это квазипериодическая функция и периодическая функция, если отношение постоянных k j рационально. Обобщение на N эпициклов дает квазипериодическую функцию

которая является периодической, если каждая пара k j рационально связана. Поиск коэффициентов a j для представления зависящей от времени траектории в комплексной плоскости, z = f (t), является целью воспроизведения траекторий с отклонениями и эпициклов, и это путь к «спасению явлений» (Rettung der Phänomene).

Этот параллелизм был замечен Джованни Скиапарелли. В контексте дискуссии о «спасении явлений в сравнении с предложением объяснений» в эпоху Коперниканской революции можно понять, почему Фома Аквинский в тринадцатом веке был так озабочен «спасением явлений»:

Логика может использоваться двумя способами для утверждения точки зрения: во-первых, для обеспечения достаточного доказательства принципа. Логика используется и по-другому, не для того, чтобы обеспечить достаточное доказательство принципа, а для подтверждения уже установленного принципа, показывая согласованность его результатов, подобно тому, как в астрономии теория эксцентриситетов и эпициклов считается установленной, потому что она может объяснить логические явления небесных движений; но не так, как если бы это доказательство было достаточным, потому что другая теория могла бы объяснить это.

Плохая наука

Отчасти из-за непонимания того, как работают различные/эпициклические модели, «добавление эпициклов» в современном научном дискурсе используется уничижительно. Например, этот термин может использоваться для описания постоянных усилий по корректировке теории, чтобы ее предсказания соответствовали фактам. Принято считать, что дополнительные цензоры были разработаны для уменьшения возрастающих ошибок в птолемеевой системе по мере того, как измерения становились все более точными, особенно для Марса. Согласно этому мнению, циркуляры рассматриваются некоторыми как парадигма плохой науки. Отчасти проблема может заключаться в том, что эпицикл неправильно понимается как объяснение движения тела, а не простое описание. Тумер объясняет следующее:

Если под «гипотезой» мы понимаем предварительную теорию, которая еще не проверена, то Птолемей обычно подразумевает под гипотезой скорее «модель», «объяснительную систему», часто даже говоря о «гипотезах, которые мы доказали»».

— Г. Дж. Тумер, Альмагест Птолемея, 1998 г.

Коперник добавил дополнительный эпицикл к своим планетам, но только для того, чтобы устранить эквивалент Птолемея, который он считал философским отклонением от аристотелевского совершенства небес. Математически второй эпицикл и равенство приводят к одинаковым результатам, и многие астрономы-коперниканцы до Кеплера продолжали использовать равенство, потому что математика была проще.

См. Также

В Викискладе есть материалы, связанные с Эпицикл.

• Система Птолемея — в проекте Galileo Университета Райса
• Эксцентрики, отклоняющиеся, эпициклы и экванты в MathPages

Анимированные иллюстрации

• Java-моделирование Система Птолемея — в Анимационном виртуальном планетарии Пола Стоддарда, Университет Северного Иллинойса.
• Демонстрация эпициклов и зависимостей — на веб-сайте Розмари Кеннетт в Университете Сиракуз. различные планеты.
• Апплет, показывающий принцип эпицикла, с параллельным сравнением геоцентрической и гелиоцентрической моделей.
• Превосходная презентация Птолемея, Коперника, Браге и Кеплера, основанный на трудах Кеплера. В Части 1 исследуются различные системы и их эквивалентность, в Частях 2 и далее исследуется вывод Кеплера его законов.
• Птолемей и Гомер (Симпсон) Реконструкция причудливой орбиты планеты с помощью системы эпициклов и исходных элементов Птолемея.

Плохая наука править

Отчасти из-за непонимания того, как работают вторичные/эпициклические модели, «добавление эпициклов» в современном научном дискурсе используется уничижительно. Этот термин может использоваться, например, для описания постоянных усилий по корректировке теории, чтобы ее предсказания соответствовали фактам. Принято считать, что дополнительные эпициклы были разработаны для уменьшения возрастающих ошибок в птолемеевой системе по мере того, как измерения становились все более точными, особенно для Марса. Согласно этой точке зрения, эпициклы рассматриваются некоторыми как парадигма плохой науки. 28 Отчасти проблема может заключаться в том, что эпициклы неправильно понимаются не как простое описание, а как объяснение движения тела. Тумер объясняет следующее:

Если под «гипотезой» мы понимаем предварительную теорию, которая еще не проверена, то Птолемей обычно понимал под гипотезой нечто большее, чем «модель», «объяснительная система», и часто даже подразумевал «гипотезы, которые мы доказали».

Коперник добавил дополнительный эпицикл к своим планетам, но только для того, чтобы устранить птолемеевский эквивалент, который он считал философским отклонением от аристотелевского совершенства небес. Математически второй эпицикл и равенство приводят к одинаковым результатам, и многие астрономы-коперниканцы до Кеплера продолжали использовать равенство, потому что математика была проще.

См. Также править

1. ^ «эпицикл». Интернет-словарь этимологии .
2. ^ Андреа, Муршель (1995). «Структура и функция физических гипотез Птолемея о движении планет». Журнал истории астрономии (xxvii): 33–61. Bibcode : 1995JHA. 26. 33M. Проверено 2 августа 2014 .
3. ^ Пример сложности проблемы см. В Owen Gingerich, The Book Nobody Read, Walker, 2004, p. 50
4. ^ Gingerich, Глава 4
5. ^ Один том De Revolutionibus был посвящен описанию тригонометрии, используемой для преобразования между геоцентрическими и гелиоцентрическими координатами.
6. ^ Gingerich, стр. 267
7. ^ Gingerich, стр. 54
8. ^ Палтер, Роберт (1970). «Подход к истории астрономии». Исследования по истории и философии науки. 1 : 94.
9. ↑ Оуэн Джинджерич, «Альфонсо X как покровитель астрономии», в книге «Глаз неба: Птолемей, Коперник, Кеплер» (Нью-Йорк: Американский институт физики, 1993), стр. 125.
10. ^ Gingerich, «Кризис против эстетики в революции Коперника», в глаз Небесной, стр. 193-204.
11. ^ «Распространенное мнение, что гелиоцентрическая система Коперника представляет собой значительное упрощение системы Птолемея, очевидно, неверно. T Сами модели Коперника требуют примерно вдвое больше кругов, чем модели Птолемея, и они гораздо менее элегантны и адаптируемы». Нойгебауэр, Отто (1969) 1957. Точные науки в древности (2-е изд.). Dover Publications. ISBN978-0-486-22332-2., п. 204. Это крайняя оценка в пользу Птолемея.
12. ^ Кестлер, Артур (1989) 1959. Лунатики. Аркана, Penguin Books., п. 195
13. ^ Хитрить, подход к истории астрономии, стр. 113-114.
14. ^ Кестлер, Артур (1989) 1959. Лунатики. Аркана, Penguin Books., стр. 194–195
15. ^ Модель деферента / эпицикла фактически используется для вычисления положения Луны, необходимого для определения современных индуистских календарей. См. Нахум Дершовиц и Эдвард М. Рейнгольд: Календарные вычисления, Cambridge University Press, 1997, Глава 14. ( ISBN0-521-56474-3 )
16. ^ Голдштейн, Бернард Р. (1972). «Теория и наблюдения в средневековой астрономии». Исида. 63 (1): 39–47 40–41. DOI : 10.1086 / 350839 .
17. ^ Коллерстр, Николай (2000). Забытая лунная теория Ньютона. Green Lion Press. ISBN1-888009-08-X .
18. ^ Дороти Стимсон, Постепенное принятие теории Вселенной Коперника. (Нью-Йорк, 1917), стр.14 .. Цитата из« Потерянного рая» Джона Мильтона, книга 8, 11.82–85.
19. ^ Роберт Палтер, подход к истории ранней астрономии
20. ↑ Британская энциклопедия, 1968, т. 2, стр. 645. Это определяется как наибольшее число в Owen Джинджерича, Альфонсо X. Джинджерич также выразила сомнение по поводу цитаты, приписываемой Альфонсо. Однако в «Книге, которую никто не читал» (стр. 56) Джинджерих рассказывает, что он бросил вызов Encyclopdia Britannica по поводу количества эпициклов. Они ответили, что первоначальный автор записи умер, и ее источник не может быть подтвержден.
21. ^ Gingerich, Книга Nobody чтения, стр. 57
22. ^ Хэнсон, Норвуд Рассел (1 июня 1960). «Математическая сила эпициклической астрономии» (PDF). Исида. 51 (2): 150–158. DOI : 10.1086 / 348869. ISSN0021-1753. JSTOR226846. Проверено 21 октября 2011 года .
23. ^ См., Например, эту анимацию, созданную Кристианом Карманом и Рамиро Серра, в которой используется 1000 эпициклов для прослеживания мультипликационного персонажа Гомера Симпсона ; ср. также « Deferentes, epiciclos y adapaciones » Кристиана Кармана. и «La refutabilidad del Sistema de Epiciclos y Deferentes de Ptolomeo» .
24. ^ Ср. Дюгем, Пьер (1969). Чтобы спасти явления, написано эссе по идее физической теории от Платона до Галилея. Чикаго: Издательство Чикагского университета. OCLC681213472. ( отрывок ).
25. ^ Джованни Галлавотти: » Квазипериодические движения от Гиппарха до Колмогорова». В: Rendiconti Lincei — Matematica e Applications. Series 9, Band 12, No. 2, 2001, с. 125–152 ( PDF; 205 КБ )
26. ^ Лучио Руссо: забытая революция. Как зародилась наука в 300 г. до н.э. и почему ей пришлось возродиться. Спрингер, Берлин. 2004, ISBN3-540-20068-1, стр. 91.
27. ^ Summa Theologica, I кв. 32 а. 1 объявление 2
28. ^ См., Например, Kolb, Rocky, Blind Watchers of the Sky, Addison – Wesley, 1996. P. 299 ( ISBN0-201-48992-9 )
29. ^ Toomer, GJ (1998). Альмагест Птолемея. Издательство Принстонского университета. п. 23. ISBN0-691-00260-6 .

Математический формализм

Ни в одной области астрофизики или наблюдательной астрономии нет двусторонней симметричной или эксцентричной периодической кривой, которую нельзя было бы нарисовать как результирующее движение точки, вращающейся в созвездии из конечного числа эпициклов, вращающихся вокруг фиксированного дефлектора.

— Норвуд Рассел Хансон, Математическая сила эпициклической астрономии, 1960. 22

Любой путь, периодический или нет, замкнутый или открытый, может быть представлен бесконечным числом эпициклов. Это связано с тем, что эпициклы могут быть представлены в виде комплексных рядов Фурье; таким образом, при большом количестве эпициклов, очень сложные траектории могут быть представлены в комплексной плоскости. 23 Дано комплексное число

где а₀и к₀константы, i = √ -1 — мнимая единица, а t — время, соответствующее разности, центрированной в начале комплексной плоскости и вращающейся с радиусом α.₀и угловая скорость

Где T — период. Если z₁— является орбитой эпицикла, тогда дифференциал плюс эпицикл задается в виде суммы
z 2 = z 0 + z 1 = a 0 e y k 0 t + a 1 e y k 1 t .= z_ + z_ = a_ e ^+ a_ e ^,.>

Это квазипериодическая функция и только периодическая функция, если отношение постоянных k_jявляется рациональным. Обобщение на N эпициклов дает квазипериодическую функцию.

Логика может быть использована двумя способами для обоснования точки зрения: во-первых, для обеспечения достаточного доказательства принципа. Логика используется и по-другому, не как достаточное доказательство принципа, а как доказательство уже установленного принципа, показывающее согласованность его результатов, подобно тому, как в астрономии теория эксцентриситетов и эпициклов считается установленной, потому что она может объяснить логические явления небесных движений; но не так, как если бы это доказательство было достаточным, потому что другая теория могла бы объяснить это.

Плохая наука

В то время как под «гипотезой» мы понимаем экспериментальную теорию, которая еще не проверена, Птолемей обычно подразумевает под гипотезой нечто иное, чем «модель», «объяснительную систему», часто ссылаясь на «гипотезы, которые мы доказали».

Коперник добавил дополнительный эпицикл к своим планетам, но только для того, чтобы устранить эквивалент Птолемея, который он считал философским отклонением от аристотелевского совершенства небес. Математически второй эпицикл и равенство приводят к одинаковым результатам, и многие астрономы-коперниканцы до Кеплера продолжали использовать равенство, потому что математика была проще.

Смотрите также

1. ^ «эпицикл». Интернет-словарь этимологии .
2. ^ Андреа, Муршель (1995). «Структура и функция физических гипотез Птолемея о движении планет». Журнал истории астрономии (xxvii): 33–61. Bibcode:1995JHA. 26. 33M. Получено 2 августа 2014 .
3. ^ Пример сложности проблемы см. В Owen Gingerich, Книга, которую никто не читал, Уокер, 2004, стр. 50
4. ^ Gingerich, Глава 4
5. ^ Один том De Revolutionibus был посвящен описанию тригонометрии, используемой для преобразования между геоцентрическими и гелиоцентрическими координатами.
6. ^ Gingerich, p. 267
7. ^ Gingerich, p. 54
8. ^ Палтер, Роберт (1970). «Подход к истории астрономии». Исследования по истории и философии науки. 1 : 94.
9. ^ Оуэн Джинджерич, «Альфонсо X как покровитель астрономии», в Око Небесное: Птолемей, Коперник, Кеплер (Нью-Йорк: Американский институт физики, 1993), стр. 125.
10. ^ Гингерич, «Кризис против эстетики в Коперниканской революции», в Глаз Неба С. 193–204.
11. ^ «Распространенное мнение о том, что гелиоцентрическая система Коперника представляет собой значительное упрощение системы Птолемея, очевидно, неверно. Сами модели Коперника требуют примерно вдвое больше кругов, чем модели Птолемея, и они гораздо менее элегантны и адаптируемы». Нойгебауэр, Отто (1969) 1957. Точные науки в древности (2-е изд.). Dover Publications. ISBN978-0-486-22332-2 .
12. , п. 204. Это крайняя оценка в пользу Птолемея.
13. ^ Кестлер, Артур (1989) 1959. Лунатики. Аркана, Книги о пингвинах.
14. , п. 195
15. ^ Палтер, Подход к истории астрономии С. 113–114.
16. ^ Кестлер, Артур (1989) 1959. Лунатики. Аркана, Книги о пингвинах.
17. , стр. 194–195
18. ^ Модель деферента / эпицикла фактически используется для вычисления положения Луны, необходимого для определения современных индуистских календарей. См. Нахума Дершовица и Эдварда М. Рейнгольда: Календарные расчеты, Cambridge University Press, 1997, глава 14. (
19. ISBN 0-521-56474-3)
20. ^ Гольдштейн, Бернард Р. (1972). «Теория и наблюдения в средневековой астрономии». Исида. 63 (1): 39–47 40–41. Дои:10.1086/350839.
21. ^ Коллерстрем, Николас (2000). Забытая лунная теория Ньютона. Green Lion Press. ISBN1-888009-08-X .
22. ^ Дороти Стимсон, Постепенное принятие теории Вселенной Коперника. (Нью-Йорк, 1917 г.), п. 14.. Цитата из Джон Милтон с потерянный рай, Книга 8, 11.82–85.
23. ^ Роберт Палтер, Подход к истории ранней астрономии
24. ^ Британская энциклопедия, 1968, т. 2, стр. 645. Это наибольшее число у Оуэна Джинджериха, Альфонсо Икс. Джинджерич также выразила сомнение по поводу цитаты, приписываемой Альфонсо. В Книга, которую никто не читал (стр. 56), однако, Джинджерич рассказывает, что он бросил вызов Британская энциклопедия о количестве эпициклов. Они ответили, что первоначальный автор записи умер, и ее источник не может быть подтвержден.
25. ^ Джинджерич, Книга, которую никто не читал, п. 57
26. ^ Хэнсон, Норвуд Рассел (1 июня 1960 г.). «Математическая сила эпициклической астрономии» (PDF). Исида. 51 (2): 150–158. Дои:10.1086/348869. ISSN0021-1753. JSTOR226846. Получено 21 октября 2011 .
27. ^ См., Например, эта анимация сделанный Кристианом Карманом и Рамиро Серра, который использует 1000 эпициклов, чтобы проследить за персонажем мультфильма Гомер Симпсон; ср. также Кристиана Кармана «Deferentes, epiciclos y adapaciones.» и «La refutabilidad del Sistema de Epiciclos y Deferentes de Ptolomeo».
28. ^ Ср. Дюгем, Пьер (1969). Чтобы спасти явления, написано эссе об идее физической теории от Платона до Галилея.. Чикаго: Издательство Чикагского университета. OCLC681213472.
29. (выдержка ).
30. ^ Джованни Галлавотти: «Квазипериодические движения от Гиппарха до Колмогорова». В: Rendiconti Lincei — Matematica e Applicazioni. Series 9, Band 12, No. 2, 2001, с. 125–152 (PDF; 205 КБ )
31. ^ Лучио Руссо: Забытая революция. Как наука родилась в 300 г. до н.э. и почему ей пришлось возродиться. Спрингер, Берлин. 2004 г.,
32. ISBN 3-540-20068-1, п. 91.
33. ^ Summa Theologica, Я q. 32 а. 1 объявление 2
34. ^ См., Например, Колб, Рокки, Слепые наблюдатели неба, Addison – Wesley, 1996. С. 299 (
35. ISBN 0-201-48992-9)
36. ^ Тумер, Дж. Дж. (1998). Альмагест Птолемея. Издательство Принстонского университета. п. 23. ISBN0-691-00260-6 .