В первой фазе скорость тела уменьшается по мере движения от начала траектории до точки, соответствующей наибольшей высоте подъема. Во второй фазе тело движется вниз, аналогично движению горизонтально брошенного тела.
Тело, брошенное под углом к горизонту: типы траекторий, формулы
Все бросали камни в небо и наблюдали за траекторией их падения. Это самый распространенный пример движения твердого тела в гравитационном поле нашей планеты. В этой статье мы рассмотрим формулы, которые могут быть полезны при решении задач, связанных со свободным движением тела, брошенного под углом к горизонту.
Когда твердое тело приобретает начальную скорость, набирает высоту, а затем падает обратно на землю, считается, что оно движется по параболической траектории. Действительно, решение уравнений для этого типа движения показывает, что линия, описывающая тело в воздухе, является частью эллипса. Однако для практических целей параболический подход достаточно удобен и дает точные результаты.
Вам это будет интересно: Фотоэлектрический эффект. Красная линия фотоэлектрического эффекта. Красная линия красного света.
Примерами движения тела, брошенного под углом к горизонту, являются снаряд, выпущенный из ствола пушки, удар мяча и даже отскакивание камешков на поверхности воды («жабо»), по которому проводятся международные соревнования.
Тип углового движения изучается в баллистике.
Свойства рассматриваемого типа движения
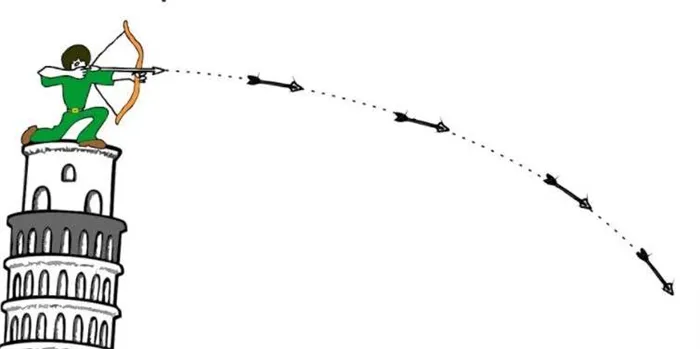
Если рассмотреть траекторию тела, движущегося в поле гравитационного притяжения Земли, то следующие утверждения оказываются верными:
- знание начальной высоты, скорости и угла к горизонту позволяет рассчитать всю траекторию;
- угол вылета равен углу падения тела при условии, что начальная высота равна нулю;
- движение по вертикали можно рассматривать независимо от движения по горизонтали;
Вышеуказанные свойства имеют место, когда сила трения в полете тела пренебрежимо мала. В баллистике при изучении полета ракет учитывается множество различных факторов, включая трение.
Типы параболического движения
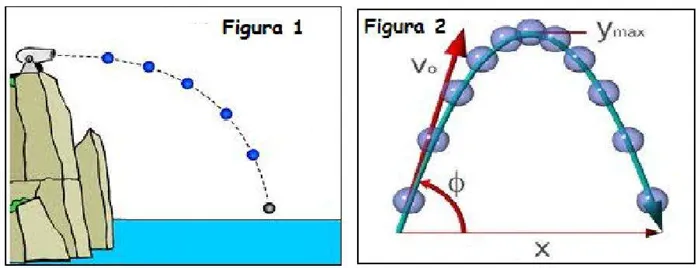
В зависимости от высоты, на которой начинается движение, высоты, на которой оно заканчивается, и направления начальной скорости можно выделить следующие типы параболического движения:
- Полная парабола. В этом случае тело бросают с поверхности земли, и на эту поверхность оно падает, описав при этом полную параболу.
- Половина параболы. Такой график движения тела наблюдается, если его бросить с некоторой высоты h, направив скорость v параллельно горизонту, то есть под углом θ = 0o.
- Часть параболы. Такие траектории возникают, когда тело брошено под некоторым углом θ≠0o, и разница начальной и конечной высоты тоже не равна нулю (h-h0≠0). Большинство траекторий движения объектов относятся именно к этому типу. Например, выстрел с пушки, стоящей на холме, или бросок баскетболистом мяча в корзину.
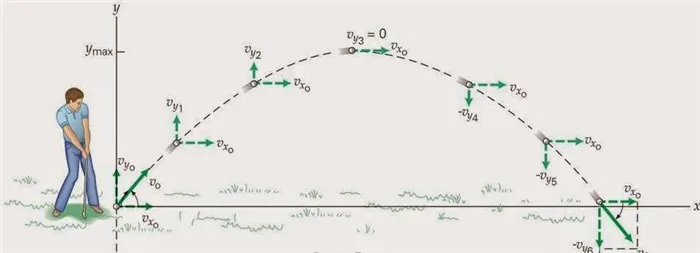
Графическое представление движения тела, соответствующего полной параболе, приведено выше.
Движение тела, брошенного под углом к горизонту
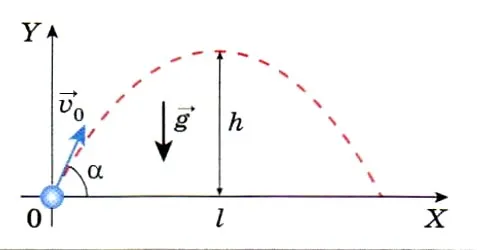
Представьте себе тело, брошенное под углом к горизонту. Пусть сопротивление воздуха будет очень малой величиной, настолько малой, что им можно пренебречь.
Из-за земного притяжения тело поднимается частично над поверхностью и частично под ней. Траектория такого тела представляет собой параболу (рис. 1).
Рис. 1. Парабола – это траектория тела, брошенного под углом к горизонту
Разложим скорость тела
Вместо того чтобы рассматривать сложное движение тела по параболе, мы рассмотрим одновременное и более простое движение двух тел. Одно тело движется вертикально, а второе — горизонтально. Тела начинают и заканчивают движение одновременно.
Мы можем разделить сложное движение на два простых, если разложим скорость тела на проекции. Мы будем рассматривать полученные скорости как скорости отдельно движущихся тел.
Любой вектор, находящийся под углом к осям, может быть разложен на вертикальную и горизонтальную проекции (рис. 2).
Рисунок 2. Вектор начальной скорости тела разлагается на проекции, а затем каждая проекция может быть рассмотрена отдельно
\ \ большой \ упакованный<\beginv_ = v \cdot sin(\alpha) \\ v_ = v \cdot cos(\alpha) \end>\
Вертикальная и горизонтальная проекции скорости
Теперь давайте посмотрим на рисунок 3.
Рисунок 3. Вертикальная часть скорости сначала уменьшается, а затем увеличивается, в то время как горизонтальная часть не меняется.
На этой диаграмме вектор скорости ракеты обозначен черным цветом. Мы видим, что от точки к точке меняется не только сечение, но и направление. То есть свойства вектора меняются.
Вектор, отмеченный на рисунке синим цветом, является горизонтальной проекцией вектора скорости. Понятно, что горизонтальная часть скорости не меняется ни по длине, ни по направлению, т.е. остается постоянной (одинаковой).
Вертикальная проекция скорости отмечена на рисунке красным цветом. Он уменьшается во время восходящего движения и увеличивается во время нисходящего движения.
В высшей точке траектории вертикальная проекция скорости равна нулю. По этой причине скорость в высшей точке направлена только горизонтально и соответствует числу \( v_\). Число \( v_\) является горизонтальной проекцией начальной скорости \( v_\) тела.
Чтобы упростить сложное движение тела в плоскости, мы можем рассмотреть движение двух тел по отдельности: Одно тело движется вертикально с изменением скорости, а другое тело движется горизонтально без изменения скорости.
На рисунке 3 также показано, что
Если тело возвращается в ту плоскость, из которой оно стартовало, то:
- скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет;
- угол \(\alpha\) между скоростью тела на старте и осью Ox будет равен углу между конечной скоростью и горизонталью;
- время подъема равняется времени спуска;
Теперь напишем формулы, описывающие движение тела под углом к горизонту. Давайте разделим движение тела на две части: Восхождение и спуск. Вертикальное движение тела происходит под действием силы тяжести.
Подъем
Когда тело поднимается, оно проходит вертикальное расстояние \(h\):
Вертикальная часть скорости уменьшается — движение равноускоренное:
Горизонтальная часть скорости остается такой же, как и в начале пути.
Поэтому горизонтальное движение вдоль горизонтальной оси равноускоренное, т.е. происходит с постоянной скоростью
Эти формулы можно записать в виде системы:
На максимальной высоте орбиты скорость имеет только горизонтальную проекцию (вертикальной скорости нет, скорость только горизонтальная).
Спуск
По мере опускания тела вертикальная проекция скорости увеличивается — движение изо-ускоряется
По мере опускания тела вертикальное смещение можно определить следующим образом.
Горизонтальная часть скорости остается прежней, она не меняется. Поэтому движение вдоль горизонтальной оси продолжается с постоянной скоростью, и тело преодолевает вторую часть горизонтального расстояния
Объединим эти формулы в систему
После определения времени подъема и спуска мы можем определить общее горизонтальное расстояние:
ВЫСОТА ПОДЪЕМА ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ
По направлению к вершине тело движется одинаково медленно, и его скорость в момент времени t можно определить по формуле ʋ = ʋ0+ Рассмотрим движение тела вдоль оси OU. Получаем, что
Обозначим максимальную высоту тела как h, а время, за которое тело достигает максимальной высоты, как tна. Поскольку в высшей точке траектории ʋy= 0, тогда
Используя уравнение движения тела, получаем
Подставляя выражение (2) в выражение (3), получаем
Если сопротивление воздуха отсутствует, то время tнанеобходимое для подъема тела, равно половине времени, необходимого для движения тела, т.е. равно времени от момента достижения телом максимальной высоты до момента его падения.
ДАЛЬНОСТЬ ПОЛЕТА ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ
Если предположить, что движение вдоль горизонтальной оси равномерное, то расстояние I можно рассчитать по следующей формуле
где t — время полета тела.
С помощью формулы (3) это можно выразить следующим образом:
Если подставить выражение (5) в формулу (4), то получим
Полученное выражение показывает, что для одного и того же значения начальной скорости диапазон зависит от значений проекций ʋ.xи ʋ0xи, следовательно, на величину угла α. В геометрии видно, что максимальное значение l достигается при угле α = 45.
Тарталья первым определил, что наибольшая дальность полета тела, брошенного под углом к горизонту, достигается при угле 45°. Он пришел к этому результату, пытаясь ответить на вопрос артиллериста о том, под каким углом следует располагать ствол пушки, чтобы получить максимально возможную дальность полета пушечного ядра.
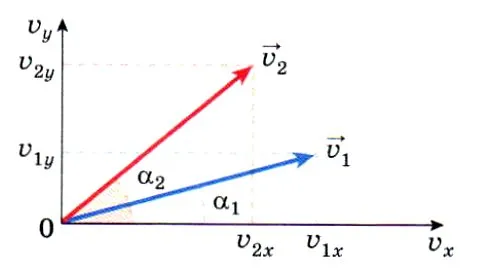
Для одного и того же значения начальной скорости угол ayтем больше, чем больше угол a. По мере увеличения угла a значение проекции ʋxуменьшается.
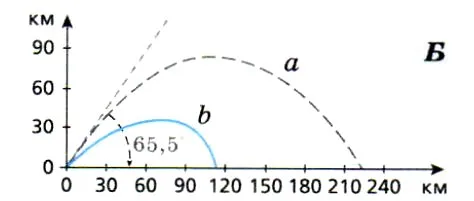
Предполагалось, что траектория пули состоит из двух прямых участков и одного изогнутого участка. Это неудивительно, потому что в реальной жизни траектория такого движения с учетом сопротивления воздуха уже не является параболой, а выглядит как непрерывная линия, показанная на рисунке.
Никколо Тарталья (1500-1557) В своей первой работе «Nuova scienza» (1537) он впервые рассмотрел вопрос о траектории полета запущенного снаряда.
Вы видели конспект по физике за 9 класс: Движение тела, брошенного под углом к горизонту.
Примеры задач с решением
Задание. Во сколько раз изменится время полета тела, брошенного с высоты $h$ в горизонтальном направлении, если скорость тела увеличить в $n$ раз?
Решение. Найдите формулу для расчета времени полета тела при его горизонтальном запуске (рис. 2).
Используйте выражение для равноускоренного движения тела в гравитационном поле в качестве основы для решения задачи:
Используя рис. 2, напишите проекции уравнения (1.1) на координатные оси:
Поскольку тело падает на землю $y=0,$, этот факт и второе уравнение системы (1.2) дают время полета:
Как видим, время полета тела не зависит от его начальной скорости, т.е. если начальную скорость увеличить в $n$ раз, то время полета тела не изменится.
Реакция. Она не меняется.
Задание. Если начальную скорость тела увеличить в $n$ раз, то как изменится расстояние тела в предыдущей задаче?
Решение. Дальность — это расстояние, которое проходит тело вдоль горизонтальной оси. Это означает, что нам необходимо уравнение:
из системы (1.2) в первом примере. Подставив вместо $t,$ время полета, найденное в (1.3), мы получим дальность полета ($s_$):
Из формулы (2.2) видно, что при данных условиях движения дальность прямо пропорциональна скорости броска тела, т.е. во сколько раз увеличивается начальная скорость, во столько раз увеличивается дальность броска тела.
Реакция. Радиус действия тела увеличивается в $n$ раз.

Проверенные писатели готовы помочь в написании работ любой сложности
Мы уже помогли 4 396 студентам и школьникам выполнить задание от решения задачи до магистерской диссертации с отличием! Узнайте стоимость вашего задания за 15 минут!
Вопросы:
1. приведите примеры движения тела, брошенного под углом к горизонту.
2. какова траектория тела, брошенного под углом к горизонту?
3. запишите выражения для определения:
(a) Время полета,
б) дальность полета,
c) максимальная высота подъема тела, брошенного под углом к горизонту.
4. Какие выводы можно сделать из анализа рисунка 2.44, б?
Пример решения задачи
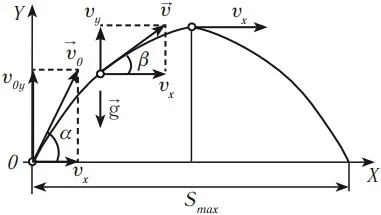
Под каким углом к горизонту нужно бросить тело, чтобы максимальная высота его подъема была вдвое больше максимальной дальности полета (рис. 2.45)? Сопротивлением воздуха следует пренебречь. 1.
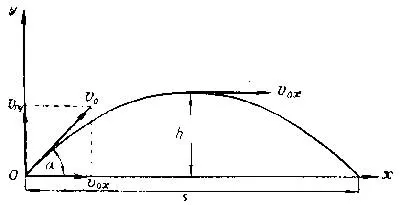
Упражнения:
1. с какой высоты был брошен мяч в горизонтальном направлении со скоростью 10 м/с, если он упал на расстоянии 4,9 м от точки бросания? Игнорируйте сопротивление воздуха.
2. камень брошен с горы в горизонтальном направлении со скоростью 15 м/с. Сколько времени потребуется, чтобы его скорость была под углом 45° к горизонту? Игнорируйте сопротивление воздуха.
3 Мяч брошен под углом 30° к горизонту с начальной скоростью 10 м/с.
Определите:
(a) Проекции u0x(а) (4) (а) (а) (а) и (б) (у) (а) (4))0yначальной скорости,
(b) высота подъема,
(d) Амплитуда сферы. Игнорируйте сопротивление воздуха.
4. Двое детей играют с мячом, перебрасывая его друг другу. Какой максимальной высоты достигает мяч во время игры, когда он летит от одного игрока к другому в течение 2 секунд? Игнорируйте сопротивление ветра.
Программный код поставленной задачи
Для успешного моделирования движения объекта необходимо учитывать гравитацию и сопротивление воздуха. Если пренебречь сопротивлением воздуха, то единственной силой, действующей на тело в полете, является сила тяжести. Согласно 2-му закону Ньютона, объект движется с ускорением, соответствующим ускорению, обусловленному гравитацией.
Любое движение материальной точки может быть представлено как суперпозиция независимых движений вдоль координатных осей. Определим начальные условия.
Полный код программы для всех рассмотренных соотношений движения можно найти в Приложении А.
Определим начальные условия (таблица 1).
Таблица 1: Начальные условия








