и является вектором, перпендикулярным Ω и r ( t ), направленным по касательной к орбите и имеющим значение ω R. Аналогично, ускорение определяется как:
Движение по окружности. Центростремительное и тангенциальное ускорения
Нас постоянно окружает круговое движение — будь то мотоциклист на мототреке, вращение груза на веревке, движение по изогнутому круговому мосту, любой поворот на дороге также можно рассматривать как движение по части круга и т.д.
Представим, что мы смотрим на мотоциклетный трек сверху (см. рис. 1). Пусть в точке \(A\) находится мотоциклист, движущийся с постоянной линейной скоростью \(\vec\), и за определенное время \(t\) он движется по дуге окружности \(^\) к точке \(^\). Пройденное расстояние равно длине дуги \(^\).
Определение Линейная скорость — это расстояние, пройденное мотоциклистом за единицу времени (например, за одну секунду):
Очевидно, что чем большее расстояние (больше длина дуги) тело может пройти за то же время, тем больше его линейная скорость и тем быстрее оно движется. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда указывает на касательную к траектории, в данном случае на касательную к окружности. Это пригодится позже.
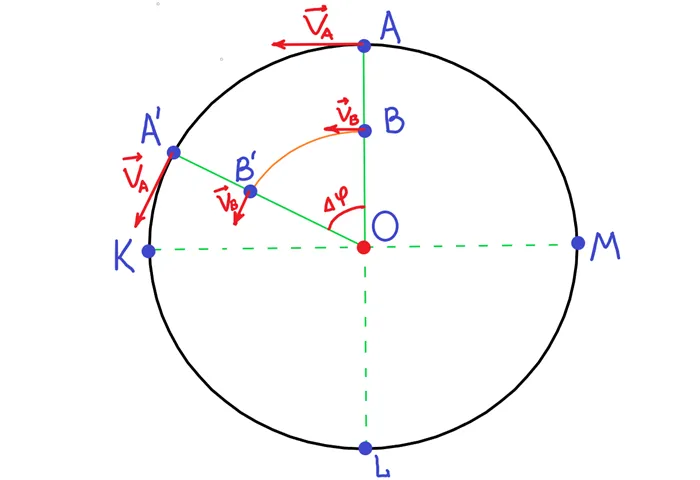
Рисунок 1: Линейная скорость для вращательного движения. Угловая скорость.
Поэтому при круговом движении мы можем измерять скорость двумя способами: линейная скорость (сколько расстояние проходит тело за единицу времени) и угловая скорость (на сколько углов поворачивается тело за единицу времени). Эти скорости, конечно, должны быть связаны друг с другом.
Но прежде чем вывести это соотношение, представим, что отрезок \(AO\) вращается по окружности (см. рисунок 1) и в момент времени \(t\) проходит через отрезок \(^O\) — точка \(A\) проходит через точку \(^\) и точка \(B\) проходит через точку \(^\).
Таким образом, точка \(A\) покрывает длину дуги \(^\) для \(t\), а точка \(B\) покрывает то же расстояние \(^\) (обе точки лежат на одной прямой) для \(^\).
И на какой угол могут повернуться точки \(A\) и \(B\) за то же время \(t\)?
На рисунке 1 показано, что они оба вращаются на один и тот же угол \(\Дельта\варфи\). А поскольку угловая скорость по определению является отношением угла ко времени, то угловые скорости точек \(A\) и \(B\) равны.
Таким образом, линейная скорость увеличивается с расстоянием, а угловая скорость не меняется. Тогда кажется логичным использовать следующую формулу для связи угловой и линейной скоростей:
Где \(V\) — линейная скорость,
\(\omega\) — угловая скорость,
\(R\) — радиус инерции.
Период и частота вращения
Частота и период являются важными характеристиками любого вращательного движения:
Определение Период — это время, которое требуется телу, чтобы совершить один полный оборот.
В нашем примере с мотоциклистом период — это время, которое требуется мотоциклисту для завершения одного полного цикла.
Из геометрии мы знаем, что длина дуги может быть вычислена как \(2*\pi*R\), где \(R\) — радиус окружности. В случае равномерного движения период можно вычислить, разделив расстояние на скорость: $T=\frac<2*\pi*R>Подставляя в формулу \((1)\) для линейной скорости угловую скорость: $T=\frac<2*\pi><\omega>Где \(V\) — линейная угловая скорость.
В системе СИ период измеряется в \(^\).
Определение Частота — это количество оборотов в единицу времени.
В случае мотоциклиста частота — это количество кругов, которые он делает, например, за час. Частота обычно измеряется в оборотах в секунду.
Период и частота вращения связаны выражением: $T=\frac;$. Отсюда можно получить формулы для частоты, подставив период: $<2*\pi*R>u=\frac<\omega><2*\pi>;$
= {\frac
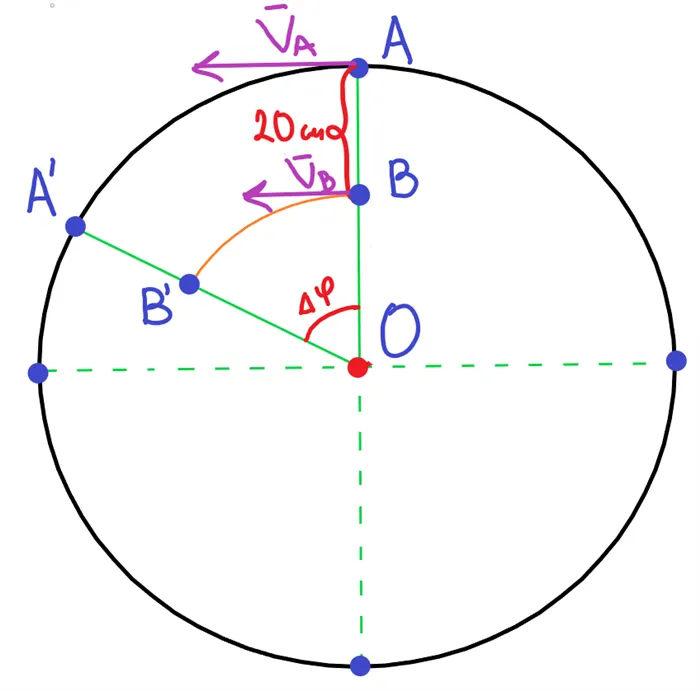
Скорость точки на краю вращающегося диска равна \(V_A=15(м/с)\), а скорость точки, находящейся на 0,2 (м) ближе к центру вращения, равна \(V_B=10(м/с)\). Определите частоту вращения и радиус диска.
Решение. Поскольку обе точки находятся на одном радиусе, они имеют одинаковые угловые скорости. Запишите угловые скорости точек \(A\) и \(B\) и установите их равенство: $\omega_A=\frac;$\omega_B=\frac;$\omega_A=\omega_B;$\frac=\frac;$ Из условия \(A0=BO+0. 2\): $\frac=\frac;$$\frac=\frac;$$ $15*BO=(BO+0. 2)*10;$5*BO=2;$BO=0.4.$ Мы нашли радиус окружности, на которой вращается точка \(B\), тогда радиус точки \(A\) больше, чем \(0.2(м)\) — \(0.6(м)\).<2*\pi*R_A>Для определения частоты используем формулу: $
Центростремительное (нормальное) ускорение
u=\frac
=\frac=3.98(об/сек);$ ответ: \(R=0.6(м)\) и \(
u=3.98(об/сек)\).
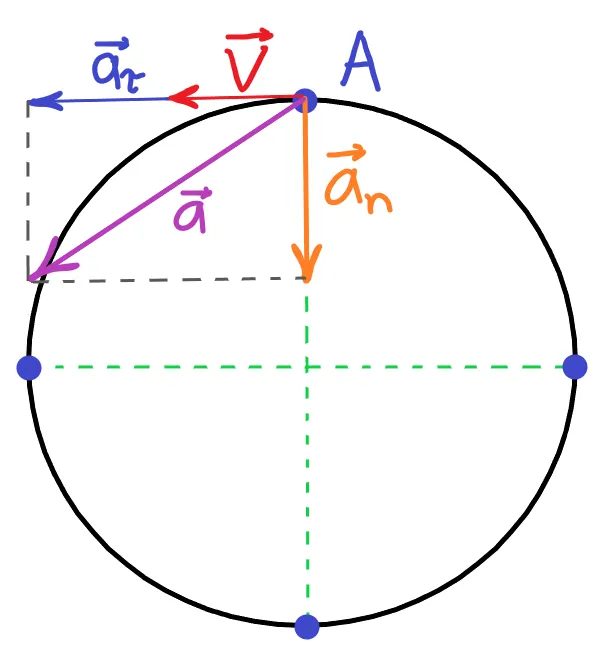
Давайте вернемся к нашему примеру с мотоциклистом, едущим по круговому мототреку. (См. Рисунок 3) Сначала предположим, что линейная скорость мотоциклиста постоянна, т.е. он движется плавно, что означает, что его ускорение должно быть равно нулю. Это верно, но при движении по кругу (или другой криволинейной траектории), даже при постоянной скорости, возникает новый тип ускорения — центростремительное ускорение, которое также называют «нормальным» ускорением. Она возникает из-за изменения направления вектора скорости.
Угловой путь
На самом деле, для решения задач не обязательно понимать природу центростремительного ускорения. Достаточно знать, что любое искривленное движение создает это ускорение. Его можно рассчитать по формуле,
{\(R\) — радиус окружности.
Приведем линейную скорость в терминах угловой скорости, \(V=\omega*R\). И у нас есть еще одна формула для центростремительного ускорения: $a_n=\omega^2*R;$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.
Во-первых, помните, что линейное перемещение — это разница между конечным и начальным положением точки на оси (рис. 1).
Рис. 1. Линейное перемещение — это разница между начальным и конечным положением точки на оси.
Теперь рассмотрим колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отмечаем красную точку, от которой измеряем углы. Предположим, что нулевая точка находится вблизи этой точки.
Рисунок 2: Точка перемещается из положения 1 в положение 2, пройдя угловое расстояние.
Выберем точку на ободе, например, сосок. Первоначально сосок находился в точке 1. Точка 1 смещена на угол \(\gamma_\) от начала координат.
Повернем колесо в направлении, указанном синей стрелкой. Повернем колесо на определенный угол так, чтобы ниппель в конце движения переместился в точку, обозначенную на рисунке цифрой 2. Эта точка смещена на угол \(\gamma_\) относительно начала координат.
Угловая скорость — куда она направлена
По аналогии с поступательным движением, угловое расстояние, пройденное соском, равно разнице между угловыми положениями точек 1 и 2.
\(v \left( \frac>\(\varphi \left( \text
ight)\) — угловое смещение, измеряемое в радианах.
\(\omega \left( \frac>Угловое смещение — это угол, на который поворачивается сосок по отношению к своему исходному положению.
Если тело движется равномерно (с постоянной скоростью), линейная скорость может быть определена по следующей формуле
ight)\) — Линейная скорость — это расстояние, деленное на время, поэтому она измеряется в метрах, деленных на секунды.<\omega>Как и в линейном случае, угловая скорость получается путем деления углового расстояния на время движения.
<\omega>ight)\) — Угловая скорость — это угловое расстояние, деленное на время, поэтому она измеряется в радианах, деленных на секунды.
Угловая скорость \( \omega\) является вектором, как и линейная скорость. Но в отличие от линейной скорости, ее направление можно определить по правилу винта.
Примечание: Направление вектора угловой скорости \( \vec
\) можно определить по правилу Боракса (правый винт)!
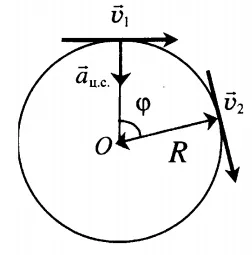
На рисунке 3 круг находится в горизонтальной плоскости, а вектор \( \vec \vec
Связь между линейной и угловой скоростью
\) выравнивается вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.
Рисунок 3. Линейная и угловая скорость точки, вращающейся по окружности. Угловая скорость выравнивается вдоль оси вращения в соответствии с правилом правого винта.
При движении по окружности вектор линейной скорости \(\vec\) меняет направление. Но в любой точке окружности вектор \(\vec\) является касательной к окружности, т.е. перпендикуляром к радиусу.
\(\omega \left( \frac>Примечание: Касательная и радиус перпендикулярны друг другу, как известно из геометрии.
\(v \left( \frac>Если точка начинает вращаться в противоположном направлении, векторы линейной и угловой скорости вращаются в направлениях, противоположных направлениям, показанным на рисунке 3.
Угловая скорость и линейная скорость математически связаны между собой. Линейная скорость — это векторное произведение вектора угловой скорости и радиус-вектора окружности.
Вращение Земли
Примечания: Радиус круга — это вектор, направленный из центра круга к его внешней границе.
Скалярная форма обозначения отношения скоростей:
Движение по циклоиде*
ight)\) — угловая скорость,
ight)\) — линейная скорость,








