Многие пары сил, действующих на тело в плоскости, можно заменить одной парой сил (изодинамической парой), момент которой равен алгебраической сумме моментов этих пар:
Момент силы
В физике момент силы — это векторная величина, равная векторному произведению радиус-вектора, заданного осью вращения в точке приложения силы, и ее направления.
Категория описывает действие силы по отношению к твердому телу.
Бывает, что велосипедисту приходится поворачивать руль транспортного средства вручную. Это намного быстрее, чем захват спиц, так как они находятся ближе к точке поворота. Тяговое усилие — это крутящий момент, т.е. вращательное движение.
Осторожно. Если учитель обнаружит плагиат в вашей работе, у вас будут большие неприятности (вплоть до исключения из школы). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Крутящий момент и угловой момент не идентичны, поскольку термин «угловой момент» относится к внешней силе, действующей на объект, а термин «угловой момент» относится к внутренней силе, действующей на объект под действием нагрузки.
В физике крутящий момент интерпретируется как вращение.
В теории эта категория также называется импульсом пары сил, термин, восходящий к работе Архимеда о рычагах. Так, если на рычаг перпендикулярно действует сила, то импульс силы получается умножением величины силы на расстояние от оси вращения рычага.
В линейной механике сила — это мера способности придать телу линейное ускорение. Аналогично, крутящий момент точки — это мера способности придать системе угловое ускорение. Она также накладывает угловое ускорение — эти два параметра прямо пропорциональны друг другу.
Например, если отодвинуть дверь дальше от дверных петель, то есть туда, где находится ручка, она открывается легче и быстрее. Отсюда видна разница во вращении/вращательной способности. Другой пример. Тяжелый предмет легче удержать, если прижать к нему руку, а не держать ее на вытянутой руке. Таким образом, в приведенных выше случаях импульс силы изменяется по мере уменьшения/увеличения рычага.
Формула для импульса выглядит следующим образом:
M — это импульс силы (также обозначается как t), а dL — изменение импульса за бесконечно малый промежуток времени dt.
Абсолютная величина момента силы
Абсолютное значение импульса силы — это величина, равная произведению абсолютного значения на плечо данной силы относительно выбранной точки.
Рассмотрим следующий рисунок.
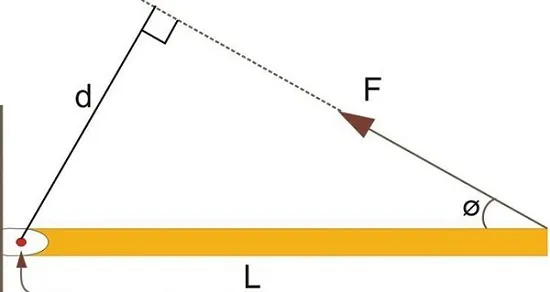
На нем изображен стержень длиной L. Таким образом, одним концом он прикреплен к вертикальной плоскости с помощью шарнира, а другой конец свободен. F¯ действует на него. Угол между стержнем и вектором равен φ. Угловой момент должен определяться векторным произведением. Его мера равна произведению: абсолютных значений, умноженных на синус угла между ними.
Используя формулы из тригонометрии, мы можем составить следующее уравнение:
Возвращаясь к рисунку, перепишем равенство в виде:
Здесь \(d = L*sin(φ)\) — величина, соответствующая расстоянию от вектора силы до оси вращения. F образует больший крутящий момент при большем d.
Работа момента силы
Крутящий момент рассчитывается в ньютонах на метр, т.е. имеет ту же размерность, что и работа и энергия в естественных науках. Однако следует отметить, что это понятие является векторной величиной, которую нельзя рассматривать как работу. Импульс силы совершает работу в соответствии с формулой:
Значение θ указывает центральный угол в радианах, вокруг которого вращается система в данный момент времени t.
Момент силы относительно точки
Момент силы относительно точки (или центра) является вращательным эффектом силы и описывает вращение твердого тела вокруг точки под действием действующей силы.
Момент силы относительно точки (рис. 1.1) равен векторному произведению радиус-вектора точки приложения силы и вектора силы.
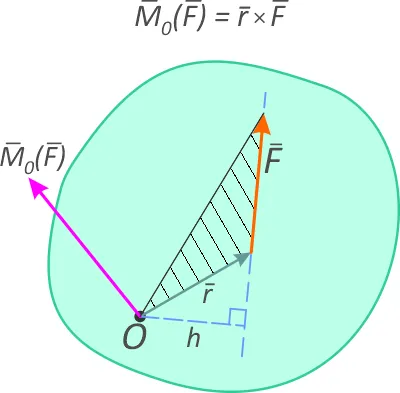
Вектор момента перпендикулярен плоскости, в которой расположены сила и точка, в направлении, из которого следует, что вращение происходит против часовой стрелки из-за приложения силы.
Вычисление момента
Вектор крутящего момента характеризует положение плоскости и направление вращательного действия силы и дает меру этого действия:
Где h — плечо силы (кратчайшее расстояние от точки O — центра крутящего момента — до линии действия силы). Когда сила проходит через точку, ее импульс относительно этой точки равен нулю.
Импульс силы относительно точки не меняется, когда сила движется вдоль линии действия.
Если силы лежат в одной плоскости, то используется понятие алгебраического момента силы.
Алгебраический момент силы относительно точки (или центра) равен произведению коэффициента силы на плечо со знаком (рис. 1.2).
Наш короткий видеоурок о крутящем моменте с примерами:
Правило знаков
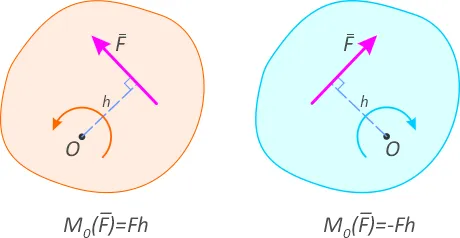
Если сила F задана своими проекциями на координатные оси Fx, Fy, Fzи заданы координаты x, y и z точки приложения силы, момент силы относительно начала координат вычисляется следующим образом:
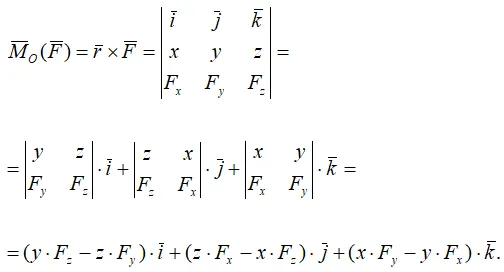
Проекции моментов сил на координатные оси равны:

Уважаемые студенты. На нашем сайте вы найдете помощь по техническим и другим вопросам: ✔ Решение задач и тестов ✔ Научные работы ✔ Помощь на экзаменах.
Предыстория
Строго говоря, вектор, обозначающий момент силы, введен искусственно, потому что он удобен для вычисления работы, совершенной на изогнутом участке относительно неподвижной оси, и для вычисления общего момента силы всей системы, так как его можно суммировать. Чтобы понять, откуда взялось обозначение импульса и как оно появилось, стоит рассмотреть действие силы на рычаг, вращающийся вокруг неподвижной оси.
Работа, совершаемая под действием силы вокруг неподвижной оси, может быть рассчитана на основе следующих соображений.
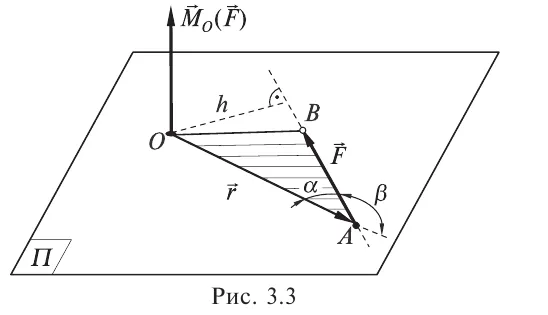
Пусть под действием силы конец рычага пройдет бесконечное расстояние. Обозначим равенством вектор и вектор силы.
Поэтому бесконечно малая работа в бесконечно малой части и вектор силы, т.е.
Теперь попробуем выразить коэффициент вектора, и проекцию вектора силы
Так как для бесконечно малого перемещения рычага, используя соотношения для прямоугольного треугольника, можно записать следующее равенство:, где в случае малого угла справедливо и следовательно \right| d\varphi» width=»» height=»» />
Для проекции вектора силы, видно, что угол » width=»» height=»» />, а так как \right )>= \sin» width=»» height=»» />, получаем, что = \left| \vec \right| \sin» width=»» height=»» />.
Теперь запишем бесконечно малую работу через новые равенства \right| \sin» width=»» height=»» />или<\left (\alpha \right )>d\varphi» width=»» height=»» />.
ight| \sin<\left (\alpha \right )>» width=»» height=»» />Теперь мы видим, что произведение
ight| \sin
Единицы
это не что иное, как мера векторного произведения векторов, то есть мера вектора силы-крутящего момента.
,
Теперь вся работа написана очень просто: …
Специальные случаи
Формула момента рычага
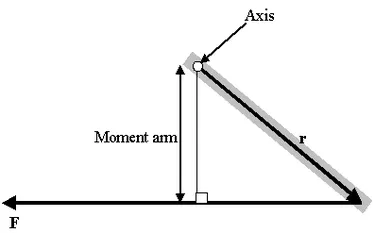
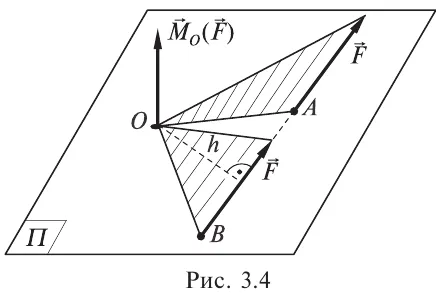
Момент силы — это сила на расстояние, и в системе СИ единицей измерения момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, также определяется как 1 Н-м, но эта единица не используется для импульса силы. Когда энергия представлена как результат «сила, умноженная на перемещение», энергия является скалярной, тогда как момент силы — это «сила, умноженная на векторное перемещение» и, таким образом, является (псевдо) векторной величиной. Конечно, совпадение размеров этих величин не случайно; крутящий момент в 1 Н-м, действующий на целый оборот, требует энергии всего в 2*p-джоулей. Математика
Где E — энергия, M — крутящий момент, а θ — угол в радианах.
Очень интересный частный случай представлен в виде определения импульса силы в поле:
= КРУТЯЩИЙ МОМЕНТ РЫЧАГА * СИЛА
Сила под углом
Проблема с этим представлением заключается в том, что оно не дает направления импульса силы, только его величину, поэтому трудно учесть величину в трехмерном случае. Если сила перпендикулярна вектору r, то импульс рычага равен расстоянию от центра, а импульс силы максимален
Статическое равновесие
= РАССТОЯНИЕ_ОТ_ЦЕНТРА * СИЛА
Момент силы как функция от времени
\over dt>\,\!» width=»» height=»» />,
Если сила F направлена на рычаг r под углом θ, то M = r*F*sinθ, где θ — угол между рычагом и приложенной силой.
\,\!» width=»» height=»» />,
Для того чтобы объект находился в равновесии, необходимо, чтобы не только сумма всех сил была равна нулю, но и сумма всех моментов сил относительно любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях SH = 0, SV = 0 и момент силы в третьем измерении SM = 0.
\over dt>=I\boldsymbol \,\!» width=»» height=»» />,
где L — импульс. Импульс твердого тела можно описать произведением момента инерции и угловой скорости.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных См. также
- Момент импульса
- раздела Википедии на русском языке. Оригинальная статья находится по адресу: Момент силы. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .








