Векторное произведение векторов. Векторное произведение векторов формула.

В разных источниках в вашей голове будет множество различных характеристик смешанного проекта. С практической точки зрения, я думаю, важно отметить несколько моментов:

Векторное произведение

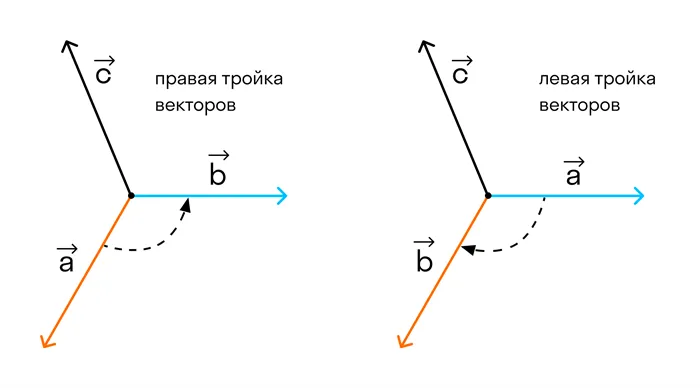
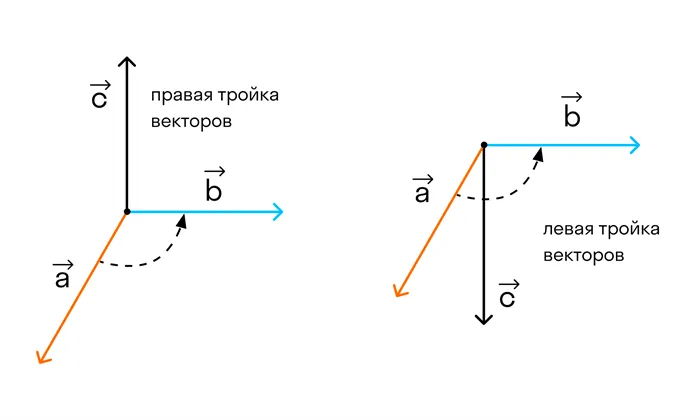
Три вектора называются упорядоченным триплетом, если указано, какой из этих векторов первый, какой второй и какой третий.

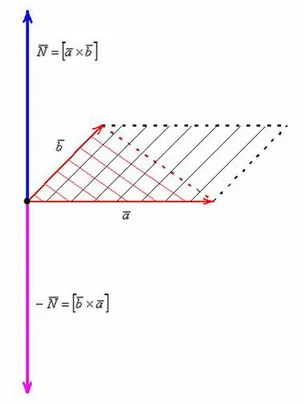
Триада некривых векторов abc называется правой (левой), если эти векторы расположены по общему принципу так, как могут быть расположены большой, некривой указательный и средний пальцы правой (левой) руки.

Определение

Векторным произведением вектора a на вектор b называется вектор c, обозначаемый =\left>\right>» width=»» height=»» />и отвечать следующим требованиям:

• длина вектора c равна произведению длин векторов a и b на синусугла φ; между ними

\right|=\left|\right|\left|>\right|\sin \phi>» width=»» height=»» />

• вектор c ортогонален каждому из векторов a и b
• вектор c направлен так, что тройка векторов abc является правой.

Геометрические свойства векторного произведения

• Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
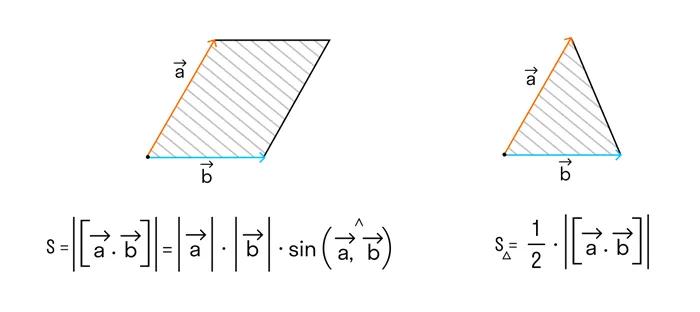
• Модуль векторного произведения ab равняется площади S орт векторного произведения a и b, а S — площадь параллелограмма, построенного на приведённых к общему началу векторах a и b, то для векторного произведения справедлива формула:

>=S>>» width=»» height=»» />

• Если c — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, e — единичный вектор, лежащий в плоскости π и ортогональный к c, g — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула

>\right=Pr_>\left|>\right|>>» width=»» height=»» />

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a =x; a_y; a_z>и b = bx; b_y; b_z>в декартовой системе координат является вектором, значение которого можно вычислить по следующим формулам

a × b = i j k a_xa_ya_zb_xb_yb_z= i ( a_yb_z— a_zb_y) — j ( a_xb_z— a_zb_x) + k ( a_xb_y— a_yb_x)

Свойства векторного произведения векторов

Коэффициент векторного произведения двух векторов a и b равен площади параллелограмма, построенного из этих векторов:

Площадь треугольника, образованного из векторов a и b, равна половине коэффициента векторного произведения этих векторов:

Векторное произведение двух ненулевых векторов a и b равно нулю только в том случае, если векторы коллинеарны.

Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.

Примеры задач на вычисления векторного произведения векторов

Пример 1: Найдите векторное произведение векторов a = n = n. Найдите векторное произведение векторов a = n = n.<1; 2; 3>и b = .

= i (-4 — 3) — j (-2 — 6) + k (1 — 4) = -7 i + 8 j — 3 k = .

Пример 2. Найдите площадь треугольника, образованного векторами a = .<-1; 2; -2>и b = .

Решение:

= i (-2 + 2) — j (1 + 4) + k (-1 — 4) = -5 j — 5 k =

Из свойств векторного произведения:

SD = 1 2 | a × b | = 1 2 √ 0 2 + 5 2 + 5 2 = 1 2 √ 25 + 25 = 1 2 √ 50 = 5√ 2 = 2,5√ 2

Реакция.

Векторное произведение векторов. Смешанное произведение векторов

В этом уроке мы рассмотрим еще две операции с векторами: Векторное произведение векторов и смешанное произведение векторов (для тех, кому это нужно, следует ссылка). Неважно, иногда для счастья нам нужно больше, чем скалярно-векторное произведение. Это векторная зависимость. Может сложиться впечатление, что мы входим в лабиринт аналитической геометрии. Это не так. В этой части высшей математики не так много дерева, достаточно для Пиноккио. На самом деле, материал очень обычный и простой — едва ли сложнее самого скалярного произведения, и формальных проблем тоже будет меньше. Главное в аналитической геометрии, как многие убеждены или были убеждены, это то, что вы не допускаете НИКАКИХ ошибок в своих вычислениях. Повторяйте эту поговорку, и вы будете счастливы =)

Если векторы мелькают где-то вдалеке, как молния на горизонте, не волнуйтесь, начните с курса «Векторы для чайников», чтобы восстановить или заново освоить базовые знания о векторах. Хотя опытные читатели могут читать информацию выборочно, я постарался собрать как можно более полную коллекцию примеров, которые часто встречаются в практических приложениях.

Чем я могу поделиться с вами прямо сейчас? Когда я был ребенком, я мог жонглировать двумя или даже тремя мячами. Он стал искусным. Теперь вам не нужно жонглировать, потому что мы рассматриваем только пространственные векторы, а плоские векторы с двумя координатами опускаем. Почему? Вот как появились эти операции — вектор и смешанное произведение векторов определены и работают в трехмерном пространстве. Уже легче!

Примеры решения задач

Пример 1

α) Найдите длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

b) Найдите площадь параллелограмма, построенного с помощью векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

α) По условию, нам нужно найти длину векторного произведения. Введите данные в формулу:

Поскольку в задаче речь идет о длине, ответ дается в единицах.

б) Задача заключается в определении площади параллелограмма, образованного векторами →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найдите |-3→a x 2→b|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию, нам все равно нужно найти длину векторного произведения. Давайте применим нашу формулу:

Согласно корреляционным законам, мы выводим константу за пределы векторного произведения.

Мы переносим константу на модуль, а модуль позволяет нам убрать знак минус. Длина не может быть отрицательной.

Пример 3

Найдите площадь треугольника A (0, 2, 0), B (-2, 5, 0), C (-2, 2, 6) с вершинами.

Сначала найдите векторы:

Тогда векторное произведение:

Вычислите его длину:

Подставьте полученные данные в формулы для площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

По определению, длина векторного произведения векторов равна

А из уроков геометрии в школе мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, сторонами которого являются векторы →a и →b, если смотреть из одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами →a и →b и углом между ними, равным (→a, →b). В этом заключается геометрический смысл векторного произведения.

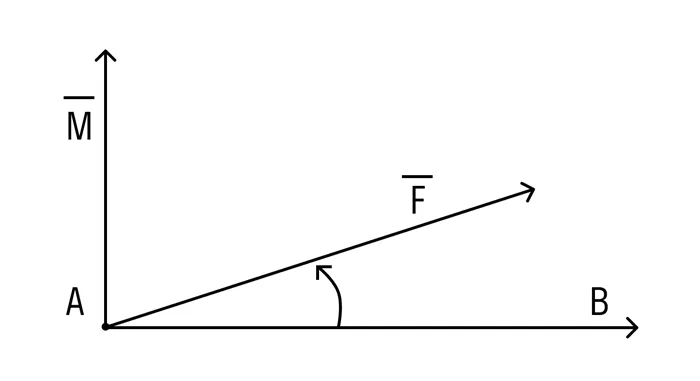
Физический смысл векторного произведения

В механике, отрасли физики, векторное произведение можно использовать для определения импульса силы относительно точки в пространстве. Поэтому давайте сформулируем еще одно важное определение.

Под термином импульс силы →F, действующей на точку B относительно точки A, мы понимаем следующее векторное произведение →A B × →F.

Вектор линейной скорости →V точки колеса M равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, т.е. →V = →W`→rM.

Смешанное произведение векторов

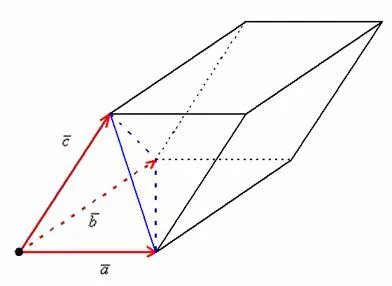
Определение. Когда вектор умножается векторно на вектор и полученный вектор затем умножается скалярно на вектор, полученное число называется смешанным произведением векторов, и.

Геометрический смысл смешанного произведения

Теорема 3: Смешанное произведение равно объему параллелепипеда, образованного векторами, и, со знаком плюс, если тройка идет по часовой стрелке, и со знаком минус, если против часовой. Когда, и совпадают, они равны нулю.

Следствие 1. Равенство .

Следствие 2. Необходимым и достаточным условием конгруэнтности трех векторов является то, что их смешанное произведение равно нулю.

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Выражение смешанного произведения в декартовых координатах

Теорема 4: Если три вектора, и определяются своими декартовыми координатами.

то смешанное произведение дается координатами трех квадратов двух квадратичных прямых.

равен определителю, каждая строка которого равна координатам перемножаемых векторов, т.е.

Пример 6. заданные векторы:

1) смешанное произведение векторов,

2) объем параллелепипеда, образованного данными векторами,

3) объем треугольной пирамиды на основе трех заданных векторов.

Из этого следует. Необходимым и достаточным условием сложности трех векторов, и является равенство определителя, строки которого являются координатами этих векторов, нулю, т.е. равенство