Для описания функционирования различных электронных устройств имеет смысл использовать элементы логической алгебры, которая, как известно, работает с переменными, принимающими только два значения 1 и 0, то есть включено или выключено.
Логика. Основные сведения.
Высказывания (или также: высказывания) об объектах в мире строятся из элементарных высказываний. Такие утверждения говорят что-то о свойствах объекта или об отношениях между объектами (обычно между двумя объектами).
- Забор красный. Здесь забор – объект, а красный описывает его свойство. «красный» (иногда говорят – свойство «быть красным»). Имеется в виду конкретный забор, а не забор вообще! В русском языке свойства часто (но не всегда) выражаются прилагательными.
- Коля и Петя – друзья. Здесь Коля и Петя – «объекты», а слово друзья описывает отношение между ними. Это отношение симметрично – смысл сказанного не поменяется, если написать «Петя и Коля – друзья». Здесь, как и во всех элементарных высказываниях, имеются в виду конкретные люди.
- Коля старше, чем Петя. Здесь отношение описывается словами «старше, чем». Это отношение не является симметричным.
Утверждение может быть истинным (true) или ложным (false). Например, Коля может быть больше Пети (тогда верно утверждение 3). Но может быть и так, что Коля младше Петра, или что они одного возраста. Тогда утверждение ложно.
1.2 Объекты, свойства и отношения в математике.
В математике мы имеем дело с математическими объектами, их свойствами и отношениями. Примеры математических объектов: Числа: натуральные числа, целые числа, логические числа (или обыкновенные дроби), действительные числа; точки, линии, множества. На уроках математики вы познакомились с числами, точками и линиями. Вы можете прочитать немного о наборах здесь.
Вот примеры свойств, отношений и утверждений для целых чисел (где описываются свойства и отношения, вместо чисел есть точки…) .
Свойства: … ровный, … нечетное, … является положительным.
Примеры утверждений: (1) 4 — четное число. (2) 4 нечетно. (3) 4 является положительным. Здесь первое и третье утверждения истинны, а второе — ложно.
Отношения: … больше, чем …- … меньше, чем …- … делится на … .
Примеры высказываний. Опять же, первое и третье утверждения истинны, а второе — ложно.
В математике отношения часто представляются с помощью специальных символов. Например, 6<3.
Примечание. Вместо «явного» указания чисел в операторах, например, можно также использовать выражения, значениями которых являются числа. Пример:
1.3 Общие положения.
В школьной математике (и не только в ней 🙂 ) в элементарных высказываниях часто используются не только «имена» объектов (чисел, величин и т.д.), но и переменные. Пример:
a + b = b + a
Под этим подразумевается следующее. Если заменить любое число на числа a и b, то получится истинное высказывание. Это означает, что все следующие утверждения верны, и бесконечно много других, подобных им:
27 + 12 = 12 + 27 (замените a на 27 и b на 12).
2 + 5 = 5 + 2 (замените a на 2 и b на 5)
5 + 2 = 2 + 5 (замените a на 5 и b на 2)
5 + 5 = 5 + 5 (замените a на 5 и b на 5).
2. Логические значения, логические связки и логические высказывания
2.1 Сложные заявления
Вы можете использовать AND, OR, NOT для построения более сложных (составных) высказываний из элементарных высказываний.
Примеры. Забор красного цвета И забор сделан из дерева.
Коля старше Пети ИЛИ Коля старше Феди.
Забор НЕ красный.
Смысл этих высказываний очевиден.
Оператор AND содержит два элементарных оператора. Составное высказывание с И истинно тогда и только тогда, когда истинны эти два элементарных высказывания. Если хотя бы одно из них ложно, то составное высказывание ложно.
Высказывание с OR также содержит два элементарных высказывания. Составное высказывание с ИЛИ истинно тогда и только тогда, когда истинно хотя бы одно из этих элементарных высказываний. Если оба ложны, то составное высказывание ложно.
Высказывание с NOT содержит элементарное высказывание (в русском языке NOT часто находится в середине этого высказывания). Составное высказывание с NOT истинно, если исходное элементарное высказывание ложно, и наоборот, если исходное высказывание истинно, то составное высказывание с NOT ложно.
Составные высказывания могут быть образованы не только из элементарных высказываний, но и из других составных высказываний. Построение составных высказываний аналогично построению алгебраических выражений. Например, понятно, что означает следующее утверждение (хотя оно написано не по-русски, а в скобках : )
(Коля старше Пети ИЛИ Коля старше Феди) И (Коля НЕ старше Вани).
Существует 3 элементарных утверждения.
2.2 Соответствующие значения. Логические операции.
Мы уже узнали, что любое высказывание может принимать одно из двух логических значений — истинное (часто обозначается как 1) или ложное (часто обозначается как 0). Слова AND, OR, NOT определяют операции над логическими значениями (логические операции). Например, составное высказывание с И истинно только в том случае, если истинны два элементарных высказывания. Если хотя бы одно из этих утверждений ложно, то составное утверждение ложно. Не имеет значения, какими были первоначальные заявления. Истинность составного высказывания зависит только от адекватности (иногда истинностной ценности) исходных высказываний.
Поскольку существует только два логических значения, эти операции могут быть описаны таблицами.
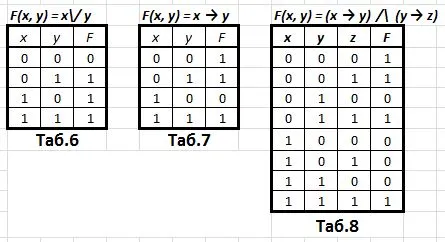
Операции AND, OR, NOT имеют «научные» названия (даже несколько для каждой операции 🙂 и специальные названия (в примерах A, B обозначают определенные логические значения):
НЕ: отрицание, инверсия. Нотация: ¬ (например, ¬A),
AND: конъюнкция, логическое умножение.
Обозначается /\ (например, A /\ B) или & (например, A & B),
ИЛИ: деление, логическое сложение.
Обозначается \/ (например, A \/ B).
В математике используются и другие логические операции.
Каждая логическая операция может быть определена своей собственной таблицей. Вот еще два примера логических операций:
1) Умозаключение (entailment) — обозначается → (например, A → B). Выражение A → B истинно, если A ложно ИЛИ B истинно. То есть, A → B означает то же самое, что (¬A)\/B. См. таблицу. 4.
3. Свойства логических выражений и таблиц истинности.
Приведенный ниже список НЕ претендует на исчерпывающую полноту, но, надеюсь, он достаточно репрезентативен.
3.1 Общие свойства
1) Существует ровно 2 n различных наборов значений для n логических переменных.
2) Таблица истинности для логического выражения с n переменными содержит n+1 столбцов (по одному столбцу для каждой переменной + 1 столбец для значения выражения) и 2 n строк (по одной строке для каждого набора значений переменных).
1) Если хотя бы одно из выражений, для которых выполняется дизъюнкция, истинно для набора значений переменных, то вся дизъюнкция истинна для этого набора значений.
2) Если все выражения в списке ложны для данного набора значений переменных, то дизъюнкция этих выражений также ложна.
3) Значение дизъюнкции не зависит от набора выражений, к которым она применяется.
4) При вычислении дизъюнкции выражений эти выражения могут быть сгруппированы произвольно — значение дизъюнкции не меняется.
5) Предположим, что все выражения, к которым применяется дизъюнкция, являются различными переменными или их отрицаниями. Тогда существует ровно один набор значений переменных, для которых дизъюнкция ложна. Переменная в этом наборе имеет значение 1, если она входит в дизъюнкцию с отрицанием, и значение 0 в противном случае.
1) Если хотя бы одно из выражений, к которым применяется конъюнкция, ложно для набора значений переменных, то вся конъюнкция ложна для этого набора значений.
2) Если все выражения в списке истинны для заданного набора значений переменных, то конъюнкция этих выражений также истинна.
3) Значение конъюнкции не зависит от набора выражений, к которым она применяется.
4) Когда вычисляется конъюнкция выражений, эти выражения могут быть сгруппированы как угодно — значение конъюнкции не меняется.
5) Пусть все выражения, к которым применяются ссылки, являются различными переменными или их отрицаниями. Тогда существует ровно один набор значений переменных, для которых связь истинна. Переменная в этом наборе имеет значение 1, если она входит в связь без отрицания, и значение 0 в противном случае.
1) Импликация A →B эквивалентна дизъюнкции (¬A)\/B. Этот дизъюнкт также можно записать как ¬A \/B.
2) Импликация A →B равна 0 (ложна), только если A = 1 и B = 0. Если A=0, то импликация A→B истинна при любом значении B. Если B=1, то заключение A→B верно для любого значения A.
1) Эквивалентность A ≡ B эквивалентна соединению двух следствий: A→B и B→A. Эту связку можно записать следующим образом: (A→B)/\(B→A).
2) Эквивалентность A ≡ B принимает значение 1 (истинно) только в том случае, если значения переменных A и B равны, т.е. A = B = 1 или A = B = 0.
Поэтому эквивалентность A ≡ B эквивалентна выражению (A/\B) \/ ((¬A) /\ (¬B) ).
3) Эквивалентность A ≡ B принимает значение 0 (ложно) только в том случае, если значения переменных A и B различны, т.е. A = 0 и B = 1 или A = 1 и B = 0. Поэтому эквивалентность A ≡ B эквивалентна выражению ¬ ( (A/\¬B) \/ (A /\¬B) ).
3.6 Построение выражения с заданной таблицей истинности
Для любого набора значений переменных можно построить выражение, которое будет истинным для всех наборов в этом наборе и только для этих наборов. Удобно записать это выражение в виде дизъюнкции связей, где в каждой связи (a) каждый член является одной переменной или ее отрицанием и (b) содержит все переменные.
Конъюнкция
Рассмотрим два утверждения: A = «Основателем алгебры логики является Джордж Буль»; B = «Исследования Клода Шеннона сделали возможным применение алгебры логики в информатике». Новое утверждение «Основателем алгебры логики является Джордж Буль, а исследования Клода Шеннона позволили применить алгебру логики в информатике», конечно, истинно только в том случае, если оба исходных утверждения истинны одновременно.
Самостоятельно определите, являются ли три приведенных выше утверждения истинными или ложными.
Сопряжение — это логическая операция, при которой каждые два высказывания дополняются новым высказыванием, которое истинно только в том случае, если истинны оба исходных высказывания.
Для обозначения союзов используются следующие символы. Например: A И B, A ? B, A — B, A&B.
Конъюнкция может быть описана в виде таблицы, называемой таблицей истинности:
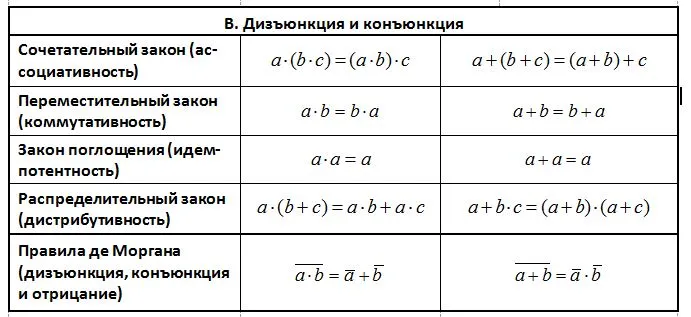
В таблице истинности перечислены все возможные значения исходных утверждений (столбцы A и B) с соответствующими двоичными числами, обычно расположенными в порядке возрастания: 00, 01, 10, 11. Последний столбец содержит результат логической операции для соответствующих операторов.
Это соединение также называется логическим умножением.
Дизъюнкция. Инверсия
Рассмотрим два утверждения: A = «Идея использования математических символов в логике принадлежит Готфриду Вильгельму Лейбницу», B = «Лейбниц является основателем двоичной арифметики». Очевидно, что новое утверждение «Идея использования математических символов в логике принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основателем двоичной арифметики» ложно только в том случае, если оба исходных утверждения ложны одновременно.
Самостоятельно определите, являются ли три приведенных выше утверждения истинными или ложными.
Дизъюнкция — это логическая операция, которая соединяет новое высказывание с каждым из двух высказываний, которое ложно только в том случае, если оба исходных высказывания ложны.
Символами дизъюнкции являются OR, ?, |, +. Например.
Дисъюнкция определяется следующей таблицей истинности:
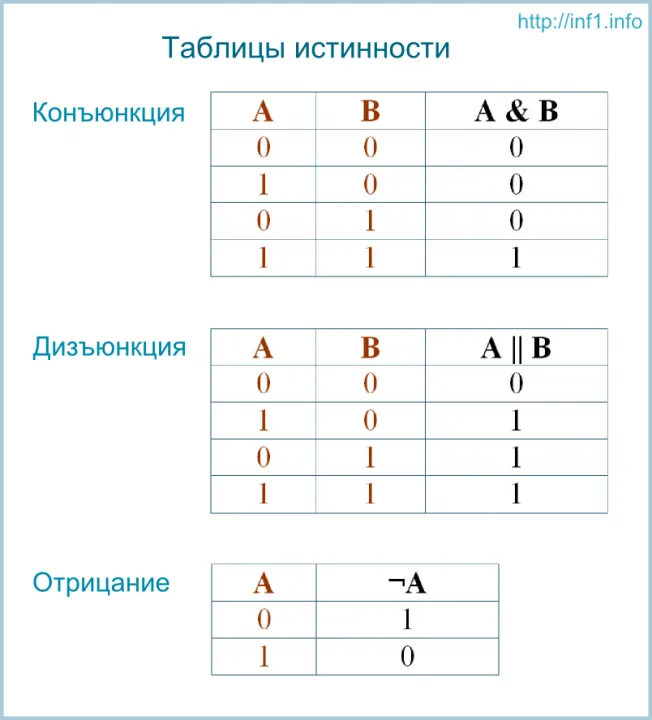
Дисъюнкцию также называют логическим дополнением. Подумайте, почему.
Инверсия
Инверсия — это логическая операция, которая сопоставляет каждое утверждение с новым утверждением, значение которого противоположно исходному утверждению.
Для инверсии используются следующие символы: NOT, ¬, -. Например: НЕ А, ¬ А,
Инверсия определяется следующей таблицей истинности:
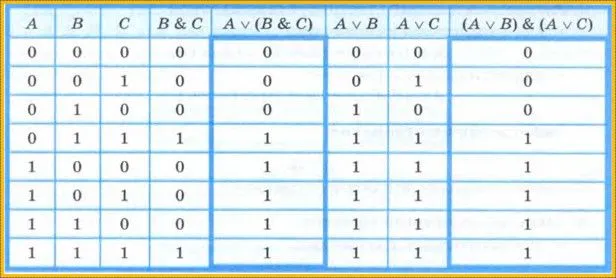
Инверсия также называется логическим отрицанием.
Отрицанием утверждения «У меня дома есть компьютер» является утверждение «Неверно, что у меня дома есть компьютер» или, что то же самое по-русски, «У меня дома нет компьютера».. Отрицанием утверждения «Я не знаю китайского языка» является утверждение «Ложно, что я не знаю китайского языка» или, что то же самое в русском языке, «Я знаю китайский язык». Отрицанием утверждения «Все восьмиклассники — отличники» будет утверждение «Неверно, что все восьмиклассники — отличники». Другими словами, «Не все восьмиклассники — отличники».
Поэтому отрицание может быть встроено в простое высказывание либо с помощью наречия «Это неправда, что…», либо с помощью обвинения, в этом случае к наречию добавляется глагол «не».
Мы можем записать любое составное высказывание в виде логического выражения — выражения, содержащего логические переменные, символы для логических операций и круглые скобки. Булевы операции в логическом выражении выполняются в следующем порядке: Инверсия, конъюнкция, дизъюнкция. Вы можете изменить порядок операций, установив круглые скобки.
Булевы операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
Использование частиц
Инверсия — это еще одна операция, ежедневно используемая пользователями компьютеров для обработки и передачи данных. Принцип преобразования отрицания: в каждую позицию помещается новое утверждение, противоположное исходному. Обращение вспять или отрицание означает, что за исходным утверждением следует инфинитив «нет» или слово «ложно» или «это». Объяснение логической операции:
- если первоначальное выражение является истиной, тогда его отрицание будет ложным;
- если исходное высказывание ложное, тогда его отрицание будет истинным.

Чтобы исправить символику инверсии, для логической операции используются специальные символы: «NOT», «A», «¬A». Логическое отрицание характеризуется определенными свойствами. Двойное отрицание» (обозначается «¬ ¬ A») является следствием суждения A. Оно обозначает тавтологию логической формы и равнозначно значению в булевой логике.
Предложение «У меня есть компьютер» имеет отрицание «Это неправда, что у меня есть компьютер» или «У меня нет компьютера». Предложение «Я не знаю японского» имеет отрицательное значение «Это неправда, что я не знаю японского» или «Я знаю японский». Другой пример обратного хода: «Все ученики 8-го класса — отличники». Отрицание можно построить следующим образом:
- «неверно, что все ученицы 8 класса — отличницы»;
- «не все ученицы 8 класса — отличницы».
При построении отрицания к простому высказыванию, будь то строфа из русского языка «неправда, что…» или отрицание к предикату, рекомендуется добавлять к глаголу частицу «не». Логическое умножение с помощью «и» должно выполняться перед сложением с помощью «или».
Составная операция может быть записана в виде выражения с переменными, символами и скобками. Необходимо соблюдать определенную последовательность действий:
- инверсия;
- конъюнкция;
- дизъюнкция.

Размещение круглых скобок изменяет порядок выполнения операции. По окончании выполненных операций делается вывод. Это составное выражение считается истинным во всех случаях, за исключением того, что ложь следует из истины. Функция позволяет объединить 2 простых утверждения, первое из которых считается условием, а второе — следствием.
Для вычисления результата составного высказывания достаточно определить только значение 1 составного элемента. Если в схеме с «и» используется неправильное простое высказывание, результат составного высказывания будет неправильным. Если значение простого символа в составном выражении с «или» истинно, то результат всего выражения истинен.
Закон Пирса
Булева функция, названная в честь Пирса, используется в информатике. Впервые он был введен в алгебру учеными в 1880 году. Он обозначается символом ↓, «или-нет». Свойства функции:
- формирование базиса для булевых функций 2-х неизвестных;
- построение других операций (отрицание: X↓X=¬X).

В информатике выражение представляется в виде элемента, называемого операцией 2IL-NE. Еще одна функция, которая часто используется в электронике, — это так называемая планка Шеффера. Операция состоит из 2 неизвестных или бинарного элемента. Эта надпись используется с 1913 года. Он обозначается символом |, что соответствует «и-нет».
Его важнейшие свойства:
- основа функции, состоящей из 2-х переменных;
- возможность построения иных высказываний (X ∣ X=¬X — отрицание).
В информатике эта операция используется для реализации схем, в которых используется общий, но дорогой элемент. Из всех существующих логических операций инверсия имеет приоритет. Операторы используют различные символы для выражения логических единиц. Эксперты решают проблемы своим умом и передают через услуги только конечный результат. Они используют схемы всех инструкций для обработки данных. Вычисления выполняются быстрее на компьютерах с мощным жестким диском.