Итак, мы разделили число на тысячи и вывели, сколько тысяч оно содержит. Теперь проделаем то же самое для сотен, десятков и единиц, изменив лишь несколько значений и вывод.
Что такое div и mod в паскале
Это вопрос: Что такое операции mod и div в Паскале? Как вы можете работать с нами?
Уровень сложности : легко.
Я постараюсь быть кратким и сразу скажу, что эти операции работают только с целыми числами, то есть с целыми числами и т.д. Во-первых, операция div: эта операция используется для нахождения целочисленной части деления. Как его следует понимать? Предположим, у нас есть код:
Зададим n равным 1. Почему? Как я уже сказал, div ищет целую часть деления, например, у нас 12 делится на 10, это дает 1.2. Целая часть деления равна 1. И вот что делает операция div, если мы скажем 12 div 2, ответ будет 6.0, целая часть равна 6. Это как деление 12 на 10, но в ответ записывается только целая часть деления.
Затем операция mod: эта операция уже ищет остаток от деления. Не думайте, что это дробь, не путайте!
Предположим, что существует код:
Рассмотрим небольшой пример: Предположим, существует число 123:
Обычно вы начинаете с последней цифры, в данном случае это 3. Чтобы вывести ее, мы должны сделать следующее:
То есть, мы делим 123 на 10, результат — 12,3, а остаток — 3. Первая цифра есть. Следующая цифра — 2. Сначала мы вычтем последнюю цифру, которая равна 3, с помощью div, а затем с помощью mod найдем вторую цифру:
То есть, сначала мы имеем 12 из-за div, а затем, используя mod, мы имеем 2. Последняя цифра может быть найдена следующим образом:
Например, вот так. Возможно, вы не сразу поймете это, но для этого нужно немного практики. Удачи! Спасибо за внимание!
Привет всем, как дела? Что случилось? Хорошо, я понял. Давайте не будем много говорить и будем дружелюбны, проходите, располагайтесь, чувствуйте себя комфортно. Снаружи солнце порабощает планету каждый день, я люблю это и с нетерпением жду еще одной теплой, грязной весны с большим количеством воды. Но есть золотая середина: тепло, птицы, растительность, легкая куртка. А как вы относитесь к весне? В этой части мы поговорим еще о двух функциях DIV и MOD, в предыдущей части мы говорили о математических операциях, сегодняшние функции также по сути являются таковыми. Вот так =)
DIV, MOD или обычное деление
DIV и MOD похожи на простое деление, но они все же для чего-то существуют, поэтому должна быть разница. Вспомните начальную школу и математику, когда вы учили только умножение и деление, когда вы еще не знали, что станете программистом и будете работать по принципу «ты — программист» или передатчиком. Шутки в сторону, давайте подумаем о делении столбцов. Возьмите 23 и разделите в столбик, как мы делали это в школе, на число 10.
Поэтому мы разделили 23 на 10. У нас осталось целое число 2 и остаток 3. Проще говоря, наш ответ — два целых числа и три десятых (2,3). Хорошо, это было обычное деление, но как бы это выглядело в случае MOD и DIV?
MOD — если разделить число с помощью функции MOD, то в качестве ответа мы получим остаток. В приведенном выше примере, если мы разделим число на Mod, а не на обычное деление, ответ будет 3.
DIV — наоборот, если мы делим с помощью DIV, то ответом будет только целая часть — 2.
Pascal
Откройте PascalABC и напишите программу
Объявите две переменные с целым типом данных
Затем присвойте значение переменной «a» и установите переменную «b» равной переменной «a».
Отлично, теперь выведите ответ для обычного деления на 100
Теперь выполним то же деление, но с DIV и MOD вместо обычного деления. Разделите переменную «a» на DIV, а переменную «b» на MOD и посмотрите, что получится.
Как видите, div обозначает целую часть, а mod — остаток.
Деление нацело ( div )
Целочисленное деление — это деление, при котором целое число делится на другое целое число. Результатом является целая часть его коэффициента.
Результатом операции является целое число, полученное в результате деления, или, точнее, целая часть результата деления.
15div3=5//результат обычного деления 514div3=4//результат обычного деления 4.6666663div2=1//результат обычного деления 1.5
Остаток от деления ( mod )
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю. 16: 7 = 2 (остаток 2) 23: 8 = 2 (остаток 7)
Результатом является целое число, которое представляет собой разность между делимым числом и следующим меньшим или равным ему целым числом, деленным на делитель.
15мод3=0//результат 15-1514мод3=2//результат 14-123мод2=1//score 3-2
Примечание: Операции div и mod применяются только к целым числам.
Используйте mod для определения кратности, т.е. делится ли число на четное число. Например, что числа 2, 6, 12, 24 делятся на два (четные числа). Оказывается, что все числа, которые не делятся на два, являются нечетными. Или числа 5, 10, 15, 20 кратны 5.
Рассмотрите несколько примеров использования этих операций в программировании.
Задание 1: Укажите размер файла в байтах и найдите количество полных килобайт, которые он занимает (1 килобайт = 1024 байта), используя операцию деления на целое число.
Решение:
Программаzadanie1;varb:Целое число;начатьчитать(b);b:=bdiv1024;пишите.(b);Конец.
Задача 2. Дано трехзначное число k. Найдите сумму цифр числа S.
Решение:
ПрограммаЗадание2;vark,s,c1,c2,c3:Целое число;начатьчитать(k);с1:=kмод10;с2:=(kdiv10)мод10;с3:=kмод100;s:=c1+c2+c3;пишите.(s);Конец.
Стандартные функции PascalABC
При написании программ на языке Pascal для выполнения вычислений можно использовать функции, доступные в среде программирования. Ниже приведен список наиболее полезных функций: Мощность, модуль, корень и другие.
| Имя функции | Тип результата | Описание функции |
| Abs(x) | совпадает с типом параметра | Модуль в Паскале определяется функцией Abs(x), которая возвращает абсолютное значение (модуль) x. Пример: Если x=6, то Abs(x)=6. |
| Sqr(x) | совпадает с типом параметра | Вторую силу в Паскале можно вычислить с помощью функции Sqr(x), которая возвращает квадрат x. Пример: Если x=5, то Sqr(5)=25. |
| Sqrt(x) | Квадратный корень в Паскале можно вычислить с помощью функции Sqrt(x), которая возвращает квадратный корень из x. Например, если x=49, то Sqrt(49)=7. Аргумент функции должен быть положительным числом. | |
| Мощность(x,y) | настоящий | Любая мощность в Pascal вычисляется с помощью Power(x,y). Оно возвращает x в степень y. Например, если основание x=2, а степень y=5, то Power(2,5)=32. В PascalABC мощность можно вычислить с помощью следующей нотации: 2**5 (две звездочки означают умножение). |
| Int(x) | настоящий | Возвращает целочисленную часть x |
| Random(x) | Целое число | Возвращает случайное целое число в диапазоне от 0 до x-1 |
| Случайный | настоящий | Возвращает случайное вещественное значение в диапазоне 0…1) |
| Frac(x) | настоящий | Возвращает дробную часть x |
| Truncate(x) | x-величина, целое число | Возвращает целочисленную часть x |
Задача 3. Вычислите значение y=5x 7-4x 2 +3
Функции в Паскале — мега переменные.
Функции отличаются от процедур тем, что после выполнения функции на ее место в коде ставится число, буква, строка и т.д. Набор встроенных функций Паскаля довольно обширен. Например, чтобы вычислить квадрат числа, можно использовать стандартную функцию sqr(x). Как вы, вероятно, уже поняли, sqr(x) принимает только один вещественный параметр — число.
Внимание. Функции должны быть назначены! Простая запись их как процедур в тексте программы ни к чему не приведет!
Структура функции показана на следующем рисунке.
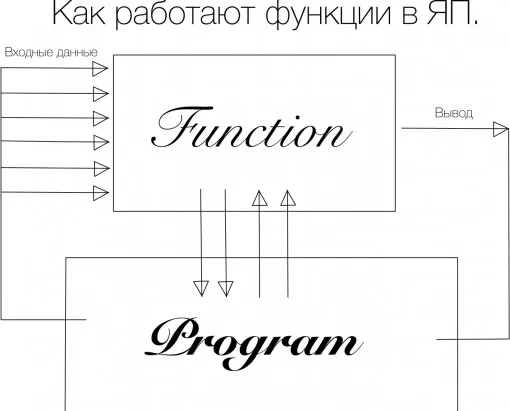
Если в программу необходимо включить новую уникальную функцию, она должна быть описана так же, как и процедура. О том, как создавать собственные процедуры и функции, вы можете узнать из 10 уроков. Ниже приведена таблица с основными стандартными функциями и процедурами Паскаля.
Операции div и mod.
Иногда нам нужно найти коэффициент или остаток от деления. В таких случаях необходимо использовать такие операции, как div и mod. Обратите внимание, что эти операции выполняются только с целыми числами.
Чтобы найти коэффициент деления, используется оператор div.
- 25 div 20 = 1;
- 20 div 25 = 0;
- 39 div 5 = 7;
- 158 div 3 = 52.
Mod
Чтобы найти остаток от деления, мы используем оператор mod.
- 25 mod 20 = 5;
- 20 mod 25 = 0;
- 39 mod 5 = 4;
- 158 mod 3 = 2.
Чтобы окончательно понять, с чем мы имеем дело, решите следующую задачу:
Задача 1: Найдите сумму цифр двузначного числа.
Поскольку эта задача очень проста, мы решим ее с помощью блок-схемы и программы.

program Sumoftwo; var Number, Num1, Num2, Sum: integer; begin write('Введите двузначное число: '); read(Number),<Возьмем число 25>Num1 := число div 10,<25 div 10 = 2>Num2 := число mod 10,<25 mod 10 = 5>Sum := Num1 + Num2,<2 + 5 = 7>write('Сумма двух чисел - ', Sum); end.
Задание 2: Найдите сумму цифр трехзначного числа.
Несколько более сложная версия предыдущей задачи. Наибольшую трудность представляет вторая цифра.
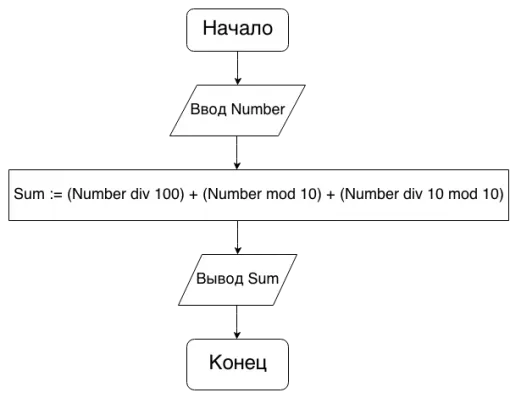
program Sumoftree; var Number, Sum: integer; begin write('Запишите трехзначное число: '); read(Number),<Возьмем число 255>Сумма := число div 100 + число mod 10 + число div 10 mod 10,<255 div 100 + 255 mod 10 12>write('Сумма трех чисел - ', Sum); end.
И это все. В следующем уроке мы рассмотрим функции PascalABC.Net.
Стандартные арифметические процедуры и функции Pascal
Здесь мы сосредоточимся на некоторых арифметических операциях.
-
Операция inc в Паскале, произносимая как инкремент, — это стандартная процедура в Паскале, обозначающая увеличение на единицу.
Пример операции inc:
x:=1;инк.(x);пишите.(х)
Более сложное использование процедуры inc: inc(x,n), где x — порядковый тип, а n — целочисленный тип; процедура inc увеличивает x на n.
Пример использования функции odd:
начатьWriteLn(Любопытный(5));WriteLn(Любопытный(4));Конец.
begin WriteLn(Odd(5)); WriteLn(Odd(4)); end.
Пример использования процедуры sqr в Паскале:
varx:Целое число;начатьx:=3;пишите.(sqr(x));Конец.
var x:integer; begin x:=3; writeln(sqr(x)); end .
Формула такая: exp(ln(a)*n), где а — число, n — степень (а>0).
Однако с компилятором Паскаля abc простое умножение намного проще:
WriteLn(мощность(2,3));
Пример использования процедуры sqrt в Паскале:
varx:Целое число;начатьx:=9;пишите.(sqrt(x));Конец.
var x:integer; begin x:=9; writeln(sqrt(x)); end.
Математические операции
В Паскале, как и в большинстве языков программирования, основные математические операции рассматриваются несколько идиосинкразически — например, математические выражения должны записываться в одну строку, а не на нескольких уровнях, как это принято в классической математической нотации. Это достигается за счет более широкого использования скобок, что иногда разочаровывает новичков. Также всегда следует писать символ умножения *. Кроме того, параметры функции всегда должны быть заключены в скобки. Например:
Если компилятор не поддерживает tan.
Базовая арифметика
| Имя функции | Оператор | Пример | Примечание |
| добавить | + | 2+2 (=4) | |
| удалить | — | 18.3-11 (=7.3) | |
| Умножить | * | 7*8 (=56) | |
| Раздел | / | 7/8 (=0.875) | Результат всегда реальный |
| Целочисленная часть деления | div | 7 div 2 (=3) | |
| остальная часть дивизии | мод | 7 mod 2 (=1) |
Все операции сравнения возвращают булево значение, то есть их можно использовать в операторах ветвления и цикла, например.
if 2 + 2 = 4 then writeln (‘Два и два вместе дают четыре!’)
| Имя функции | Оператор | Пример |
| Соответствует | = | 2+2=4 |
| Не равны (?) | <> | 2+2<>5 |
| Больше, чем | > | 72>71.99 |
| Больше или равно | >= | x*x>=0 |
| Менее | 0 | |
| Меньше или равно | 1 |
Функции для преобразования действительных и целых чисел
Паскаль — это язык программирования со статической сильной типизацией. Это означает, что компилятор не выполняет преобразования значений между типами, что может привести к потере информации. Например, если вы подставите вещественное число в конструкцию, которая возвращает целочисленное значение, компилятор сообщит об ошибке, даже если число является целым. Итак, как мы видели выше, 13 и 11 равны 9, но 13.0 и 11 приведут к сообщению компилятора об ошибке! Чтобы избежать этого, вы должны явно указать преобразование вещественного числа в целое число с помощью следующих функций:
| Имя функции | Описание | Пример |
|---|---|---|
| Круглый(X) | Возвращает целочисленное значение, наиболее близкое к X | Round(1.7)=2, Round(-3.1)=3 |
| Int(X), Trunc(X) | Возвращает целочисленную часть X | Int(1.8)=1, Trunc(-11.3)=-11 |
| Пол(X) | Возвращает наибольшее целочисленное значение, которое не превышает X | Floor(1.7)=1, Floor(-3.1)=-4 |
| Ceil(X) | Возвращает наименьшее целочисленное значение, которое не меньше X | Ceil(1.7)=2, Ceol(-3.1)=-3 |
Логические и побитовые операции
Логические операции используются для объединения нескольких логических условий в одно.
| Имя функции | Оператор | Пример | Описание |
|---|---|---|---|
| Булевы AND, and, логическое умножение | и | (2+3=5) and (0>-1) | Истинно, если оба оператора истинны |
| Логическое ИЛИ, или логическое сложение | or | (2+2=5) ή (1=1) | Истинно, если хотя бы один из операторов истинен |
| Логическое ИЛИ, исключающее ИЛИ | xor | (2+2=5) xor (1=1) | Истинно, если в точности один из операторов истинен. |
| Отрицательный, логический НЕ, нет | не | не (2+2=5) | Истинно, если один из операторов ложен. |
Булевы операторы, применяемые к целочисленным типам, могут использоваться как побитовые операторы. Чтобы получить результат побитовой операции, необходимо представить операнды в двоичном виде (как они представлены в компьютере), а затем применить соответствующую операцию к соответствующим битам, где 1 — истина, 0 — ложь.
| 13 в бинарной системе становится | 1 | 1 | 1 |
| 11 в двоичном формате становится | 1 | 1 | 1 |
| 9 в двоичном исчислении будет | 1 | 1 |
Существуют также две другие операции сдвига битов:
| Имя функции | Оператор | Пример | Описание |
|---|---|---|---|
| Правый сдвиг | Шр | 14 Шр 2 (=3) | Сдвигает двоичные разряды первого оператора вправо на разряды второго оператора; соответствует целочисленной части деления на 2 |
| Левый сдвиг | шл | 7 шл 3 (=56) | Сдвигает двоичные биты первого оператора влево на биты второго оператора; соответствует умножению на степень 2. |
Алгебраические функции
Серым цветом выделены операции, которые не поддерживаются Turbo Pascal.
| Имя функции | Описание | Заменить (для Turbo Pascal) |
|---|---|---|
| Pi | Возвращает числовое значение (+3.1415929265353589793238462643383279 … с точностью, заданной текущей формулой) | |
| Abs(X) | Абсолютное значение (модуль) X | |
| Sign(X) | Признак X: 1, если X отрицательный, 1, если X положительный 0, если X = 0 | |
| Exp(X) | Экспонента X (e X) | |
| Ln(X) | Натуральный логарифм X | |
| Log2(X) | Логарифм X по основанию 2 | Ln(X)/Ln(2) |
| Log10(X) | Логарифм X по основанию 10 | Ln(X)/Ln(10) |
| LogN(X,Y) | Логарифм Y к основанию X | Ln(Y)/Ln(X) |
| Мощность(X,Y) | Мощность X Y | Exp(Y*Ln(X)) |
| Sqrt(X) | Квадратный корень из X | |
| Sqr(X) | X-квадрат | |
| Max(X,Y) | Большая часть X и Y | |
| Min(X,Y) | Меньше, чем X и Y |
Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы «Инфоурок»).
В настоящее время 54 287 учебных заведений имеют право на накопительную скидку (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы «Инфоурок»).
В настоящее время 54 287 учебных заведений имеют право на накопительную скидку (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.


«Креативные инструменты в PowerPoint»

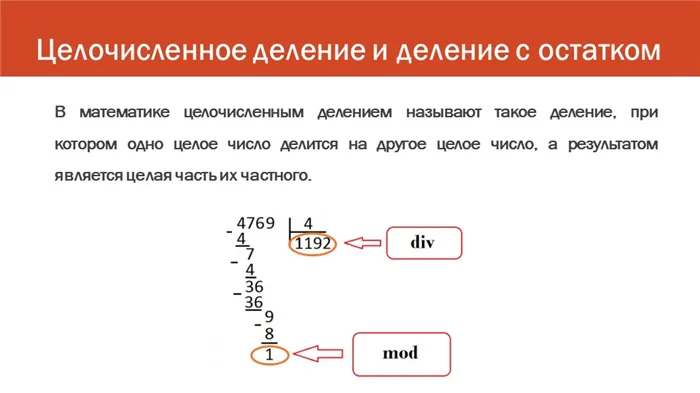
2 слайд Деление целых чисел и остатки В математике деление целых чисел — это деление одного целого числа на другое целое число, где результатом является целая часть результата.

3 Слайд DIV Основные правила — результат деления меньшего числа на большее равен нулю. MOD — результат деления меньшего числа на большее равен меньшему числу. Действие A mod 10 можно использовать для нахождения последней цифры любого целого числа.

4 Слайд Оператор DIV Оператор DIV используется для нахождения целочисленной части деления. Он работает только с целыми числами.
В данном примере n равно 1. Почему? Мы знаем, что DIV ищет целочисленную часть деления, которая в данном примере равна 12 делить на 10, что дает 1,2. Таким образом, целочисленная часть деления равна 1.

5 слайд Оператор MOD Оператор MOD используется для нахождения остатка от деления. Он работает только с целыми числами, не думайте, что это дробь, не запутайтесь!
В данном примере n равно 2. Почему? Мы знаем, что MOD ищет остаток от деления, т.е. в примере 12 делится на 10: значит, остаток от деления равен 2.

Слайд 6 Операторы DIV и MOD Если мы разделим 17 на 3, то получим 5.666666666…. Здесь записано целое число 5, которое является результатом операции DIV. Если мы разделим 17 на 3, то получим 5 как целое число и 2 как остаток. Результатом операции MOD является 2.

7 Слайд Примеры 35 div 10 = 36 div 5 = 77 div 3 = 345 div 10 = 123 div 12 = 44 div 1000 = 11 mod 2 = 32 mod 17 = 18 mod 3 = 1243 mod 100 = 45 mod 100 = 36 mod 10 = 3 7 25 34 10 0 1 1 15 0 43 45 6

8 Слайд Задание 1 Напишите программу, которая определяет количество цифр в последовательности натуральных чисел, делящихся на 6. Программа принимает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда есть число, кратное 6. https://inf-oge.sdamgia.ru/problem?id=120
Заключение
На сегодня это все, думаю, принцип ясен. Если что-то пойдет не так, не ругайте меня — просто напишите в комментариях. В следующей статье мы рассмотрим алгоритмы ветвления. Спасибо вам всем. До свидания =)

В этой статье мы рассмотрим операторы mod и div и их применение в решении задач. Мы рассмотрим несколько примеров с решениями, а также самостоятельно решаемые задачи.
Удачи в программировании.
- С помощью mod мы получаем остаток от деления числа a на число b.
Переменная s будет равна 5.
- С помощью оператора div мы получим целую часть от деления числа a на число b
Переменная s будет равна 2.
Использование mod при решении задач
- Чаще всего оператор mod используется для определения кратности числа и используется в условии (оператор IF)
Задача состоит в том, чтобы определить, является ли число, введенное с клавиатуры, четным.
Чтобы ответить на этот вопрос, разделите число a на mod, деленное на 2 (a mod 2), и сравните это значение с нулем. Условие таково: a mod 2 = 0.
Чтобы узнать, делится ли a на b без остатка, используйте условие:
- Также оператор mod используется для определения последней цифры числа
Задание: умножьте последнюю цифру числа на 10 и покажите результат.
Чтобы поместить последнюю цифру числа a в переменную, разделите число на mod на 10. Получим: b:=a mod 10 — последняя цифра числа оказывается в переменной b.
Если мы хотим отделить 2 последние цифры числа, мы делим его на 100; если мы хотим отделить 3 последние цифры, мы делим его на 1000 и так далее.
Чтобы узнать, заканчивается ли a на b, мы должны использовать условное выражение:
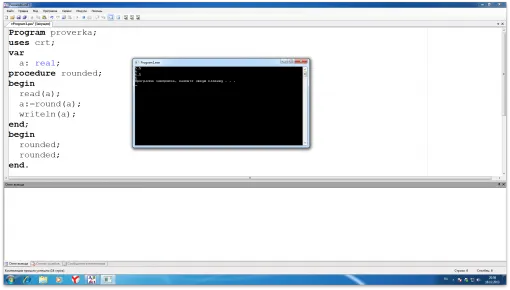
Проблема: Если число, введенное с клавиатуры, оканчивается на 5 и делится на 7, печатается «YES», в противном случае печатается «NO».
Используя рассмотренные условия и счетный цикл, мы можем решить следующую задачу:
Подсчитайте количество целых чисел, кратных 9 и оканчивающихся на 5 в диапазоне от 1 до 500.
Использование оператора div при решении задач
Задача: Вам дано трехзначное число. Выясните, является ли оно палиндромным («перевернутым»), т.е. числом, десятичная запись которого читается одинаково слева направо и справа налево.
Выделите первую цифру числа, разделив его на 100.
Отделите последнюю цифру, разделив ее на 10. Вторая цифра не нужна для решения задачи, потому что она не определяет, является ли число палиндромным или нет.
Задания, которые вы должны выполнять самостоятельно:
- Дано трехзначное число. Определить:
- является ли сума его цифр двузначным числом
- является ли произведение его цифр трехзначным числом
- больше ли числа a произведение его цифр
- кратна ли пяти сумма его цифр
- кратна ли сумма его цифр числу a
- Дано четырехзначное число. Определить:
- равна ли сумма двух первых его цифр сумме двух его последних цифр
- кратна ли трем сума его цифр
- кратно ли четырем произведение его цифр
- кратно ли произведение его цифр числу а