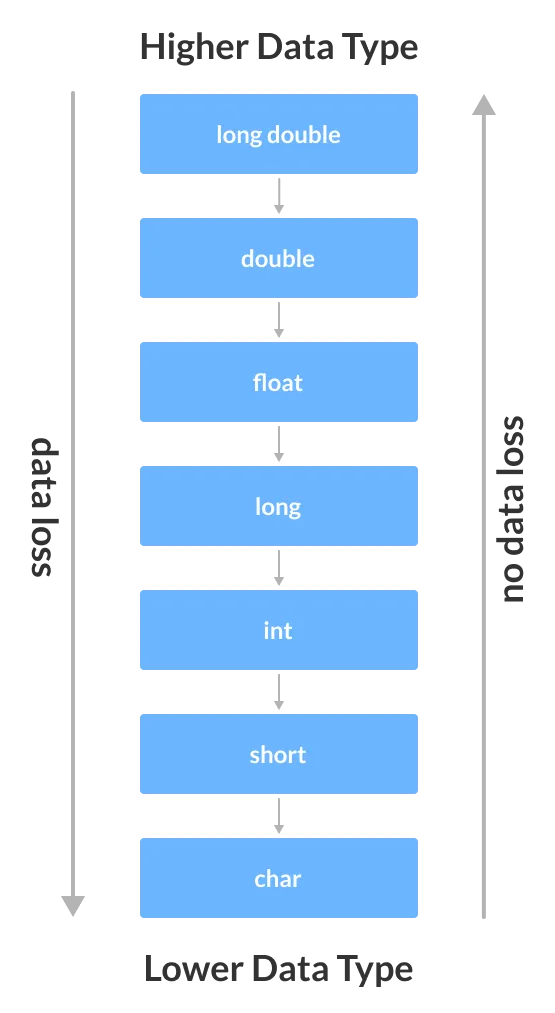
Положительные и отрицательные числа расположены симметрично относительно нуля. Поэтому максимальное и минимальное числа равны друг другу по модулю.
Представление чисел в компьютере
Рабочая память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из определенного количества однородных элементов. Эти элементы имеют два постоянных состояния, одно из которых соответствует значению ноль, а другое — значению один. Каждый из этих элементов служит для хранения одного из битов, одного бита двоичного числа. По этой причине каждый элемент ячейки называется битом или цифрой (рис. 1.2).
Рис. 1.2 Ячейка памяти
Существует несколько способов представления целых чисел в компьютере, которые отличаются количеством бит (для целых чисел обычно указывается 8, 16, 32 или 64 бита) и наличием или отсутствием знаковых цифр. Беззнаковое представление может использоваться только для неотрицательных целых чисел, в то время как отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, счетчики любого типа (например, количество символов в тексте), а также числа, представляющие дату и время, размер графических пикселей и т.д.
Максимальное значение неотрицательного целого числа достигается, когда все разряды клетки хранят единицы. Для n-значного представления это будет 2 n-1. Минимальное число соответствует n нулям, хранящимся в n битах памяти, и равно нулю.
Ниже приведены максимальные значения для n-разрядных беззнаковых целых чисел:

Чтобы представить беззнаковое целое число на компьютере, просто переведите его в двоичный формат и добавьте нули к стандартной цифре в левой части результата.
Пример 1. Номер 5310= 1101012в восьмизначной форме имеет вид:
То же число 53 с шестнадцатью цифрами будет записано следующим образом:
В знаковом представлении самый левый (старший) разряд присваивается знаку числа, а остальные разряды — самому числу. Если число положительное, в знаковом разряде ставится 0; если число отрицательное, в знаковом разряде ставится 1. Такое представление чисел называется прямым кодом.
В компьютерах прямые коды используются для хранения положительных чисел в запоминающих устройствах и для выполнения операций с положительными числами.
На сайте Федерального агентства по информационным и образовательным ресурсам (http://fcior.edu.ru/) размещен информационный раздел «Число и его арифметический код». Вы можете использовать этот ресурс для получения дополнительной информации по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, заменяющий операцию вычитания на сложение. С алгоритмом формирования дополнительных кодов можно ознакомиться на сайте Федерального информационно-образовательного ресурсного центра (http://fcior.edu.ru/) в разделе «Дополнительная информация о кодах».
Ссылки на ресурсы ЕС ЭОР
- интерактивный задачник, раздел «Системы счисления» (128659); http://school-collection.edu.ru/catalog/res/fc77f535-0c00-4871-b67c-fa2ecf567d46/?inter
- демонстрация к лекции «Представление целых чисел в памяти компьютера» (119430); http://school-collection.edu.ru/catalog/res/ecf4ab69-d8ac-40a8-b26a-2780aa70b33d/?inter
- тест по теме «Системы счисления» — «Система тестов и заданий N12» (134887); http://school-collection.edu.ru/catalog/res/6e89032a-2e09-4519-bb1e-653b4ecfd08f/?inter
- интерактивный задачник, раздел «Представление чисел» (119410); http://school-collection.edu.ru/catalog/res/c4939f11-5709-4fde-bc83-ceb614135d81/?inter
- тренировочный тест «Двоичная система счисления и представление чисел в памяти компьютера» (119342); http://school-collection.edu.ru/catalog/res/19d0fb95-871d-4063-961d-e7dc5725e555/?inter
- информационный модуль «Достоинcтва и недостатки двоичной системы счисления при использовании ее в компьютере» http://fcior.edu.ru/card/23457/dostoinctva-i-nedostatki-dvoichnoy-sistemy-schisleniya-pri-ispolzovanii-ee-v-kompyutere.html
Представление вещественных чисел
Любое действительное число A можно записать в экспоненциальной форме:
m — мантисса числа; q — основание системы счисления; p — порядок числа.
Например, число 472 ООООООО может быть представлено как: 4,72 — 10 8, 47,2 — 10 7, 472,0 — 10 6 и т.д.
Возможно, вы сталкивались с экспоненциальной нотацией при расчетах на калькуляторе, и ответ имеет вид 4,72Е+8.
Символ «E» здесь обозначает основание десятичной системы счисления и означает «умноженное на десять в степени десяти».
Приведенный выше пример показывает, что позиция стороны в числе может меняться.
В целях единообразия гадание обычно записывается в виде дроби с одной ненулевой цифрой после запятой. В этом случае число 472 ООО будет представлено как 0,472 — 10 9.
Вещественное число может занимать 32 или 64 разряда в памяти компьютера. В этом случае биты используются для хранения префикса предиктора, префикса порядка, префикса порядка и префикса предиктора.
Пример:

Диапазон представления вещественных чисел определяется количеством бит, выделенных для хранения порядка числа, а точность определяется количеством бит, выделенных для хранения предиктора.
Максимальное значение заказа для приведенного выше примера составляет 11111112= 12710и, следовательно, максимальное значение числа
0,11111111111111111111111 — 10 1111111
Попробуйте самостоятельно определить десятичный эквивалент этого значения.
Широкий спектр представлений вещественных чисел важен для решения научных и технических задач. Однако следует понимать, что алгоритмы обработки таких чисел более сложны по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Компьютер использует множество различных методов для представления целых чисел, которые отличаются количеством цифр (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Чтобы представить беззнаковое целое число, его необходимо преобразовать в двоичное, а полученное число обнулить слева до стандартной разрядности.
В знаковом представлении старший разряд резервируется для знака числа, а остальные разряды — для самого числа. Если число положительное, то вместо знака подставляется 0, если число отрицательное, то вместо знака подставляется 1. Положительные числа хранятся в компьютере в прямом коде, а отрицательные — во вспомогательном.
При хранении вещественных чисел в компьютере цифры используются для хранения знака последовательности чисел, самой последовательности чисел, знака гадающего и знака гадаемого. Таким образом, каждое число записывается следующим образом:
m — мантисса числа; q — основание системы счисления; p — порядок числа.
2.2. Представление вещественных чисел
Любое действительное число A можно записать в экспоненциальной форме:
m — предикат числа; q — основание системы счисления; p — порядок числа.
Например, число 472 000 000 можно представить следующим образом: 4,72 — 10 8, 47,2 — 10 7, 472,0 — 10 6 и т.д.
Возможно, вы сталкивались с экспоненциальной нотацией при расчетах на калькуляторе, и ответ имеет вид 4,72Е+8.
Символ «E» здесь обозначает основание десятичной системы счисления и означает «умноженное на десять в степени десяти».
Приведенный выше пример показывает, что позиция стороны в числе может меняться.
Для единообразия мантисса обычно записывается как обыкновенная дробь с ненулевой цифрой после десятичной точки. В данном случае число 472 000 000 представлено как 0,472 — 10 9.
Вещественное число может занимать 32 или 64 разряда в памяти компьютера. В этом случае биты используются для хранения префикса предиктора, префикса порядка, префикса порядка и префикса предиктора.
Пример:
Диапазон представления вещественных чисел определяется количеством бит, выделенных для хранения порядка числа, а точность определяется количеством бит, выделенных для хранения предиктора.
Максимальное значение заказа для приведенного выше примера составляет 11111112= 12710и, следовательно, максимальное значение числа
0,11111111111111111111111 — 10 1111111
Попробуйте самостоятельно определить десятичный эквивалент этого значения.
Широкий спектр представлений вещественных чисел важен для решения научных и технических задач. Однако следует отметить, что алгоритмы обработки таких чисел более энергоемки, чем алгоритмы обработки целых чисел.
САМОЕ ГЛАВНОЕ
Компьютер использует множество различных методов для представления целых чисел, которые отличаются количеством цифр (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Чтобы представить беззнаковое целое число, его необходимо преобразовать в двоичное, а полученное число обнулить слева до стандартной разрядности.
В знаковом представлении старший разряд резервируется для знака числа, а остальные разряды — для самого числа. Если число положительное, то вместо знака подставляется 0, если число отрицательное, то вместо знака подставляется 1. Положительные числа хранятся в компьютере в прямом коде, а отрицательные — во вспомогательном.
При хранении вещественных чисел в компьютере цифры используются для хранения знака последовательности чисел, самой последовательности чисел, знака гадающего и знака гадаемого. Таким образом, каждое число записывается следующим образом:
m — мантисса числа; q — основание системы счисления; p — порядок числа.
Вопросы и задания
1. обратитесь к материалу презентации параграфа в электронном приложении к учебнику. Используйте этот материал для подготовки ответов на вопросы и задания.
2. как целые положительные и отрицательные числа представлены в памяти компьютера?
3. любое целое число может быть представлено как действительное число, но с дробью ноль. Обоснуйте целесообразность тех или иных способов представления целых чисел в компьютере.
4. представить число 6310в беззнаковой 8-значной форме.
5. находить десятичные эквивалентные числа с их прямыми кодами, записанными в беззнаковом 8-значном формате:
(a) 01001100; (b) 00010101010101.
6. какое из чисел 4438, 1010102, 25610можно хранить в 8-значном формате?
7. запишите следующие числа в натуральной форме:
(a) 0,3800456 — 10 2, (b) 0,245 — 1 0-3, (c) 1,256900E+5, (d) 9,569120E-3.
8. напишите число 2010.010210пятью различными способами в экспоненциальной форме.
9 Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — нормальной дробью с ненулевым десятичным знаком:
10 Нарисуйте схему, связывающую ключевые понятия, рассмотренные в этом разделе.