Как вы можете рассчитать стандартное отклонение, если вам известна дисперсия? Как мы помним, возьмите квадратный корень из. То есть, стандартное отклонение равно:
Описательные статистики
Пусть X будет1, Х2. Xn— выборка независимых случайных величин.
Расположите эти переменные в порядке возрастания, т.е. создайте вариационный ряд:
Элементы вариационного ряда (*) называются порядковыми статистиками.
Значения d(i)= X(i+1)— X(i)называются расстояниями или интервалами между порядковыми статистиками.
Дисперсия выборки — это величина
Другими словами, диапазон — это расстояние между максимальным и минимальным значениями в наборе вариаций.
Среднее выборочное равно: = (X1+ Х2+. + Xn) / n
Среднее арифметическое
Большинство из вас, вероятно, использовали такую важную описательную статистику, как среднее значение.
Среднее значение является очень информативной мерой «центральности» наблюдаемой переменной, особенно когда сообщается ее доверительный интервал. Исследователю нужны статистические данные, позволяющие сделать выводы о населении. Одним из таких статистических показателей является среднее значение.
Доверительный интервал для среднего представляет собой диапазон значений вокруг оценки, в котором находится «истинное» (неизвестное) среднее значение популяции при заданном уровне доверия.
Например, если выборочное среднее равно 23, а нижняя и верхняя границы доверительного интервала при p=.95 равны 19 и 27 соответственно, можно сделать вывод, что интервал с границами 19 и 27 включает среднее значение популяции с вероятностью 95%.
Если вы устанавливаете более высокий уровень доверия, интервал становится шире, так что вероятность того, что он «накроет» неизвестное среднее значение популяции, увеличивается, и наоборот.
Например, известно, что чем более «неопределенным» является прогноз погоды (т.е. чем шире доверительный интервал), тем больше вероятность того, что он будет точным. Обратите внимание, что ширина доверительного интервала зависит от размера выборки и изменчивости данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение дисперсии наблюдаемых значений снижает надежность оценки.
Расчет доверительных интервалов основан на предположении, что наблюдаемые значения являются нормальными. Если это предположение не выполняется, оценка может быть плохой, особенно для небольших выборок.
Если размер выборки увеличивается, скажем, до 100 или более, качество оценки улучшается даже без предположения о нормальности выборки.
Если данные не обобщены, довольно трудно «почувствовать» числовые показатели. График часто полезен в качестве отправной точки. Мы также можем обобщать информацию, основываясь на важных характеристиках данных. В частности, если бы мы знали, из чего состоят вычисляемые значения или какова дисперсия наблюдений, мы могли бы получить представление о данных.
Среднее арифметическое, которое очень часто называют просто «средним», получается путем сложения всех значений и деления этой суммы на количество значений в наборе.
Это можно проиллюстрировать с помощью алгебраической формулы. Набор из n наблюдений переменной X может быть представлен следующим образом: X1, X2, X3,. Xn. Например, X может использоваться для обозначения роста человека (см), X1обозначает рост 1-го индивидуума, а Xi— рост i-го человека. Формула для определения среднего арифметического результатов наблюдений (произносится как «Х с дефисом»):
Это выражение можно сократить:
При i = 1 — i = n. Это выражение часто еще больше уменьшается:
Медиана
Если данные упорядочены по размеру, начиная с наименьшего и заканчивая наибольшим значением, медиана также является характеристикой среднего в упорядоченном наборе данных.
Медиана делит ряд упорядоченных значений в середине на равное количество значений выше и ниже (слева и справа от медианы на числовой оси).
Расчет медианы прост, если количество наблюдений nнечётный. Это равно количеству наблюдений (n + 1)/2 в нашем упорядоченном наборе данных.
Например, если n = 11, то медиана равна (11 + 1)/2, что является 6-м наблюдением в упорядоченном наборе данных.
Если nравномерното, строго говоря, медианы не существует. Однако обычно он рассчитывается как среднее арифметическое двух соседних средних наблюдений в упорядоченном наборе данных (т.е. наблюдений с номерами (n/2) и (n/2 + 1)).
Например, если n = 20, то медиана — это среднее арифметическое наблюдений с номерами 20/2 = 10 и (20/2 + 1) = 11 в упорядоченном наборе данных.
Стандартное отклонение (Standard Deviation)

Стандартное отклонение (σ, s) — это мера вариации в наборе числовых данных. Проще говоря, насколько далеко точки данных находятся от среднего арифметического (Mean). Его также можно назвать мерой центральной тенденции: Чем меньше стандартное отклонение, тем больше данные «группируются» вокруг центра (среднего значения). Чем больше отклонение, тем больше разброс значений.
Стандартное отклонение в статистике
Коэффициент рассчитывается по следующей формуле:
$σ = \sqrt^n(x_i — \bar)^2>>где$ $$пространство (малый масштаб)\пространство-{типичная расовая дивергенция$ $$пространство-{концентрированная дивергенция$ $$x\пространство-{пространство-{расовый элемент рамки выборки$ $$x\bar-{пространство-{среднее значение} рамки выборки$ $$n\пространство-{пространство-{число} элементов рамки выборки$$.
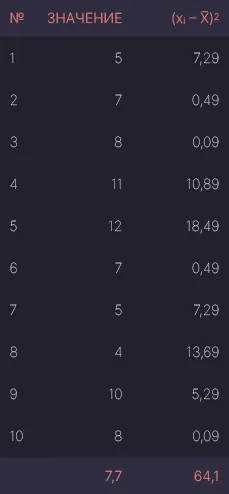
Пример. У нас есть выборка из 10 наблюдений, показывающая, сколько килограммов помидоров собрали садоводы в этом месяце:
Среднее значение выборки составит 7,7:
$\bar = (5 + 7 + 8 + 11 + 12 + 7 + 5 + 4 + 10 + 8) / 10 = $7,7
Используя эту формулу, мы вычисляем квадрат разницы между i-й записью в выборке и средней ценой. Для первого появления это будет выглядеть, например, так:
$x_i — \bar = (5 — 7.7)^2 = 7.29$
Причина, по которой мы возводим разницу в квадрат, заключается в том, что большие отклонения от среднего значения в некотором смысле более «наказуемы». Возведение в квадрат также приводит к одинаковому расчету для отклонений в обоих направлениях (положительных и отрицательных), т.е. расстояние от среднего для отрицательного и положительного числа рассчитывается правильно в обоих случаях.
Сумма значений в правом столбце равна 64,1, поэтому, согласно формуле, стандартное отклонение одинаково:
Стандартное отклонение в Машинном обучении
Представьте себе, если бы «помидорная» перепись была проведена в более широком масштабе и исследователи собрали данные по всей климатической зоне. Несколько человек, выбравших по 2 кг, и те, кто выбрал 50. В среднем садоводы собирали по 25 кг.
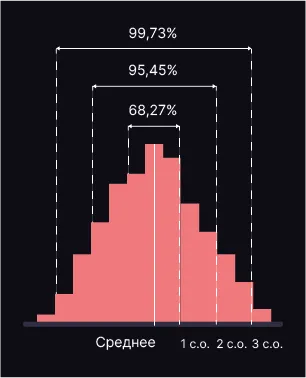
При построении модели прогнозирования урожая стандартное отклонение улучшает наши гипотезы в соответствии со следующими принципами:
- С вероятностью 68% следующее наблюдение будет лежать в пределах одного отклонения от среднего (25 ± 6,41), то есть в диапазоне 18,59 — 31,41 кг.
- С вероятностью 95% следующий дачник сообщит, что собрал томатов. в пределах двух стандартных отклонений от среднего значения (25 ± 2 × 6,41), то есть 12,18 – 37,82 кг.
- С вероятностью 99% размер урожая будет лежать в пределах 3 отклонений (25 ± 3 × 6,41): 5,77 – 44,23 кг.
Свойства дисперсии
Свойство 1. Дисперсия константы A равна 0 (нулю).
Свойство 2: Если случайную величину умножить на константу A, то дисперсия этой случайной величины увеличивается на коэффициент A 2. Другими словами, постоянный множитель можно вычесть из знака дисперсии путем возведения в квадрат.
Свойство 3. Если к случайной величине добавить (или вычесть) константу A, дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их разностей.
Свойство 5: Если случайные величины X и Y независимы, то дисперсия их разности также равна сумме их разностей.
Среднеквадратичное (стандартное) отклонение
Если взять квадратный корень из дисперсии, то получится стандартное отклонение (СКО). Его также называют стандартным отклонением и сигмой (с греческого). Общая формула для стандартного отклонения в математике выглядит следующим образом:
На практике формула для стандартного отклонения выглядит следующим образом:
Как и в случае с дисперсией, существует несколько иной метод расчета. Однако, когда выборка становится больше, разница исчезает.
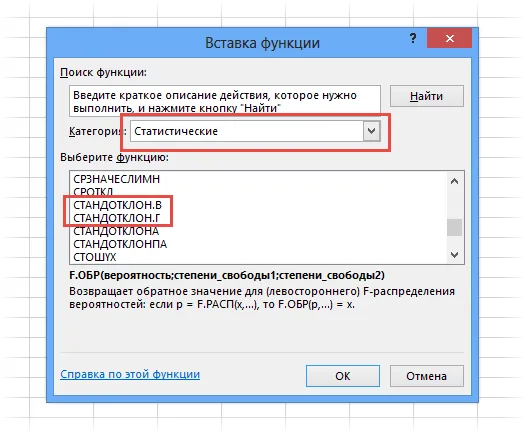
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Чтобы рассчитать стандартное отклонение, просто возьмите квадратный корень из дисперсии. Однако в Excel есть готовые функции: СТАНДОТКЛОН.D и СТАНДОТКЛОН.B (для генеральной совокупности и выборочной совокупности, соответственно).
Стандартное отклонение имеет те же единицы измерения, что и анализируемый показатель, и поэтому сопоставимо с исходными данными.
Среднее квадратическое отклонение
Среднеквадратическое отклонение равно квадратному корню из дисперсии: При определении среднего квадратического отклонения при достаточно большом объеме изучаемой совокупности (n>30) Применяются следующие формулы: — простое (или невзвешенное) стандартное отклонение; — взвешенное стандартное отклонение, где: xi— значения исследуемого признака (вариации); n — размер статистической совокупности; x — средняя арифметическая.
Стандартное отклонение описывает дисперсию значений по отношению к среднему значению (математическому ожиданию). Его называют σ(x) или s(x).
Свойства среднего квадратическоо отклонения
- σ(const)=0
- σ(x)≥0
- σ(k*x)=k*σ(x)
- Среднее квадратическое отклонение суммы или разности двух независимых случайных величин равна квадратному корню от суммы квадратов квадратических отклонений этих величин.
Стандартное отклонение может быть рассчитано с помощью различных калькуляторов в зависимости от исходных данных. Наиболее распространенными являются.
- Равномерное распределение Дисперсия: Среднеквадратическое отклонение:
- Нормальное распределение Дисперсия: DX = σ 2
Среднеквадратическое отклонение:
Среднеквадратическое отклонение:
Среднее квадратическое отклонение случайных величин
- Дискретной случайной величины Дисперсия d=∑x 2ipi— Mx 2 Среднее квадратическое отклонение σ(x) = sqrt(DX)
- Непрерывной случайной величины Дисперсия Среднее квадратическое отклонение σ(x) = sqrt(DX)
- Системы случайных величин Выборочные средние: x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3 y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3 Дисперсии: σ 2x= (20 2 (2 + 4) + 30 2 (6 + 3) + 40 2 (6 + 45 + 4) + 50 2 (2 + 8 + 6) + 60 2 (4 + 7 + 3))/100 — 42.3 2 = 99.71 σ 2y= (11 2 (2) + 16 2 (4 + 6) + 21 2 (3 + 6 + 2) + 26 2 (45 + 8 + 4) + 31 2 (4 + 6 + 7) + 36 2 (3))/100 — 25,3 2 = 24,01 Стандартные отклонения: σx= 9,99 и σy= 4.9
- Пример задания
- Видеоинструкция
- Пример оформления
- построить гистограмму частот;
- вычислить несмещенную оценку дисперсии и СКО;
- вычислить среднее абсолютное отклонение θ;
- вычислить коэффициент вариации V;
- определить размах варьирования R.