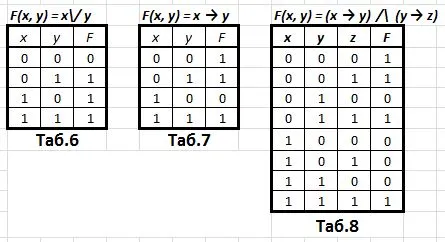
В булевой алгебре есть только два значения — true и false. В английском языке true обозначает истину, а false — ложь. Оба значения являются булевыми. Обычно значение true обозначается единицей, а false — нулем.
Алгебра логики
Логическая алгебра является частью науки дискретной математики, которая быстро развивается. Дискретная математика занимается изучением свойств конечных структур, которые встречаются как в математике, так и в ее приложениях.
- Заметим, что классическая математика, в основном, занимается изучением свойств объектов непрерывного характера, хотя само деление математики на классическую и дискретную в значительной мере условно, поскольку между ними происходит активная циркуляция идей и методов, часто возникает необходимость исследовать модели, обладающие как дискретными, так и непрерывными свойствами.
Структуры, изучаемые в дискретной математике, могут включать конечные множества, конечные графы, математические модели преобразователей информации, такие как конечные автоматы или машины Тьюринга, и так далее. Математический аппарат логической алгебры широко используется в информатике, особенно в таких областях, как проектирование компьютеров, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и др. Алгебра логики.
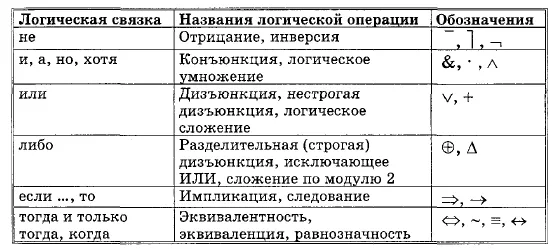
Понятие пропозиции Алгебра логики изучает свойства функций, аргументы и значения которых принадлежат заданному множеству из двух элементов (например,
Именно он построил одну из ветвей формальной логики в терминах некой «алгебры», аналогичной, но не сводимой к алгебре чисел. Алгебра в широком смысле — это наука об общих операциях, которые, по аналогии со сложением и умножением, можно выполнять не только с числами, но и с другими математическими объектами.
Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т.д. Дж. Буль (1815-1864) Долгое время алгебра логики была известна лишь узкому кругу специалистов.
Полный цикл лекций по высшей математике можно найти по этой ссылке:
Почти через 100 лет после создания алгебры логики Дж. Булем выдающийся американский математик и инженер Клод Шеннон (1916-2001) в 1938 году показал, что алгебра логики применима для описания самых разных процессов, включая работу релейных схем и схем электронных ламп. Исследования в области алгебры логики тесно связаны с изучением высказываний (хотя высказывания являются предметом формальной логики).
- С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примерами высказываний на естественном языке являются предложения «Сегодня светит солнце» или «Трава растет». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в нашем примере погоды и окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».
Однако установление истинности утверждения — задача далеко не простая. Например, утверждение «Число» определяется геометрией, и в геометрии Евклида это утверждение истинно, а в геометрии Лобачевского — ложно. Так что же такое высказывание в формальной логике?
Определение 1. Высказывание — это языковая единица, о которой полезно говорить о ее истинности или ложности (Аристотель).
Вы можете найти эти страницы полезными:
Это словесное определение, которое не является математически точным, кажется удовлетворительным только на первый взгляд. Она сводит проблему определения высказывания к проблеме определения того, является ли конкретная языковая единица истинной или ложной. Если мы принимаем каждое утвердительное высказывание за утверждение, это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение ложно» нельзя приписать истинное значение без возникновения противоречия. Ведь если предположить, что предложение истинно, то это противоречит его смыслу. Однако если предположить, что предложение ложно, то из этого следует, что оно на самом деле истинно.
Пример 1.
Следующие два следствия ложны, потому что их предпосылки истинны, а заключения ложны:
Может показаться странным, что высказывание «Если А, то В>>всегда истинно, если условие (высказывание L) ложно. Но для математика это вполне естественно. На самом деле, правильно размышляя, вы можете перейти от ложной предпосылки к истинному и ложному утверждению. Предположим, 1 = 2, тогда 2 = 1. Сложите эти уравнения и получите 3 = 3, т.е. ложная посылка превращается в истинное утверждение путем преобразования тождества.
Большинство математических теорем являются следствиями. Однако королларии, в которых посылка (условие) и заключение (следствие) являются пропозициями без взаимной (существенной) связи, не могут играть важную роль в науке. Это бесплодные предложения, потому что они не ведут к выводам с более глубоким содержанием.
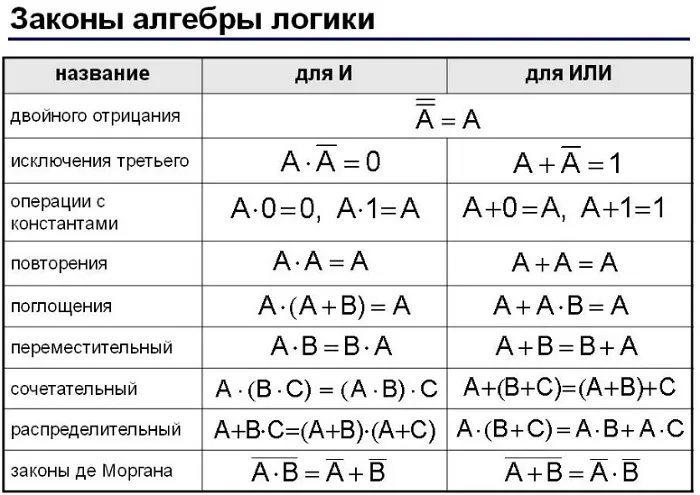
Логические формулы. Законы алгебры логики
Математики используют слово «алгебра» для обозначения науки, которая имеет дело с определенными типами объектов и операциями над ними. Школьная алгебра (алгебра действительных чисел), например, имеет дело с действительными числами и операциями над ними. Объектом нашего изучения являются высказывания, операции над ними и логические функции. В предыдущих разделах мы использовали буквы для обозначения утверждений. Как и в алгебре действительных чисел, мы вводим следующие определения.
Определение 9. Логическая переменная — это переменная, значением которой может быть любое выражение.
Логические переменные (далее «переменные») обозначаются латинскими буквами, иногда с подписями, как обычные алгебраические переменные:
Понятие логического типа является формализацией понятия составного высказывания. Давайте представим его индуктивно. Определение 10. Логический тип — это: 1) любая логическая переменная плюс одна из двух логических констант 0 (ложь) и 1 (истина); 2) если A и B — типы, то B и A*B — тоже типы, где символ «*» обозначает одну из бинарных логических операций. Например, формула — это следующее выражение:
Определение 11. Формулы A и B зависят от одного и того же набора переменных и имеют одинаковые значения.
Для обозначения эквивалентности формул используется символ эквивалентности, например, A B. Далее показано, что любая формула может быть преобразована в эквивалентную формулу с помощью только аксиоматически введенных операций.
1) Законы коммутативности
2) Законы ассоциативности
3) Законы поглощения (нулевой и единичный)
4) Законы дистрибутивности
5) Закон противоречия
6) Право исключенного третьего лица
7) Законы идемпотентности
8) закон двойного отрицания
9) Закон де Моргана
10) Законы поглощения.
Каждый из этих законов может быть легко доказан с помощью таблиц истинности.
Пример 2.
Мы хотим доказать первый закон де Моргана с помощью таблиц истинности. Давайте построим таблицу истинности для левой и правой частей закона.
Поскольку полученные столбцы совпадают, формулы в левой и правой частях закона одинаковы. Каждый из законов алгебры логики может быть доказан путем рассуждений.
Пример 3.
Доказательство первого закона абсорбции
Предположим, что правая часть истинна, т.е. истинна в соответствии с определением дизъюнкции.
Пусть левая часть верна. Тогда, согласно определению дизъюнкции, истинна либо формула, либо обе формулы одновременно.
Если оно ложно, то x может быть только истинным. Другим способом выведения законов являются преобразования тождеств. Пример 9. Первый закон поглощения можно вывести из законов поглощения единицы и распределения:
Методы решения логических задач Исходными данными для решения логических задач являются высказывания. Эти утверждения и отношения между ними могут быть настолько сложными, что их трудно понять без применения специальных методов.
Многие логические задачи предполагают рассмотрение множества конечных множеств и отношений между их элементами. Для решения таких задач часто используются таблицы или графики, и успешное решение во многом зависит от правильного выбора структуры таблицы или графика. Аппарат алгебры логики позволяет построить формальный, универсальный метод решения логических задач.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который можно обобщить как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
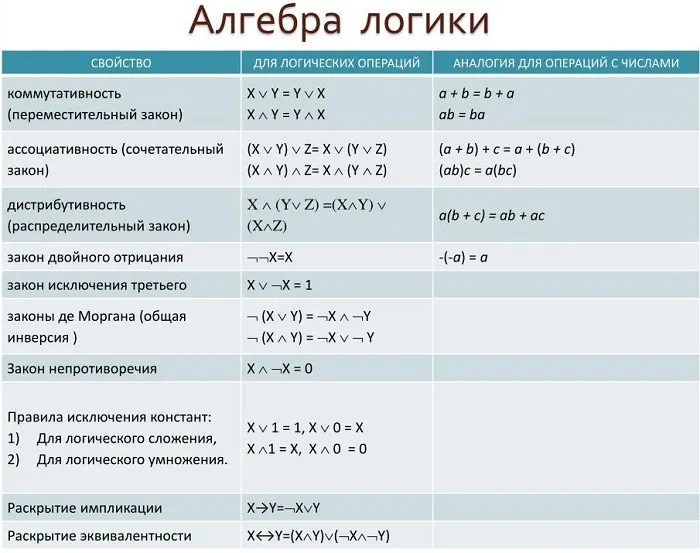
Законы алгебры логики
В этой области существует множество правил, но сегодня мы рассмотрим некоторые из наиболее важных.
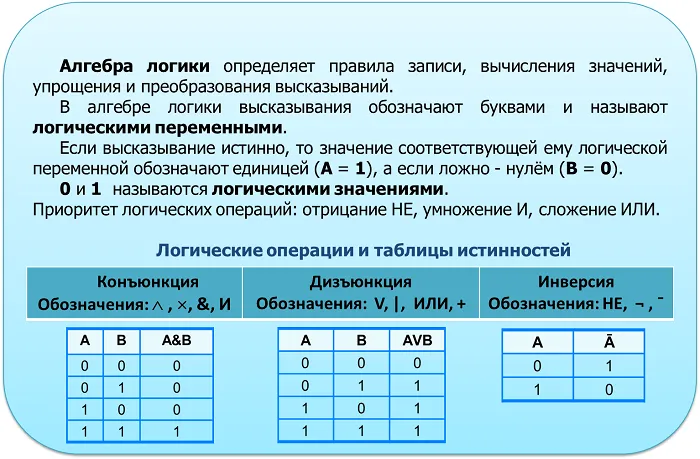
Закон сложения и вычитания предназначен для процесса сложения и вычитания. Суть этого правила заключается в том, что положения А и В могут быть изменены в операциях деления и соединения. Конкубинат — применяется, когда есть либо только акт развода, либо только акт соединения. Тогда вы можете обойтись без скобок или расставить скобки хаотично. Дистрибутивный закон — существует два типа этого правила: дистрибутив дизъюнкции над конъюнкцией и дистрибутив конъюнкции над дизъюнкцией. Первый тип похож на распределительный закон алгебры, но второй тип не похож, поэтому его необходимо доказать. Закон двойственности и инверсии (закон Моргана) — Основателем этого правила был шотландский математик и логик де Морган. Он разработал правило, которое соединяет логические операции конъюнкции (AND) и дизъюнкции (OR) с помощью отрицания. Основные законы алгебры логики перечислены в таблице:
Логические выражения
В информатике существует два типа утверждений: простые и сложные.

- Нью-Йорк — столица США (ложное);
- в России 1117 городов (верное).
Сложное утверждение относится к серии простых утверждений, связанных логическими процедурами.
Идет дождь, а у меня нет зонтика.