Найдите на доске следующие предметы: бабушку, Машу, дом и конверт. Каждый объект имеет свое свойство, значение и величину значения. Бабушка имеет свойство: старый, значение: возраст, значение: 55 лет. Маша тоже такая, она маленькая, рост 120 см. Существуют и другие объекты с аналогичными свойствами, ценностями и значениями.
Разнообразие отношений.
Человек может говорить не только о свойствах объекта, но и об отношениях этого объекта с другими объектами. Например:
- «Иван — сын Андрея»;
- «Эверест выше Эльбруса»;
- «Винни Пух дружит с Пятачком»;
- «21 кратно 3»;
- «Кострома такой же старинный город, как и Москва»;
- «текстовый процессор входит в состав программного обеспечения компьютера»;
- «один байт равен восьми битам».
В каждом из приведенных выше предложений дается название отношения, указывающее на характер связи между двумя объектами.
Отношения — это взаимная связь между двумя объектами.
Многие объекты могут быть связаны одним и тем же отношением. Соответствующее словесное описание может быть очень длинным, и тогда его трудно понять.
Предположим, что для мест A, B, C, D, E и F известно, что некоторые из них соединены железной дорогой: A соединен железной дорогой с C, D и E; E соединен железной дорогой с A, C, D и E.
Для наглядности существующие соединения («соединенные рельсами») могут быть представлены линиями на диаграмме отношений. Объекты в графе отношений могут быть представлены в виде кругов, овалов, точек, прямоугольников и т.д. (Рисунок 4).
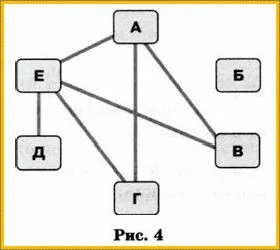
Некоторые названия отношений меняются, когда имена объектов меняются местами, например, «выше» — «ниже», «быть отцом» — «быть сыном». В этом случае направление связи указывается стрелкой на диаграмме связей.
Поэтому на рис. 4 каждая стрелка указывает от отца к сыну и, следовательно, отражает отношения «наличие отца», а не «наличие сына». Например, «Андрей — отец Ивана».
Стрелки можно не ставить, если можно сформулировать и соблюдать правило взаимного расположения объектов на диаграмме. Например, если на рис. 5 имена детей всегда находятся под именами их отцов, можно обойтись без стрелок.
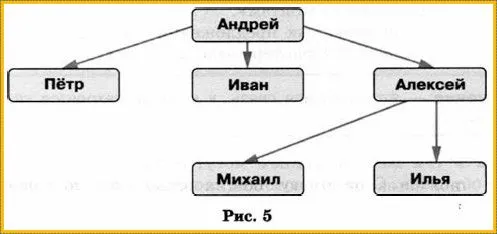
Такие отношения, как «должен быть сыном», «связан с железной дорогой», «покупает», «покупает», «покупает» и т.д., могут связывать только объекты определенного вида. Отношения «является элементом множества», «является частью множества» и «является видом» могут иметь любой вид объекта.
Отношения могут быть не только между двумя объектами, но и, например, между объектом и множеством объектов:
- Гарри Поттер — литературный персонаж;
- «Камчатка — это полуостров (является полуостровом)»;
- «Москва — столичный город».
Каждая из этих фраз описывает отношение «является элементом множества».
Отношения между множествами
Отношения могут связывать два множества объектов, напр:
- «файлы группируются в папки»;
- «колеса входят в состав автомобилей»;
- «бабочки — это насекомые ( являются разновидностью насекомых)».
Графически множества лучше всего изображать кругами, которые называются кругами Эйлера.
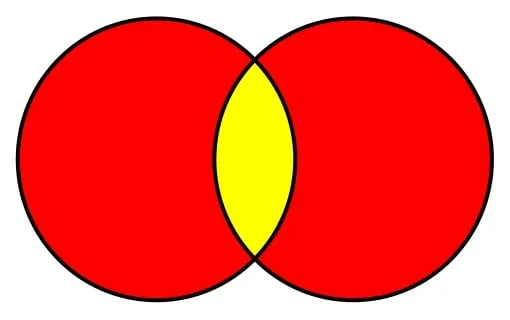
Если множества A и B имеют общие элементы, т.е. элементы, которые одновременно принадлежат и A, и B, то они называются пересекающимися (рис. 6).

Пример. Пусть A — множество электронных сообщений, а B — множество писем на русском языке. Все электронные письма на русском языке попадают в пересечение этих множеств.
Если у них нет общих элементов, они называются непересекающимися (рис. 7).
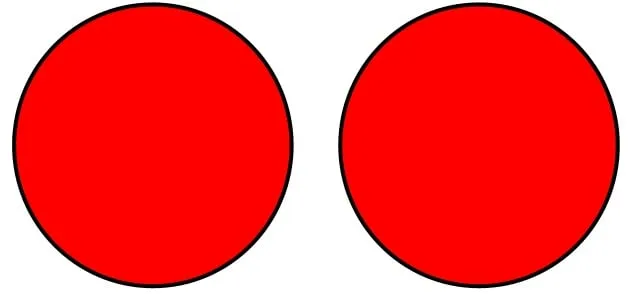
Пример. Пусть A — множество устройств ввода компьютера, B — множество устройств вывода. Эти множества не имеют общих элементов.
Если каждый элемент множества B является элементом множества A, то говорят, что B является подмножеством A (рис. 8).
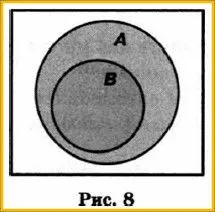
Пример. Пусть A — множество учеников, а B — множество учеников шестого класса. Множество учеников шестого класса является подмножеством множества учеников.
Если каждый элемент множества B является элементом множества A и, наоборот, каждый элемент множества A является элементом множества B, то говорят, что множества A и B равны (рис. 9).
Пример. Пусть A — множество равносторонних прямоугольников, а B — множество квадратов. Эти наборы равны.
Отношение «входит в состав»
В зависимости от ситуации объект может рассматриваться как множество или «разлагаться» на более мелкие объекты. Например, компьютер рассматривается как множество, когда вы хотите подсчитать количество компьютеров в школе. Чтобы получить представление о возможностях компьютера, нужно посмотреть на свойства его устройств, таких как процессор, память, жесткий диск и так далее.
Объект может состоять из множества идентичных (однородных, похожих) объектов. Например, объект «апельсин» состоит из нескольких частей — апельсиновых долек. Школьный класс» состоит из множества учеников — мальчиков и девочек примерно одного возраста. Каждый ученик является целостной, самостоятельной частью объекта «школьный класс».
Объект может состоять из множества различных объектов. Например, объект «компьютер» состоит из множества различных объектов (системный блок, монитор, клавиатура и т.д.). Если разделить объект «Компьютер» на части, то новые объекты получат разные имена; атрибуты новых объектов будут разными.
Когда мы описываем состав объектов, в одних случаях мы ссылаемся на состав конкретного объекта, а в других — на общие компоненты набора объектов. В последнем случае описание состава содержит ответ на вопрос «Из чего обычно состоят объекты данного множества?». Например:
- «в состав дома входят стены, крыша, двери, окна, …»;
- «в составе автомобиля есть двигатель, кузов, багажник, …».
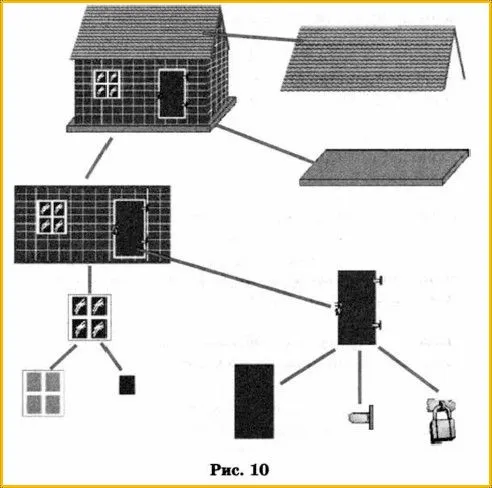
Описывая состав объекта, человек мысленно разбивает его на части. Обычно используется такой метод: сначала упоминается небольшое количество крупных частей, затем они разбиваются на более мелкие и так далее. Например, при описании дома хорошо сначала определить подвал, стены и крышу, затем поместить окно и дверь в стене, затем сказать, что окно состоит из рамы и стекла, и то же самое сделать для двери (рис. 10).
«Включение в состав» (диаграмма состава) отражает не только компоненты, но и порядок, в котором объект был «разобран». Поэтому он отражает структуру объекта. Линии без стрелок могут использоваться в диаграмме композиции, если имя объекта-компонента находится ниже имени объекта, которому принадлежит эта часть.
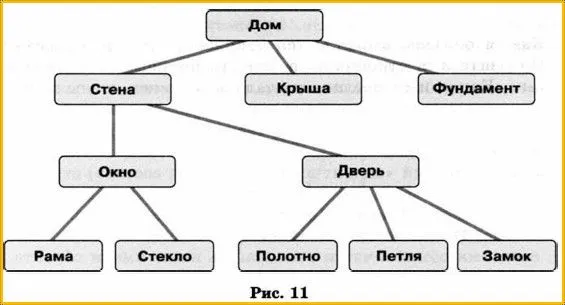
Все названия на рисунке 11 являются общими (они обозначают группы объектов), поскольку этот рисунок отражает состав не конкретного дома, а «дома вообще».
При описании характеристик сложного, составного объекта человек может назвать не только действия и характеристики всего объекта, но и действия и характеристики частей объекта. Например, весь дом можно построить и отремонтировать, покрасить крышу и установить стекло; весь дом имеет длину, ширину и высоту, стены имеют толщину, а крыша — высоту.
Объявление множеств
В математике скобки используются для обозначения множества, например, в Паскале, квадратные скобки используются, например, 1, 3, 5. Порядок элементов множества не важен. Поэтому наборы 3, 6, 9 и 9, 3, 6 идентичны.
Объявление переменной типа «набор» в виде набора данных сравнимо с объявлением одномерной таблицы:
var имя: set тип,Объявление переменной ch как набора с базовым типом char, например, будет выглядеть следующим образом
var ch: set char,Можно сначала объявить тип набора, а затем использовать его для объявления переменных:
type t_ch = set of char; var ch1, ch2: t_ch,Перечисления и диапазоны часто используются в качестве базовых типов:
type week_days = (Mon, Tue, Wed, Thu, Fri); var work_days: set week_days; var work_days: set week_days; var work_days: set 'A'...'Z',type nums = 5..25; var a: set nums,Объявление набора переменных не означает, что им присваивается набор значений.
Построение множества
Для отображения данных в наборе требуется оператор присваивания, в котором слева указывается имя переменной набора, а справа — выражение для набора или конструктора набора.
Конструктор ансамбля представляет собой список элементов, разделенных запятой в квадратных скобках. В качестве элементов можно использовать диапазоны значений:
type week_days = (Mon, Tue, Wed, Thu, Fri); var work_days: set week_days- lett: set 'A'...'Z'; begin work_days := Mon, Wed, Thu; lett := 'C', 'E'...'M', 'Z' end.Обратите внимание, что при задании множества порядок элементов не важен, а при задании диапазона — важен.
Множество, не содержащее элементов, называется пустым (или нулевым). В языке программирования Pascal он представлен квадратными скобками без элементов между ними:
Набор может быть объявлен как стандартная константа, для которой конструктор набора должен быть указан в описании после знака равенства. Например:
const lett: множество 'a'...'i' = 'a', 'e', 'i', 'o', 'y', 's', 'e', 'yu', 'i',Переменные также могут использоваться при построении множеств, при условии, что их текущие значения попадают в диапазон значений базового типа множества. Таким образом, если ch1 и ch2 — char, то допустима следующая последовательность утверждений:
ch1 := 'A', ch2 := 'K', chs := ch1, ch2, 'M',В результате получается набор ‘A’, ‘K’, ‘M’.
Вывод элементов множества
В Паскале элементы ансамбля не могут быть ни входными, ни выходными. Вы должны использовать вспомогательные переменные для организации их ввода/вывода. Однако вы можете использовать наборы в качестве элементов стандартных файлов.
type nums = 0..10; var a: набор чисел; i: Byte; begin a := 3, 0, 2; for i := 0 to 10 do if i in a then writeln(i); end.