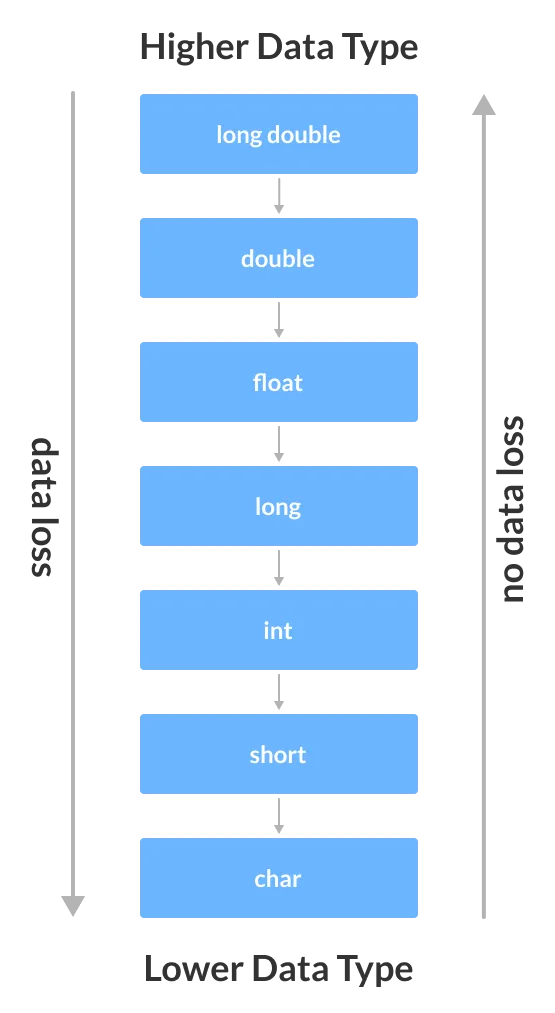
Его можно использовать для выявления фальшивых новостных аккаунтов или в террористических ячейках для изоляции лиц, которые могут передавать информацию остальной части графика.
Алгоритмы на графах. Алгоритмы нахождения кратчайшего пути
Этот алгоритм иногда называют алгоритмом Флойда-Уоршелла. Алгоритм Флойда-Уоршелла — это алгоритм работы с графами, разработанный Робертом Флойдом и Стивеном Уоршеллом в 1962 году. Он используется для поиска кратчайших путей между всеми парами узлов в графе.
Метод Флойда основан непосредственно на том факте, что в графе с положительным весом ребра, каждый неуложенный (содержащий более 1 ребра) кратчайший путь состоит из других кратчайших путей.
Этот алгоритм является более общим, чем алгоритм Дейкстры, поскольку он находит кратчайшие пути между любыми двумя точками графа.
Алгоритм Флойда использует матрицу A nxn, в которой вычисляются кратчайшие пути. Элемент Ai,j — это расстояние между точкой i и точкой j, которое имеет конечное значение, если существует ребро (i,j), и равно бесконечности в противном случае.
Алгоритм Флойда
Основная идея алгоритма. Пусть есть три вершины i, j, k и заданы расстояния между ними. Если выполняется неравенство Ai,k+Ak,j путь i->j путем i->k->j. Эта замена выполняется систематически во время выполнения алгоритма.
Шаг 0. Определяем начальную матрицу расстояний A0и матрица последовательности вершин S0. Каждый диагональный элемент двух матриц равен 0, что означает, что эти элементы не включены в расчет. Мы предполагаем, что k = 1.
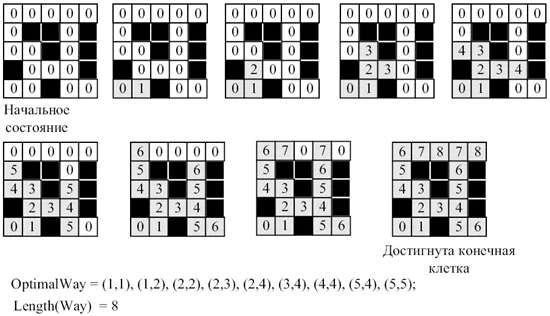
Мы определяем строку k и столбец k как верхнюю строку и верхний столбец. Мы предполагаем, что применяем описанную выше замену ко всем элементам Ai,j матрицы Ak-1. Если неравенство выполнено, выполните следующие действия:
- создаем матрицу Akпутем подстановки в таблицу Ak-1элемента Ai,j на сумму Ai,k+Ak,j ;
- создаем матрицу Skпутем подстановки в таблицу Sk-1элемента Si,j на k. Полагаем k = k + 1 и повторяем шаг k .
Таким образом, алгоритм Флойда выполняет n итераций, и после i-й итерации таблица A содержит длины кратчайших путей между любыми двумя парами вершин, при условии, что эти пути проходят через вершины от первой до i-й. На каждой итерации перечисляются все пары вершин, и путь между ними укорачивается на i-ю вершину (рис. 45.2).
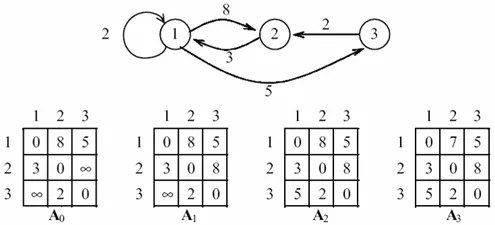
//Описание работы алгоритма Floyd void Floyd(int n, int **Graph, int **ShortestPath).
Обратите внимание, что для неориентированного графа все матрицы, полученные в результате преобразования, симметричны, поэтому достаточно вычислить только элементы над главной диагональю.
Когда граф представлен матрицей смежности, время выполнения этого алгоритма имеет порядок O(n 3 ), поскольку три круга вложены друг в друга.
Переборные алгоритмы
Алгоритмы, по сути, являются алгоритмами поиска, которые обычно ищут оптимальное решение. В этом случае решение выстраивается шаг за шагом. В этом случае обычно говорят о переборе вершин дерева вариантов. Вершины этого графа представляют собой промежуточные или конечные варианты, а ребра указывают пути построения вариантов.
Рассмотрим алгоритмы грубой силы, основанные на методах поиска графов, на примере задачи поиска кратчайшего пути в лабиринте.
Описание проблемы .
Лабиринт состоит из проходимых и непроходимых клеток и задается матрицей A размера mxn. Элемент матрицы Ai,j=0, если клетка (i,j) является проходной. В противном случае
Найдите длину кратчайшего пути от клетки (1, 1) до клетки (m, n).
Фактически, матрица смежности задана (с той разницей, что в ней нули заменены на бесконечности, а единицы — на нули). Лабиринт — это граф.
Вершинами вариационного дерева в этой задаче являются пути, начинающиеся из клетки (1, 1). Ребра указывают на построение этих путей и соединяют два пути длины k и k+1, где второй путь получается из первого путем добавления к нему еще одного пути.
Сломанная грубая сила
Этот метод основан на методе поиска по глубине. Тестирование методом «сломанной спины» считается методом проб и ошибок («попробуйте этот способ: если он не сработает, мы вернемся и попробуем другой способ»). Поскольку для поиска вариантов используется метод поиска в глубину, имеет смысл хранить текущий путь в дереве при запуске алгоритма. Этот путь является путевым стогом.
Вам также понадобится таблица Dist, размерность которой соответствует количеству узлов графа и в которой для каждого узла хранится расстояние до исходного узла.
Предположим, что поток представляет собой квадрат (в начале алгоритма это квадрат (1, 1)). Если у текущего квадрата есть соседний квадрат, который не находится в пути и еще не был посещен на этом пути, то сосед добавляется в путь, и сосед назначается текущему квадрату, в противном случае он удаляется из пути.
Из приведенного выше описания становится понятно, почему этот метод называется грубой силой с возвратом. Результатом является функция «извлечь из Way», которая уменьшает длину Way на 1.
Поиск заканчивается, когда путь пуст и предпринимается попытка возврата. В этом состоянии нет возврата (рис. 45.3).
Путь — это текущий путь, но ОптимальныйПуть также должен быть сохранен в процессе.
Улучшить алгоритм можно следующим образом: Длина Way не должна быть больше или равна длине OptimalWay. В этом случае найденный вариант, конечно, не является оптимальным. Это улучшение обычно означает, что как только становится известно, что текущий способ является неоптимальным, его необходимо изменить. Во многих случаях такое усовершенствование алгоритма может значительно сократить время поиска.
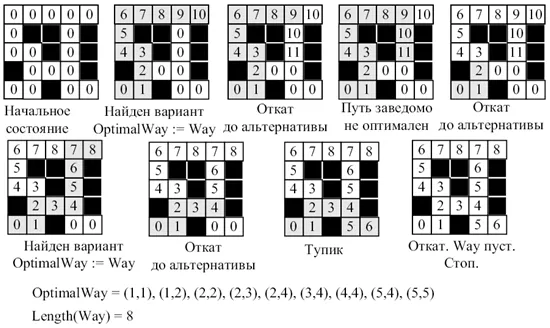
Рис. 45.3: Демонстрация алгоритма грубой силы с обратным перебором
/*Описание работы алгоритма перебора */ void Backtracking(int n, int m, int **Maze)
Волновой алгоритм
Ключевые термины
Алгоритм Дейкстры — это алгоритм поиска кратчайшего пути от одного узла графа до всех остальных узлов, и он работает только для графов без отрицательно взвешенных ребер.
Алгоритм Флойда — это алгоритм поиска кратчайшего пути между любыми двумя узлами графа.
Волновой алгоритм — это алгоритм грубой силы, основанный на поиске амплитуды и состоящий из двух шагов: Распространение волн и обратный путь.
Кратчайший путь — это путь в графе, т.е. последовательность узлов и ребер, которые встречают два соседних узла, и его длина равна .
Алгоритм грубой силы — это алгоритм обхода графа, основанный на последовательном поиске возможных путей.
Поиск в ширину — ПВШ (Breadth First Search — BFS)
Метод обхода графа, при котором сначала выполняется обход с первого узла, который мы еще не покинули (узлы хранятся в очереди). Обход в глубину, конечно, достигается путем рекурсивного обхода графа.
Последовательность обхода пиков при поиске диапазона
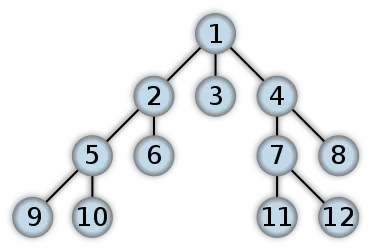
Поиск кратчайших путей в графах (объединение разделов по Дейкстре и Флойду)
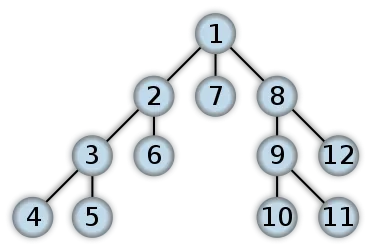
Алгоритм Дейкстры — это алгоритм для графов, который находит кратчайшее расстояние от одной из точек графа до всех остальных точек. Алгоритм работает только для графов без ребер с отрицательным весом (без ребер с отрицательной «длиной»).
Примеры для решения проблем
Вариант 1: Существует сеть дорог, соединяющая города. Некоторые дороги являются улицами с односторонним движением. Найти кратчайшие маршруты из заданного города в любой другой город (если путешествие возможно только по дорогам).
Вариант 2: Существует несколько рейсов между городами мира, для каждого из которых известна стоимость. Стоимость перелета из А в Б может отличаться от стоимости перелета из Б в А. Найдите самый дешевый маршрут (возможно, с пересадкой) из Копенгагена в Барнаул.
Идея алгоритма Дейкстры
Алгоритм состоит из 2 итерационных шагов:
- Добавление новой вершины («Расти» — GROW )
- «Релаксация», т.е. пересчёт расстояний до других вершин с учётом добавленной вершины ( RELAX ).
Более подробное описание:
Примечания:
Граф $G = (V,E)$, где $V$ — вершины, а $E$ — ребра.
$v_0$ — начальная вершина (от которой мы ищем кратчайшее расстояние до всех остальных).
$R_i$ — известное расстояние от вершины $v_0$ до вершины $i$.
$D$ — это множество вершин, от которых известно кратчайшее расстояние до $v_0$.
Граф $G=(V,E)$, где $V$ — вершины, а $E$ — ребра.
$v_0$ — начальная точка вершины
$R_i$ — кратчайшее расстояние от $v_0$ до $i$-й вершины.
Инициализация алгоритма:
$D = \$ — пустое множество.
$R_ = 0$ — расстояние от $v_0$ до $v_0$ = 0$.
$v = v_0$ — мы будем расти из вершины $v$.
Итерация (общий шаг алгоритма).
$GROW(V/D,v)$ — Добавляет вершину $v$ из множества $V/D$ в множество $D$.
$RELAX(V/D,v)$ — обходит достижимые вершины $v$, до которых мы еще не знаем кратчайшего расстояния, и обновляет расстояние $R_i$ от вершины $v$.
$v$ — вершина с минимальным $R$ из множества $V/D$.
Пока нам удается расти (операция $GROW$ добавляет вершину).
Алгоритм
Каждому узлу v из V присваивается значение av — минимальное известное расстояние этого узла от начальной точки s. Алгоритм работает пошагово — на каждом шаге исследуется один узел и делается попытка улучшить текущее расстояние до этого узла. Алгоритм завершается, когда все узлы посещены или когда вычислены расстояния до всех узлов, достижимых из начальной точки.
Инициализация. Значение начального узла принимается равным 0, значение остальных узлов — бесконечным (в программировании это реализуется присвоением большого значения, например, максимально возможного для данного типа). Это отражает тот факт, что расстояния от s до других узлов еще не известны.
Шаг алгоритма: Если все узлы были посещены, алгоритм завершается. В противном случае из еще не посещенных точек выбирается точка v с наименьшим расстоянием до исходной точки s и добавляется в список посещенных точек. Эта вершина находится с помощью перечисления всех непосещенных вершин. Он суммирует расстояние от исходной вершины u до непосещенной вершины v. На первом шаге s — единственная посещенная вершина, расстояние которой от начала координат (т.е. от самой себя) равно 0.
Алгоритм Флойда
Алгоритм Флойда-Уоршелла — это динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Он был разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом.
Предположим, что вершины графа пронумерованы от 1 до $n$, и введем обозначение $d_^k$ для длины кратчайшего пути из $i$ в $j$, который, кроме самих вершин $i,\;j$, проходит только через вершины 400 \ldots k$. Очевидно, что $d_^$ — это длина (вес) ребра $(i,\;j)$, если оно существует (иначе его длину можно назвать $\infty$).
Существует две версии $d_^,\;k\ в \mathbb(1,\;\ldots,\;n)$:
- Кратчайший путь между $i,\;j$ не проходит через вершину $k$, тогда $d_^=d_^$
- Существует более короткий путь между $i,\;j$, проходящий через $k$, тогда он сначала идёт от $i$ до $k$, а потом от $k$ до $j$. В этом случае, очевидно, $d_^=d_^ + d_^$
Таким образом, чтобы найти значение функции, достаточно выбрать минимум из двух заданных значений.
$d_^0$ — длина ребра $(i,\;j)$.
Алгоритм Флойда-Уоршелла последовательно вычисляет все значения $d_^$, $\ для всех i,\; j$ для $k$ от 1 до $n$. Полученные значения $d_^$ являются длинами кратчайших путей между узлами $i,\; j$.
для k := от 1 до nfor i := 1 to n do<из i-ой вершины>для j := от 1 до n<в j-ую вершину>Wij = min(Wij, Wik + Wkj),
import sys.stdin = open('floyd.in') sys.stdout = open('floyd.out', 'w') # чтение входных данных n = int(input()) # n - количество вершин a = for i in range(n): # выполнить n строк a. append(int(x) for x in input().split()) for i in range(n): for j in range(n): if aij == -1: aij = float('inf') for k in range(n): for i in range(n): for j in range(n): if aik + akjmax: max = aij print(max)
Двухэтапные алгоритмы
К сожалению, двунаправленный алгоритм Дейкстры работает только в два раза быстрее обычного алгоритма, который является очень медленным. Рассмотрим двухшаговый алгоритм поиска кратчайшего пути:
- Препроцессинг:
- запускается единожды для графа,
- может занимать много времени,
- рассчитывает некую вспомогательную информацию.
- Запрос:
- может использовать данные, полученные во время препроцессинга,
- запускается по требованию для пары math(s,t)/math ,
- должен выполняться очень быстро (в реальном времени).
В этой связи можно рассмотреть два примера:
- Алгоритм Дейкстры: препроцессинг — ничего не делать, запрос — выполнение алгоритма Дейкстры;
- Полный перебор: препроцессинг — посчитать таблицу расстояний размером mathn \times n/math (займёт порядка 5 лет времени и 1 петабайта памяти для карты Европы), запрос — обратиться к элементу таблицы.
Эти два примера являются крайними случаями. Нам нужно что-то более гибкое: предварительная обработка за часы/минуты, линейное увеличение объема предварительно вычисленных данных с ростом размера графа и запросы в реальном времени.
ALT
ALT означает A* + L andmarks + T riangle inequality : A* + Landmarks + Triangle inequality.
- Препроцессинг:
- взять небольшое количество вершин (например, 16), обозначив их как ориентиры (англ. landmarks ),
- для каждого из ориентиров посчитать кратчайшие пути до всех вершин,
- сохранить эти пути.
- Запрос:
- используем A*,
- если некоторое ребро находится на кратчайшем пути между исходной точкой и ориентиром — по нему идём в первую очередь.
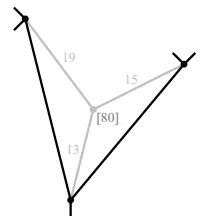
Воспользуемся неравенством треугольника для оценки нижнего пути (см. рис. 1). Тогда пусть mathA/math будет одним из ориентиров:
- mathdist(v,w)\geqslant dist(A,w)-dist(A,v)/math ,
- mathdist(v,w)\geqslant dist(v,A)-dist(w,A)/math ,
- mathdist(v,w)\geqslant \max\/math .
Этот эвристический метод хорошо работает для графов путей, для которых справедливо следующее: кратчайший путь обычно проходит через небольшое количество местных дорог, затем через главную дорогу и снова через несколько местных дорог.
Трудности при выборе ориентиров:
- хороший ориентир для запроса maths \rightsquigarrow t/math должен находиться «до» maths/math (точно не будет общих рёбер на кратчайшем пути) или «за» matht/math (чем острее угол, тем меньше отклонение от предварительно посчитанного кратчайшего пути до искомого),
- нам нужно выбрать такие ориентиры, которые будут неплохими для всех запросов.
Представляется разумным выбирать ориентиры на краю дорожной сети, поскольку там больше крутых поворотов и ориентиры лучше.
Существует несколько алгоритмов выбора ориентиров:
Случайный выбор (random)
Как следует из названия, ориентиры выбираются случайным образом.
Плоскостной (planar)
- Разделим карту на mathk/math секторов одинаковой площади,
- возьмём ориентиром наиболее удалённую точку от центра в каждом секторе.
Итог
Сравнение различных эвристик для поиска кратчайшего пути на карте США| Как следует из названия, ориентиры выбираются случайным образом. Метод подразумевает. | Время предварительной обработки, м | Память для предварительной обработки, МБ | Пики, отсканированные с приложения, мкм, МБ (как следует из термина). | Время поиска, мс |
|---|---|---|---|---|
| Алгоритм Дейкстры | — | 536 | 11 808 864 | 5440,5 |
| ALT(16 целей) | 18 | 2563 | 187 968 | 295,45 |
| Достичь | 28 | 893 | 2 405 | 1,77 |
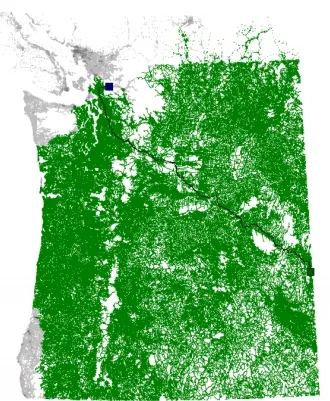
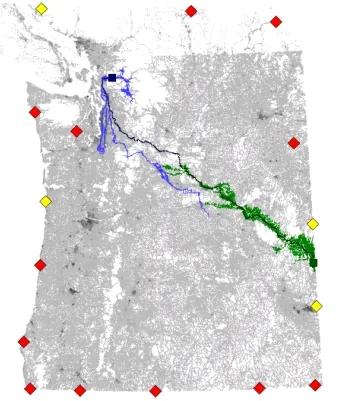
| Алгоритм Дейкстры | АЛТ (16 рекомендаций) | Достичь |
|---|---|---|
 |
 |
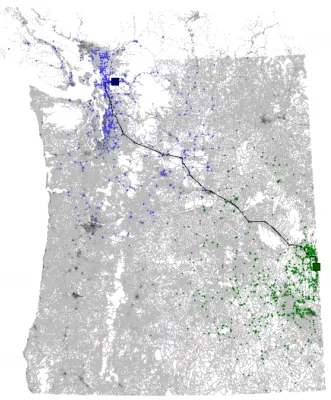 |
- зелёный квадрат — начало пути
- синий квадрат — конец пути
- зелёные линии — пути, пройденные прямым обходом
- синие линии — пути, пройденные обратным обходом
- красные ромбы — ориентиры
- жёлтые ромбы — выбранные при поиске пути ориентиры