Гамильтоновы графы. Гамильтонов цикл в графе.

Содержание

Гамильтонов путь или доказуемый путь — это путь, который посещает каждый узел графа ровно один раз. Граф, содержащий гамильтонов путь, называется доказуемым графом. Граф является гамильтоновым связным, если для каждой пары вершин существует гамильтонов путь между этими двумя вершинами.

Поиск гамильтоновых циклов и цепей в кубических графах

Царьков, В. В. Поиск гамильтоновых петель и цепей в кубических графах / В. В. Царьков. В. Царьков. — Текст : прямой // Молодой ученый — 2009 — № 12 (12) — С. 9-12. — URL: https://moluch.ru/archive/12/886/ (accessed 26.11.2022).

Введение. Задачи на графах находят применение в различных областях, связанных с широким спектром математических методов анализа происходящих в них процессов. В настоящее время в научной и учебной литературе описаны и представлены эффективные методы и алгоритмы решения таких задач. Были разработаны пакеты прикладного программного обеспечения для решения ряда стандартных задач, например, задач покрытия графов, раскраски графов, изоморфизма графов. Применение этих пакетов логично, оправданно и вполне возможно без знания алгоритмов, используемых для решения задач, и технологий, позволяющих реализовать эти алгоритмы. В то же время теоретические исследования позволяют совершенствовать и более эффективно использовать разработанные пакеты.

В связи с этим целью данной работы является разработка комбинированного подхода к решению графовых задач с использованием как численных схем и методов, так и теоретических тезисов. Мы изучаем гамильтониан неориентированных кубических графов, которые представляют собой объединение двух окружностей длины n и соединяющих их боковых ребер. Формулируются гипотезы о существовании гамильтоновой окружности в данном кубическом графе. Мы приводим описание и результаты вычислительного алгоритма для проверки сформулированных гипотез. 1.

Основные определения. Граф G — это пара (V(G),E(G)), где V(G) — непустое конечное множество элементов, называемых узлами, а E(G) — конечное семейство неупорядоченных пар элементов из V(G) (которые не обязательно различны), называемых ребрами,
Обозначим через

если существует ребро, соединяющее вершину,

в других случаях,

Путь в графе G — это конечная последовательность ребер вида … такая, что
Путь называется цепью, если все его ребра дискретны, и простой цепью, если все его вершины дискретны. Цепь или простая цепь является замкнутой, если

Окружность, которая проходит через каждую вершину один раз, называется гамильтонианом. Граф, содержащий такую окружность, называется гамильтоновым графом.

Пусть G — конечная группа S G\, тогда

G( G, S) — граф Кейли

V(G)= G — множество вершин

E(G)=

2. условия существования гамильтоновой окружности на графе. Мы формулируем без доказательства достаточные условия существования гамильтоновой окружности в n-вертикальном неориентированном графе 8, 10.

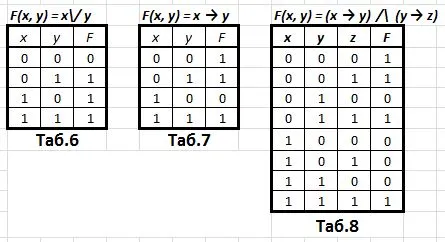
Теорема Оре. Если несмежные вершины удовлетворяют условию — степень вершин.

Теорема Дирака: Если, то условие

Под кубическим графом мы понимаем граф, в котором степень каждой вершины равна трем.

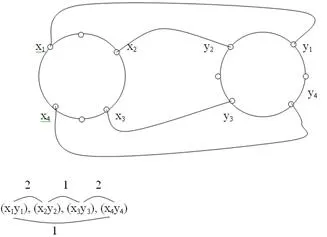
Обозначим кубические графы, возникающие из двух окружностей одинаковой длины, соединенных боковыми ребрами, через, и .

На рисунке 1.2 показан кубический неориентированный граф с 8 вершинами и соответствующая матрица смежности.

Можно доказать истинность следующего утверждения:

Лемма В графе существует гамильтонова окружность с двумя боковыми ребрами тогда и только тогда, когда существуют два боковых ребра, соединяющие соседние вершины по долям.

Задача о коммивояжере

Рассмотрим алгоритм поиска гамильтонова цикла в примере задачи о коммивояжере.

Описание задачи

Проблема:

Задача о коммивояжере (TSP) — это задача, в которой коммивояжер должен посетить N /math городов, посетив каждый из них ровно один раз и закончив свое путешествие в городе, из которого он начал. В каком порядке он должен посетить города, чтобы общая продолжительность путешествия была как можно меньше?

Варианты решения

Задача о путешествующем продавце относится к классу NP-полных задач. Рассмотрим два варианта решения с экспоненциальным временем работы.

Поиск конверсий

Вы можете решить эту проблему путем перебора всех перестановок. Для этого нужно сгенерировать все math N! /math возможных перестановок вершин исходного графа, вычислить длину пути для каждой перестановки и выбрать наименьшую из них. Но тогда проблема не разрешима даже для достаточно малых mathN/math. Сложность алгоритма mathO(\times)/math .

Динамическое программирование с подмножествами (с масками)

Комбинаторная задача состоит в том, чтобы найти кратчайший гамильтонов цикл в графе. Мы определяем начальный узел maths/math и ищем гамильтонов цикл с наименьшей стоимостью — путь от maths/math к maths/math, который проходит через все узлы (кроме начального узла) один раз. Поскольку искомый цикл проходит через каждую вершину, выбор математики не имеет значения. Поэтому мы полагаем, что maths = 0 /math .

Подмножества вершин кодируются в виде битовых векторов, где mathmask_i/math указывает значение бита mathi/math в векторе mathmask/math.

Пусть mathdimask/math обозначает минимальную стоимость пути из вершины mathi/math в вершину math0/math, который (исключая вершину mathi/math ) проходит один раз через все и только те вершины mathj/math, для которых mathmask_j = 1/math (т.е. mathdimask/math уже является оптимальным путем из mathi/math в math0/math, который проходит через вершины, для которых mathmask_j = 1/math. Если mathmask_j = 0/math, то эти вершины еще не были посещены).

Алгоритм циклического поиска имеет следующий вид:

Начальное состояние — когда находимся в math0/math -й вершине, ни одна вершина не посещена, а пройденный путь равен math0/math (т.е. mathi = 0/math и mathmask = 0/math ).
Для остальных состояний ( mathi \ne 0/math или mathmask \ne 0/math ) перебираем все возможные переходы в mathi/math -ую вершину из любой посещенной ранее и выбираем минимальный результат.
Если возможные переходы отсутствуют, решения для данной подзадачи не существует (обозначим ответ для такой подзадачи как math\infty/math ).

Стоимость минимального гамильтонова круга на исходном графе равна math d02^n-1/math — стоимости пути от math0/math — вершины до math0/math — вершины, когда мы должны посетить все вершины. Это решение требует mathO(\times)/math памяти и mathO(\times)/math времени.

Для восстановления самого пути используется соотношение math dimask = w(i, j) + djmask — 2^j /math, которое выполняется для всех вершин, входящих в минимальный цикл. Мы начинаем с состояния math i = 0 /math, math mask = 2^n — 1 /math, находим вершину mathj/math, для которой выполняется вышеуказанное соотношение, добавляем mathj/math к ответу, пересчитываем текущее состояние как mathi = j/math, math mask = mask — 2^j /math. Процесс заканчивается состоянием mathi = 0/math, math mask = 0 /math .

См. также

Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом «ЛИБРОКОМ», 2009. — 60 с.
Седжвик Р. Фундаментальные алгоритмы на C++. Алгоритмы на графах. — СПб: ООО «ДиаСофтЮП», 2002.
Гамильтонов граф
Задача коммивояжера в русской википедии
Задача коммивояжера в немецкой википедии
Романовский И. В. Дискретный анализ. СПб.: Невский Диалект; БХВ-Петербург, 2003. ISBN 5-7940-0114-3
Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом «Вильямс», 2005. ISBN 5-8459-0857-4

Алгоритмы и структуры данных
Обходы графов
Гамильтоновы графы
Дискретная математика и алгоритмы
Динамическое программирование
Классические задачи динамического программирования

Суперпозиция

Первым шагом в большинстве квантовых алгоритмов является генерация суперпозиции всех входных кубитов. Однако здесь мы можем отойти от традиции и использовать небольшой трюк, который применили авторы данной статьи. Суть трюка заключается в следующем: если нам известны слабые комбинации кубитов, мы можем заранее исключить их из суперпозиции.

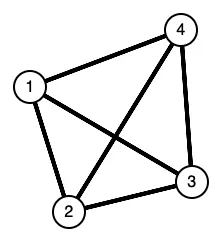
Поскольку 1-й шаг выполняется из точки O и первая вершина должна быть соединена с этой точкой, это не может быть вершина A, а только вершины B, C или D. Аналогично, последний, 5-й шаг выполняется из 4-й вершины в точку O и должен быть соединен с точкой O, поэтому он не может быть вершиной A.

Поскольку первой вершиной может быть только вершина B, C или D, первая пара кубиков, соответствующая первой вершине пути, может принимать только следующие значения: 01, 10 и 11. То же самое относится и к последней паре кубиков, соответствующей четвертой вершине пути.

Таким образом, мы исключаем из суперпозиции избыточную комбинацию 00 (вершина A) для первой и четвертой вершин, а значит, не нужно проверять связь этих вершин с неподвижной точкой O и сокращаем количество комбинаций до 3 * 4 * 4 * 3 = 144.

Итак, давайте посмотрим, как эта техника работает для пары кубитов.

Начальное состояние системы из двух кубитов описывается следующим образом:

Выполним ряд преобразований.

Шаг 1: Применим к первому qbite оператор

под таким углом, что матрица операторов принимает следующий вид:

Мы не будем искать «красивое» значение угла и устанавливать его равным:

Рассмотрим, как этот оператор действует на первый кубит:

После воздействия оператора на первый кубит пары, мы получаем следующую суперпозицию двух кубитов:

Шаг 2: Действуем на втором кубите с помощью управляемого клапана Adamar.

Управляемые ворота Хадамарда изменяют второй гобит только в том случае, если первый гобит тот же самый

Шаг 3: Примените $NOT$ ко второму кубиту

Затвор NOT применяется ко второму кубиту:

Таким образом, это суперпозиция, которая не содержит комбинации 00.

Теперь, когда мы подробно объяснили теоретическую часть, мы можем приступить к написанию соответствующей процедуры. Библиотека qiskit имеет все ворота, упомянутые в теоретической части:

Однокубитный вентиль — QuantumCirquit. ry (theta, target_qubit)
- theta — угол
- target_qubit — кубит, на который воздействует вентиль
- control_qubit — контролирующий кубит
- target_qubit — кубит, на который воздействует вентиль
- target_qubit — кубит, на который воздействует вентиль
Давайте напишем процедуру, которая вставляет пару кубитов и применяет к ним, один за другим, все операторы, упомянутые в теоретической части:
```
import numpy as np theta = 2 * np.arccos(1 / np.sqrt(3)) def exclude_00(qc, pair, reverse=False): if not reverse: qc.ry(theta, pair0) qc.ch(pair0, pair1) qc.x(pair1) qc.x(pair1) else: qc.x(pair1) qc.ch(pair0, pair1) qc.ry(-theta, pair0)
```
Сразу отмечу, что должен быть возможен обратный ход этого процесса, поэтому мы ввели дополнительный аргумент обратного хода. Более подробно о необходимости этого я расскажу позже.

Оператор диффузии Гровера в матричном выражении представляет собой обычную единичную матрицу, где все диагональные элементы равн ы-1, за исключением левого верхнего элемента, который равен 1. Оператор инвертирует фазу любого вектора, кроме вектора .

Пример оператора, действующего на вектор:

Пример оператора, действующего на любой другой вектор:

Нет необходимости «строить» конфигурацию ворот для диффузионного оператора, она уже разработана. Для набора из n кубиков оператор имеет следующий вид:

Теперь мы хотим написать функцию, выражающую оператор диффузии Гровера. Функция является глобальной и принимает на вход любое количество кубитов.
```
def diffusion(qc, qubits): qc.h(qubits) qc.x(qubits) qc.h(qubits-1) length = len(qubits) if length>3: qc.mct(qubits0:-1, qubits-1) elif length == 3: qc.toffoli(qubits0:-1, qubits2) elif length == 2: qc.cx(qubits0, qubits1) qc.h(qubits-1) qc.x(qubits)
```
Одни из трех ворот используются в качестве центрального элемента привода:
- когда на вход поступают всего 2 кубита — простой вентиль CNOT
- когда 3 кубита — вентиль Тоффоли
- когда 4 и более кубита — вентиль Тоффоли для многих кубит
Улучшение оператора диффузии Гровера

Поскольку мы не везде использовали однокбитовые ворота Адамара для создания начальной суперпозиции входных кубитов, нам необходимо изменить оператор диффузии.

В своей первоначальной форме оператор диффузии Гровера применяет ворота Хадамарда ко всем входным кубитам на входе, возвращая кубиты из суперпозиции в обычное несвязанное состояние. На выходе оператор снова применяет ворота Хадамарда для создания суперпозиции.

Однако при генерации суперпозиции мы применили специальные операторы для устранения избыточных комбинаций из первой и четвертой пар кубитов и применили ворота Хадамарда только ко второй и третьей парам кубитов.

Аналогично, мы отключили входные и выходные ворота Адамара в операторе диффузии Гровера для нашего алгоритма:
```
def diffusion(qc, qubits): # qc.h(qubits) qc.x(qubits) qc.h(qubits-1) length = len(qubits) if length>3: qc.mct(qubits0:-1, qubits-1) elif length == 3: qc.toffoli(qubits0:-1, qubits2) elif length == 2: qc.cx(qubits0, qubits1) qc.h(qubits-1) qc.x(qubits)
```
Теперь это выглядит следующим образом:

И прежде чем вызвать оператор, мы применяем обратную операцию создания наложения, а затем снова создаем наложение:
```
exclude_00(qc, qr0:2, reverse=True) qc.h(qr2:6) exclude_00(qc, qr6:8, reverse=True) diffusion(qc, qr0:8) exclude_00(qc, qr0:2) qc.h(qr2:6) exclude_00(qc, qr6:8)
```
На этом этапе полезно использовать обратную версию процедуры исключения комбинации 00 из наложения.

Собираем все вместе

Мы не будем подробно описывать принципы работы алгоритма Гровера с его обучающими примерами. Если n — это количество входных кубиков для оракула, в нашем случае 8, то количество итераций алгоритма Гровера должно быть следующим:

То есть, нам нужно всего 2 итерации алгоритма, чтобы получить дискретный результат.

5.1. Общая схема

Мы рассмотрели все элементы алгоритма и теперь хотим начать объединять элементы в единый круг функций. Общая схема выглядит следующим образом:

Скачайте и установите библиотеки Qiskit, NumPy и Matplotlib для Python.
```
>Pip3 install qiskit qiskit numpy matplotlib
```
Импортируйте необходимые библиотеки.
```
import numpy as np from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit, Aer, execute
```
Заранее подготовьте процедуру поиска совпадения вершин.
```
def find_equality(. ): # см. код выше
```
Подготовьте необходимые нам переменные и вспомогательные функции:
```
имена_вершин =.<'A': '00', 'B': '01', 'C': '10', 'D': '11',>ссылки = ссылки.<'A': 'C','D', 'B': 'C','D', 'C': 'A','B','D', 'D': 'A','B','C',>вершина_к_11 = вершина_к_11
```
Подготовьте процедуру для нахождения несвязных вершин и оператора диффузии.
```
def find_disconnection(. ): # См. приведенный выше код процедуры find_disconnection def diffusion(. ): # См. приведенный выше код процедуры диффузии.
```
Подготовьте процедуру для удаления лишних вершин из наложения:
```
theta = 2 * np.arccos(1 / np.sqrt(3)) def exclude_00(qc, pair, reverse=False): if not reverse: qc.ry(theta, pair0) qc.ch(pair0, pair1) qc.x(pair1) else: qc.x(pair1) qc.ch(pair0, pair1) qc.ry(-theta, pair0)
```
Теперь мы должны решить, сколько локтей нам нужно в общей сложности:

Характеристики

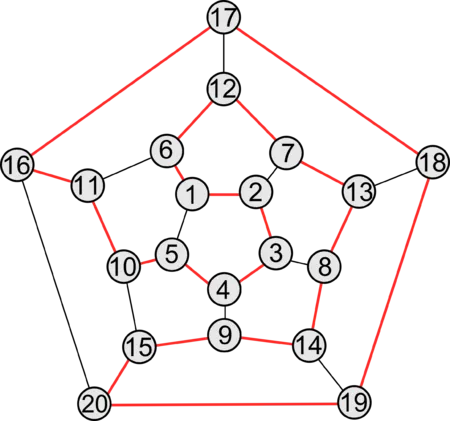
Граф Гершеля — это наименьший возможный многогранный граф без гамильтонова круга. Показан возможный путь гамильтониана.

Любой гамильтонов круг может быть преобразован в гамильтонов путь путем удаления одного из его ребер, но гамильтонов путь может быть расширен до гамильтонова, только если его ребра являются смежными.

Все гамильтоновы графы являются бимодальными, но бимодальный граф не обязательно должен быть гамильтоновым (см., например, граф Петерсена) 6

Эйлеров граф (а связный граф, в котором каждая вершина имеет четную степень) обязательно имеет Эйлеров тур — замкнутый обход, который проходит по каждому ребру графа ровно один раз. Этот тур соответствует гамильтоновой окружности в линейном графе L ( gram ), так что линейный граф любого эйлерова графа является гамильтоновым. Линейные графы могут иметь другие гамильтоновы циклы, которые не соответствуют эйлеровым циклам, и, в частности, линейный граф L ( gram ) любого гамильтонова графа сам является гамильтоновым, независимо от того, является ли этот граф эйлеровым. 7

А турнир (с более чем двумя вершинами) является гамильтоновым тогда и только тогда, когда он сильно связен.

Число отдельных гамильтоновых циклов в полном неориентированном графе с n вершинами ( n — 1)! / 2 и в полном направленном графе с n вершинами ( n — 1)! В этих измерениях предполагается, что циклы, идентичные за исключением начальной точки, не учитываются отдельно.

Теорема (Уитни, 1931) Плоская триангуляция с четырьмя связями имеет гамильтонов круг. Теорема (Тутте, 1956) Квадратичный связный планарный граф имеет гамильтонов круг.

Алгебраическим представлением гамильтоновых кругов соответствующего взвешенного планарного графа (дуги которого имеют связанные веса из определенного главного поля) является полином гамильтониана взвешенной матрицы смежности, определяемый как сумма весов дуг гамильтоновых кругов графа. Этот полином неидентичен нулю как функция весов дуг только в том случае, если орграф является гамильтоновым. Связь между трудностями в расчетах и вычислением константы была показана в работе Kogan (1996).
- Гипотеза Барнетта, открытая проблема гамильтоничности кубической двудольныймногогранные графы
- Эйлеров путь, путь через все ребра графа
- Теорема Флейшнера, на гамильтониане квадраты графиков
- Код Грея
- Теорема Гринберга давая необходимое условие для планарные графы иметь гамильтонов цикл
- Гамильтонова проблема пути, вычислительная задача нахождения гамильтоновых путей
- Гипогамильтонов граф, негамильтонов граф, в котором каждый подграф с удаленными вершинами является гамильтоновым
- Рыцарский тур, гамильтонов цикл в граф рыцаря
- Обозначение LCF для гамильтониана кубические графы.
- Гипотеза Ловаса который вершинно-транзитивные графы гамильтоновы
- Панциклический граф, графы с циклами любой длины, включая гамильтонов цикл
- Семь мостов Кенигсберга
- Показатель краткости, численная мера того, насколько далеко от гамильтониана могут быть графы в семействе
- Змея в коробке, самый длинный индуцированный путь в гиперкубе
- Алгоритм Штейнхауса – Джонсона – Троттера найти гамильтонов путь в пермутоэдр
- Субгамильтонов граф, подграф планарный Гамильтонов граф
- Гипотеза Тэйта (теперь известно ложь), что 3-регулярный многогранные графы гамильтоновы
- Проблема коммивояжера
Примечания
1. ^ Биггс, Н. Л. (1981), «Т. П. Киркман, математик», Бюллетень Лондонского математического общества, 13 (2): 97–120, Дои:10.1112 / blms / 13.2.97, МИСТЕР0608093 .
2. ^ Уоткинс, Джон Дж. (2004), «Глава 2: Рыцарские туры», Через доску: математика задач на шахматной доске, Princeton University Press, стр. 25–38, ISBN978-0-691-15498-5
3. .
4. ^ де Руйтер, Йохан (2017). Лабиринты Гамильтона — Руководство для новичков .
5. ^ Фридман, Эрих (2009). «Гамильтоновы лабиринты». Дворец головоломок Эриха. В архиве из оригинала 16 апреля 2016 г.. Получено 27 мая 2017 .
6. ^ Гарднер, М. «Математические игры: о поразительном сходстве между икосианской игрой и башнями Ханоя». Sci. Амер. 196, 150–156, май 1957 г.
7. ^ Эрик Вайнштейн. «Двусвязный граф». Wolfram MathWorld.
8. ^ Балакришнан, Р .; Ранганатан, К. (2012), «Следствие 6.5.5», Учебник теории графов, Springer, стр. 134, ISBN9781461445296
9. .
10. ^ Гулд, Рональд Дж. (8 июля 2002 г.). «Успехи в гамильтоновой проблеме — обзор» (PDF). Университет Эмори. Получено 2012-12-10 .
11. ^ Rahman, M. S .; Кайкобад, М. (апрель 2005 г.). «О гамильтоновых циклах и гамильтоновых путях». Письма об обработке информации. 94 : 37–41. Дои:10.1016 / j.ipl.2004.12.002.
12. ^ Moon, J .; Мозер, Л. (1963), «О гамильтоновых двудольных графах», Израильский математический журнал, 1 (3): 163–165, Дои:10.1007 / BF02759704, МИСТЕР0161332
- Берже, Клод; Гуила-Хоуири, А. (1962), Программирование, игры и транспортные сети, Нью-Йорк: Sons, Inc.
- ДеЛеон, Мелисса (2000), «Исследование достаточных условий для гамильтоновых циклов» (PDF), Журнал бакалавриата по математике Роуз-Халман, 1 (1), заархивировано из оригинал (PDF) на 2012-12-22, получено 2005-11-28
- .
- Дирак, Г.А. (1952), «Некоторые теоремы об абстрактных графах», Труды Лондонского математического общества, 3-я сер., 2 : 69–81, Дои:10.1112 / плмс / с3-2.1.69, МИСТЕР0047308
- .
- Гамильтон, Уильям Роуэн (1856 г.), «Меморандум о новой системе корней единства», Философский журнал, 12 : 446
- .
- Гамильтон, Уильям Роуэн (1858 г.), «Счет икосианского исчисления», Труды Королевской ирландской академии, 6 : 415–416
- .
- Мейниэль, М. (1973), «Непредусмотренное условие существования системы Hamiltonien dans un graphe orienté», Журнал комбинаторной теории, Серия B, 14 (2): 137–147, Дои: 10.1016/0095-8956(73)90057-9, МИСТЕР0317997
- .
- Руда, Эйстейн (1960), «Заметка о схемах Гамильтона», Американский математический ежемесячник, 67 (1): 55, Дои:10.2307/2308928, JSTOR2308928, МИСТЕР0118683
- .
- Поса, Л. (1962), «Теорема о линиях Гамильтона», Мадьяр Туд. Акад. Мат. Kutató Int. Közl., 7 : 225–226, МИСТЕР0184876
- .
- Уитни, Хасслер (1931), «Теорема о графах», Анналы математики, Вторая серия, 32 (2): 378–390, Дои:10.2307/1968197, JSTOR1968197, МИСТЕР1503003
- .
- Тутте, В. Т. (1956), «Теорема о плоских графах», Пер. Амер. Математика. Soc., 82 : 99–116, Дои: 10.1090 / с0002-9947-1956-0081471-8
- .
- Коган, Григорий (1996), «Вычисление перманентов над полями характеристики 3: где и почему становится сложно», 37-й ежегодный симпозиум по основам компьютерных наук (FOCS ’96) : 108–114, Дои:10.1109 / SFCS.1996.548469, ISBN0-8186-7594-2

Гамильтоновы графы. Гамильтонов цикл в графе.

Поиск гамильтоновых циклов и цепей в кубических графах

Похожие статьи

Графы в Scilab | Статья в сборнике международной научной.

Теорема Дирака

Теорема Оре

Теорема Поша

Теорема Редеи-Камиона

Теорема Гуйя-Ури

Теорема Хватала

Задача о коммивояжере

Описание задачи

Варианты решения

Поиск конверсий

Динамическое программирование с подмножествами (с масками)

См. также

Суперпозиция

Собираем все вместе

5.1. Общая схема

Характеристики

Примечания