Это статья для расширения кругозора и общих математических знаний. Программисты, которые знают, как работает математика, могут написать более элегантный код, чем те, кто не знает. Мы хотим, чтобы вы писали хороший код и зарабатывали много денег.
Какие системы счисления называются непозиционными
В вычислительной технике используются как методы записи чисел с местами, так и методы записи чисел без мест. В позиционном методе числа представляются в определенном порядке, чтобы получить значение числа.
Непозиционная нотация — это способ записи чисел с помощью символов, при котором изменение положения символов не влияет на значение числа.
Разновидности непозиционных систем счисления с примерами
Существует несколько типов непозиционной нотации.
Предупреждение. Если учитель узнает, что ваша работа является плагиатом, у вас могут возникнуть серьезные неприятности (вплоть до исключения из школы). Если вы не в состоянии написать работу самостоятельно, закажите ее здесь.
Биномиальная
В этом методе для записи чисел используются биномиальные коэффициенты.
Биномиальные коэффициенты представляют собой сумму числа комбинаций, определенных только для неотрицательных целых чисел. Такие обобщения часто встречаются в задачах, где необходимо проверить все возможные ответы, а также в теории вероятностей.
Число x в рассматриваемой системе является суммой биномиальных коэффициентов:
Биномиальными числами являются:
- линейные – в виде последовательности 0 и 1. Эта форма предполагает наличие двух чисел: количество столбцов в матрице и сумму числа столбцов и строк в матрице;
- матричные – в виде матрицы, элементами которой являются единицы и нули. При этом в одном столбце матрицы возможно наличие только одной 1.
Пример преобразования матричной формы в линейную:
Каждый компонент матрицы соответствует биномиальному коэффициенту. Сложение коэффициентов, соответствующих единицам матрицы, дает количественный эквивалент.
Применение биномиальных чисел:
- действия с комбинаторных кодом – их получение, перебор и нумерация;
- шифрование информации и сжатие данных благодаря двоичному алфавиту данной системы счисления;
- представление решений генетических алгоритмов.
Греческая
Греческая система счисления — это способ представления числа с помощью букв греческого алфавита и определенных префиксов. Другие названия этого метода — ионный, неоэллинский.
В Греции алфавитная запись чисел началась в 3 веке до нашей эры. Буквы греческого алфавита соответствуют следующим числам:
Система Ionic может записывать только числа от 1 до 999.
Римская
Латинская система нумерации — это метод записи чисел с использованием символов латинского алфавита.
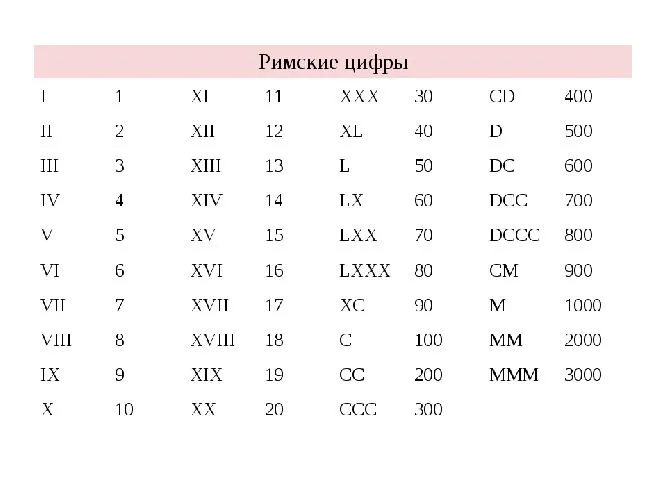
Буквы римского алфавита соответствуют числовому значению:
- I — один;
- V — пять;
- X — десять;
- L — пятьдесят;
- C — сто;
- D — пятьсот;
- M — тысяча.
Для представления десятичных чисел с помощью латинских букв действуют следующие правила:
- Стоящий слева от большего меньший символ вычитается из большего.
- Стоящий справа от большего меньший символ прибавляется к большему.
Если перевести число 67 в латинскую систему счисления, то получится следующая последовательность латинских букв: LXVII = (50 + 10) + (5 + 2) = 60 + 7.
545 — это DXLV = 500 + (50 — 10) + 5.
Применение этой системы счисления:
- обозначение знаменательных дат;
- разделов и глав книг;
- обозначение порядкового номера.
Древнеегипетская
Способ записи чисел в Древнем Египте был основан на иероглифах. Эти символы использовались для записи основных чисел 1, 10, 100 и т.д. В основе древнеегипетской иероглифической системы лежали иероглифы. Другие числовые значения были получены в результате сложения основных чисел.
Римская система счисления — старая и декоративная
Наиболее известной сегодня является римская система счисления. Это зародилось в Древнем Риме, где вместо цифр использовались латинские буквы:
Латинская система счисления используется сегодня в декоративных целях: Он используется для цифр на часах, названий фильмов и глав книг:


В латинской системе счисления все числа получаются из хитроумных комбинаций различных буквенно-цифровых цифр, и все они зависят от того, какие цифры находятся рядом друг с другом.
В настоящее время общее правило выглядит следующим образом:
- цифры могут повторяться, но не более трёх одинаковых подряд;
- если меньшая цифра стоит справа от такой же или большей, то они складываются друг с другом: VIII → 8;
- если меньшая цифра стоит слева от большей — вычитаем из большего меньшее: IV → 4.
В древние времена, когда появилась римская система, не было вычитания — все прибавлялось, поэтому 4 записывалось не как IV, а как IIIIII. В древние времена все изменилось, и система превратилась в то, чем она является сегодня. По этой причине были добавлены шесть новых комбинаций, которые используются в расчетах в целом:
Перевод десятичного числа в римское
В качестве примера мы покажем вам, как перевести число 1998 в римскую систему счисления. Для этого выполните следующие действия:
- Берём самое большое римское число и смотрим, наше число больше или нет.
- Если наше больше — вычитаем из нашего римское и записываем его.
- Если не больше — переходим к следующему римскому.
- Так делаем до тех пор, пока у нас в остатке не получится ноль.
Вот как мы делаем это шаг за шагом:
- 1998 и 1000 (M) — самое большое римское число. Наше больше, поэтому отнимаем и добавляем новую букву: M. Остаток — 998
- Снова проверяем с самым большим числом — 1000 (M). Наше число меньше, поэтому берём следующее: CM (900). Это уже подходит, поэтому вычитаем его из 998: 998 − 900 = 98. Запоминаем остаток и добавляем CM к нашему числу: MCM
- Берём остаток — 98 — и проверяем снова все римские числа сверху вниз. Первое римское число, которое меньше нашего, — это XC (90). Отнимаем, получаем остаток 8 и добавляем XC к нашему числу: MCMXC
- Берём остаток — 8 — и смотрим, какое минимальное римское число меньше него, это V (5). Отнимаем пятёрку, получаем 3 и добавляем V к римскому числу: VCVXCV.
- Из числа 3 последовательно отнимаем три единицы I (1), и дописываем их к римскому числу: MCMXCVIII.
- У нас в остатке 0, а значит, мы закончили с переводом. 1998 = MCMXCVIII.
Зачем сейчас это знать
Системы неположительных чисел — это не только красивые записи чисел в эстетических целях, но и алгоритмы их вычисления. И если у вас есть алгоритм, вы можете написать для него код и использовать его в различных проектах.
В математике сегодня используются две системы неположительных чисел: биномиальная система чисел и система порядка остатков. Обе системы основаны на алгоритмах вычислений, и если вы понимаете разницу между ними и системами счисления, вам будет гораздо легче с ними работать.
Биномиальная система счисления существует, когда число представляется в виде суммы биномиальных коэффициентов. Слово «биномиальная» означает, что система основана на биномиальной системе Ньютона — методе, с помощью которого одни числа могут быть разложены на другие.
Эта система чисел используется в комбинаторике — с ее помощью можно быстро вычислить нужную комбинацию, не перебирая все предыдущие варианты. Это также используется для тестирования программного обеспечения, контроля качества и анализа лотерей — выявляются комбинации и сочетания факторов, которые, скорее всего, могли привести к каким-то значительным результатам.
Система категорий остатка основана на модульной арифметике, где числа сравниваются по модулю (если они дают одинаковый остаток при делении). Там все состоит из баз, модулей и похоже на работу с таблицами. Из-за свойства, что некоторые вычисления имеют только одно решение, система классов остатков используется в информационной безопасности, проверке ошибок и обеспечении надежности космической или военной техники.
Римская система счисления
В латинской системе основные числа записываются латинскими буквами I, V, X, L, C, D, M, а все остальные числовые значения получаются путем комбинирования этих букв по принципу сложения и вычитания.
Римская система названа по месту ее возникновения. Его использовали уже в Древнем Риме, две тысячи лет назад. Особенностью римской системы является то, что в ней не используется ноль.
Числа в латинской системе должны записываться слева направо, от самого большого к самому маленькому. Если перед числом стоит меньшая цифра, ее нужно вычесть из следующей цифры в соответствии с принципом вычитания. Младшие цифры, которые следуют за старшими, должны быть добавлены соответствующим образом.
Например, арабская цифра 1978 будет записана в латинской системе как MCMLXXVIII.
Римская система используется и сегодня для записи данных, указывающих на валентность химических элементов.
Древние непозиционные системы счисления
Историки знакомы с древними системами обозначений, которые используют различные знаки, символы и формы для представления числовых значений. Наиболее известными являются:
- Древнеегипетская система счисления
- Вавилонская система счисления
- Система счисления майя
Древнеегипетская система счисления
В древнеегипетской системе счисления специальные символы заменяли числа 1, 10, 100, 100, 1000, 1000 и так далее, кратные десяти.
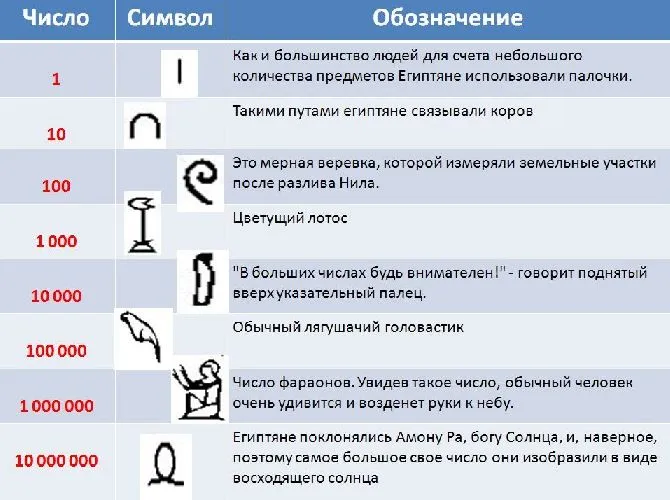
Числа записывались в виде комбинации таких символов, которые повторялись максимум девять раз в зависимости от значения конкретной цифры. Например, для числа 45 символ 10 был повторен четыре раза, а символ 1 — пять раз.
Вавилонская система счисления
Вавилонская система счисления использует символы в виде вертикальных и горизонтальных насечек — клиньев — для представления чисел. Эта система письма называется клинописью.
В древнем Вавилоне прямые клинья использовались для единиц, а горизонтальные — для десятков. Число шестьдесят также писалось прямым клином.
Вавилонская система счисления также называется шестнадцатеричной системой. Принцип деления диапазона чисел на группы по 60 используется и сегодня для определения временных интервалов. Час состоит из 60 минут, минута — из 60 секунд.
Вавилонская система представляет собой комбинированный вариант системы счисления, поскольку представление чисел от 1 до 60 подчиняется непозитивному принципу, в то время как числа выше шестидесяти представляются с позитивным приближением.
Например, число 34 в вавилонской системе записывается как серия из трех горизонтальных клиньев, за которыми следуют четыре прямых клина. А число 84 будет начинаться с прямого клина, представляющего 60, за которым следуют два горизонтальных клина, а затем четыре прямых клина.
Система счисления майя
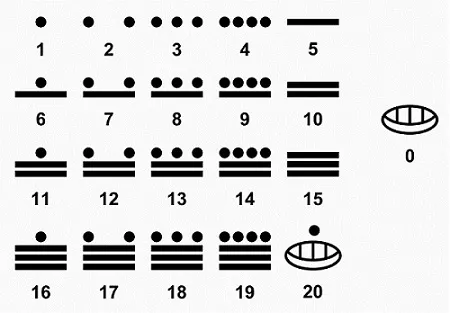
Для обозначения чисел в различных бытовых ситуациях майя использовали систему представления чисел без цифр, в которой числа от 0 до 19 записывались символами, состоящими из комбинаций точек и горизонтально расположенных сегментов.
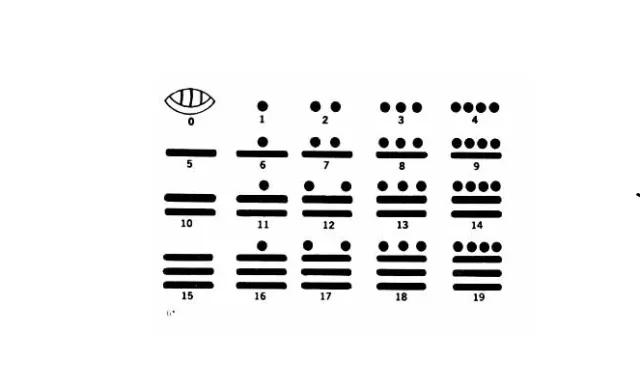
Например, цифра для числа 17 выглядит как две точки над тремя горизонтальными штрихами.