Существует один путь через B и три пути через C к вершине D, поэтому общее количество путей равно 4. Аналогично, существует 4 пути к вершине E: 3 пути через B и один через G (рисунок 3.35).
Графы: разные виды представления графов. Алгоритмы Дейкстры и Флойда: реализация на Python. Минимальное остовное дерево
Метод обхода графов, при котором сначала выполняется обход от последней посещенной вершины (вершины хранятся в стеке). Обход в глубину, конечно, достигается путем рекурсивного обхода графа.
# Смежность вершин inc =<1: 2, 8, 2: 1, 3, 3: 4, 4: 7, 9, 5: 6, 6: 5, 7: 8: 9:>visited = set() # Посещена ли вершина? # Поиск в глубину (DFS) def dfs(v): if v in visited: # Если вершина уже посещена, возвращается visited.add(v) # Посещенная вершина v for i in incv: # Все вершины, смежные с v if not i in visited: dfs(i) start = 1 dfs(start) # start - начальная вершина обхода print(visited)
Поиск в ширину — ПВШ (Breadth First Search — BFS)
Обход графа, при котором мы сначала делаем переход от первого еще не посещенного узла (узлы хранятся в очереди). Обход по глубине, конечно, достигается рекурсивным обходом графа.
Порядок точек, которые необходимо обойти, следующий
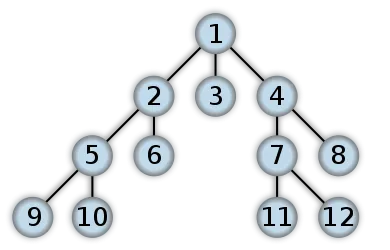
# Смежность вершин inc =<1: 2, 8, 2: 1, 3, 3: 4, 4: 7, 9, 5: 6, 6: 5, 7: 8: 9:>visited = set() # Если вершина посещена; Q = # BFS queue = # Breadth First Search (BFS) def bfs(v): if v in visited: # Если вершина уже посещена, exit return visited.add(v) # Посещенная вершина v BFS. append(v) # Запомните порядок прохождения # print("v = %d" % v) for i in incv: # Все вершины, смежные с v if not i in visited: Q. append(i) while Q: bfs(Q.pop(0)) start = 1 bfs(start) # start - первая вершина прохождения print(BFS) # Выход: 1, 2, 8, 3, 7, 4, 5, 9, 6
Поиск кратчайших путей в графах (объединение разделов по Дейкстре и Флойду)
Алгоритм Дейкстры — это алгоритм для графов, который находит кратчайшее расстояние от одной из вершин графа до всех остальных вершин. Алгоритм работает только для графов без ребер с отрицательным весом (без ребер с отрицательной «длиной»).
Примеры проблемы
Вариант 1. Существует сеть дорог, соединяющих города. Некоторые дороги являются дорогами с односторонним движением. Найти кратчайшие дороги из данного города в любой другой город (если дороги являются единственным способом передвижения).
Вариант 2: Существует несколько рейсов между городами мира, для каждого из которых известна стоимость. Стоимость перелета из А в Б может отличаться от стоимости перелета из Б в А. Найдите самый дешевый маршрут (возможно, с пересадкой) из Копенгагена в Барнаул.
Идея алгоритма Дейкстры
Алгоритм состоит из 2 итерационных шагов:
- Добавление новой вершины («Расти» — GROW )
- «Релаксация», т.е. пересчёт расстояний до других вершин с учётом добавленной вершины ( RELAX ).
Более подробное описание:
Примечания:
Граф $G = (V,E)$, где $V$ — вершины, а $E$ — ребра.
$v_0$ — начальная вершина (от которой мы ищем кратчайшее расстояние до всех остальных).
$R_i$ — известное расстояние от вершины $v_0$ до вершины $i$.
$D$ — это множество вершин, от которых известно кратчайшее расстояние до $v_0$.
Граф $G=(V,E)$, где $V$ — вершины, а $E$ — ребра.
$v_0$ — начальная точка вершины
$R_i$ — кратчайшее расстояние от $v_0$ до $i$-й вершины.
Инициализация алгоритма:
$D = \$ — пустое множество.
$R_ = 0$ — расстояние от $v_0$ до $v_0$ = 0$.
$v = v_0$ — мы будем расти из вершины $v$.
Итерация (общий шаг алгоритма).
$GROW(V/D,v)$ — Добавляет вершину $v$ из множества $V/D$ в множество $D$.
$RELAX(V/D,v)$ — обходит достижимые вершины $v$, до которых мы еще не знаем кратчайшего расстояния, и обновляет расстояние $R_i$ от вершины $v$.
$v$ — вершина с минимальным $R$ из множества $V/D$.
Пока нам удается расти (операция $GROW$ добавляет вершину).
Алгоритм
Каждой вершине $v$ из $V$ присваивается значение $av$, то есть минимальное известное расстояние этой вершины от начальной точки $s$. Алгоритм работает пошагово — на каждом шаге рассматривается вершина и делается попытка улучшить текущее расстояние до этой вершины. Алгоритм завершается, когда все вершины посещены или когда вычислены расстояния до всех вершин, достижимых из начальной точки.
Инициализация. Значение $as$ самого начального узла принимается равным 0, значение остальных узлов — бесконечным (в программировании это делается путем присвоения большого, например, максимально возможного значения для данного типа). Это отражает тот факт, что расстояния от $s$ до других вершин еще не известны.
Шаг алгоритма: Когда все вершины посещены, алгоритм завершается. В противном случае, вершина v, имеющая наименьшее расстояние до исходной вершины $s$, выбирается из непосещенных вершин и добавляется в список посещенных вершин. Эта вершина находится с помощью перечисления всех непосещенных вершин. Она суммирует расстояние от начала координат до одной из посещенных вершин u и до непосещенных вершин $v$. На первом этапе $s$ является единственной посещенной вершиной, расстояние которой от начала координат (т.е. от самой себя) равно 0.
Введение
Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах и предназначен для поиска кратчайших путей между заданной вершиной и всеми другими вершинами графа.
В общем случае графом называется набор вершин и ребер, где число ребер может быть задано числом, а число вершин — числом
Для каждого ребра в графе задается неотрицательный вес by, а также узел, из которого осуществляется поиск оптимальных путей.
Алгоритм Дейкстры может найти кратчайший путь между узлами и в графе только в том случае, если между этими узлами существует хотя бы один путь. Если это условие не выполняется, алгоритм работает корректно и возвращает значение «бесконечность» для пары несвязанных вершин.
Условие неотрицательности весов ребер является чрезвычайно важным и не может быть проигнорировано. Невозможно свести задачу к решению с помощью алгоритма Дейкстры, добавив ко всем ребрам наибольший вес по модулю. Это может изменить оптимальный путь. На рисунке видно, что в первом случае оптимальный путь между и (сумма ребер в пути наименьшая) изменяется в результате этой манипуляции. В исходном варианте путь проходит через, а после добавления семи ко всем ребрам, оптимальный путь проходит через
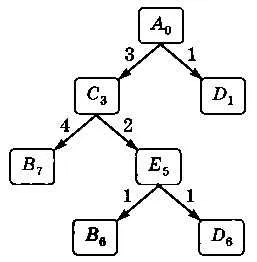
Как ведет себя алгоритм Дейкстры на исходном графе, будет решено, когда мы напишем алгоритм. Но давайте сначала зададим другой вопрос: «Почему бы не применить амплитудный поиск к нашему графу?». Хорошо известно, что метод BFS находит оптимальный путь от каждой вершины ориентированного графа к каждой другой вершине, но это справедливо только для ребер с единичным весом.
Можно свести задачу к разрешимой BFS, но если заменить все ребра без единичного веса на ребра с единичным весом, граф становится слишком большим, что приводит к большому количеству операций при вычислении оптимального пути.
Чтобы избежать этого, мы предлагаем использовать алгоритм Дейкстры. Давайте опишем его:
- Задаём множество, состоящее из исходной вершины.
- Массив длин кратчайших путей, в котором изначально есть, кратчайших путь от вершины до себя самой.
Основной цикл алгоритма:
- Пока все вершины не исследованы (или формально ), повторяем:
- Среди всех рёбер в графе таких, что, а, выбираем одно, которое минимизирует сумму:
- Добавяем эту вершину в .
- Задаём равным
В результате выполнения этого алгоритма таблица содержит все оптимальные пути, начиная с .
Примеры работы
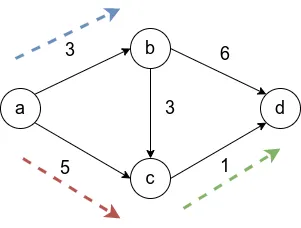
Подумайте над приведенной выше схемой и поищите пути к чему-либо на этой схеме.
На первом шаге алгоритма определяется, что кратчайший путь ведет в направлении синей стрелки, и определяется кратчайший путь. На втором этапе рассматриваются все возможные варианты, и оказывается, что оптимальным вариантом является движение по красной стрелке, так как меньше и прибавляется длина кратчайшего пути. Наконец, на третьем этапе, когда уже есть три вершины в, нужно рассмотреть только два ребра, и выбирается вариант вдоль зеленой стрелки.
Давайте теперь рассмотрим приведенную выше диаграмму с отрицательными весами. Хочу напомнить, что алгоритм Дейкстры может работать некорректно на таком графе.
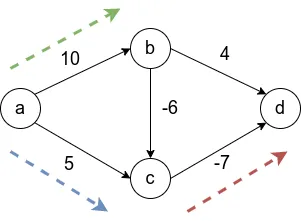
Первым шагом является выбор ребра вдоль синей стрелки, так как это ребро с наименьшим весом исходной вершины. Затем выбирается край. Это навсегда фиксирует ложный путь от до, в то время как оптимальный путь с отрицательным весом проходит через центр. На последнем этапе добавляется вершина to.
Оценка сложности алгоритма
До этого момента мы разъясняли сам алгоритм, ограничения, которые он накладывает, и некоторые примеры его реализации. Здесь следует упомянуть о сложности этого алгоритма, поскольку он полезен для решения задач, для которых была разработана эта статья. В базовом подходе на основе циклов обходятся все ребра каждого узла, что приводит к сложности.
Эффективная реализация предполагает использование кучи. Короткий ответ на эту структуру данных заключается в том, что она позволяет выполнять две операции за логарифмическое время. Первая операция — найти узел в дереве с наименьшим ключом, а вторая — вставить в дерево новый узел с новым ключом.
Что еще можно сказать об этой куче:
- это сбалансированное бинарное дерево,
- ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.
В этой заметке я уже рассказывал об интересной проблеме с кучами.
Используя в алгоритме Дейкстры кучу, где в качестве ключей выступают расстояния от узла в непокрытой части графа (в алгоритме это ) до ближайшего узла в уже покрытой части (это множество узлов ), мы можем уменьшить вычислительную сложность Доказательство ценности этих оценок я оставляю за рамками этой статьи.
Теперь перейдем к проблемам анализа!
Учитель информатики
Обработка данных. Учебник для 9 класса (по книге К.Я. Полякова, Е.А. Еремина, базовый уровень).
§17. Графы.
Что такое граф?
Ключевые слова:
- Граф - узлы - ребра - матрица смежности - степень узла - связный граф - взвешенный граф - взвешенная матрица - ориентированный граф - оптимальный путь - число путей.
Давайте рассмотрим, как можно визуализировать эту информацию:
Из Васюков в Солнцево ведут три дороги: Грибное и Ягодное. Также есть дороги между Солнцевом и Грибным и между Грибным и Ягодным. Есть также дорога из Грибного в лес и обратно в Грибное. Нарисуйте в своем блокноте дорожную карту на основе этого описания.
Например, можно нарисовать следующую диаграмму (рисунок 3.17, а).
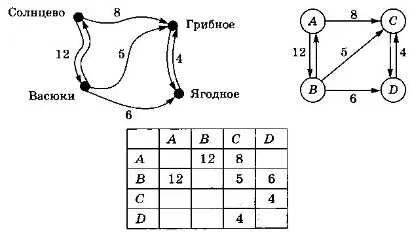
Рисунок 3.17
В информатике для изучения таких диаграмм используются графы.
Граф состоит из набора узлов (вершин) и связей между ними (ребер).
Схема, соответствующая нашей дорожной системе, показана на рис. 3.17, b, для простоты населенные пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и соединениях на приведенной выше диаграмме можно использовать таблицу, подобную этой (рис. 3.18).
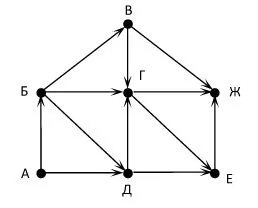
Рисунок 3.18
Единица на пересечении строки A и столбца B указывает на наличие связи между узлами A и B. Ноль означает отсутствие связи. Такая матрица называется матрицей смежности. Он симметричен относительно главной диагонали (см. заштрихованные клетки в таблице).
Рассмотрите матрицу смежности и сравните ее с диаграммой на рис. 3.17, б. Что означает пересечение столбца C и строки C?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степень вершины — это количество ребер, с которыми вершина соединена. Петля учитывается дважды (оба конца ребра соединены с вершиной!).
Используйте таблицу смежности, чтобы вычислить, сколько ребер имеет граф. Определите степени всех вершин. Как вы это обосновали?
Строго говоря, график — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (как на рисунке 3.17b), но матрица смежности не скажет вам, как именно вершины соотносятся друг с другом. Для приведенной выше матрицы, например, возможны такие вариации (рис. 3.19).

Рис. 3.19
Нарисуйте два разных изображения графа, используя матрицу смежности (рис. 3.20).
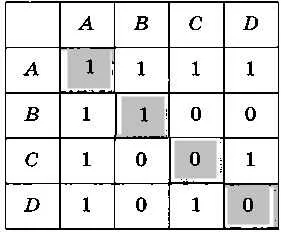
Рисунок 3.20.
Граф имеет 4 вершины, и каждая вершина соединена ребрами со всеми остальными вершинами. Нарисуйте эту диаграмму. Сколько ребер в графе?
Граф имеет N вершин, и каждая вершина соединена со всеми другими вершинами. Сколько ребер в графе?
Граф имеет 4 ребра. Какова сумма степеней вершин графа? Зависит ли это от количества вершин?
Взвешенный граф
В нашем примере, если нас интересуют не только дороги между населенными пунктами, но и расстояние между ними, мы должны добавить вес ребра к каждому соединению (рисунок 3.22).
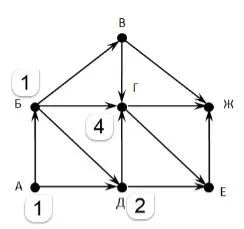
Рисунок 3.22
Взвешенный граф — это граф, в котором каждое ребро связано с определенным числом — весом ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или какая-то другая величина.
Как мы можем хранить информацию на таком графе? Ответ очевиден: в таблице мы пишем не 1 или 0, а вес ребра. Если между двумя узлами нет связи, мы можем оставить ячейку таблицы пустой на бумаге, а если она хранится в памяти компьютера, мы можем записать на ней условный код, например, числ о-1 или очень большое число. Такая таблица называется таблицей весов, поскольку она содержит веса ребер. В этом случае она имеет следующий вид (рис. 3.23).
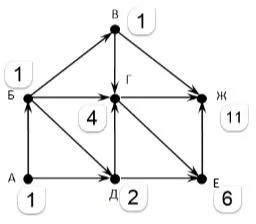
Рисунок 3.23
Как и матрица смежности, матрица веса симметрична относительно диагонали.
Что означают пустые ячейки в таблице веса?
Как вы можете использовать таблицу весов, чтобы сразу определить, сколько ребер у графа?
Используя таблицу весов (рисунок 3.24), определите длины путей ADBEC, ABDCE, DEBAC. Как вы это обосновали?
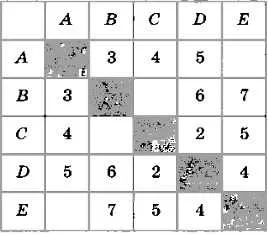
Рисунок 3.24.
Оптимальный путь в графе
Чтобы определить оптимальный (лучший) путь между двумя узлами графа, необходимо ввести числовой индекс для сравнения путей с целью определения лучшего. Обычно для оценки пути используется сумма весов ребер, составляющих путь. Например, при поиске кратчайшего маршрута, чем меньше значение, тем лучше.
Какие мерила вы используете в своей жизни, чтобы найти лучший путь? Всегда ли кратчайший путь является наилучшим?
Если граф имеет всего несколько узлов, матрица весов может быть использована для поиска наилучшего пути от одного узла к другому с помощью простой атаки методом перебора. Рассмотрим граф, заданный матрицей весов на рис. 3,25 (цифры указывают на стоимость перемещения между соседними точками).
Рис. 3.25
Мы хотим найти наилучший путь из A в B — путь, который минимизирует общую стоимость поездки.
Чтобы решить эту проблему, создадим дерево перечислений. Мы видим, что из точки А непосредственно
Рис. 3.26.
Числа возле ребер обозначают стоимость проезда по данному участку, а индексы в узлах обозначают общую стоимость проезда до этого узла из A. Теперь рассмотрим вариации дальнейшего удаления от узла C I tM lt;pb p (рис. 3.27).
Рисунок 3.27
Как вы думаете, почему на диаграмме не показана возможность перехода из C в A?
Мы видим, что из C в B можно доехать напрямую, поэтому стоимость проезда равна 7.
Обход в ширину
F: Кратчайший путь в 0-1-графе
Существует городская транспортная система (неориентированная диаграмма), включающая автобусы и троллейбусы. Автобус стоит 1 доллар, а билет на трамвай бесплатный. Найдите самый дешевый способ добраться от одной остановки до другой. Если такого способа нет, выводитс я-1.
Сложность полученного алгоритма должна быть \(O(|V| + |E|)\).
6 6 1 2 1 2 3 0 3 4 1 1 6 0 6 5 1 5 4 0 3 1 4 2 3 2 6
G: Кратчайший цикл
Дается ориентированный граф. Необходимо извлечь один из самых коротких кругов. Если кругов нет, выводитс я-1.
Сложность полученного алгоритма должна быть \(O(|V|\cdot(|V| + |E|))\).
H: Кратчайший чётный путь
Дан ориентированный граф и несколько пар его вершин. Выделите кратчайший путь четной длины из одной вершины в другую ил и-1, если такого пути не существует.
Сложность полученного алгоритма должна быть \(O(|V| + |E|)\).
Эйлеров путь
I: Поиск эйлерова пути
В городе есть $N$ квадратов, соединенных дорогами. Количество улиц не превышает $100000$ и есть не более трех кварталов с нечетным количеством улиц. Для каждой дороги известна ее длина. Движение разрешено на каждой улице в обоих направлениях. В городе есть как минимум одна улица. По улицам можно пройти от любой площади до любой другой площади. Почтальон должен зайти на каждую улицу хотя бы один раз. Почтальон хочет, чтобы его прогулка была как можно короче. Она может начинаться на любой клетке и заканчиваться на любой клетке (включая начальную). Помогите почтальону составить такой маршрут. Сначала напишите число $N$ — количество квадратов в городе $(2\leqslant N\leqslant1000)$. Затем пройдите по $N$ линиям, определяющим улицы. На $i$-й из этих линий находится число $m_i$ — количество улиц, выходящих из $i$-квадрата. Далее следуют $m_i$ пар натуральных чисел: в $j$-й паре первое число — номер квадрата, в который ведет $j$-я дорога из $i$-го квадрата, а второе число — длина этой дороги. Между двумя квадратами может быть более одной дороги, но не может быть дороги от квадрата к самому квадрату. Все числа во входном файле не должны превышать $100000$. Если решение есть, поставьте в первой строке выходного файла число — количество дорог на искомом маршруте — и номера квадратов в порядке их посещения во второй строке. Если решения нет, то в выходной файл записывается число $-1$. Если существует несколько решений, укажите одно из них.
Компоненты сильной связности, метаграфы и мосты; компоненты двусвязности и точки сочленения
J: Компоненты сильной связности
Существует ориентированный граф. Подмножество его вершин называется элементом сильной связности, если между любыми двумя вершинами графа существует путь и при этом нельзя добавить больше вершин без потери этого свойства.
Извлеките количество компонентов с сильной связностью, затем список вершин каждого компонента, разделенных пробелом. Отсортируйте вершины каждой компоненты в лексикографическом порядке, а сами компоненты — в порядке возрастания «наименьшей» вершины.
Сложность полученного алгоритма должна быть \(O(|V| + |E|)\).
10 14 4 9 7 8 2 5 1 4 9 2 10 6 6 5 8 3 5 9 4 3 8 7 5 1 2 1 6 10
K: Конденсация графа (метаграф)
Дан ориентированный граф с $N$ вершинами и $M$ ребрами $(1\leqslant N\leqslant20000, 1\leqslant M\leqslant200000)$. Теперь перетащите каждый компонент сильной связности в отдельную вершину (мета-вершину) и оставьте только ребра между мета-вершинами, удалив дубликаты. Полученный граф называется метаграфом (мета-графом) исходного графа или его компактификацией. Постграф любого ориентированного графа является ациклическим и может быть топологически упорядоченным.
Найти компоненты сильной связности заданного графа и топологически классифицировать его компактификацию. График определяется во входном файле следующим образом: Первая строка содержит числа $N$ и $M$. Каждая из следующих строк $M$ содержит описание ребра — два целых числа в диапазоне от $400$ до $N$ — номера начала и конца ребра. В первой строке выводится $K$ — количество компонент сильной связности в данном графе. Следующая строка выводит $N$ — для каждой вершины номер компоненты сильной связности, к которой принадлежит эта вершина. Компоненты сильной связности должны быть пронумерованы таким образом, чтобы для каждой вершины номер начального компонента сильной связности не превышал номер конечного компонента сильной связности.
10 14 4 9 7 8 2 5 1 4 9 2 10 6 6 5 8 3 5 9 4 3 8 7 5 1 2 1 6 10
L: Поиск мостов
Дан неориентированный граф. Ребро называется мостом или перешейком, если число компонентов связности увеличивается в зависимости от расстояния до него. Соответствующее определение гласит, что ребро является мостом только в том случае, если оно не содержится в цикле.
Извлечение списка мостов графа, отсортированных в лексикографическом порядке (вершины каждого ребра также должны быть отсортированы).
Сложность полученного алгоритма должна быть \(O(|V| + |E|)\).
M: Поиск точек сочленения
Дан неориентированный граф. Вершина называется шарнирной или точкой шарнира, если после ее вычитания количество соединяющих элементов увеличивается.
Извлечение списка связных точек, отсортированных в лексикографическом порядке.
Сложность полученного алгоритма должна быть \(O(|V| + |E|)\).
Поиск в ширину (BFS, Breadth-First Search)
Алгоритм был разработан независимо Муром и Ли в 1959 и 1961 годах для различных приложений (ориентирование в лабиринте и картирование трубопроводов, соответственно). Этот алгоритм можно сравнить с освещением соседних узлов графа: Сначала зажигается один узел (тот, с которого начинается путь), а затем огонь распространяется на все соседние, неосвещенные узлы за элементарный промежуток времени. Затем то же самое происходит со всеми освещенными вершинами. Таким образом, огонь распространяется «далеко». В результате будет найден кратчайший путь к нужной ячейке.
Этот алгоритм назван в честь своего изобретателя и был разработан в 1959 году. В процессе работы алгоритм рассматривает каждый узел графа и находит кратчайший путь к исходному узлу. Типичная реализация работает с взвешенным графом — графом, в котором каждый путь имеет вес, то есть «стоимость», которую нужно «заплатить», чтобы пройти через эту вершину. В типичной реализации весовые коэффициенты неотрицательны. В клетчатой коробке вес каждого ребра графа предполагается равным (например, единице).
А* (А «со звездочкой»)
Впервые он был описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Этот алгоритм является расширением алгоритма Дейкстры, ускорение достигается за счет эвристики — по мере рассмотрения каждого узла осуществляется переход к соседнему узлу, который, как предполагается, является кратчайшим путем к искомому узлу. Существует множество различных методов расчета длины предполагаемого пути от вершины. Результат также является кратчайшим путем. Подробнее о реализации алгоритма читайте здесь.
Улучшенная версия алгоритма поиска по ширине, отличающаяся от оригинального алгоритма тем, что сначала используются узлы, от которых путь к конечному узлу считается кратчайшим. Это означает, что он делает для BFS то, что A* делает для алгоритма Дейкстры за счет эвристики.
IDA* (A* с итеративным углублением)
Он определяется как повторение скважины A*. Это модифицированная версия A*, которая требует меньше памяти, поскольку отбрасывается меньшее количество узлов. Он быстрее, чем A*, если эвристика подобрана правильно. В результате получается кратчайший путь.
Последний из перечисленных алгоритмов был представлен в 2011 году и является улучшенным по сравнению с A*. JPS ускоряет поиск маршрута, «пропуская» несколько мест, которые необходимо рассмотреть. В отличие от аналогичных алгоритмов, JPS не требует предварительной обработки и дополнительных затрат памяти.
Мы рассмотрели материал о более интересных алгоритмах в коллекции Advanced Algorithms and Data Structures.
Задача о кратчайшем пути между всеми парами вершин править | править код
Проблема кратчайшего пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена в 1953 году Симбелом15, который обнаружил, что она может быть решена линейным числом матричных манипуляций (умножений). Сложность такого алгоритма составляет O ( V 4 ).
Существуют и другие более быстрые алгоритмы для решения этой задачи, такие как алгоритм Флойда-Уоршелла со сложностью O ( V 3 ) и алгоритм Джонсона (комбинация алгоритмов Беллмана-Форда и Дейкстры) со сложностью O ( VE + V 2 log V ).
Применение править | править код
Проблема поиска кратчайшего пути в графе может быть интерпретирована по-разному и применена к различным областям. Ниже приведены примеры различных применений этой проблемы. Другие приложения изучаются в области исследования операций.
Картографические сервисы править | править код
Алгоритмы поиска кратчайшего пути в графе используются для поиска путей между физическими объектами в картографических сервисах, таких как Google Maps или OpenStreetMap. В обучающем видео Google можно узнать о нескольких эффективных алгоритмах, применяемых в этой области17 .
Недетерминированная машина править | править код
Если рассматривать недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра — возможные переходы, то алгоритмы поиска кратчайшего пути могут быть применены для нахождения оптимальной последовательности решений для достижения главной цели. Например, если вершины — это состояния кубика Рубика, а ребро представляет собой одно действие в кубике, то алгоритм может быть применен для поиска решения с наименьшим количеством ходов.
Сети дорог править | править код
Проблема поиска кратчайшего пути в графе часто используется для определения кратчайшего маршрута в дорожной сети.
Дорожная сеть может быть представлена в виде графа с положительными весами. Вершины — это узлы дорог, а ребра — дороги, которые их соединяют. Вес ребра может соответствовать длине конкретного участка, времени, затраченному на его прохождение, или стоимости его прохождения. Ориентированные ребра могут быть использованы для представления улиц с односторонним движением. В такую диаграмму можно вставить функцию, указывающую на то, что некоторые дороги более важны для дальних перевозок, чем другие (например, автомагистрали). Она была формализована в концепции (идее) автомобильных дорог18 .
Существует множество алгоритмов реализации этой концепции, причем некоторые дороги важнее других. Они решают проблему поиска кратчайшего пути гораздо быстрее, чем обычные графы. Эти алгоритмы состоят из двух этапов:
- этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
- этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.
Самый быстрый алгоритм может решить эту задачу на европейских или американских дорогах за доли микросекунды 19 .
Другие подходы (методы), которые были использованы в этой области:
Похожие задачи править | править код
Существуют задачи, аналогичные задаче поиска кратчайшего пути в графе.
- Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
- Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
- Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
- Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина 20 .