Как создать собственную нейронную сеть с нуля на языке Python. Искусственный интеллект на python.

Мнестические данные содержат оцифрованные изображения рукописных цифр и поэтому имеют значения от 0 до 255. Чтобы нормализовать данные, разделите входные данные на 255 так, чтобы распределение изображений было между 0 и 1.

Python AI: как построить нейронную сеть и делать прогнозы

Проще говоря, цель использования искусственного интеллекта заключается в том, чтобы заставить компьютеры думать как люди. Это может показаться чем-то новым, но данная область зародилась в 1950-х годах.

Представьте, что вам нужно написать программу на языке Python, которая использует искусственный интеллект для решения задачи судоку. Для этого вы пишете условные команды и проверяете ограничения, чтобы узнать, можно ли поместить число в каждую позицию. Теперь этот сценарий Python уже является приложением ИИ, потому что вы запрограммировали компьютер на решение проблемы!

Машинное обучение (ML) и глубокое обучение (DL) также являются подходами к решению проблем. Разница между этими методами и скриптами Python заключается в том, что ML и DL используют обучающие данные, а не жестко заданные правила, но все они могут быть использованы для решения проблем с помощью ИИ. В следующих разделах вы узнаете больше о том, что отличает эти два метода.

Машинное обучение

Машинное обучение — это метод обучения системы решению проблемы, а не явное программирование правил. Чтобы решить проблему с помощью машинного обучения, необходимо собрать данные из решенных игр судоку и обучить статистическую модель.Статистические модели— это математически стандартизированные методы для аппроксимации поведения явления.

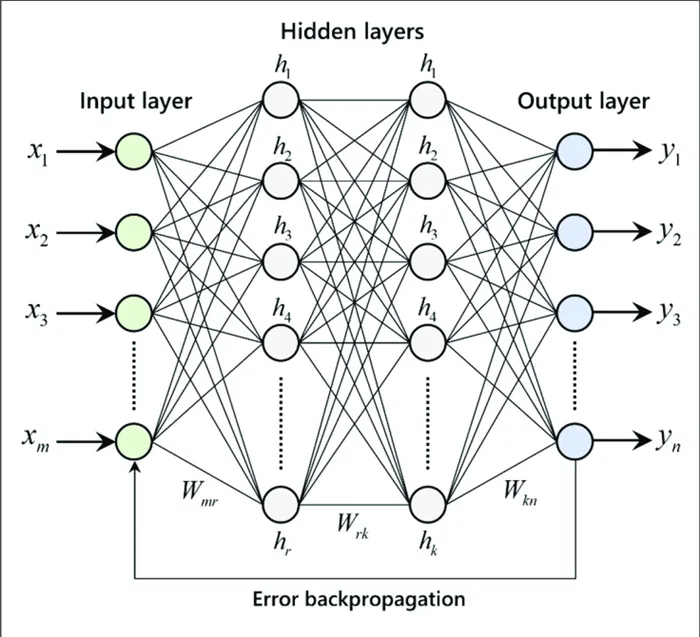
Распространенной задачей в машинном обучении является обучение с помощью учителя, когда имеется набор данных с входными данными и известными выходными данными. Цель состоит в том, чтобы использовать этот набор данных для обучения модели, которая предсказывает правильный выход на основе входных данных. На следующем рисунке показан рабочий процесс обучения модели с помощью преподавателя:

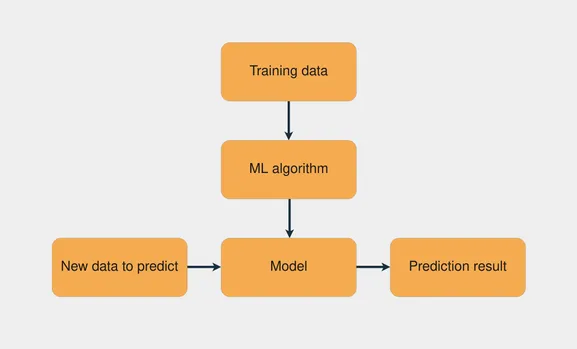
Комбинируя обучающие данные с алгоритмом машинного обучения, создается модель. Алгоритм обучения использует алгоритм машинного обучения для создания модели.

Примечания. Scikit-learn — это популярная библиотека машинного обучения на языке Python, которая предлагает множество алгоритмов обучения с помощью учителя и без него. Чтобы узнать больше, смотрите раздел Разделение набора данных с помощью функции train_test_split() от scikit-learn.

Цель задач контролируемого обучения заключается в том, чтобы делать прогнозы относительно новых, невидимых данных. Предполагается, что эти невидимые данные имеют такое же распределение вероятности, как и обучающий набор данных. Если в будущем это распределение изменится, необходимо заново обучить модель на новом наборе обучающих данных.

Разработка функций

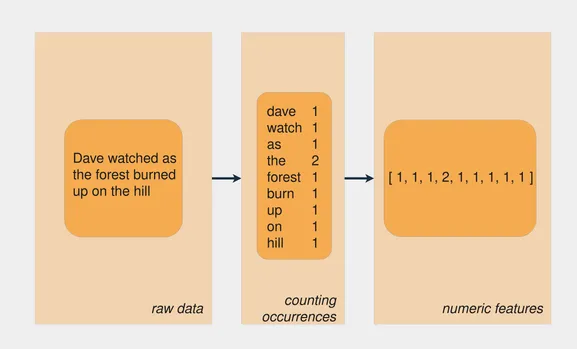
Проблемы прогнозирования усложняются, когда в качестве исходных данных используются различные типы данных. Задача судоку относительно проста, потому что вы имеете дело непосредственно с числами. Что если вы хотите научить модель предсказывать настроение в предложении? Или что если у вас есть фотография и вы хотите узнать, есть ли на ней кошка?

Другое название входных данных — функция, а проектирование функций — это процесс извлечения функций из исходных данных. Когда вы работаете с различными типами данных, вам необходимо найти способы представления этих данных, чтобы извлечь из них важную информацию.

Нейронные сети: основные понятия

Нейронная сеть — это система, которая учится делать прогнозы с помощью следующих шагов:

1. Получение входных данных
2. Делаем прогноз
3. Сравнение прогноза с желаемым результатом
4. Настройка его внутреннего состояния для правильного прогнозирования в следующий раз

Векторы, слои и линейная регрессия являются одними из строительных блоков нейронных сетей. Данные хранятся в виде векторов, а в Python вы храните эти векторы в таблицах. Каждый уровень преобразует данные предыдущего уровня. Каждый слой можно рассматривать как шаг в разработке функции, потому что каждый слой извлекает представление данных, которые предшествовали ему.

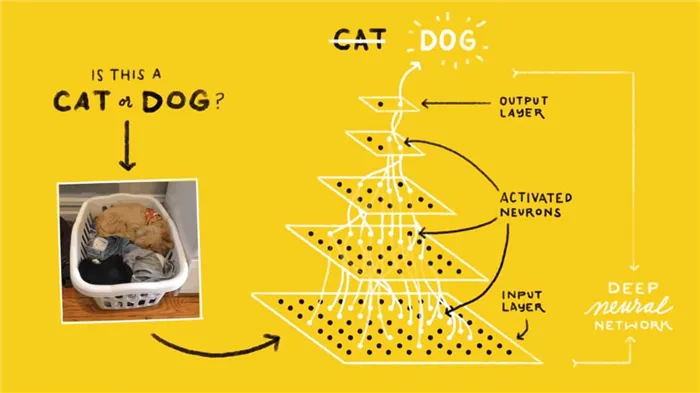
Слои нейронной сети интересны тем, что одно и то же вычисление может извлечь информацию из любых данных. Это означает, что не имеет значения, используете ли вы данные изображения или текстовые данные. Процесс извлечения значимой информации и обучения модели глубокого обучения одинаков для обоих сценариев.

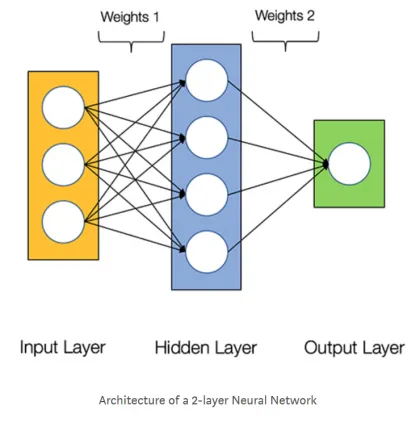
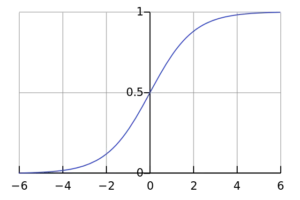
На следующем рисунке показан пример сетевой архитектуры с двумя уровнями:

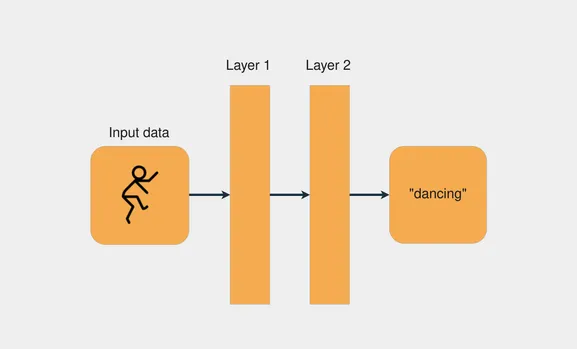
Каждый слой преобразует данные, полученные от предыдущего слоя, применяя определенные математические операции.

Процесс обучения нейронной сети

Обучение нейронной сети — это процесс проб и ошибок. Представьте, что вы впервые играете в дартс. При первом выстреле вы стараетесь попасть в центр мишени. Обычно первый выстрел делается только для того, чтобы посмотреть, как высота и скорость вашей руки влияют на результат. Если вы видите, что стрелка находится выше центральной точки, отрегулируйте руку, чтобы бросить ее немного ниже, и так далее.

Вот шаги, которые нужно предпринять, чтобы попасть в центр доски для игры в дартс:

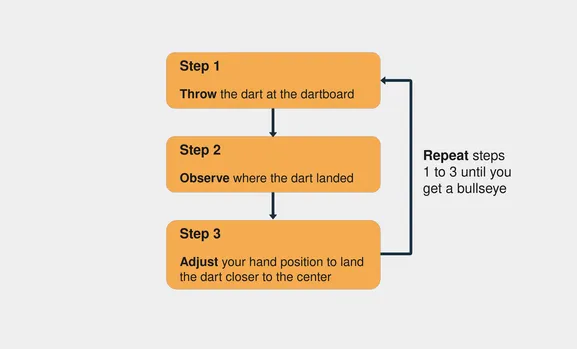
Обратите внимание, что вы продолжаете оценивать ошибку, наблюдая за местом приземления дротика (шаг 2). Продолжайте, пока не попадете в центр мишени.

В нейронных сетях процесс очень похож: вы начинаете со случайных весов и векторов смещения, делаете прогноз, сравниваете его с желаемым результатом и корректируете векторы для получения более точного прогноза в следующий раз. Процесс продолжается до тех пор, пока разница между предсказанием и правильными целями не станет минимальной.

Знание того, когда следует прекратить обучение и какую цель точности установить, является важным аспектом обучения нейронной сети, особенно в связи со сценариями пере- и недообучения.

Векторы и веса

Работа с нейронными сетями заключается в выполнении операций с векторами. Представьте векторы в виде многомерных матриц. Векторы полезны в Deep Learning прежде всего благодаря одной конкретной функции: скалярному произведению. Скалярное произведение двух векторов показывает, насколько они похожи по направлению, и изменяется в зависимости от размера двух векторов.

Наиболее важными векторами в нейронной сети являются векторы веса и смещения. В общем, нейронная сеть должна проверить, похожи ли входные данные на другие входные данные, которые она уже видела. Если новые входные данные похожи на ранее наблюдаемые входные данные, то выходные данные также будут похожи. Так вы получите результат предсказания.

Python AI: начинаем строить свою первую нейронную сеть

Первым шагом в построении нейронной сети является генерация выходных данных из входных. Это делается путем создания взвешенной суммы переменных. Первое, что необходимо сделать, это представить входные данные с помощью Python и NumPy.

Обертывание входных данных нейронной сети с помощью NumPy

Вы будете использовать NumPy для представления входных векторов сети в виде таблиц. Однако прежде чем использовать NumPy, следует поиграть с векторами в чистом Python, чтобы лучше понять, что происходит.

В этом первом примере у вас есть один входной вектор и два других весовых вектора. Цель состоит в том, чтобы найти веса, которые наиболее похожи на входные данные, принимая во внимание направление и величину. Вот как выглядят векторы, когда вы их рисуете:

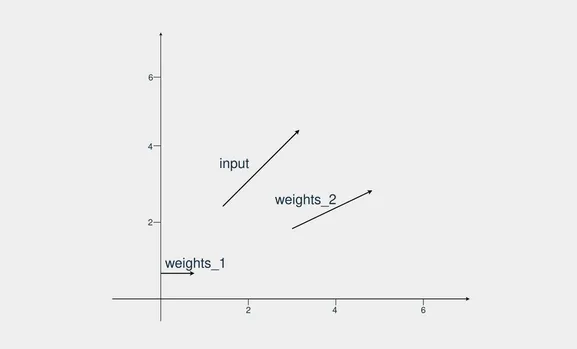
Вес_2 более похож на входной вектор, поскольку он направлен в ту же сторону, и значение также похоже. Как же с помощью Python определить, какие векторы похожи?

Сначала вы определяете три вектора, один для входа, а два других — для весов. Затем вы вычисляете, насколько похожи входной вектор и вес_1. Для этого применяется скалярное произведение. Поскольку все векторы являются двумерными векторами, необходимо выполнить следующие действия:

1. Умножьте первый индекс input_vector на первый индекс weights_1 .
2. Умножьте второй индекс input_vector на второй индекс weights_2 .
3. Суммируйте результаты обоих умножений.

Для выполнения инструкций можно использовать консоль IPython или блокнот Jupyter. Хорошей практикой является создание новой виртуальной среды каждый раз, когда вы начинаете новый проект Python. Venv поставляется с Python версии 3.3 и выше и полезен для создания виртуальных сред.

Эта статья будет продолжена позднее.

Что такое нейронная сеть?

Большинство статей о нейронных сетях при их описании начинают с мозга. Мне проще описать нейронные сети как математическую функцию, которая сопоставляет заданный вход с желаемым выходом, не вдаваясь в подробности.

Нейронные сети состоят из следующих элементов:

• входной слой, x
• произвольное количество скрытых слоев
• выходной слой, ŷ
• набор весов и смещений между каждым слоем W и b
• выбор функции активации для каждого скрытого слоя σ ; в этой работе мы будем использовать функцию активации Sigmoid

На схеме ниже показана архитектура нейронной сети с двумя слоями (обратите внимание, что входной слой обычно не учитывается при расчете количества слоев в нейронной сети).

Создание класса нейронной сети в Python кажется простым делом:

Обучение нейронной сети

Выход i простой двухслойной нейронной сети:

В приведенном выше уравнении веса W и компенсации b являются единственными переменными, которые влияют на выход ί.

Конечно, правильные значения весов и смещений имеют решающее значение для точности прогнозов. Процесс уточнения весов и смещений на основе входных данных называется обучением нейронной сети.

Каждая итерация процесса обучения состоит из следующих шагов.

• вычисление прогнозируемого выхода ŷ, называемого прямым распространением
• обновление весов и смещений, называемых обратным распространением

Следующая диаграмма иллюстрирует этот процесс:

Прямое распространение

Как мы видели на диаграмме выше, прямое распространение — это простое вычисление, и для простой нейронной сети с двумя слоями выход нейронной сети задается формулой:

Для этого добавим в код Python функцию прямого распространения. Для простоты мы предположили, что смещения равны 0.

Однако нам нужен способ оценить «соответствие» наших предсказаний (т.е. насколько далеки друг от друга наши предсказания). С помощью функции потерь мы можем сделать именно это.

Функция потери

Существует множество функций потерь, и характер нашей проблемы должен диктовать выбор функции потерь. В данной работе в качестве функции потерь используется сумма квадратов ошибок.

Сумма квадратов ошибок — это среднее значение разницы между каждым прогнозируемым значением и фактическим значением.

Цель обучения — найти набор весов и компенсаций, который минимизирует функцию потерь.

Обратное распространение

Теперь, когда мы измерили ошибку нашего прогноза (убыток), нам нужно найти способ передать ошибку обратно и обновить наши веса и хеджи.

Чтобы узнать соответствующую величину корректировки весов и смещений, нам необходимо знать производную функции потерь относительно весов и смещений.

Вспомните из анализа, что производная функции — это тангенс наклона функции.

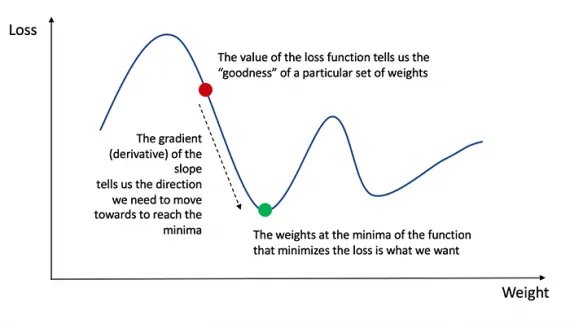
Получив производную, мы можем просто обновить веса и смещения, увеличив/уменьшив их (см. схему выше). Это называется градиентным спуском.

Однако мы не можем напрямую вычислить производную функции потерь после весов и смещений, поскольку уравнение функции потерь не содержит весов и смещений. Поэтому нам необходимо правило цепочки, которое поможет нам в расчетах.

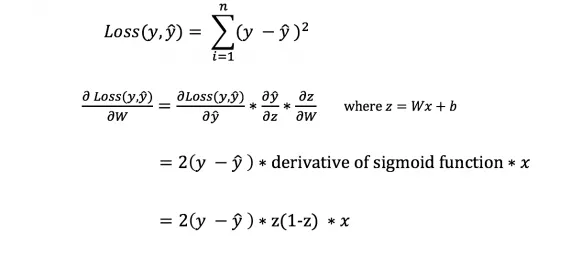
Проверка работы нейросети

Теперь, когда у нас есть полный код Python для прямого и обратного умножения, давайте рассмотрим нашу нейронную сеть в качестве примера и посмотрим, как она работает.

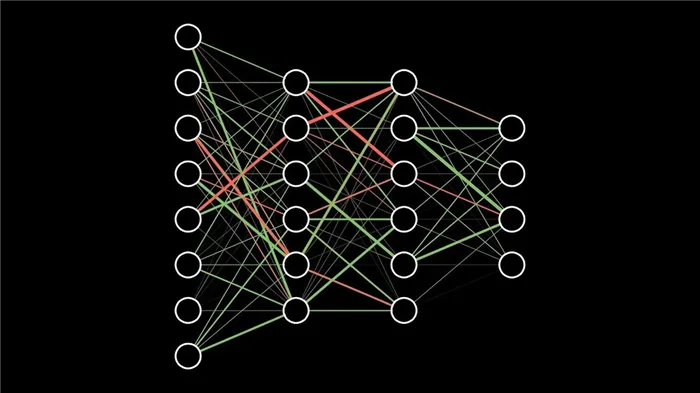
Наша нейронная сеть должна выучить идеальный набор весов для представления этой функции.

Давайте обучим нейронную сеть на 1500 итераций и посмотрим, что получится. Глядя на график потерь за итерацию ниже, мы ясно видим, что потери монотонно уменьшаются до минимума. Это соответствует алгоритму градуированного спуска, рассмотренному ранее.

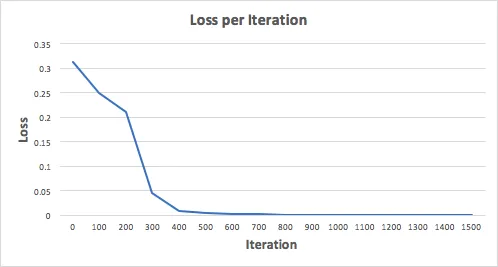
Давайте посмотрим на окончательный прогноз (выход) нейронной сети после 1500 итераций.

Мы сделали это! Алгоритмы прямого и обратного распространения показали успешную работу нейронной сети, и прогнозы сходятся с фактическими значениями.

Следует отметить, что существует небольшая разница между прогнозами и фактическими значениями. Это желательно, так как позволяет избежать переобучения и лучше обобщить нейронную сеть на невидимые данные.

Финальные размышления

Я многому научился, написав собственную нейронную сеть с нуля. Хотя библиотеки глубокого обучения, такие как TensorFlow и Keras, позволяют создавать глубокие сети, не требуя полного понимания внутренней работы нейронной сети, я считаю полезным для начинающих Data Scientists развивать более глубокое их понимание.

Я вложил много личного времени в этот проект и надеюсь, что вы найдете его полезным!

Формула для вычисления выхода нейронной сети

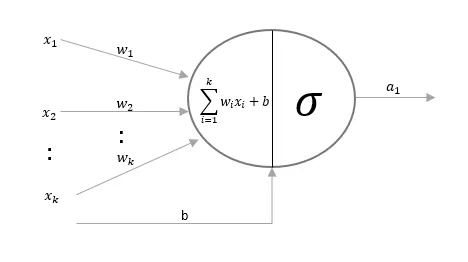
Итак, по какой формуле вычисляется выходное значение нейрона? Сначала мы формируем взвешенную сумму входных сигналов:

Затем мы нормализуем это выражение так, чтобы результат был между 0 и 1. Для этого в данном примере я использую математическую функцию под названием сигмоид:

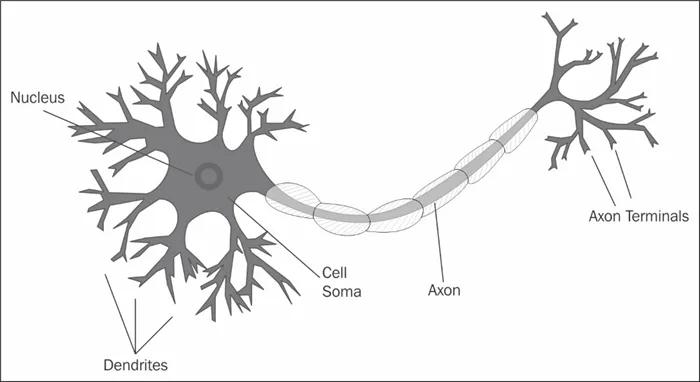
Если построить график этой функции, то он будет выглядеть как S-образная кривая (рис. 4).

Подставив первое уравнение во второе, мы получим окончательную формулу для выхода нейрона.

Вы заметите, что для простоты мы не ограничиваем входные данные, так как предполагаем, что входной сигнал всегда достаточен для того, чтобы наш нейрон произвел свой выход.

Машинное обучение и нейронные сети

Ряд продвинутых курсов для изучения машинного обучения и глубокого обучения, от классических моделей до нейронных сетей. Дополнительная скидка 5% с кодом купона BLOG.

Формула корректировки весов

Во время цикла обучения (см. рис. 3) мы постоянно корректируем веса. Но на сколько? Для расчета используется следующая формула:

Давайте разберемся, почему формула выглядит именно так. Сначала нужно учесть, что мы хотим скорректировать веса в зависимости от величины ошибки. Затем ошибка умножается на значение, поданное на вход нейрона, которое в нашем случае равно 0 или 1. Если на вход подается 0, вес не корректируется. И, наконец, выражение умножается на наклон сигмоиды. Давайте разберемся с последним шагом по порядку:

1. Мы использовали сигмоиду для того, чтобы посчитать выход нейрона.
2. Если на выходе мы получаем большое положительное или отрицательное число, то это значит, что нейрон был весьма уверен в том или ином решении.
3. На рисунке 4 мы можем увидеть, что при больших значениях переменной градиент принимает маленькие значения.
4. Если нейрон уверен в том, что заданный вес верен, то мы не хотим сильно корректировать его. Умножение на градиент сигмоиды позволяет добиться такого эффекта.

Сигмоидальный наклон может быть рассчитан по следующей формуле:

Таким образом, подставив второе уравнение в первое, мы получим следующую формулу для корректировки веса.

Существуют и другие формулы, позволяющие нейрону обучаться быстрее, но преимущество этой формулы в том, что ее довольно легко понять.

Как написать это на Python

Хотя мы не будем использовать какие-либо специальные библиотеки для нейронных сетей, мы представим следующие 4 метода из математической библиотеки numpy:

• exp — функция экспоненты
• array — метод создания матриц
• dot — метод перемножения матриц
• random — метод, подающий на выход случайное число

Например, теперь мы можем представить наше обучающее множество с помощью array():

training_set_inputs = array(0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)= training_set_outputs = array(0, 1, 1, 1, 1, 0).T

Функция .T перемещает массив из горизонтального положения в вертикальное. Следовательно, компьютер хранит эти числа именно таким образом:

Теперь мы готовы к более элегантной версии кода. Наконец, добавим несколько замечаний.

Обратите внимание, что на каждой итерации мы обрабатываем все обучающее множество одновременно. Таким образом, все наши переменные — это массивы.

Итак, вот полностью функциональный пример нейронной сети, написанный на Python:

из numpy import exp, array, random, dot

class NeuralNetwork(): def __init__(self): мы устанавливаем элемент создания для генератора случайных чисел, чтобы он производил одинаковые числа при каждом запуске random.seed(1)

Мы моделируем простой нейрон с тремя входными соединениями и одним выходом. Мы присваиваем случайные веса матрице 3 x 1, где веса варьируются о т-1 до 1, а среднее значение равно 0. self.synaptic_weights = 2 * random.random((3, 1))) — 1

Сигмоидная функция, график которой имеет форму буквы S. Мы используем эту функцию для нормализации взвешенной суммы входных сигналов. def __sigmoid(self, x): return 1 / (1 + exp(-x))

Производная сигмоидной функции. Это наклон кривой. Его значение показывает, насколько нейронная сеть уверена в настоящем весе. def __sigmoid_derivative(self, x): return x * (1 — x).

Мы обучаем нейронную сеть методом проб и ошибок, каждый раз корректируя веса синапсов. def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations): for iteration in xrange(number_of_training_iterations): Обучающий набор передается нейронной сети (в нашем случае нейрону). output = self.think(training_set_inputs)

Вычислите ошибку (разницу между желаемым выходом и выходом, предсказанным нейроном). ошибка = training_set_outputs — output

Умножьте ошибку на входной сигнал и на наклон сигмоиды. Это дает эффект большей коррекции весов, в которых нейрон не уверен. Нулевые входы не изменят веса. adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output)).

Корректировка весов. self.synaptic_weights += adjustment

Заставьте наш нейрон думать. def think(self, inputs): Маршрутизация входов через нейрон. return self.__sigmoid(dot(inputs, self.synaptic_weights))

Градиентный спуск

Градиентный спуск — это итерационный метод оптимизации, который может найти минимум в виде функции. Он используется, когда нахождение оптимальных значений параметров функции алгебраически сложно.

Интуиция: Представьте себе человека, стоящего на скале в долине. Человек хочет добраться до дна долины, но не знает, в каком направлении спускаться. Он делает шаг и выбирает следующую позицию, основываясь на своем текущем положении. Если он сделал шаг вниз, он продолжит движение в том же направлении, в противном случае он изменит направление. Он делает большие шаги, когда склон долины крутой, а когда он достигает дна долины, он делает меньшие шаги. Наконец, он останавливается, когда достигает дна долины.

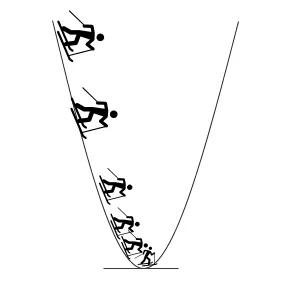
Наша цель — найти оптимальные значения весов и перемещений, при которых функция стоимости минимальна. Алгоритм градиентного спуска включает следующие шаги.

1. Назначьте случайные значения для весов w и смещений b и постоянное значение для скорости обучения
2. Обновите веса и смещения, используя градиент (мы рассчитали с использованием частных производных) и скорость обучения.

Повторяйте шаг 2, пока не найдете минимальное значение или не достигнете максимального количества итераций.

Резюме обучения

Давайте подытожим весь процесс обучения, написав псевдокод для сети с 1 входным, 1 скрытым и 1 выходным слоем.

initialize_weights_and_biases(): output_w = initialize_random_w output_b = initialize_random_b hidden_w = initialize_random_w hidden_b = initialize_random_b train(x_train, y_train, no_of_iterations, learning_rate): # 1. инициализируем веса и смещения сети initialize_weights_and_biases() for iteration in range(no_of_iterations): #выполняем алгоритм градиентного спуска no_of_iterations times #инициализируем дельты весов и смещений wo_delta = initialize_random_w_delta bo_delta = initialize_random_b_delta wh_delta = initialize_random_w_delta wh_delta = initialize_random_b_delta for x, y in zip (x_train, x_train): #Повторите каждый образец в обучающих данных. 2. прямое распространение z_h = hidden_w * x + hidden_b a_h = sigmoid(z_h ) z_o = output_w * a + output_b predicted = sigmoid(z_o) # 3. найти ошибку delta = (predicted - y) # 4. Обратное распространение ошибки delta = 2 error * sigmoid_prime(z_o) wo__delta+= delta * a_h bo_delta+= delta wh_delta+= delta * output_w * sigmoid_prime(z_h) * x bh_delta+= delta * output_w * sigmoid_prime(z_h) # 5. после 1 прохода всех входов обновить веса сети output_w = output_w - скорость обучения * wo_delta output_b = output_b - скорость обучения * bo_delta hidden_w = hidden_w - скорость обучения * wh_delta hidden_b = hidden_b - скорость обучения * bh_delta

Прогноз

После обучения нейронной сети мы получаем оптимальные веса и компенсации для каждого уровня. Прогнозирование — это не что иное, как выполнение прохода прямого распространения на тестовых данных.

Хватит теории, давайте замажем руки и напишем программу на Python для создания глубокой нейронной сети. Мы используем набор данных mnist и создаем сеть, распознающую рукописные цифры, программой Hello World Deep Neural Network.

Мнестические данные состоят из отсканированных рукописных изображений размером 28 x 28 пикселей.

Мы снова создадим сеть с 1 входным слоем, 1 скрытым слоем и 1 выходным слоем.

Следующая программа представляет собой версию описанного выше псевдокода на языке Python. Единственное отличие заключается в том, что мы ввели пакетную обработку, поскольку данные Mnist содержат 60000 строк данных. Если все 60000 строк будут загружаться в память на каждой итерации, память будет повреждена.

def sigmoid(z): return 1.0/(1.0 + np.exp(-z)) def sigmoid_prime(z): return sigmoid(z)*(1-sigmoid(z)) def vectorized_result(j): e = np.zeros((10, 1)) ej = 1.0 return e class NeuralNetwork: def __init__(self, layers) self.h_biases = np. random.randn(layers1,1) self.o_biases = np.random.randn(layers2,1) self.h_weights = np.random.randn(layers1,layers0) self.o_weights = np.random.randn(layers2,layers1) def forward_propagation(self, x): a = sigmoid(np. dot(self. h_weights, x) + self.h_biases) output = sigmoid(np.dot(self.o_weights, a) + self.o_biases) return output def update_mini_batch(self, batch, l_rate): o_b = np.zeros(self.o_biases.shape) h_b = np.zeros(self.h_biases.shape) o_w = np. zeros(self. o_weights.shape) h_w = np.zeros(self.h_weights.shape) for x, y in batch: o_del_b, h_del_b, o_del_w, h_del_w = self. backprop(x,y) o_b = o_b + o_del_b h_b = h_b + h_del_b o_w = o_w + o_del_w h_w = h_w + h_del_w self.o_weights = self. o_weights - (l_rate/len(batch))*o_w self.h_weights = self.h_weights - (l_rate/len(batch))*h_w self.o_biases = self.o_biases - (l_rate/len(batch))*o_b self.h_biases = self.h_biases - (l_rate/len(batch))*h_b def backprop(self, x, y): z_h = np. dot(self.h_weights, x) + self.h_biases a_h = sigmoid(z_h) z_o = np.dot(self.o_weights, a_h) + self. o_biases predicted = sigmoid(z_o) delta = (predicted - y) * sigmoid_prime(z_o) o_del_b = delta o_del_w = np.dot(delta, a_h. transpose()) delta = np.dot(self.o_weights.transpose(), delta) * sigmoid_prime(z_h) h_del_b = delta h_del_w = np.dot(delta, x. transpose()) return (o_del_b, h_del_b, o_del_w, h_del_w) def fit(self, train_data, epochs, mini_batch_size, learning_rate): n = len(train_data) for i in range(epochs): random. shuffle(train_data) batches = train_dataj:j+mini_batch_size for j in range(0,n, mini_batch_size) for batch in batches: self.update_mini_batch(batch, learning_rate) print("epoch<>completed".format(i)) def accuracy(self, test_data): test_results = (np.argmax(self.forward_propagation(x)), y) for (x, y) in test_data return sum(int(x == y) for (x, y) in test_results)

Функция __init__ произвольно инициализирует веса и смещения для выходного и скрытого слоев.

forward_propagation выполняет прямое распространение для заданного входа

update_mini_batch выполняет прямое и обратное распространение для каждой записи в данной партии. Мы используем дельта-суммирование ошибок, потому что мы используем сумму квадратов ошибок, а частная производная — это сумма наклона ошибок всех образцов.

Дата-сет

Набор данных — это набор данных, которые необходимо проанализировать. В нашем случае это текстовый файл со строками в формате вопрос/ответ.

Все текстовые строки ищутся с помощью функции for путем удаления из текста всех ненужных символов с помощью маски, расположенной в переменной alphabet. Каждое строковое значение хранится отдельно в таблице набора данных.

После обработки текста все значения преобразуются в векторы с помощью библиотеки машинного обучения Scikit-learn. В данном примере используется функция CountVectorizer(). Затем все векторы относят к классу с помощью классификатора LogisticRegression().

Когда от пользователя приходит сообщение, оно также преобразуется в вектор, а затем нейронная сеть пытается найти в наборе данных похожий вектор, соответствующий вопросу, и если такой вектор найден, мы получаем ответ.

Голосовой ассистент

Библиотека SpeechRecognition используется для распознавания голоса робота и его ответов. Система ждет в бесконечном цикле вопроса, в нашем случае голоса из микрофона, затем преобразует его в текст и отправляет в нейронную сеть для обработки. После получения текстового ответа он преобразуется в речь, запись сохраняется в папке проекта и удаляется после воспроизведения. Это так просто! Для простоты все сообщения воспроизводятся в текстовом виде на консоли.

При настройках по умолчанию время отклика было довольно долгим, иногда приходилось ждать 15-30 секунд. Кроме того, вопрос был принят с наименьшим количеством шума. Следующие настройки были полезны:

voice_recognizer.dynamic_energy_threshold = False voice_recognizer.energy_threshold = 1000 voice_recognizer.pause_threshold = 0.5

И timeout = None, phrase_time_limit = 2 в listen()

В результате робот отреагировал с минимальной задержкой.

Вам могут понадобиться другие значения. Описание этих и других настроек можно найти на той же странице PyPI в разделе библиотеки SpeechRecognition, но настройку phrase_time_limit я там почему-то не нашел. Я случайно наткнулся на него в Stack Overflow.

import speech_recognition as sr from gtts import gTTS import playsound import os import random from sklearn.feature_extraction.text import CountVectorizer from sklearn.linear_model import LogisticRegression # Словарь def clean_str(r): r = r. lower() r = c for c in r if c in alphabet return ''. join(r) alphabet = ''1234567890-tsukengshshshzchyfyvaproljayachsbyeqwertyuiopasdfghjklzxcvbnm'' with open('dialogues. txt', encoding='utf-8') as f: content = f.read() blocks = content.split('

‘) dataset = for blocks in blocks: replicas = block. split(‘\\\\’):2 if len(replicas) == 2: pair = clean_str(replicas0), clean_str(replicas1) if pair0 and pair1: dataset. append(pair) X_text = y = for question, answer in dataset:10000: X_text.append(question) y += answer vectorizer = CountVectorizer() X = vectorizer. fit_transform(X_text) clf = LogisticRegression() clf.fit(X, y) def get_generative_replica(text): text_vector = vectorizer.transform(text).toarray()0 question = clf. predict(text_vector)0 return question # голосовой помощник def listen(): voice_recognizer = sr. Recognizer() voice_recognizer.dynamic_energy_threshold = False voice_recognizer.energy_threshold = 1000 voice_recognizer.pause_threshold = 0.5 with sr. Microphone() as source: print(«Говорите 🎤») audio = voice_recognizer. listen(source, timeout = None, phrase_time_limit = 2) try: voice_text = voice_recognizer.recognize_google(audio, language=»ru») print(f «Вы сказали: «) return voice_text except sr. UnknownValueError: return «ошибка распознавания» except sr. RequestError: return «ошибка соединения» def say(text): voice = gTTS(text, lang=»ru») unique_file = «audio_» + str(random.randint(0, 10000)) + «.mp3» voice.save(unique_file) playsound.playsound(unique_file) os. remove(unique_file) print(f «Bot: «) def handle_command(command): command = command. lower() reply = get_generative_replica(command) say(reply) def stop(): say(«Bye») def start(): print(f «Bot start. «) while True: command = listen() handle_command(command) try: start() except KeyboardInterrupt: stop()

Примером одного из самых популярных голосовых помощников является Яндекс Алиса.

Попробуйте сами

Если вам понравилась эта статья, вы можете отблагодарить автора суммой, которую считаете нужной:

• Поэкспериментируйте с количеством нейронов в скрытом слое. Сможете ли вы увеличить точность?
• Попробуйте добавить больше слоев. Тренируется ли сеть от этого медленнее? Понимаете ли вы, почему?
• Попробуйте RandomForestClassifier (нужна библиотека scikit-learn) вместо нейронной сети. Увеличилась ли точность?

Модели глубокого обучения в Keras

Узнайте, что вы можете сделать сами, чтобы погрузиться в мир машинного обучения с помощью Python:

Keras основан на моделях, основным типом которых является последовательность, т.е. линейный стек стеков.

Идея заключается в следующем: Создается последовательность, в которую добавляются слои в том порядке, в котором должны выполняться вычисления. После определения составляется модель, которая использует базовую платформу для оптимизации расчетов.

Затем модель необходимо подогнать под данные — это можно сделать пакетно или выполнить обучение модели целиком. Когда обучение завершено, модель можно использовать для прогнозирования новых данных.

Как установить Keras

Существует также другой тип модели — класс Model, который используется с функциональным API.

Установить его несложно, главное, чтобы был установлен один из двигателей. Я рекомендую вам попробовать TensorFlow. Установка подробно описана на официальном сайте.

• cuDNN – требуется, если необходимо проводить расчеты с использованием GPU;
• HDF5 и h5py – предназначены для сохранения моделей Keras на диск;
• graphviz и pydot – используются утилитами визуализации для построения графов моделей.

Вам также могут понадобиться следующие аксессуары:

После этого вы можете установить Keras, выполнив всего одну команду:

pip install keras

Альтернативной командой является установка из репозитория GitHub. Сначала необходимо создать клон:

git clone https://github.com/keras-team/keras.git

Затем перейдите в папку, в которой находится библиотека, и выполните команду:

Работа с Keras на примере

cd keras sudo python setup.py install

Шаг 1: Используем набор помеченных данных

Давайте рассмотрим, как Keras работает с движком TensorFlow, на примере основных операций: Загрузка набора данных, создание модели, добавление параметров, компиляция, обучение и оценка. Мы будем использовать их для создания собственного классификатора для рукописных цифр на основе набора данных MNIST.

В Keras есть множество наборов данных с метками, которые можно импортировать. В нашем случае нам нужен MNIST, который можно загрузить следующим образом:

Шаг 2: Загружаем необходимые слои

from Keras.datasets import mnist (X_train, y_train), (X_test, y_test) = mnist.load_data().

Keras включает в себя большое количество слоев и параметров: функции потерь, оптимизаторы, метрики оценки и многое другое. Они используются для создания, настройки, обучения и оценки нейронных сетей.

Нам нужны следующие слои:

from keras.models import Sequential from keras.layers import Dense from keras.layers import Dropout from keras.layers import Flatten from keras.optimizers import Adam from keras.utils import np_utils.

Мы также используем сверточную нейронную сеть для классификатора:

Шаг 3: Используем метод предварительной обработки данных

from keras.layers.convolutional import Conv2D from keras.layers.convolutional import MaxPooling2D

Мы используем метод Keras.np_utils.to_categorical() для последовательного кодирования y_train и y_test. Это выглядит следующим образом:

Шаг 4: Используем метод add ()

X_train = X_train.reshape(X_train.shape0, X_train.shape1, X_train.shape2, 1).astype(‘float32’) X_test = X_test.reshape(X_test.shape0, X_test.shape1, X_test.shape2, 1). astype(‘float32’) # нормализуем и получаем данные от 0 до 1 X_train/=255 X_test/=255 number_of_classes = 10 y_train = np_utils.to_categorical(y_train, number_of_classes) y_test = np_utils.to_categorical(y_test, number_of_classes)

Для добавления импортированных слоев мы используем метод add():

Шаг 5: Используем метод compile ()

model = Sequential() model.add(Conv2D(32, (5, 5), input_shape=(X_train.shape1, X_train.shape2, 1), activation=’relu’) model.add(MaxPooling2D(pool_size=(2, 2)) model.add(Conv2D(32, (3, 3), activation=’relu’)) model. add(MaxPooling2D(pool_size=(2, 2)) model.add(Dropout(0.5)) model.add(Flatten()) model.add(Dense(128, activation=’relu’)) model.add(Dropout(0.5)) model.add(Dense(number_of_classes, activation=’softmax’))

Этот метод предназначен для процесса обучения:

Шаг 6: Используем метод fit ()

model.compile(loss=’categorical_crossentropy’, optimizer=Adam(), metrics=’accuracy’)

Давайте потренируемся с помощью метода fit():

model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=5, batch_size=200)

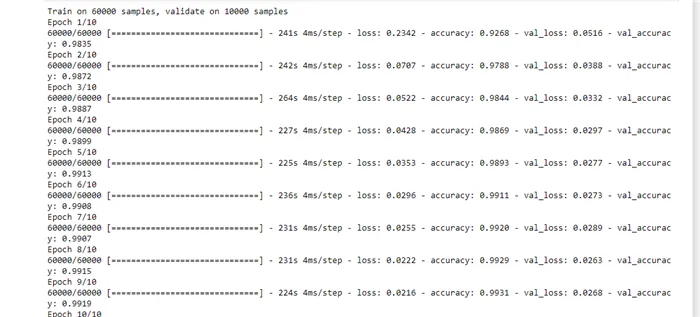
Шаг 7: Оцениваем модель

Обучение проходит следующим образом: